毛细管模型中流体启动流动力学分析及应用

玄建

（胜利油田勘探开发研究院，山东东营257000）

毛细管模型中流体启动流动力学分析及应用

玄建

（胜利油田勘探开发研究院，山东东营257000）

毛细管模型中，根据Poiseuille导管流动公式和牛顿第二定律建立单相流体的启动流动方程，求解得到位移、速度等参数随时间的变化，进而得出了毛细管中单相流体的启动流动过程中惯性力和渗流阻力之间的变化规律。根据毛细管模型中流动，阐述了启动压力梯度问题。

毛细管；启动压力梯度；流体

对砂岩储集岩，常常把微小的孔隙看成毛细管，由于毛细管模型简单，便于分析，因此研究毛细管模型有利于对渗流问题的深入认识。自Hagen-Poiseuille发表了导管流动公式以来，毛细管模型在环境科学、水利工程、石油工业、医学等方面得到了广泛的应用。很多学者做了大量的毛细管模型研究，大部分基于稳定流态，对启动流动的研究较少。在很多实验中，得到了启动压力梯度，这正是测量初始阶段启动流动的反应。很多学者对启动压力梯度持怀疑态度，也给出了合理的解释。本文通过毛细管模型中启动流动的力学研究，进一步阐释了启动压力梯度问题。

1 毛细管模型与达西公式

Hagen-Poiseuille[1]（1842年）发表了导管流动公式，模型假设流体为不可压缩牛顿流体并在管中作层流的条件下，得到了经典的Poiseuille方程式：

Henry Darcy[2]（1856年）研究水在砂滤器中流动时得出了经验达西公式，用以描述流体流经特定形状的多孔介质系统的性质。

在毛细管中的流体流动既遵循Poiseuille公式，也遵循达西公式，Kozeny公式给出了两个公式之间的关系式。

2 毛细管中启动流动方程的建立

假设在较长毛细管中有长为L的流体，在其两端施加Δp压力差，由静止开始运动。在运动过程中，Δp既要克服渗流阻力使流体运动，又要使流体做加速运动。克服渗流阻力使流体运动符合Poiseuille公式，使流体做加速运动符合牛顿第二运动定律。

根据位移、速度、加速度的关系可以得到：

初始条件为：当t=0时，s=0，s'=0，求解得：

进而求得速度v和加速度a：

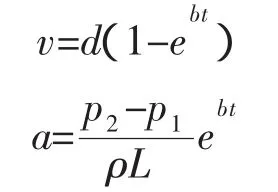
根据牛顿第二运动定律作用在流体上并使其加速运动的压力为：

根据以上计算可以看出当毛细管半径在微米级时，流体在极短时间内加速度消失，损耗在加速上的压力Δp'也随之消失，流体达到了稳定流动状态。

3 启动压力梯度探讨

有的学者通过实验方法提出启动压力梯度是存在的（见图1）[3-10]，有的学者认为不存在，认为启动压力梯度只是一个实验假象[11]。从毛细管理论模型中流体启动流动研究来看，只要压力大于毛管力，毛细管中的流体就会流动，因此启动压力梯度是不存在的。而在实验过程中经常得到一个启动压力梯度，即在压力梯度较小时，渗流规律并不符合Poiseuille公式和达西公式，也与毛细管模型中启动流动公式不一致。

图1 实验室得到的渗流指示曲线示意图

实验中用的岩心可以看成有很多个不等径毛细管组成的毛细管模型，由于在油藏条件下，油相基本上是非润湿相[12，13]。假设该模型中流体为非润湿相，那么毛管力就是流动阻力。由于毛管力的作用，在较低的压力梯度驱替时，大部分毛细管中的流体不流动，只有较大的毛细管中的流体流动。而这部分较大毛细管的横截面积仅占整个岩心横截面积的一部分，随着驱替压力的逐渐增加，参与流动的毛细管越来越多，直至驱替压力能够驱动绝大部分毛细管中的流体。

假设有一岩心由r1、r2（r1＞r2）两种毛细管组成，毛细管中的流体为非润湿相，当压力达到pc1＜pr1＜pc2时，r1毛细管中流体流动，流动符合：

当压力达到pr2＞pc2时，r1、r2毛细管中流体流动，流动符合：

合并得：

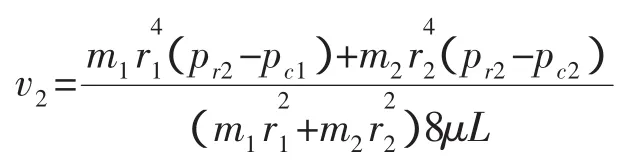
因为r1＞r2，所以，也就是说，pc1＜p1＜pc2时的斜率大于pr2＞pc2时的斜率，而在实验测量时，得到的斜率是逐渐增大的，这是因为实验时采用的速度不是真实速度，而是视速度，即流量除以岩心的横截面积得到，那么斜率就变成了，这样，与实验结果一致。

同理可得，当存在三种半径r1、r2、r3（r1＞r2＞r3）或者更多种毛细管时，视速度V与关系图中，斜率逐渐增大，与实验得出数据一致。

4 结论

（1）从流体在毛细管模型中由静止开始运动过程的理论推导来看，毛细管中的流体在极短的时间内就能达到稳定流态，惯性力在极短的时间内消失，压力只用于克服渗流阻力。

（2）根据理想毛细管模型来看，实验测量的渗流指示曲线中出现的低速渗流曲线段和高速渗流直线段是合理，这是由于岩心中存在不同半径的孔隙具有不同的毛管力导致的。即在较低的压力梯度时，仅克服较大孔道的毛管力使其中的流体流动，随着压力梯度的不断增加，越来越多的更小半径的孔隙中流体参与流动。当绝大部分孔道中的流体流动时，渗流指示曲线呈现直线段。

符号注释：

Q、Q1、、Q2-流量，cm3/s；r、r1、r2、r3-毛细管半径，μm；Δp-毛细管内流体两端压力差，MPa；μ-流体黏度，mPa·s；L-毛细管内流体长度，m；K-岩心渗透率，μm2；A-岩心横截面积，cm2；v、v1、v2-毛细管内流体的速度，m/s；V-流体视速度，m/s；p1、p2、pr1、pr2-压力，MPa；ρ-毛细管内流体的密度，kg/m3；a-毛细管内流体的加速度，m/s2；s-毛细管内流体的位移，m；t-时间，s；b、c、d-常数；Δp'-损耗在流体加速上的压力，MPa；pc1、pc2-毛管力，MPa；m1、m2-半径为r1、r2的毛细管个数。

［1］秦积舜，李爱芬.油层物理学［M］.东营：石油大学出版社，2001：147-149.

［2］杨胜来，魏俊之.油层物理学［M］.北京：石油工业出版社，2004：36-137.

［3］郭平，徐永高，陈召佑，等.对低渗气藏渗流机理实验研究的新认识［J］.天然气工业，2007，27（7）：86-88.

［4］郝斐，程林松，李春兰，等.特低渗透油藏启动压力梯度研究［J］.西南石油学院学报，2006，28（6）：29-32.

［5］吕成远，王建，孙志刚.低渗透砂岩油藏渗流启动压力梯度实验研究［J］.石油勘探与开发，2002，29（2）：86-88.

［6］王道成，李闽，乔国安，等.天然气启动压力梯度实验研究［J］.钻采工艺，2007，30（5）：53-55.

［7］吴凡.气体渗流特征及启动压力规律的研究［J］.天然气工业，2001，21（1）：82-84.

［8］李忠兴.特低渗透油藏启动压力梯度的求解方法及应用［J］.石油勘探与开发，2004，31（3）：107-109.

［9］许建红，程林松，周颖，等.一种求解低渗透油藏启动压力梯度的新方法［J］.石油勘探与开发，2007，34（5）：594-597.

［10］李士伦，孙雷，杜建芬，等.低渗致密气藏、凝析气藏开发难点与对策［J］.新疆石油地质，2004，25（2）：156.

［11］李传亮，杨永全.启动压力其实并不存在［J］.西南石油大学学报，2008，30（3）：167-170.

［12］周惠忠，王利群.两维油藏物理模拟装置［J］.清华大学学报（自然科学版），1994，34（3）：74-82.

［13］杨珂，徐守余.微观剩余油实验方法研究［J］.断块油气田，2009，16（4）：75-77.

The mechanical analysis and application of the flow launch in the capillary tube

XUAN Jian
（Exploration and Development Research Institute of Shengli Oilfield，Dongying Shandong 257000，China）

In the capillary tube,the equation of the single-phase instability flow is established on the basis of the Poiseuille equation and the Newton second law.The change of displacement and velocity with time is obtained.And the relationship of inertia force and seepage flow resistance is calculated.The capillary tube with flow is applied in the analysis of the threshold pressure gradient.

capillary；threshold pressure gradient；flow

TE312

A

1673-5285（2017）02-0077-03

10.3969/j.issn.1673-5285.2017.02.018

2016－12-08

玄建，男（1982-），胜利油田勘探开发研究院工程师，硕士，研究方向为油气田开发，邮箱：xuanjian0202@163.com。