基于MTO边际生产成本受需求波动影响的供应链的协调模型
2017-03-03李忠萍陈彦
李忠萍,陈彦
(1.汕头大学数学系,汕头,515063;2.汕头职业技术学院自然科学部,汕头,515078)
基于MTO边际生产成本受需求波动影响的供应链的协调模型
李忠萍1,陈彦2
(1.汕头大学数学系,汕头,515063;2.汕头职业技术学院自然科学部,汕头,515078)
在商品市场中,需求不仅敏感于价格,同时也会受一些偶然因素而发生波动.在面向订单生产环境下,产品的边际生产成本常常会受需求波动的干扰.本文以单制造商和单零售商组成的二级供应链为研究对象,在面向订单生产环境下,讨论边际生产成本受需求波动干扰的供应链的协调问题.首先,在集中决策和分散决策的情况下,给出了产品的最优零售价格.然后,在集中决策情况下,以供应链的最大利润为目标,提出了合理有效的协调契约,既实现了供应链的最大利润为目标,又确保供应链的成员利润都是Pareto最优.最后,通过数值算例刻画了前文已经取得解析结果.
供应链协调;需求波动;边际生产成本;收益共享契约
0 引言
随着经济全球化和一体化的发展,市场竞争不再是单一企业之间的竞争,更多是供应链之间的竞争[1].然而,由于供应链的成员往往是分散的决策主体,他们以自身利润最大为目标,很容易造成“双重边际效应”,导致供应链绩效水平比较低下.另外,当今市场,需求波动又进一步加剧了供应链绩效恶化的程度.如何有效地促使供应链的成员合作,共同应对需求波动带来的干扰已成为供应链管理研究的核心问题.国内外众多学者认为供应链的协调契约可以提升供应链的绩效水平,并达到完美协调供应链的目的[2-3].因此,不少学者针对需求波动的市场环境,利用契约机制,研究供应链的协调问题.
文献[4]针对单供应商和单零售商组成的两级供应链,考虑市场需求波动下,批发价契约导致“双重边际化效应”,提出了两个等价的契约来引起制造商有组织的制定生产数量实现了供应链协调,有效地减小了需求波动造成的干扰.随后,Zhang等人采用收益贡献协调机制,针对需求受到干扰的情况,分析单制造商和两个竞争零售商组成的两级供应链的协调问题[5].另外,收益共享契约一直以来都是供应链的协调契约的重要形式,针对需求波动,利用收益共享契约协调供应链也被很多学者所研究,且达到了完美的协调目的,文献[7]针对需求受到干扰时,提出一体化双渠道供应链的最优价格及数量决策,并分析了调整价格策略的价值;提出改进的收益共享合约协调突发事件下的分散化双渠道供应链.Zhang等人将文献[5]扩展到两条供应链之间竞争的情况,其中每条供应链由一个风险中性的供应商和一个风险厌恶的零售商组成,研究供应链的成员在面对随机且竞争的需求市场时,采用的最优商业行为(零售价格和批量价格)[8].最近还有一些学者利用其他协调方式来降低需求波动引起的干扰.例如,文献[9]采用期权采购和预售方式降低市场需求的不确定性.
综上所述,研究在需求波动环境下的供应链的协调成果已经非常丰硕.但是,这些研究成果基本上都是针对基于库存生产模式(Make-to-stock,MTS)获得的,而基于订单生产模式(Make-to-order,MTO)下供应链的协调模型文献还是比较少.随着消费水平的提高和市场竞争的加剧,顾客不再满足于接受标准化产品,而倾向于对产品提出自己的个性化要求,进行定制生产,Xiao与Shi等人针对单供应商和单零售商组成的两级供应链,考虑客户关心零售价格与交货时间下,建立了双头垄断市场下的博弈模型来研究供应链与制造商之间的价格与交货时间竞争,发现分散决策下供应链的交货时间增加了,而竞争对方的却减少了,并设计对应的契约来协调MTO模式下供应链[10];Xu等人研究了基于MTO模式下的生产与定价问题[11],但这些作者们并没考虑需求随机波动的影响.而当一些破坏使价格敏感系数和生产成本同时发生变化时,XIE等人研究了怎样协调供应链,结果发现:当破坏满足某个给定的条件,原始的生产计划不需要调整,仅仅需要调节零售价;当破坏超过给定的标准点时,那么生产计划需要调整[12].但XIE等人是基于弹性需求进行研究的.而且,MTO生产模式高个性化需求更加大了市场需求波动性,加上需求市场的一些偶然因素或事件,导致企业的运营管理变得更为艰巨.如何应对MTO生产模式需求波动带来的干扰也显得尤为重要.假设所研究的供应链由单制造商和单零售商组成,边际生产成本也因市场需求波动而受到干扰.那么在这种情况下,供应链作为一个整体应该如何决策商业行为才能实现供应链的利润最大化目标?而当供应链的成员作为独立的决策主体时,作为供应链的领导企业又该如何引导上下游跟随企业做出有利于自身又利于其他成员的决策,同时还能保证供应链的利润最大化的目标?这些都是时下众多MTO生产模式企业面临重大挑战,鉴于此,本文讨论MTO生产模式下需求波动的供应链契约协调模型.
2 符号说明
下面给出本文所涉及的相关变量和参数的定义:
c:需求没有波动情况下的边际生产成本;
p:供应链的零售价格,即零售商向客户收取的产品价格;
ω:制造商向零售商交货的批量价格;
D:单位时间的市场需求量;
a:市场的潜在需求;
b:客户对价格的敏感强度;
ε:需求的随机波动;
c-αε:需求波动ε∈[A,0]时,产品的边际生产成本;
c+βε:需求波动ε∈(0,B]时,产品的边际生产成本;
φ:收益共享协调契约下,制造商分享零售商收益的比例;
Π:整个供应链的单位时间利润;
Πr:零售商的单位时间利润;
Πm:分散决策情况下,制造商单位时间利润.
在后文中,变量下脚标“c”表示集中决策情况,“d”表示分散决策情况,“w”表示批量价格协调契约决策情况,“r”表示收益共享协调契约决策情况,上角标“*”表示最优值或者极大值.
3 主要结论
如图1所示,本文研究单制造商和单零售商组成的二级供应链,信息完全共享,成员完全理性,以MTO模式进行生产.首先,零售商作为供应链与外部需求的接口,以零售价格p接收客户订单,并将客户订单上传给上游的制造商.然后,制造商按照客户要求定制产品,以批量价格ω向零售商交货.本文采用文献[13]的加法需求模型,假设单位时间市场需求率关于价格是单调递减,且受到一定波动的干扰,即
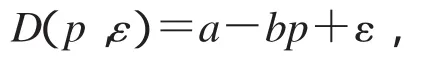
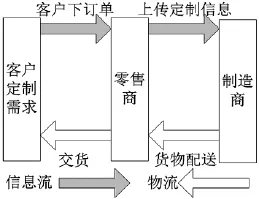
图1 供应链结构
其中ε是[A,B]上的随机变量,其均值为0,方差为δ2,A<0,B>0,其概率密度函数和分布函数分别为f(x)和F(x).
另外,在现实生产中往往会出现这种情况,当需求下降时,由于制造商配置的物力、财力和人力等资源闲置的原因,造成制造商单位产品的生产成本上升.而当需求突然增加时,产品的边际生产成本会变得相对复杂.若制造商的生产能力有限,需求增加只能通过加班赶工,停止本应该进行的机器保养或者员工培训,或者采用外包处理等方式完成,那么需求增加会导致产品的边际生产成本上升.若制造商生产能力柔性比较强,需求增加不仅不会导致边际生产成本上升,还会由于规模经济的原因降低边际生产成本.所以,综上所述,假设如下,当需求波动ε∈[A,0],边际生产成本为c-αε,若α>0故有c-αε>c成立;而当需求波动ε∈(0,B]时,边际生产成本为c+βε,若β>0,则有c+βε>c,说明需求增加会导致边际生产增加,若β<0,则有c+βε<c,说明需求增加会降低边际生产成本.为了方便起见,称β为制造商生产力柔性系数.
3.1 集中决策
首先讨论集中决策的情况,假设供应链中存在一个决策者,掌握了整个制造商和零售商的所有信息,该决策者不以单个企业的利润为目标,而是从全局考虑,以整个供应链的利润最大为目标,做出最优的产品定价,从而实现整个供应链的利润最大化.供应链的单位时间利润为
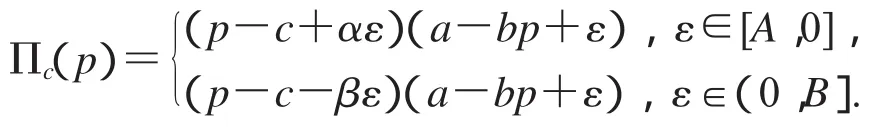
从而,供应链的决策模型为
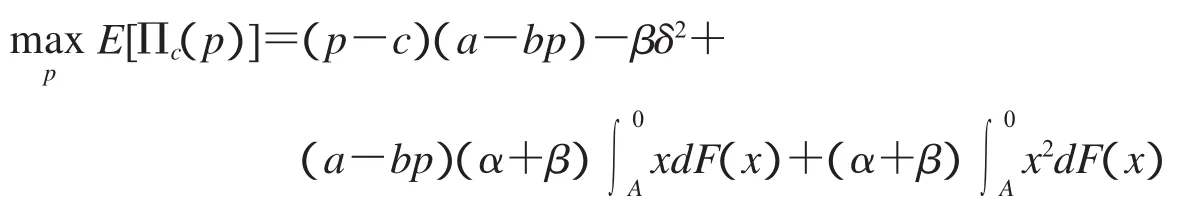
定理3.1在生产成本受需求波动影响的情况下,集中决策模型供应链的单位时间利润是关于零售价格的凹函数,其中最优零售价格为

证明对决策模型(1)的目标函数关于零售价格p求一阶导数和二阶导数,得到

由于b>0,则(4)式小于零,从而推出E[Πc(p)]是关于零售价格p的凹函数,因此存在最优的零售价格使E[Πc(p)]取得最大值.令(3)式等于零,得到最优零售价格
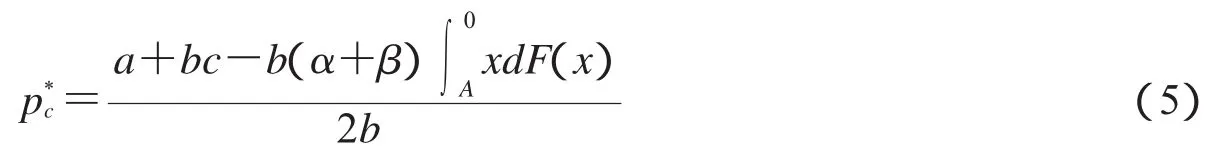
从而定理3.1得证.
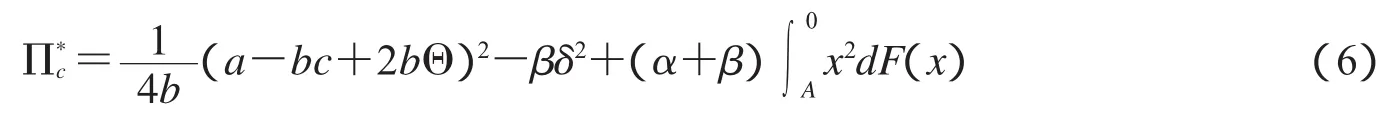
定理3.2在生产成本受需求波动影响和集中决策情况下,最优零售价格分别关于参数a、c、α和β单调递增,而关于参数b单调递减;而且,调价的幅度与客户对价格敏感强度密切相关,客户对价格越敏感,调价幅度越小,反之,调价幅度越大.
证明对最优零售价格(5)分别求参数a,b,c,α和β的一阶偏导,得到

从上面的一阶偏导的正负很容易得到定理3.2的前半部分结论,而,因此,定理3.2得证.
从最优零售价格关于参数a的偏导函数可以发现:当市场潜在需求a增加时,企业会提价来增加企业单位时间利润,相反,当市场潜在需求a减小时,企业会降价来刺激需求,减少企业单位时间利润下降量.最优零售价格关于参数b的偏导函数说明零售价格与客户对价格的敏感强度是方向相反的,当客户对价格越来越敏感时,零售价格应该适当下降,相反,企业可以适当提高零售价格.最优零售价格关于稳定情况下的边际生产成本c的变化情况比较简单,两者的变化方向一致,而且,当c发生变化时,零售价格只需向同方向调动c的变化量的一半即可.从最优零售价格关于α和β的一阶偏导表明零售价格对二者的敏感强度相同,而且与需求波动的分布规律有关.
3.2 分散决策
在分散决策情况下,供应链上两个企业都是理性而自私的,不考虑同一供应链上下游企业的利润情况,都是以各自的利润最大化为目标.接下来采用Stackelberg博弈来分析分散情况下供应链上下游两个企业之间博弈问题.假设制造商是领导者,零售商是跟随者,制造商以批量价格ω向零售商交货,零售商再根据制造商提供批量价格确定最优的零售价格使自身单位时间利润最大化.采用逆序归纳法分析,首先考虑零售商在批量价格ω给定的情况下选择最优的零售价格使其单位时间利润最大化.
3.2.1 零售商的决策模型
零售商单位时间销售利润为

其决策模型为
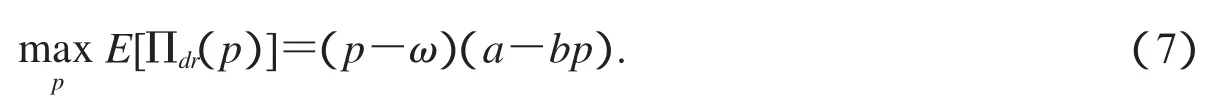
定理3.3在生产成本受需求波动影响和分散决策情况下,制造商作为领导者,零售商作为跟随者,当制造商以批量价格ω向零售商交货时,零售商最优零售价格为

证明对决策模型(7)中的目标函数关于零售价格p求一阶导和二阶导,得到

由于目标函数关于零售价格的二阶导函数小于零,所以零售商单位时间利润是关于零售价格的凹函数.令(9)式等于零,得到在分散决策情况下零售商的最优零售价格为
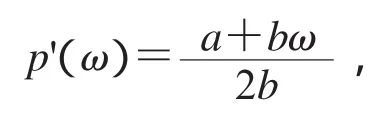
从而证明了定理3.3.
3.2.2 制造商的决策模型
制造商单位时间的利润为

将零售价格表达式(8)代入上述表达式,再对其取期望得到,从而,制造商的决策模型为
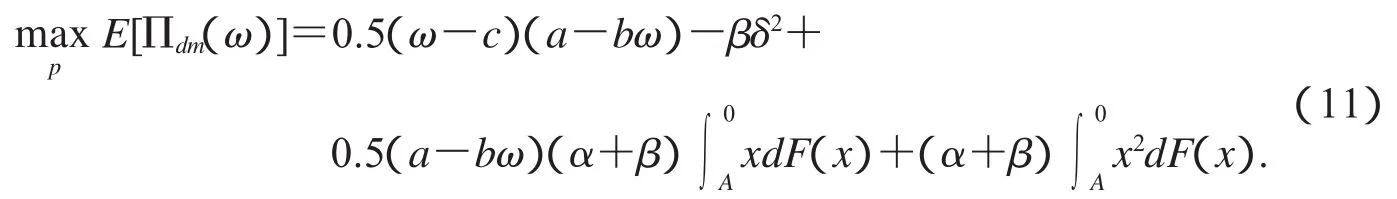
下面以定理的形式给出分散决策情况下制造商最优批量价格的表达式.
定理3.4在生产成本受需求波动影响和分散决策情况下,制造商作为领导者,零售商作为跟随者时,制造商的最优批量价格为

证明对制造商单位时间平均利润表达式(12)关于批发价格w求一阶导和二阶导,得到
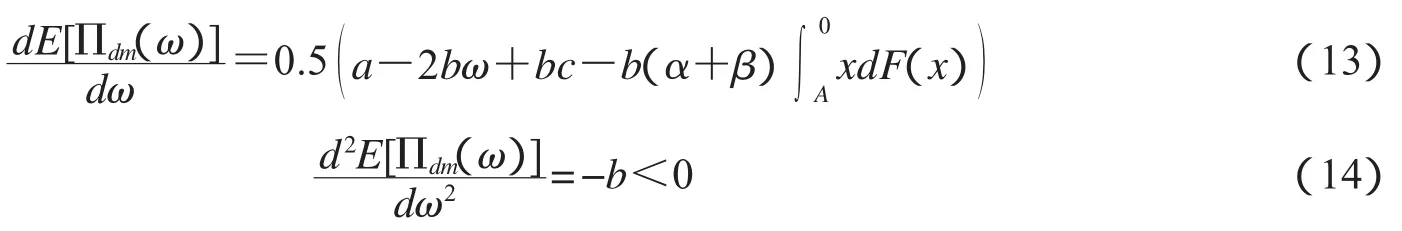
由于d2E[Πdm(ω)]/dω2<0,所以E[Πdm(ω)]是关于批量价格ω的凹函数,故存在最优的ω'使E[Πdm(ω)]最大化,令(13)式等于零,从而得到
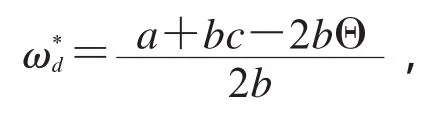
定理得证.
将(12)式代入(8)式得零售商的零售价格为

比较(2)式与(15)式,可以发现:当且仅当a-bc+2bΘ=0时,有成立,然而此时有成立,即零售商以批量价格销售产品能使供应链的单位时间利润达到最大值,但是此时零售单位时间利润为零,显然零售商不会以批量价格销售产品.零售商选择的零售价格必然大于批量价格,从而得到

由于整个供应链的单位时间利润是关于零售价格的凹函数,其中是其最大值点,所以当零售价格为时,供应链的利润必然小于零售价格为时,造成这种现象的原因便是供应链中通常说的“双重边际效应”.
定理3.5与集中决策情况相比,分散决策情况下最优零售价格关于a和b的灵敏性强度比大,而关于c、α和β的灵敏性强度却减弱了.

从定理3.5的结论可以看到,分散决策情况下,外部参数——市场潜在需求a和客户对零售价格的敏感系数b对零售价格的影响比集中决策情况下的影响更大,相反,系统参数——产品的平稳边际生产成本c、α和β对零售价格的影响则减弱了.造成这种结果的原因是在分散决策情况下供应链的“双重边际效应”引起的.在分散决策情况下,供应链的成员更多的是关注于自己利润的变化,零售商最关心的是市场需求的变化,因为市场需求变化是导致零售商利润变化最直接的原因,而对制造商生产成本的关注相对较弱.
将(12)式和(15)式代入(7)式和(11)式得分散决策情况下零售商和制造商单位时间最大利润分别为
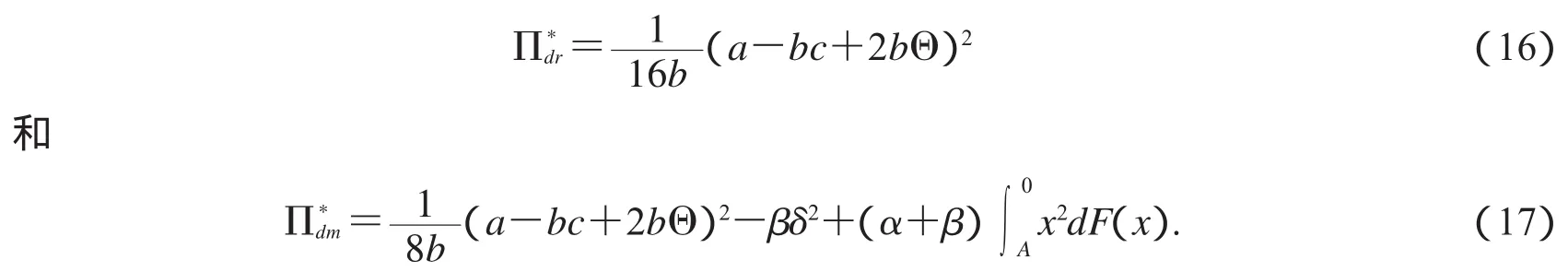
定理3.6生产力柔性系数β,集中决策情况下的供应链整个单位时间最大利润,分散决策情况下零售商单位时间最大利润与分散决策情况下制造商单位时间最大利润
满足以下结论:
Compound 2 amorphous powder; [α]D25 +9.6 (c 0.10, CHCl3); IR (KBr) νmax = 2924, 1719, 1459, 1254, 1055 cm–1; 1H- and 13C NMR (CDCl3), see Table 1; HRESIMS m/z 635.3187 [M + Na]+ (Calcd for C35H48O9Na, 635.3184).

对分散决策情况下,零售商和制造商单位时间最大利润分别关于β求偏导,即
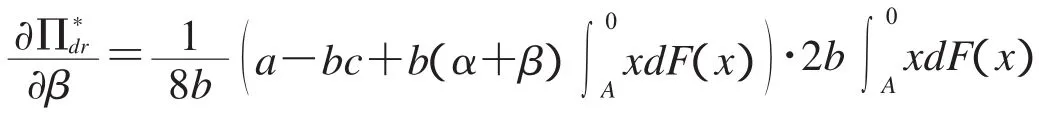
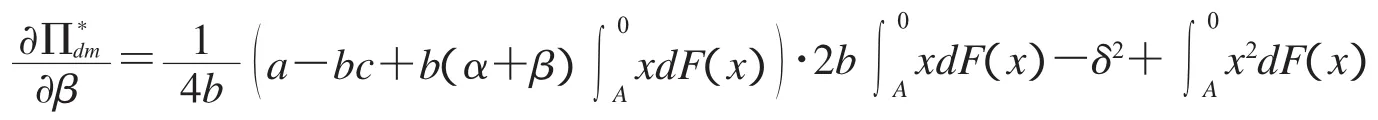
将以上4种情况代入,可发现定理3.6得证.
从定理3.6的结论可以看到,无论是集中决策还是分散决策情况下,生产力柔性系数β越大,供应链成员单位时间最大利润越大,对供应链的效益越有利;同时,分散决策情况下,零售商对生产力柔性系数的反应较制造商敏感,这与实际情况是符合的.
3.3 契约协调
在没有协调机制的情况下,需求波动造成的风险都是由制造商一方承担,所以制造商会尽量抬高产品的批量价格来提高单位产品的剩余利润,从而减小波动风险对自身利润的影响.由于供应链的成员都是理性的,所以成员之间进行合作的前提是彼此获得的利润至少比分散决策情况下大,这是确保供应链的成员单位时间利润在契约协调下都是Pareto改进.在这里主要讨论批量价格协调契约和收益共享协调契约.
首先,看看最简单的协调契约——批量价格协调契约.能否使供应链的单位时间利润最大化,关键就是看契约能否协调零售商以最优零售价格销售产品.所以,根据上文式子(2)和(8),令,从而得到

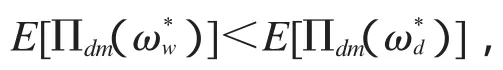
即批量价格契约无法保证制造商的Pareto改进,从而批量价格契约不会被制造商接受.造成这种结果的原因是需求波动造成的风险都是由制造商一方承担,零售商销售单位产品的利润始终都是接下来,采用收益共享契约的形式来协调供应链的成员之间合作,让供应链的成员共同承担需求波动造成的风险.
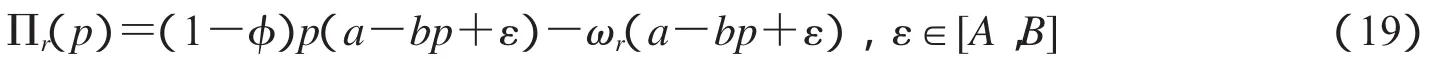
对其取期望,得到
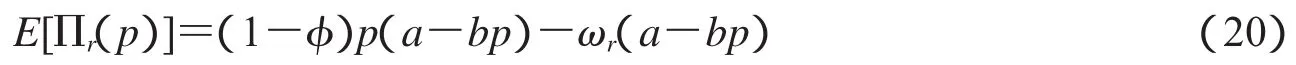
定理3.7在生产成本受需求波动影响的情况下,收益共享协调契约决策模型中,当制造商以批量价格

向零售商交货时,供应链的单位时间利润最大,其中φ是制造商和零售共同协调决定的收益分批比例.
证明:分别对(20)求一阶导和二阶导,得到
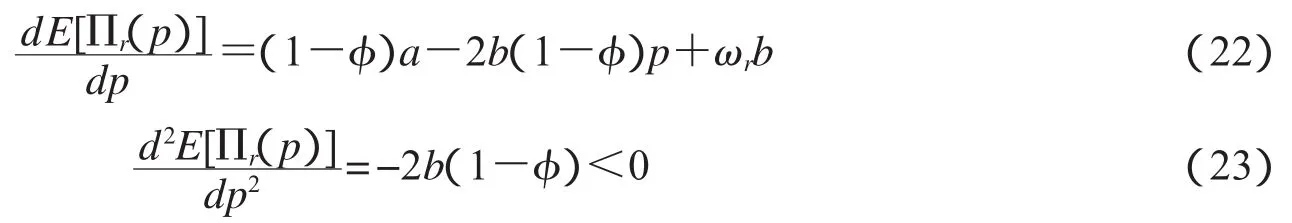
由式(23)可知,E[Πr(p)]是关于零售价格p的凹函数,故存在最优零售价格使E[Πr(p)]取得最大值.令(22)式等于零,可得到最优零售价格为

为了确保供应链的成员单位时间利润在收益共享契约协调下都是Pareto改进,下面讨论收益共享契约参数φ的取值范围.首先,在收益共享契约协调下,制造商和零售商单位时间的平均利润至少比分散决策情况下大,即

联合两个不等式,得到
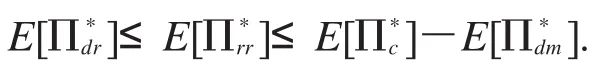
将(21)式和(24)式代入(20)式,得到
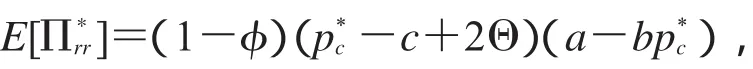
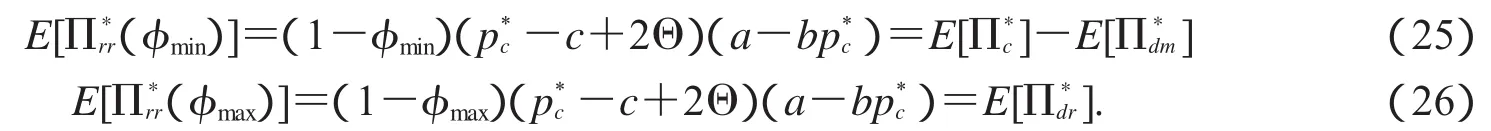
根据上面求得的结果,下面以定理的形式归结供应链的收益共享分配比例.
定理3.8在生产成本受需求波动影响的情况下,收益共享协调契约决策模型中,当批量价格,收益比例φ∈[1/2,3/4]时,供应链的单位时间利润最大,同时也能保证制造商和零售商单位时间利润不小于分散决策情况下的利润.
证明将(6)式和(17)式代入(25)式,得到
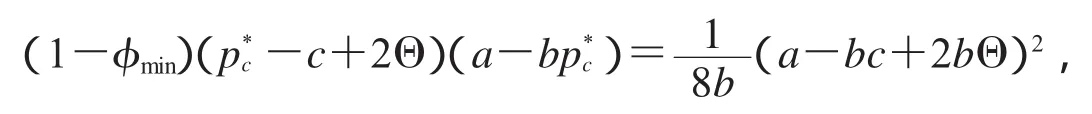
再将(2)式代入上式,从而得到φmin=1/2.同理,将(17)式和代入(26)式,得到φmax=3/4,定理证毕.
收益共享契约最终实施分配比例φ是由制造商和零售商谈判决定的,具体取值看制造商和零售商在供应链中的影响力大小.制造商的影响力越大,最终实施分配比例φ也越大,反之,φ越小.本文考虑的情况是制造商作为领导者,在供应链中占有主导地位,从而制造商占有供应链的利润也偏大.对于零售商作为供应链的领导者的情况可做相似讨论.在收益共享契约协调下,供应链的单位时间利润能达到最大值,同时制造商和零售单位时间利润都满足Pareto改进,说明该契约能够使供应链实现了完美协调.
4 数值分析
接下来,采用数值算例的方式对前文已经取得解析结果做进一步分析,更为直观地描述收益共享契约的协调作用,以及生产成本和需求波动强弱对零售价格和单位时间利润的影响.
假设A公司是一家汽车制造商,和下游的零售商B公司组成一个供应链,以面向订单生产方式按照客户要求进行生产.假设市场日需求量D(p,ε)=10000-0.05p+ε辆/天,其中ε服从正态分布,均值为0,方差为δ2,平稳状态下单位产品生产成本为c=50 000元/辆,α=100元/辆.
首先考虑生产成本对零售价格和单位时间利润的影响,假设需求干扰ε的方差δ2=100,生产力柔性系数β=100(单位:元/辆),生产成本c从50 000变化到100 000(单位:元/辆),制造商和零售商达成的收益分配比例是φ=5/8.
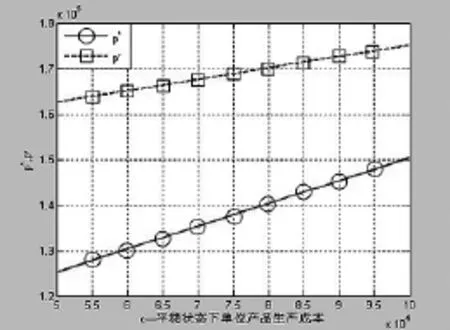
图2 零售价格关于平稳生存成本的变化规律
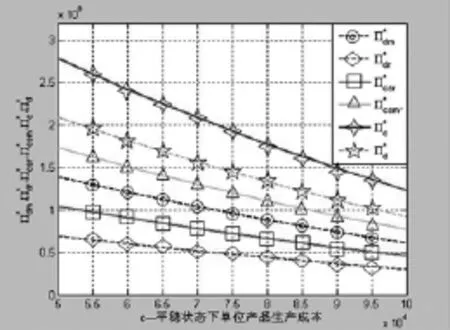
图3 单位时间利润关于平稳生存成本的变化规律
从图2可以看到,随着c的增大,无论是集中决策还是分散决策,零售价格都随之增大.而且,在集中决策环境下,零售价格对c的增加更敏感,随着c的增加增加得更快.这从二者关于c的偏导数可以解释,由于,所以比对c的变化更敏感.造成这种现象的原因是,在集中决策情况下,决策者从全局考虑,当生产成本增加时,为了维持供应链的利润,决策者必然会适当提高产品价格.然而在分散决策情况下,由于产品价格是由零售商决定的,而生产成本却是由制造商承担的,所以当生产成本增加时,首先导致是制造商提高批量价格,然后才是零售商根据提高的批量价格再提高零售价格,而批量价格对生产成本的敏感强度为,零售价格对批量价格敏感强度为,所以在分散决策情况下生产成本的影响是经过制造商才过渡到零售商,零售商对生产成本的增加比集中决策情况下弱,而且相对滞后.
图3刻画了当收益分配比例φ=5/8时,分散情况下和契约协调情况下制造商和零售单位时间利润关于生产成本c的一个趋势,从图像中可见,,说明该契约很好地协调了供应链的成员之间的合作.同时也发现,在该契约的协调下,同时满足,从而保证了制造商和零售单位时间利润都满足Pareto改进的.
接下来讨论生产力柔性系数对集中决策情况下零售价格和供应链的单位时间利润的影响.假设平稳生存成本c=80 000元/辆,生产力柔性系数β从-200变化到100,其他参数与上面的假设相同.
β反应了制造商的柔性强弱,当β<0时表示制造商生产能力具有柔性,β越小,柔性越强.当制造商具有柔性时,需求增加非但不会增加边际生产成本,相反,由于规模经济原因,制造商边际生产成本随着需求的增加而下降.而当β>0时表示制造商制造能力比较刚性,β越大,刚性越强.在这种情况下,需求增加时,只能通过加班赶工,停止本应该进行的机器保养或者员工培训,或者采用外包等方式才能满足客户需求.表1反应了制造商生产能力柔性越来越弱,刚性越来越强时,集中决策情况下,产品价格也是慢慢升高的.相反,由于制造商的柔性越来越差,导致边际生产增加,所以供应链的单位时间利润也随之慢慢下降.说明,柔性制造系统/柔性供应链有利于抵抗需求波动造成的干扰.

表1 生产力柔性系数对集中决策决策情况下零售价格和供应链的单位时间利润的影响
最后分析需求波动强弱对集中决策情况下零售价格和供应链的单位时间利润的影响.假设平稳边际生产成本c=80 000元/辆,生产力柔性系β=100数元/辆,需求波动方差δ2从100变化1 000,其他参数与上面的假设相同.
表2给出的需求波动方差δ2从左到右是越来越大,说明需求波动越来越强.从表2的数据可以看到,集中决策下,产品价格是随波动强度增加而增加的,单位时间利润却是随需求的波动而下降.当需求波动增大时,边际生产成本也随之增大,单位产品剩余利润下降,企业为了维持自身利益,必然会相应的提高零售价格,尽可能地减小利润下降趋势.

表2 需求波动强弱对集中决策决策情况下零售价格和供应链的单位时间利润的影响
5 结论
需求波动是不可避免的,MTO高个性化需求更加大了市场需求波动.如何合理有效协调供应链的成员共同分担需求波动带来的风险,实现供应链的利润最大化已成为当下研究的热点问题.本文以单制造商和单零售商组成的二级供应链为研究对象,讨论MTO边际生产成本受需求波动干扰的供应链的协调问题.
首先,讨论了集中决策和分散决策情况下的最优零售价格.研究发现,在分散决策情况下,由于“双重边际效应”的原因,零售商过分关注市场参数变化,而轻视了系统参数的变化,导致供应链营销策略达不到最优,供应链的利润也没法实现最大化.然后,讨论了批量价格协调机制,发现此机制下制造商利润严重受损,无法实现协调的目的.最后,发现收益共享机制能够很好地协调供应链的成员合作,既实现了供应链的最大利润为目标,又确保供应链的成员利润都是Pareto最优.
另外,本文也给出了诸多可操控的管理启示.最优零售价格关于潜在需求的灵敏强度与自身无关,而与客户对价格的敏感系数呈负相关.当潜在需求发生单位变化时,可沿相同方向调整客户对价格的敏感系数的0.5倍.最优零售价格关于客户对价格的敏感系数的敏感强度即与自身相关,又与潜在需求相关.当边际生产成本发生变化时,只需沿相同方向对零售价格调整生产成本的一半即可.在收益共享协调机制下,制造商作为领导企业时,制造商分享零售的收益比例必须在区间[0.5,0.75]时,供应链才能得到协调,供应链的成员利润也能保证Pareto最优.而且,当制造商分享零售的收益比例越高时,制造商提供给零售商的批量价格也越低,并且两者的变化比例相同.
[1]林强,叶飞,陈晓明.随机弹性需求条件下基于CVaR与收益共享契约的供应链决策模型[J].系统工程理论与实践,2011,31(12):2296-2307.
[2]李新然,牟宗玉.需求扰动下闭环供应链的收益费用共享契约研究[J].中国管理科学,2013,21(6):88-96.
[3]BECKER-PETHM,THONEMANN U W.Reference points in revenue sharing contracts-How to design optimal supply chain contracts[J].European Journal ofOperational Research,2016,249(3):1033-1049.
[4]LI X,LI Y J,CAIX Q.Double marginalization and coordination in the supply chain with uncertain supply [J].European Journal ofOperational Research,2013,226(2):228-326.
[5]ZHANG W G,FU J H,LI H Y,et al.Coordination of supply chain with a revenue-sharing contract under demand disruptions when retailers compete[J].International Journal of Production Economics,2012,138(1):68-75.
[6]于辉,陈剑.需求依赖于价格的供应链应对突发事件[J].系统工程理论与实践,2007(3):36-41.
[7]曹二保,郑健哲,马玉洁,等.双渠道供应链应对需求扰动的协调机制研究[J].管理科学学报,2014,11(2):267-273.
[8]XIAO T J,YANG D Q.Price and service competition of supply chain with risk-averse retailers under demand uncertainty[J].International Journal ofProduction Economics,2008,114(1):187-200.
[9]慕银平,冯毅,唐小我.随机需求下期权采购与预售联合决策研究[J].管理科学学报,2011,14(6):47-56.
[10]XIAO T,SHI J,CHEN G.Price and leadtime competition,and coordination for make-to-order supply chains[J].Computers&Industrial Engineering,2014,68:23-34.
[11]XU X P,ZHANG W,HE P,et al.Production and pricing problems in make-to-order supply chain with cap-and-trade regulation[J].Omega,2015,in press.
[12]XIE D C,CHEN H,WEI L.Howto coordinate integrated supply chain when demand and cost disruptions occur simultaneously[J].Management Science and Engineering,2015,9(1):14-18.
[13]PETRUZZI N C,DADA M.Pricing and the newsvendor problem:a review with extensions[J].Operation research,1999,47(2):183-194.
Coordination of a MTO Supply Chain with Marginal Production Costs Influenced by Demand Disruption
LI Zhongping1,CHEN Yan2
(1.Department of Mathematics,Shantou University,Shantou 515063,Guangdong,China; 2.Department of Natural Sciences,Shantou Polytechnic,Shantou 515078,Guangdong,China)
In the commodity market,demands not only are sensitive to price,but also are disrupted by some haphazard factors,such as the financial crisis,the new tax policy,the promotion of substitutable products,and so on.In the make-to-order setting,marginal production costs usually are imposed considerable deviation due to demand disruption.In this paper,the coordination of a make-to-order supply chain is discussed where marginal production costs are imposed deviation due to demand disruption.At first,the optimal retail prices for the centralized supply chain and the decentralized one,respectively.Then,setting the maximum profit of centralized supply chain as the target,a reasonable and effective coordination contract is proposed which can achieve the target and realize Pareto optimization for the profits of the supply chain members,simultaneously.At last,the analytic results which have been obtained above are described by a numerical study.
supply chain coordination;demand disruption;marginal production costs;revenue sharing contract
C934
A
1001-4217(2017)01-0063-13
2015-12-02
李忠萍(1989—),女,安徽人,研究生,研究方向:最优化理论与方法.E-mail:amandalizp@outlook.com
陈彦(1962—),男,广东人,副教授,研究方向:随机模型理论与方法.E-mail:13643031811@126.com.
