赏析中考之“双统计图”

杨美华

赏析中考之“双统计图”

杨美华

中考会常常围绕课本，借助变式，设计出许多题材新颖、形式丰富、难度适中的双统计图试题，旨在考查同学们的读图、析图的能力.统计图是一种最直观的交流语言，接下来让我们一起欣赏2016年中考题里的“双统计图”吧！

一、扇形与条形统计图组合

例1（2016·甘肃白银）2016年《政府工作报告》中提出了十大新词汇.为了解同学们对新词汇的关注度，某数学兴趣小组选取其中的A：“互联网+政务服务”、B“工匠精神”、C“光网城市”、D“大众旅游时代”四个热词，在全校学生中进行了抽样调查，要求被调查的每位同学只能从中选择一个自己最关注的热词.根据调查结果，该小组绘制了如图1和图2两幅不完整的统计图.请你根据统计图提供的信息，解答问题：（1）本次调查中，一共调查了多少名同学？（2）条形统计图中，m=_____，n=_____；（3）扇形统计图中，热词B所在扇形的圆心角是多少度？

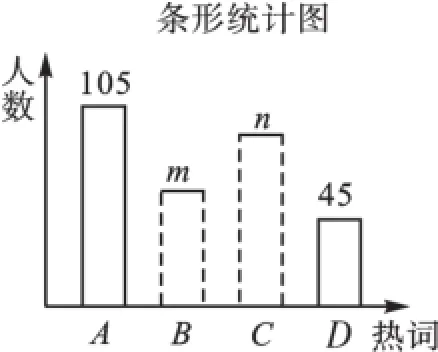
图1

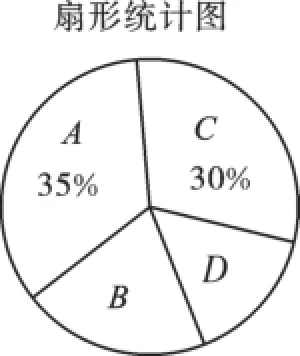
图2

【解析】（1）结合条形统计图中最关注热词A的具体人数和扇形统计图中最关注热词A的人数所占的百分比可求出被调查的学生总数：105÷35%=300（人），即共调查了300名学生；（2）从扇形统计图中最关注热词C的人数所占的百分比和被调查的学生总数可求出最关注热词C的具体人数n，用总人数分别减去最关注热词A、热词C和热词D的人数就可以得到m值：n=300×30%=90（人），m=300-105-90-45=60（人）；（3）由最关注热词B的人数所占的百分比乘360°即可，，即B所在扇形的圆心角是72°.

二、扇形与折线统计图组合

例2（2016·四川绵阳）绵阳七一中学开通了空中教育互联网在线学习平台，为了解学生使用情况，该校学生会把该平台使用情况分A（经常使用）、B（偶尔使用）、C（不使用）三种类型，并设计了调查问卷，先后对该校初一（1）班和初一（2）班全体同学进行了问卷调查，并根据调查结果绘制成如下两幅不完整的统计图，请根据图中信息解答问题：（1）求此次被调查的学生总人数；（2）求扇形统计图中代表类型C的扇形的圆心角，并补全折线统计图；（3）若该校初一年级学生共有1000人，试根据此次调查结果估计该校初一年级中C类型学生约有多少人.

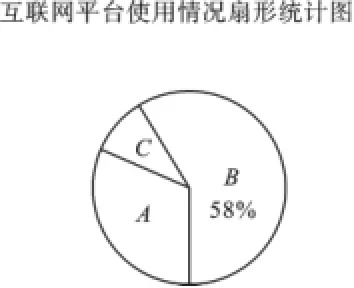
图3

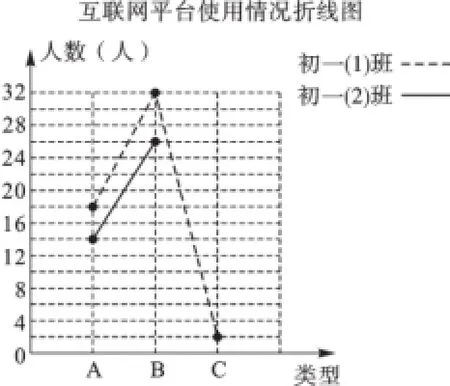
图4

【解析】（1）由扇形统计图知类型B人数所占比例为58%，从折线统计图知类型B人数＝26＋32＝58（人），所以此次被调查的学生总数＝58÷58%＝100（人）.（2）由折线图知类型A人数＝18＋14＝32（人），故类型A学生的比例＝32÷100＝32%，所以类型C学生所占的比例＝1-32%-58%＝10%，所以扇形统计图中代表类型C学生的扇形圆心角＝360°×10%＝36°，初一（2）班类型C学生人数＝10%×100-2＝8（人），补全折线统计图如图5所示.（3）根据此次抽样调查可知类型C学生的比例占样本总数的10%，以此估计该校初一全年级类型C学生约有1000×10%＝100（人）.

图5

三、条形与折线统计图组合

例3（2016·山东济宁）2016年6月15日是父亲节，某商店老板统计了近四年父亲节当天剃须刀的销售情况，以下是根据该商店剃须刀销售的相关数据所绘制的统计图的一部分.

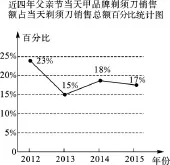
图6

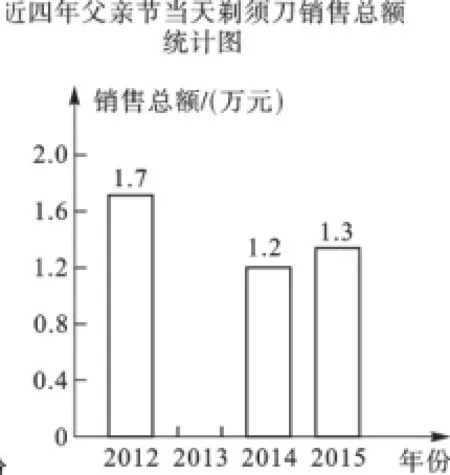
图7

根据图6、图7解答下列问题：（1）近四年父亲节当天剃须刀销售总额一共是5.8万元，请将图7中的统计图补充完整；（2）计算该店2015年父亲节当天甲品牌剃须刀的销售额.

【解析】（1）将四年销售总额减去2012、2014、2015年的销售总额，求出2013年的销售额即可，5.8-1.7-1.2-1.3=1.6（万元），补全条形统计图如图8所示：

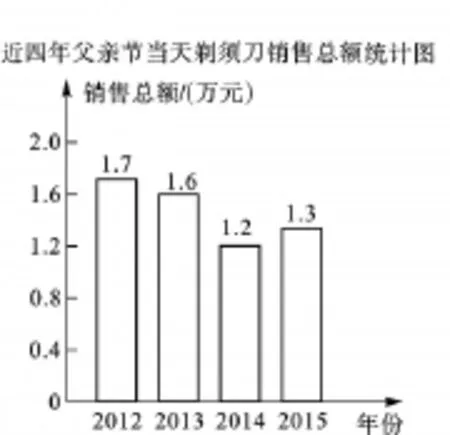
图8

（2）将2015年的销售总额乘甲品牌剃须刀所占百分比即可.1.3×17%=0.221（万元）.

可见，由两个统计图组合的双统计图问题常常将许多条件隐含在不同的统计图中，这就需要我们读图时，一定要结合两幅统计图，进行双向联系，从图形中分析出有用的信息，获取相关的数据，找到解题的突破口，然后给出规范的解答过程.

（作者单位：江苏省兴化市昭阳湖初级中学）