理论力学教学中平面力系平衡的深入探讨

郑州大学力学与工程科学学院 何尚文

郑州工商学院建筑工程学院 唐华瑞 苗同臣

理论力学教学中平面力系平衡的深入探讨

郑州大学力学与工程科学学院 何尚文

郑州工商学院建筑工程学院 唐华瑞 苗同臣

总结平面力系平衡教学中的相关经验，结合具体实例深入分析平面汇交力系、平面平行力系、平面力偶系及平面任意力系平衡的联系与区别，总结出解决平面力系平衡问题的一般规律，揭示平面力系平衡的本质，使学生为后续知识学习奠定坚实的基础。

理论力学教学；平面力系；平衡方程；平衡

在理论力学教学中，力系平衡问题是非常重要的内容，它是后续相关力学课程学习的关键基础。使学生熟练掌握应用力系平衡方程解决各类工程问题的一般规律，深入透彻地理解力系平衡的本质，理清力系平衡涉及的关键观念，建立完整的知识体系是我们教学的核心目标。

1 平面力系的平衡方程

平面力系平衡问题是平面力系简化的深化和延续。根据平面力系简化的结论，力系平衡的充要条件为主矢和主矩同时为0。要区分力系平衡和系统平衡两个概念，系统平衡必有所受力系平衡，反之不一定成立。

平面任意力系的平衡方程，主矢、主矩同时为0，表达式如下（n为力系中力的个数）[1][2]：

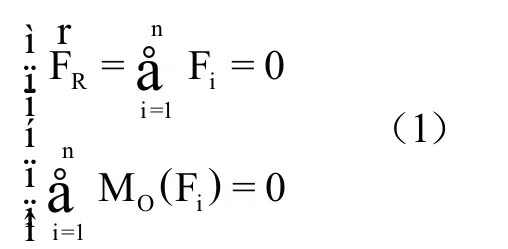
方程第一式为矢量方程；由于平面力系的矩可理解为标量，第二式为标量方程。

1.1 平面任意力系的独立平衡方程

对于平面任意力系，是平面上任意一点，将矢量方程描述为代数方程，则（1）式可写为式（2）[3]，即为平面任意力系的平衡方程，显然这3个代数方程是相互独立的。

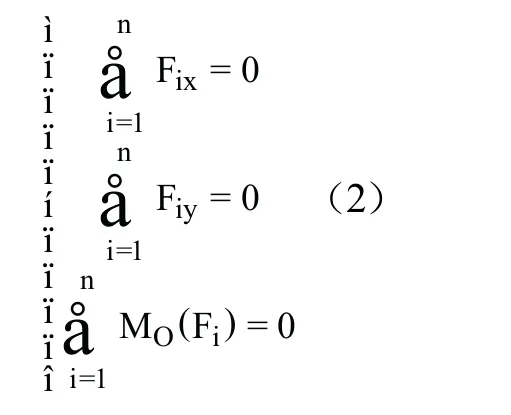
1.2 平面汇交力系的独立平衡方程

对于特殊的平面汇交力系，是平面上任意一点，是力系汇交点。其合力为通过汇交点的主矢，若此主矢为0，则对任意一点主矩自然为0，即平衡方程（2）中的第三式由前两式线性组合，同理第一式或第二式是也可由其他两式线性组合，相应平衡方程可写为式（3）或（4）[4]。

式（3）、（4）为平面汇交力系平衡方程的几种形式，两个独立方程，与式（2）比较可知平面汇交力系与平面任意力系平衡方程的区别与联系。

1.3 平面平行力系的独立平衡方程

对于特殊的平面平行力系，O是平面上任意一点。则平衡方程（2）中的前两式线性相关，平面平行力系的平衡方程可表达为式（5）[4]。

式（5）为平面平行力系2个独立的平衡方程。与式（4）比较可知，平面汇交力系与平面平行力系具有相同形式的平衡方程，可理解为平面平行力系是汇交点为无穷远点的特殊平面汇交力系。

1.4 平面力偶系的独立平衡方程

对于特殊的平面力偶系，其主矢自然为零，O是平面上任意一点。平衡方程（2）中前两式自动为零，则平衡方程形式转化为式（6）[5]，只有一个独立的平衡方程。

2 平面力系平衡方程典型例题分析

例：梯子上端B靠在铅垂墙壁上，下端A搁置在水平地面上，与墙壁之间为光滑约束，而与地面之间为非光滑约束。梯子与地面间的摩擦因数为fs，梯子重力为W，长为l。设梯子在倾角1位置保持平衡，求A、B处约束力FNA、和摩擦力FA。

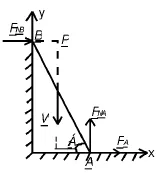
图1

图2

解一：按平面任意力系的平衡方程求解，3个平衡方程求解3个未知量。

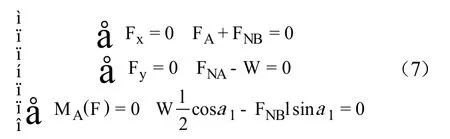
解二：按平面力偶系平衡方程求解，认为图中两个水平力与两个竖直力分别组成一个力偶，一个平衡方程，补充两个组成力偶的条件。

解三：如图2按平面汇交力系平衡方程求解。FNB与W汇交于P点，则全约束力必通过点，补充一个几何条件。设FRA与X轴负方向夹角为，则

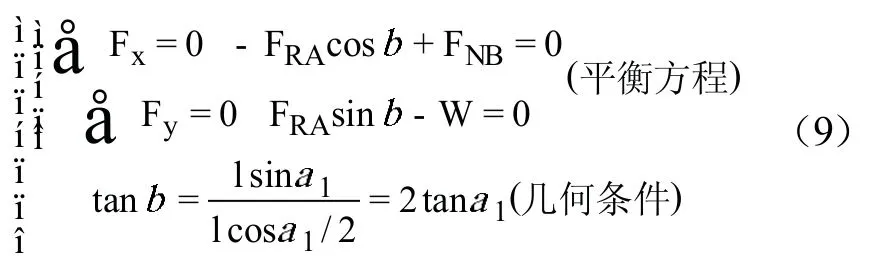
比较解一、解二与解三可知：式（8）中组成力偶的条件与式（7）中前两个平衡方程等价；式（9）与式（7）的3个方程（条件）完全等价，即式（7）、（8）、（9）完全等价，3种解法完全等价。

综上，平衡前提下平面力系可以看成平面任意力系、平面汇交力系、平面力偶系或平面平行力系；对一个研究对象其解决平衡问题的独立方程（条件）总是可以列出3个，要么是3个平衡方程，要么是1个或2个平衡方程加上其他方程（条件）；解决问题的方法取决于将该平面力系看成那种力系，n个构件组成的平衡系统总可列3n个独立方程（条件）。该结论可推广至空间力系平衡问题，也是文献[6][7]分析的进一步深化。

3 平面力系平衡的本质

理解力系平衡是从二力平衡的概念出发的，到三力汇交平衡，再到任意力组成的复杂力系的平衡。那么对于一个系统，其所受力系为任意的平面力系，其平衡的本质是什么呢？图1：看作平面任意力系，FNB与W汇交于p点，则其可合成为一个过p点的力FP，FA与FNA合成为通过A点的FRA，则该力系平衡可理解为FP与FRA二力平衡；若看作平面力偶系，与前分析相同，该平面任意力系依然可理解为FP与FRA二力平衡；图2：看作平面汇交力系，FNB与P汇交于点合成为力FP，则该力系平衡也可理解为FP与FRA二力平衡。

综上：任意一个平面力系的平衡均可理解为二力平衡，即从平衡的平面力系中任意选择一个力，则平衡一定可以看作力系中其余力的合力与该力的二力平衡；或者从平衡的平面力系中任意选择几个力，则平衡一定可以看作这几个力的合力与力系中其余力的合力组成的二力平衡。该结论可推至任意的空间力系平衡，将平衡的本质归结为二力平衡对于学生理解平衡问题有重要意义。

[1]哈尔滨工业大学理论力学教研室.理论力学（第7版）.北京:高等教育出版社,2009.

[2]洪嘉振,刘铸永,杨长俊.理论力学（第四版）.北京:高等教育出版社,2015.

[3]谢传锋,王琪.理论力学.北京:高等教育出版社,2009. [4]周又和.理论力学.北京:高等教育出版社,2015.

[5]刘延柱,杨海兴,朱本华.理论力学（第二版）.北京:高等教育出版社,2000.

[6]汪思伟.平面静力方程的独立性问题.重庆交通学院学报,1982，3（3）：106-112.

[7]李丰良.平面任意力系平衡方程的独立性.力学与实践,2001，3（23）：62-64.

0312.2

A

2017-01-05）

国家自然科学基金(51405452)、河南省高等学校重点科研项目(15A130002)资助.