复合功率分流混合动力汽车能量管理策略研究
2017-03-03沈登峰于海生易显科
沈登峰,王 晨,2,于海生,张 彤,易显科
(1.科力远混合动力技术有限公司,上海 201501; 2.同济大学新能源汽车工程中心,上海 200092)
复合功率分流混合动力汽车能量管理策略研究
沈登峰1,王 晨1,2,于海生1,张 彤1,易显科1
(1.科力远混合动力技术有限公司,上海 201501; 2.同济大学新能源汽车工程中心,上海 200092)
基于庞氏最小值原理,并以等效瞬时燃油消耗量最小为目标为某复合功率分流混合动力汽车制定了能量管理策略。利用MATLAB仿真平台,建立了混合动力系统能量管理策略的模型进行仿真。结果表明,与现有逻辑门限控制策略相比,采用等效瞬时燃油消耗量最小化的控制策略能显著提高燃油经济性。基于仿真结果,将控制策略集成到整车控制器中进行NEDC工况下的实车转鼓试验。结果显示,采用的控制策略使实车当量油耗降低了12.31%。
混合动力汽车;功率分流;能量管理策略;燃油经济性
前言
混合动力汽车相对于传统车辆能够有效降低燃油消耗和尾气排放。作为混合动力汽车典型类型的功率分流式混合动力汽车,由于其至少包含有发动机和动力电池在内的两个动力源,且需要合理分配各动力源之间的功率,所以开发出高效且鲁棒性强的能量管理控制策略是极其重要的[1]。作为常用的能量管理策略,最小值原理(pontryagin's minimum principle,PMP)、动态规划(dynamic programming,DP)和等效燃油消耗最小策略(equivalent consumption minimization strategy,ECMS)都能求解出能量管理的最优解。文献[2]和文献[3]中通过对比仿真结果得出,最小值原理的优化结果接近于动态规划的优化结果,且有效缩短了优化计算时间。文献[2]和文献[4]中结合具体工况通过假设初始拉格朗日算子经打靶法仿真求解得到最优解,虽然最小值原理能够缩短优化计算时间,但文献[2]和文献[4]中指出最小值原理不适用于工况无法预知的乘用车。文献[1]和文献[5]中指出,由于等效燃油消耗最小策略从根本上可描述为欧拉-拉格朗日方程,且等效燃油消耗最小策略中的等效油耗可更好地被理解为最小值原理中的哈密顿函数,所以可将其视为最小值原理控制在实车控制中的应用。通过引入基于SOC的惩罚函数,文献[6]中解决了因单纯的ECMS算法无法将动力电池的SOC控制在理想工作区间内的问题。文献[1]、文献[4]和文献[5]中均选择动力电池功率为控制变量,SOC为状态变量。选取动力电池功率作为控制变量,实际是通过控制功率分配来决定混合动力系统的能量分配。通过预估回路中的电机功率,确定电机转速和转矩,进而得到实际回路中的电机功率,然而预估功率与实际功率之间的误差导致SOC计算不准确。
上述文献大多针对并联式混合动力汽车进行能量管理策略的仿真研究,并未对复合功率分流式混合动力汽车进行能量管理策略仿真研究后的试验验证。因此,本文中首先对某新型功率分流式混合动力系统进行结构设计,基于结构设计建立数学模型,并对其工作模式进行分析,然后通过等功率法对发动机模型进行优化,并通过基于规则的控制策略与整车模型联合仿真建立了SOC与当量燃油消耗量之间的油电转化关系,接着基于最小值原理得到等效瞬时燃油消耗量的目标函数,最终经过Matlab/ Simulink平台下仿真分析和实车转鼓试验验证本文中提出的能量管理控制策略。
1 复合功率分流混合动力系统方案
1.1 结构设计
如文献[7]中所述,该新型复合功率分流式混合动力系统采用共用行星架和齿圈的双行星排结构,发动机与混合动力变速器中的行星架通过扭转减振器相连,电机E1和电机E2分别与混合动力变速器中的小太阳轮S1和大太阳轮S2相连。制动器B1和制动器B2分别用于锁止行星架和电机E1。动力电池依据电机控制器的控制,驱动电机或储存电机产生的电能。图1为该新型功率分流式混合动力系统结构图,图2为其实物图。表1为整车参数和动力部件参数。

图1 新型复合功率分流式混合动力系统结构图

图2 新型复合功率分流式混合动力系统实物图

表1 整车和动力部件参数
1.2 数学模型
结合文献[7]中所述动力学、运动学方程和电功率平衡方程,得到该新型功率分流式混合动力系统的数学模型:

式中:TPC,JPC和αPC分别表示行星架PC的转矩、转动惯量和角加速度;TS1,JS1和αS1分别表示小太阳轮S1的转矩、转动惯量和角加速度;TS2,JS2和αS2分别表示大太阳轮S2的转矩、转动惯量和角加速度;TR,Jout和αR分别表示外齿圈R的转矩、输出轴转动惯量和角加速度;TICE,TE1和TE2分别表示发动机、电机E1和电机E2的转矩;TL表示整车的行驶阻力矩;PB表示动力电池功率;PVB,PVB1和PVB2分别表示动力电池、电机E1和电机E2的损耗功率; ωE1和ωE2分别表示电机E1和电机E2的角速度。
1.3 工作模式
双行星排动力系统具有5种工作模式[8],如图3所示,分别为模式1纯电动驱动、模式2发动机起动、模式3制动能量回收、模式4混合动力驱动和模式5 B2锁止混合动力驱动。

图3 新型复合功率分流式混合动力变速器转速和转矩杠杆原理图
2 基于最小值原理的等效燃油消耗最小能量管理控制策略设计
2.1 发动机模型优化
在发动机模型中,发动机工况点及其燃油消耗量由转速nICE和转矩TICE决定。对新型复合功率分流式混合动力汽车而言,通过行星排机构可实现发动机转速与整车车速解耦,发动机拥有转速与转矩两个自由度。如文献[9]中所述,对于e-CVT混合动力汽车,发动机热损失远大于电路功率损耗,以发动机工作在优化工作点(最佳效率点)为控制目标是合理的。本文中采用基于发动机功率的方式确定发动机最优工作曲线[9]:
(1)发动机功率范围内,均分为P1,P2,…,Pk,…,Pm等m个功率点;
(2)对于某个功率点Pk,发动机等功率曲线上多个工况点满足TICE×nICE=Pk,每个工况点对应燃油消耗率be(Pk),从多个工况点中寻找发动机油耗量最低的点Qk;
(3)在多个功率点下,求得对应发动机油耗量最低点Q1,Q2,…,Qk,…,Qm,油耗最低点顺序相连所得到的曲线为发动机最优工作曲线。
图4为基于发动机功率得到的发动机最优工作曲线。
2.2 油电转化系数
油电转化系数是单位动力电池SOC变化量对应的发动机燃油消耗量,单位为g/(100%SOC)。油电转化系数作为动力电池电量与发动机油耗之间的转化因子,可表示动力电池电量对整车助力能力与续航能力的影响。本文中结合基于逻辑规则的整车控制策略与整车模型联合仿真,建立SOC与当量燃油消耗量在NEDC工况下的转化关系,仿真结果如表2所示。

图4 发动机最优工作曲线

表2 不同初始SOC下燃油修正系数仿真数据
按照国标[10]要求,由式(2)计算得到燃料消耗量修正系数Kfuel=0.857 3(L/100km)/(A·h)。

式中:Ci为第 i次试验时测得的燃料消耗量, L/100km;Qi为第i次试验的电量平衡值,A·h,电池充电为正值,放电为负值;n为数据个数,n≥6。
根据油电转化系数的含义,其与燃料消耗量修正系数Kfuel的换算关系为
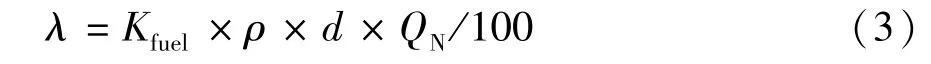
式中:ρ为92#汽油密度,ρ=730 g/L;d为NEDC运转循环行程总驾驶里程,d=11.022 7km;QN为电池额定容量,QN=6A·h。由式(3)算得
λ=413.89[g/(100%SOC)]
2.3 基于最小值原理的等效燃油消耗最小能量管理控制策略求解方法描述
为克服文献[1]、文献[4]和文献[5]中研究的局限,结合该系统的数学模型和发动机优化模型,选取发动机转速为控制变量,SOC为状态变量,将该系统简化为单自由度控制问题,即

针对在一段有限时长为[t0,tf]的循环工况下燃油消耗最小的控制,选取性能指标函数为积分型性能指标函数,可表示为
式中L(x(t),u(t),t)为与发动机状态有关的瞬时燃油消耗量,可表示为

式中PICE为发动机瞬时功率。
控制变量u(t)的控制域为

状态变量x(t)的初始条件为

由该系统采用的镍氢动力电池参数可知,SOC的调节范围必须被约束在电池内阻最小、热损耗最少的常用工作区间,所以状态变量x(t)的约束条件为

由镍氢动力电池模型和安时计量法可得SOC变化量:

则系统的状态方程为

至此,复合功率分流式混合动力系统能量管理控制策略的问题可描述为在一段有限时长为[t0,tf]的循环工况里,在状态变量x(t)的约束条件下,在控制变量 u(t)的控制域中寻求一系列控制规则u(t),使燃油消耗最小和电池SOC维持在最佳工作区间内,其具体目标函数和约束条件为

根据式(13)建立哈密顿函数:


式中λ(t)为伴随乘子向量函数。
式(14)可以进一步化简为

根据文献[6],需要满足如下条件才能运用最小值原理获得燃油消耗最小的能量管理控制策略。
(1)在一段有限时长为[t0,tf]的循环工况里,存在最佳控制变量u*(t)∈[nICE(t)min,nICE(t)max]使H(x*,u*,λ,t)成为全局最优解,即
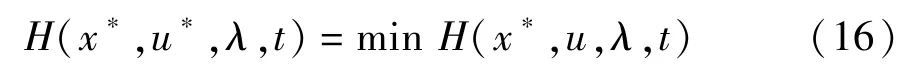
(2)系统满足边界条件,即

如文献[1]中所述,由于镍氢动力电池的内阻和充放电电压在一定SOC范围内可近似看作不变,所以动力电池电流只与动力电池功率有关,与SOC无关,即

由于最小值原理的优化算法需要提前预知整个循环工况,无法运用在车辆的实际控制中。为克服该局限,现将基于该优化算法扩展出的等效燃油消耗最小能量管理控制策略运用于实时控制。
等效燃油消耗最小实时优化能量管理控制策略(ECMS)的核心是构造能表征每个时刻下发动机燃油消耗量与等效燃油消耗量之和最小的实时优化目标函数。为减少因打靶法带来的庞大计算量,同时又能使算法更符合车辆的实际运行状况,取λ为覆盖城市和郊区工况的NEDC循环的油电转化系数时,在基于最小值原理等效燃油消耗最小能量管理控制策略中构建的哈密顿函数恰好准确地描述该实时优化目标函数。在该哈密顿函数的前半部分为发动机的瞬时燃油消耗量,后半部分为动力电池电量增加或者减少对应的等效瞬时燃油消耗量,两部分之和即为等效燃油消耗最小实时优化能量管理控制策略的目标函数。通过求解当前瞬时哈密顿函数的最小值,进而求解出该最小值所对应的控制变量nICE(t)。
本文中引入基于动力电池SOC的惩罚函数,用于调整控制策略对电能使用的倾向。本文中采用的惩罚函数是由三次曲线函数和四次曲线函数拟合而成的分段S形曲线函数,如图5所示。设该惩罚函数的表达式为

其中DEVSOC=SOC-(SOCL+SOCH)/2
式中:SOCL为理想工作区的下限值;SOCH为理想工作区的上限值。

图5 SOC惩罚函数
通过修改函数中参数a和b的值对惩罚函数的形状进行调整,具体的函数表达式如下。
当DEVSOC≥0.2,即SOC≥0.7时,

当DEVSOC<-0.2,即SOC<0.3时,

当 -0.2≤DEVSOC<0.2,即0.3≤SOC<0.7时,

因此,经SOC惩罚函数修正后的动力电池SOC变化量对应的等效油耗为

等效燃油消耗最小实时优化算法实现流程如图6所示。
具体描述:在当前控制变量和状态变量的允许范围内,根据当前动力电池的SOC查表得到动力电池的内阻、开路电压等关键参数。将控制变量的可行域等分,任一可行域内的等分点对应着一个最优的发动机转矩值。根据当前的车速、整车需求转矩和可行域的等分点及其对应的发动机转矩,利用该系统的数学模型可以求得两个电机对应的转速和转矩,再结合动力电池此刻的关键参数值、惩罚函数值和油电转化系数可求得到当前的瞬时等效油耗量。该瞬时等效油耗量和发动机当前瞬时油耗量之和最小值所对应的发动机转速和转矩,即为当前时刻混合驱动模式下发动机的最优工作点。由于车速小于100km/h时,整车可处于纯电动模式,所以当车速小于100km/h时,等效燃油消耗最小实时优化算法还会利用类似上述的算法去求解满足当前驱动需求的纯电动瞬时等效油耗量。通过对比混合驱动模式下的等效燃油消耗和纯电动模式下的等效燃油消耗,进而可以控制车速低于100km/h时是否起动发动机。

图6 等效燃油消耗最小实时优化算法流程图
3 仿真结果与分析
本文中在Matlab仿真平台上采用.m文件和Simulink联合仿真,得到NEDC工况下的等效燃油消耗最小实时优化能量管理控制策略和现有逻辑控制算法能量管理策略的控制效果。
3.1 仿真结果分析
图7为NEDC工况初始SOC为0.7时逻辑控制算法能量管理策略和等效燃油消耗最小实时优化能量管理控制策略仿真结果对比图。

图7 逻辑控制算法和等效燃油消耗最小实时优化算法仿真结果对比
逻辑控制算法能量管理策略中发动机起动次数多,每次起动后发动机工作时间短,发动机转速高。等效燃油消耗最小实时优化能量管理控制策略通过调整发动机的起停时机,在整个行驶工况中优先使用动力电池驱动,当SOC偏低时,在惩罚函数的作用下整车起动发动机,利用发动机满足整车驱动,避免在低驱动功率需求下起动发动机。同时根据2.1节优化得到的发动机工作曲线,在该工况下发动机总是被控制在最优工作点,提高了燃油经济性。
表3为初始SOC为0.7时两种算法能量消耗结果对比。相比现有逻辑控制策略,通过ECMS算法得到初始SOC为0.7的NEDC工况最优控制策略,当量油耗可降低21.47%。

表3 ECMS与逻辑算法能量消耗结果
3.2 能量管理控制策略的实车应用

图8 不同SOC下车速小于100km/h的发动机工作模式标志位
由于基于最小值原理瞬时等效燃油消耗最小能量管理控制策略的计算量较大,运算周期长,无法直接移植到现有的实车控制器中进行应用。为了能够发挥基于最小值原理瞬时等效燃油消耗最小能量管理控制策略的优势,同时又能达到在实车控制单元中使用的目的,现将其在每个SOC下仿真计算得到的发动机起停标志位和发动机最优工作点的结果拟合成车速和加速踏板开度的函数,并制成map图植入到整车控制单元中,通过车速信号和加速踏板开度信号查表来进行实车控制。图8为在每10%SOC间隔下车速低于100km/h时发动机工作模式标志位Mod_flg的map图。当Mod_flg等于1时发动机须起动,整车须处于混合驱动模式;反之,整车须处于纯电动模式。图9为在每10%SOC间隔下车速低于100km/h时发动机最优工作转速点。图10为在每10%SOC间隔下车速高于100km/h时发动机最优工作转速点。

图9 不同SOC下车速小于100km/h的发动机最优工作转速点
4 试验验证与分析
在初始SOC为0.7,发动机温度高于80℃的条件下开始转鼓油耗试验。图11为整车转鼓试验图。试验中数据通过ETAS公司的软件INCA和硬件ES592进行采集。
图12为基于现有的整车逻辑控制策略和基于ECMS算法整车逻辑控制策略进行的NEDC油耗试验结果对比图。试验结束时,逻辑门限控制策略下的SOC下降了0.15,发动机100km油耗为6.62L,等效100km油耗为7.39L。ECMS控制策略下的SOC下降了0.39,发动机100km油耗为4.45L,等效100km油耗为6.48L。

图10 不同SOC下车速高于100km/h的发动机最优工作转速点

图11 整车转鼓试验图
相比原有策略,采用ECMS算法控制策略时,在NEDC城市驾驶循环下大部分使用纯电动模式运行,减少了发动机的起停次数,仅在SOC较低时起动发动机,避免发动机工作在整车需求功率较低的工况,从而降低发动机实际油耗。在城郊工况下,发动机运转在最优工作点,其功率基本满足整车驱动功率,动力电池在中低速阶段提供助力功率,在高速阶段充电并回收能量。总的效果为当量油耗降低了12.31%。
试验结果表明,中、低速下使用动力电池驱动,高速下利用发动机满足整车驱动功率需求的能量管理策略有利于降低整车的能量损耗。

图12 逻辑算法和ECMS算法NEDC油耗试验
5 结论
本文中旨在提出一种基于最小值原理适用于新型复合功率分流混合动力汽车的实时优化能量管理控制策略。通过对该混合动力系统进行结构分析,构建其数学模型,结合优化发动机模型,确定了以SOC为状态变量,以发动机转速为控制变量的算法优化方案。基于最小值原理的哈密顿函数,结合NEDC工况下的油电转化系数,得到等效燃油消耗最小实时优化能量管理控制策略的实时优化目标函数。通过引入基于动力电池SOC的惩罚函数,用于调整控制策略对电能使用的倾向。仿真结果和试验结果均表明,基于最小值原理的等效燃油消耗最小能量管理控制策略明显减少了燃油消耗。与原有逻辑控制策略相比,在SOC初始值为0.7和NEDC循环工况条件下所得到的基于最小值原理的等效燃油消耗最小能量管理控制策略可降低12.31%的当量油耗。
[1] KIM N,CHA S,PENG H.Optimal control of hybrid electric vehicles based on pontryagin's minimum principle[J].Control Systems Technology IEEE Transactions on,2011,19(5):1279-1287.
[2] YUAN Z,TENG L,SUN F,et al.Comparative study of dynamic programming and pontryagin's minimum principle on energy management for a parallel hybrid electric vehicle[J].Energies,2013, 6(4):2305-2318.
[3] ZHENG C H,XU G Q,PARK Y I,et al.Comparison of PMP and DP in fuel cell hybrid vehicles[J].International Journal of Automotive Technology,2014,15(1):117-123.
[4] JEONG J,LEE D,KIM N,et al.Development of PMP-based power management strategy for a parallel hybrid electric bus[J].International Journal of Precision Engineering&Manufacturing,2014, 15(2):345-353.
[5] KIM N W,LEE D H,ZHENG C,et al.Realization of pmp-based control for hybrid electric vehicles in a backward-looking simulation [J].International Journal of Automotive Technology,2014,15 (4):625-635.
[6] 林歆悠.混联式混合动力客车功率均衡能量管理控制策略研究[D].重庆:重庆大学,2011.
[7] 王晨,赵治国,张彤,等.复合功率分流式e-CVT结构优化及验证[J].中国公路学报,2015,28(3):117-126.
[8] YU H S,ZHANG J W,ZHANG T.Control strategy design and experimental research on a four-shaft electronic continuouslyvariable transmission hybrid electric vehicle[J].Proceedings of the Institution of Mechanical Engineers,Part D:Journal of Automobile Engineering,2012,226(12):1594-1612.
[9] DEBERT M,COLIN G,CHAMAILLARD Y,et al.Energy management of a high efficiency hybrid electric automatic transmission [C].SAE Paper 2010-01-1311.
[10] 全国汽车标准化技术委员会.GB/T 19753—2013轻型混合动力电动汽车能量消耗量试验方法[S].北京:中国标准出版社,2014.
A Study on Energy Management Strategy for Compound Power-split Hybrid Electric Vehicle
Shen Dengfeng1,Wang Chen1,2,Yu Haisheng1,Zhang Tong1&Yi Xianke1
1.Corun Hybrid Technology Co.,Ltd.,Shanghai 201501; 2.Clean Energy Automotive Engineering Center,Tongji University,Shanghai 201804
Based on Pontryagin's minimum principle and with minimizing equivalent instantaneous fuel consumption as objective,the energy management strategy for a compound power-split hybrid electric vehicle is formulated.A model for that energy management strategy of HEV is set up with MATLAB platform and a simulation is conducted.The results indicate that compared with existing logic threshold control strategy,using equivalent instantaneous fuel consumption minimization strategy can significantly enhance fuel economy.Based on simulation results, the control strategy formulated is integrated into vehicle controller and a real vehicle drum test is performed under NEDC driving cycle with a result showing that using the control strategy formulated make the equivalent fuel consumption of vehicle reduces by 12.31%.
HEV;power-split;energy management strategy;fuel economy
10.19562/j.chinasae.qcgc.2017.01.003
原稿收到日期为2016年1月6日,修改稿收到日期为2016年3月10日。
沈登峰,博士研究生,E-mail:dengfeng.shen@campus.tu-berlin.de。
