基于EMD的GM-LSSVM在变形预测中的应用

陆杰，梁月吉，徐宁辉，陶健春

(1.南宁勘察测绘地理信息院，广西 南宁 530001； 2.桂林理工大学测绘地理信息学院，广西 桂林 541004； 3.广西城市建设学校，广西 桂林 541003)

基于EMD的GM-LSSVM在变形预测中的应用

陆杰1*，梁月吉2，徐宁辉1，陶健春3

(1.南宁勘察测绘地理信息院，广西 南宁 530001； 2.桂林理工大学测绘地理信息学院，广西 桂林 541004； 3.广西城市建设学校，广西 桂林 541003)

针对变形呈非线性、随机性变化特征，提出了一种基于经验模态分解(EMD)的灰色最小二乘支持向量机(GM-LSSVM)变形预测模型。该模型首先采用EMD有效分离出隐含在变形序列中的非线性高频成分和低频成分；然后根据各分量特点构建了高频LSSVM预测模型和低频GM(1，1)预测模型，最后叠加各分量预测值得到预测结果。经理论分析和算例表明，并与灰色GM(1，1)、BP神经网络和LSSVM对比分析。结果表明，EMD能够有效分离变形序列的不同频率成分，本文方法具有较强的预测精度，均方根误差为 0.40 mm，在变形预测中具有一定的实用价值。

大坝变形；经验模态分解；GM(1，1)；最小二乘支持向量机；精度评定

1 引 言

大坝变形往往受水位、温度等多种因素共同影响，具有一定的非线性和随机性变化，为保证大坝以及人类的安全，需要及时掌握大坝变形状态并及时做出准确预测。目前，常用的预测方法主要有时间序列分析、灰色理论、BP神经网络和支持向量机等，以上方法均存在一定的局限性。灰色预测模型具有所需数据少、建模简单等特点，适合用于解决呈指数增长趋势的实际问题，而对于复杂变化、随机变化的序列，预测误差较大[1]；人工神经网络在大坝变形分析中得到了较为广泛的应用[2]，但其易陷入局部极小点、模型结构不易确定、泛化能力不强或过于学习等。赵洪波等[3]将支持向量机引用到变形预测中，解决了多因素影响下的复杂变形预测问题，预测精度得到了进一步提高。然而，由于大坝变形受多种因素共同影响，直接通过建立变形量与影响因素之间的复杂非线性关系模型难以保证模型预测的准确性。 Huang等[4]于1998年提出了一种新的信号处理EMD方法。该方法是一种处理非线性和非平稳信号的自适应分解方法，不需要确定任何函数，直接对信号进行平稳化处理，能够有效提取原信号的波动项和趋势项[5]。基于上述研究，本文提出了基于经验模态分解(EMD)和灰色最小二乘支持向量机(GM-LSSVM)的大坝变形预测方法。通过算例，证实其有效性和可行性。

2 基于EMD的GM-LSSVM变形预报模型

2.1 经验模态分解法

经验模态分解(Empirical Mode Decomposition，EMD)是一种自适应信号分解方法，能够将存在于原始序列中不同特征的趋势逐级筛选出来，得到具有相同特征尺度的固有模态分量(Intrinsic Mode Function，IMF)，IMF必须同时满足两个条件[4，5]：第一，在待分解信号中，极值点的数目与过零点的数目相等，或最多相差一个；第二，在任一时间上，由局部极大值和局部极小值定义的包络均值为零。具体分解过程可参考文献[4，5]。2.2 灰色GM(1，1)

灰色GM(1，1)是一个单个变量预测的一阶微分方程模型，其离散时间响应函数近似指数规律。建模的思路：大坝水平位移变形序列经过一次累加，形成一个递增数列，经不断累加，形成的数据点连线后接近于某个指数函数，然后通过这个指数函数外推到下一个累加和，再累减还原即得到大坝序列预测值。

2.3 最小二乘支持向量机

设某变形序列的样本集为{(xi，yi)|xi∈Rn，yi∈R，i=1，2，…，l)}，得到LS-SVM的回归函数为[6]：

y(x)=wTφ(x)+b

(1)

式中，φ(x)表示能够满足Mercer条件的核函数，w表示超平面的权值向量，b表示偏置顶。

对于最小二乘支持向量机的估计问题，将回归问题等价为最小化得到：

(2)

式中，γ表示正则化参数，ei表示误差项。构建式(2)的Lagrange函数得到：

(3)

式中，a=[a1，a2，…，al]T。根据 KKT(Karush-Kuhn-Tucker)条件，计算Lagrange函数的最优解：

(4)

对式(4)进行简化，得到的线性方程组为：

(5)

式中，y=[y1，y2，…，yl]T，A=[1，…，1]T，I表示单位矩阵，K(xi，yi)表示满足Mercer条件的核函数。

设B=K(xi，yi)+γ-1I，采用最小二乘运算求解式(5)得到：

(6)

得到LSSVM的估计函数为：

(7)

2.4 LSSVM参数的优化

由2.3可知，核函数k()的选择以及核参数σ和正则化参数γ的优化直接影响到最小二乘支持向量机的预测精度。因此，本文选取径向基函数作为模型的核函数，该核函数能够较好地反映模型的复杂程度，采用网格搜索法对σ和γ参数进行优化。参数优化步骤如下[7]：

(1)设定参数σ和γ的选择范围、参数步长、网格间隔、网格点目标函数值的计算等。

(2)根据σ和γ的初始值，选择第一个交叉验证网点位置，通过交叉验证方法获取训练均方误差作为网格点计算的目标函数，并计算所有的网格点。

(3)选取均方误差最低的一组(σ，γ)为最优参数。若选取的参数达不到精度要求，则以选择的参数为中心网格点，在较小的范围内构建新的二维网格平面重新计算目标函数，再次选取均方误差最低的参数。如果满足精度要求，则停止，否则继续重复以上步骤，最终获取精确的参数σ和γ作为最优值。

2.5 预测流程

本文模型预测流程如下：

(1)采用EMD对大坝变形序列进行分解，得到n个IMF高频分量和1个低频分量DF。

(2)针对各IMF，建立相应的LSSVM预测模型，同时建立灰色GM(1，1)预测模型对DF低频序列进行预测。

(3)对各模分量预测的残差进行组合即得到最终的预测结果。

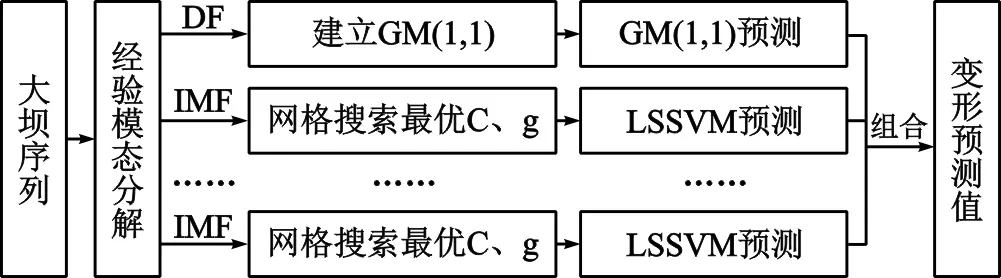
图1 模型预测流程图

3 模型精度评定

本文采用均方根误差和平均绝对值误差来评定模型预测精度[1]：

(8)

(9)

4 算例分析

本文以某大坝水平位移变形监测数据为实验数据[9]，监测期为91期，如图2所示。可见，该大坝水平位移变形变化不稳定，非线性和随机性变化较强，难以直接建立较为准确的预报模型。因此，为探讨大坝变形序列的特征，采用EMD进行分解，分解结果如图3所示。由图3可见，EMD将变形序列分解为4个频率依次降低的分量，其中IMF1分量具有一定的非线性变化，IMF2和IMF3呈现出周期性和随机性成分，DF体现出变形序列的整体变化趋势。显然，根据各分量建立对应的模型，对提高预测精度具有较大的可能。

为验证本文方法的有效性和可行性，建立4种方案进行对比分析：方案1—灰色GM(1，1)预测模型、方案2—BP神经网络预测模型、方案3—最小二乘支持向量机预测模型、方案4—基于EMD的GM-LSSVM预测模型。各方案采用前71期变形数据作为模型训练输入，后20期作为模型预测数据。方案1～方案3直接采用原始变形预测进行建模，方案4采用经EMD分解得到的各分量进行建模。同时，为了减少建模误差，本文统一将变形序列归化到[-1，1]区间，再进行建模预测。各分量的预测结果图4所示。

图2 大坝变形水平位移序列

图3 EMD分解结果

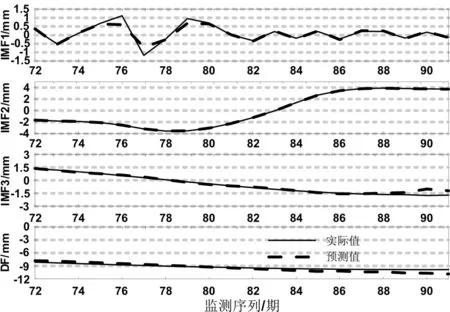
图4 各分量预测值和实际值对比

由图4可得，方案4的预测结果和实际分量相吻合，预测精度较高。各方案预测结果如表1和图5所示。

由表1可见，方案1、方案2和方案3的预测结果不稳定，部分预测值和实际值相差比较大，GM(1，1)的最大残差为 4.33 mm，BP神经网络的最大残差达到 3.96 mm，LSSVM的最大残差为 2.73 mm。而方案4的预测结果均优于其他方案，残差最小值为 0.04 mm，最大值仅为 0.81 mm。结合图5进一步看出：GM(1，1)不能正确反映变形的趋势，过于线性拟合预测；BP神经网络由于自身的缺陷，预测结果波动较大；LSSVM的部分预测结果不稳定，而本文方法的预测结果比较稳定，接近于大坝实际值。可见，采用经验模态分解离使得变形序列中不同频率的成分得到有效分离，预测模型的自身性能得到充分发挥。本文方法综合结合线性和非线性的拟合能力，预测结果更能显示大坝变形的趋势。

不同方案的预测结果对比 表1

图5 各方案的预测值和大坝实际变形值对比

各方案的预测精度统计如表2所示。

各模型精度对比(单位/mm) 表2

由表2进一步发现，方案4的预测精度最高，均方根误差和平均绝对误差分别为 0.40 mm、 0.34 mm。可见，基于EMD的GM-LSSVM预测模型保证了较好的全局预测精度，更具优越性。综上，采用经验模态分解能够有效分离隐含在变形序列中的特征成分，更有利于模型的建立和预报。正是本文方法综合考虑了变形的特征，充分发挥了模型的线性和非线性预测能力，无论在预测结果还是预测精度上均优于单一的GM(1，1)、BP神经网络和最小二乘支持向量机。

4 结 论

本文提出基于EMD的GM-LSSVM变形预测方法，结果表明：经验模态分解能够有效分离隐含在时序中隐含的非线性和随机性高频成分以及趋势低频成分；各分量更加明显地表现出时序中隐含的特征信息，使得GM-LSSVM预测模型的自身性能得到充分发挥。本文方法具有较强的拟合预测能力，预测精度较高。

[1] 任超，梁月吉，庞光锋等. 最优非负变权组合模型在大坝变形中的应用[J]. 大地测量与地球动力学，2014，34(6)：162～166.

[2] 刘勇健，李彰明，张建龙等. 基于遗传-神经网络的深基坑变形实时预报方法研究[J]. 岩石力学与工程学报，2004，23(6)：1010～1014.

[3] 赵洪波. 支持向量机在隧道围岩变形预测中的应用[J]. 岩石力学与工程学报，2005，24(4)：649～653.

[4] Huang N E，Shen Z，Long S R. The Empirical Mode Decomposition and Hilbert Spectrum for Nonlinear and Nonstationary Time Series Analysis[J]. Proceedings of the Royal Society of London SERIESA，1998，903～995.

[5] 戴吾蛟，丁晓利，朱建军等. 基于经验模式分解的滤波去噪法及其在 GPS多路径效应中的应用[J]. 测绘学报，2006，35(4)：321～327.[6] Suykens J A K，Vandewalle J. Least Squaresupport Vector Machine Classifiers[J]. Neural Processing Letters，1999，9(3)：293～300.

[7] Liu Xianglou，Jia Dongxu，Li Hui. Research on Kernel Parameter Optimization of Support Vector Machine in Speaker Recognition[J]. Science Technology and Engineering，2010，10(7)：1669～1673.

[8] 姜成科. 基于遗传算法的神经网络在大坝变形预报中的应用[D]. 大连：大连理工大学，2009.

GM-LSSVM Based on EMD in The Application of the Dam Deformation

Lu Jie1，Liang Yueji2，Xu Ninghui1，Tao Jianchun3

(1.Nanning Exploration & Survey Geoinformation Institute，Guilin 530001，China； 2.College of Geomatics and Geoinformation，Guilin University of Technology，Guilin 541004，China； 3.Guangxi Urban Construction School，Guilin 541003，China)

A new algorithm based on empirical mode decomposition (EMD)and the grey least squares support vector machine (GM-LSSVM)for dam deformation prediction was presented. Firstly，to effectively separate the nonlinear trend of volatility of high frequency component and low frequency one，the algorithm deformation sequence was decomposed by EMD；Then，the LSSVM was applied to build a prediction model for high frequency component，and the GM(1，1)was applied to build a prediction model for low frequency one；Finally，the predicted values of each component in the forecast was overlay. The calculation result was analyzed and compared with the grey GM(1，1)、BP neural network and LSSVM. The results show that the EMD can effectively separate different frequency components of deformation sequence，prediction accuracy of the method is stronger，root mean square error is 0.40mm，which can be applied to dam deformation prediction practically.

dam deformation；empirical mode decomposition；GM (1，1)；least squares support vector machine；precision evaluation

1672-8262(2017)01-142-04

P196，TV698.11

B

2016—05—07 作者简介：陆杰(1978—)，男，工程师，主要从事测绘工程技术工作。 基金项目：广西自然科学基金项目(2014GXNSFAA118288)；广西“八桂学者”岗位专项经费资助项目、广西空间信息与测绘重点实验室资助课题(桂科能130511402，130511407)。