改进BP神经网络模型在隧道变形分析中的应用

郭松，陆金平，邹瑜

(江西应用技术职业学院，江西 赣州 341000)

改进BP神经网络模型在隧道变形分析中的应用

郭松*，陆金平，邹瑜

(江西应用技术职业学院，江西 赣州 341000)

针对传统的BP神经网络模型在数据拟合方面存在网络收敛速度慢，预测精度不高的缺点，提出一种改进的BP神经网络模型的方法。利用改进后的模型对某一地铁隧道变形监测数据进行分析和预报，并结合MATLAB软件编写的数据处理程序实现改进前后两种模型对同一数据处理结果的对比分析，验证改进后模型的有效性和可靠性。

变形监测；神经网络；BP神经网络；MATLAB

1 绪 论

人工神经网络(Artificial Neural Network，即ANN)的快速发展使其开始在各个领域得到广泛应用，其主要特点是：信息不储存在确定的单元中，而是分散储存在整个系统中；同时，它具有较好的鲁棒性和容错性，能够对不完整的样本数据和图形做出判断；能够对任意的非线性系统进行逼近；具有学习和自适应等功能，对复杂多变的系统动态特性有很强的适应性。正是以上这些优点，使得人工神经网络在变形监测的数据处理分析中能够得到较好的应用。

本文以ANN模型中的BP神经网络预测模型为切入点，阐述了改进后的BP神经网络预测模型的确定。同时，对比BP神经网络预测模型与改进后的模型，并结合工程实例验证该改进方法的合理性。

2 BP神经网络的模型

2.1 建模机理

BP神经网络的学习算法为误差反向传播算法，即BP算法，它的学习训练过程主要包括四个阶段。

(1)第一阶段为顺序传播过程，即网络样本数据由输入层经过隐含层的信息处理和信息变换，再将隐含层的输出结果传递给输出层的过程；

(2)第二阶段为反向播过程，即对比网络的输出结果与期望值之差，然后按照减小误差的方向，再由输出层传递给隐含层，隐含层依据误差的大小进行调整和修正它们之间的连接权值，最后返回到输入层的过程；

(3)第三阶段为记忆训练过程，即重复第一和第二阶段的过程；

(4)第四阶段为网络的收敛过程，即网络的误差趋向极小值发展的过程。

①初始化。在[-1，+1]的区间内随机选取各连接权值和阈值；

②随机选取样本数据对(Xk，Yk)代表网络的输入向量；

③计算输入层的输出。由于输入层本身不进行数据处理，因此输入层的输出向量仍然为输入的样本数据；

④根据式(1)和式(2)对输入的样本数据进行处理，从而得到隐含层各个神经元的净输入和输出；

(1)

(2)

⑤根据式(3)和式(4)对输出层各个神经元的净输入和实际输出进行计算；

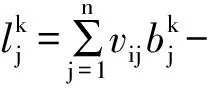
(3)

(4)

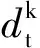
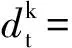
(5)

(6)

⑧按照式(7)和式(8)对连接权值V和阈值γ进行修正，其中α为学习速率，0<α<1；

(7)

(8)

⑨按照式(9)和式(10)对输出层的连接权值W和阈值θ进行修正，其中β为学习速率，0<β<1；

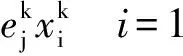
(9)

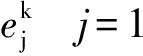
(10)

⑩随机选取另一个样本数据对再作为输入向量，直到所有样本数据对训练完毕为止；

2.2 模型的不足

经过长期的理论和实践，对BP神经网络算法的缺点进行总结概括，主要有以下几点缺点：

(1)学习算法的收敛速度慢。BP神经网络学习训练过程是样本数据一次次地反复处理过程，只有当全局误差小于要求精度时，学习训练才会结束，因此，学习训练的过程比较漫长，导致网络的收敛速度缓慢；

(2)存在局部极小点；

(3)选取合适的隐含层节点个数时缺乏具体的理论指导；

(4)对于新的样本数据要重新进行训练学习。

3 BP神经网络的改进方法

3.1 增加动量项的BP算法

传统的BP神经网络算法在对连接权值进行调整时，由于没有考虑到前一次调整时的误差梯度方向，而只考虑本次的误差梯度下降方向，就导致了网络收敛速度缓慢。为了提高网络的收敛速度，就必须考虑前一次调整时的误差梯度方向，然后把前一次调整量按一定的比例加在本次调整中，即动量项。接权值调整公式如下：

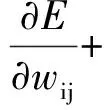
(11)

式中，μ△wij(n-1)表示动量项，n表示学习次数，μ表示动量系数，0<μ<1，η表示学习率。

当在调整连接权值时附加动量项，就会使调整方向向一个方向发展，即是两次调整的方向相反，仍然可以提高网络的收敛速度。

3.2 自适应调整学习率的优化算法

在BP神经网络的整个训练学习过程中，学习速率对BP网络学习算法有相当大的影响。当学习速率偏大时，就会造成学习的过程振荡且网络不收敛；当学习速率偏小时，则造成网络的收敛速度变慢并且网络的学习训练时间过长。因此，选择一个合适的学习速率，可以有效提升BP神经网络的学习训练时间和网络收敛速度。但在具体实际例子中，找到一个合适的学习速率相对比较困难。所以想要找到一个合适的学习速率，需要不断调整学习速率，对比网络的学习训练时间和网络收敛速度是否满足要求。由于各网络参数的调整都受到统一的学习率影响，这使得在学习训练过程中避免了出现局部极小点。

具体的自适应调整学习率的过程可以简单概述为：先假设一个最初的学习率，对网络进行训练学习，当误差变大时，就会出现网络局部极小点，则需要在学习率上乘以一个小于1的常数l，继续进行训练学习；相反，则需要在学习率上乘以一个大于1的常数g，然后继续训练。对于常数g和l的选取，g一般应略大于1，约为1.05；l与g相比，应小于1，约在0.95左右。g和l之间具有紧密的联系，但必须依据具体的实际情况选取不同的g和l。

4 在地铁隧道变形分析中的应用

利用BP神经网络对某段地铁变形监测数据进行处理，即对SGC01-01监测点的数据进行训练学习和预测。样本数据如表1所示。

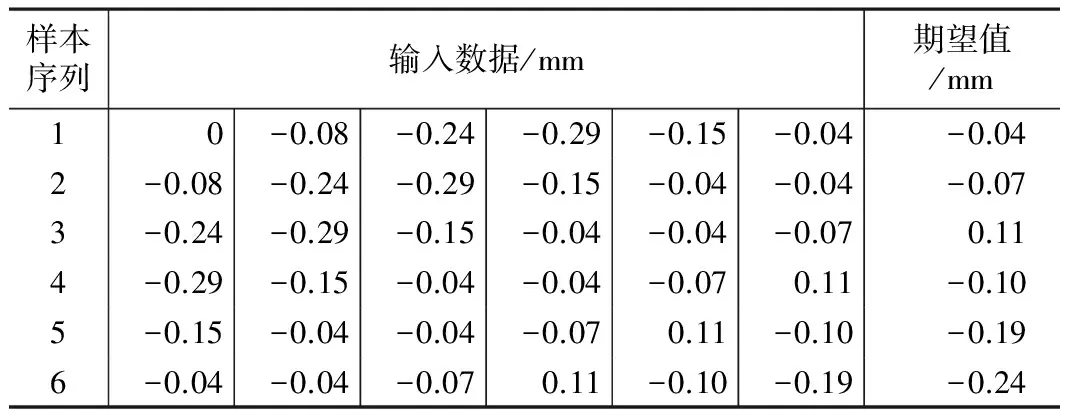
监测点样本数据 表1

续表1

对表1中前30组数据利用BP神经网络模型进行学习训练，通过MATLAB编写的BP神经网络程序，实现结果如表2所示。

训练样本数据 表2

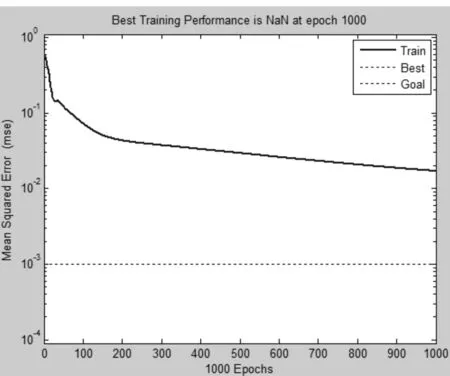
图1 训练样本的误差收敛

利用已经训练好的BP神经网络模型，对31～35样本数据对进行训练预测，预测结果如表3所示。

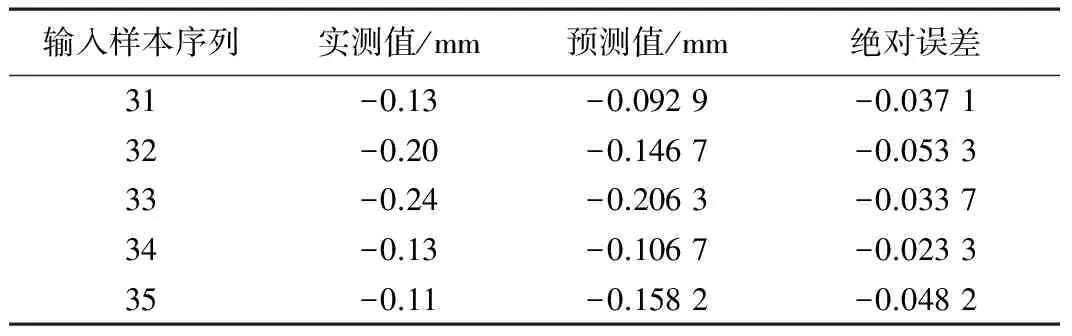
预测结果 表3

应用附加动量法和自适应调整学习率的方法来对BP神经网络算法进行改进，利用这些改进方法再次对BP神经网络模型进行训练，训练结果如表4所示。

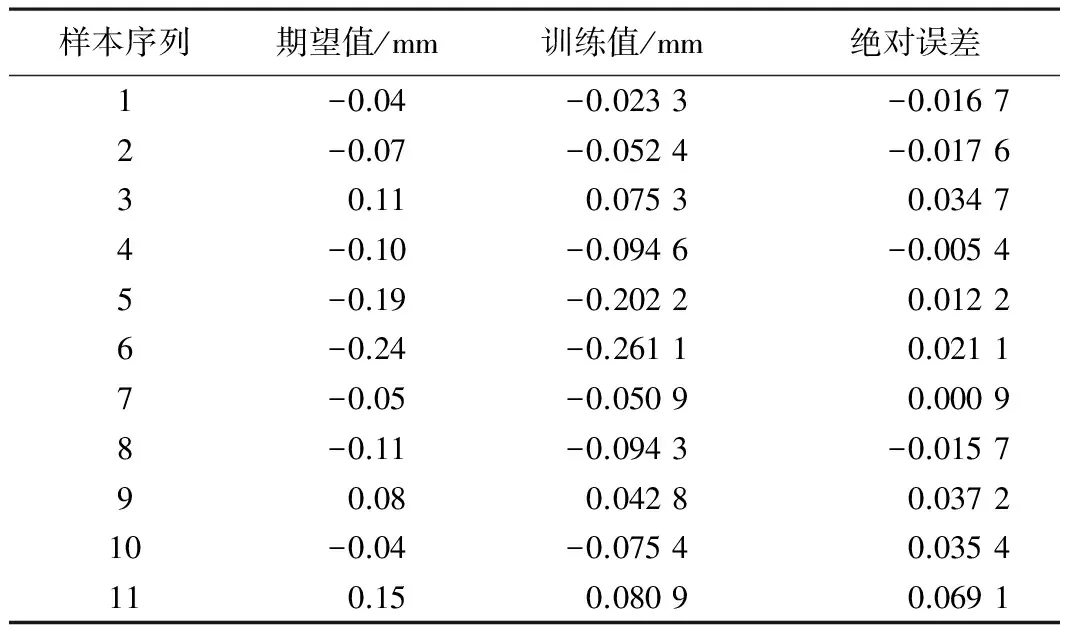
BP神经网络优化模型预测结果 表4

续表4

图2 BP神经网络优化模型收敛图

利用训练好的优化的BP神经网络模型同样对31期～35期数据进行训练预测，预测结果如表5所示。

BP神经网络优化模型预测结果 表5

对两种模型的误差结果做对比，结果如图3所示。

通过利用BP神经网络模型在实例中的应用可以看出，BP神经网络具有非线性映射能力、泛化能力等优点，由于数据经过平差计算，不含有较大误差，所以BP神经网络的容错性优点不能很好的体现。

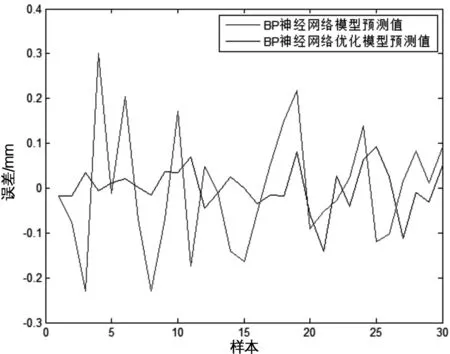
图3 误差结果对比图

通过对比图2和图3可以看出，经过优化的BP神经网络模型的网络收敛速度明显加快；再通过图3可以看出，优化的BP神经网络模型的误差要比BP神经网络模型的误差稳定且基本偏小。因此改进的BP神经网络模型算法能够得到较好的应用。

5 总 结

综上，对比BP神经网络预测模型与改进后的BP神经网络预测模型的预测结果，改进后的BP神经网络模型的网络收敛速度明显快于BP神经网络模型，预测精度要高于BP神经网络模型的预测精度。同时，在数据拟合方面，具有良好的逼近能力，能够有效提升网络的收敛速度，避免陷入局部极小点，可以进行多期数据的预测，能够达到预期的效果。

[1] 黄声享，尹辉，蒋征. 变形监测数据处理(第2版)[M]. 武汉：武汉大学出版社，2012.

[2] 马锐. 人工神经网络原理[M]. 北京：机械出版社，2010.

[3] 王玉雯，陈颖辉，师庭飞. 改进的BP网络在深基坑变形预报中的应用[J]. 科学技术与工程，2010，18(15)：3791～3794.

[4] 刘绍堂，潘国荣. 基于激光扫描的隧道变形监测的误差来源及变形分析[J]. 铁道工程学报，2013(5)：69～74.

[5] 洛成风. 遗传算法优化的BP神经网络城市不透水层百分比估算[J]. 测绘科学，2011，36(1)：48～50.

[6] 刘冠兰. 地铁隧道变形监测关键技术与分析预报方法研究[D]. 武汉：武汉大学，2013.

[7] 刘丹丹. 灰色模型分析法在高层建筑物变形监测预测中的应用[J]. 测绘与空间地理信息，2014，(37)2：203～205.

[8] 严容. 基于小波去噪的BP神经网络在变形预测中的应用[D]. 北京：中国地质大学，2014.

[9] J R Hull. A Neural Network Algorithm using wavelets and Auto Regressive Inputs for System Identification of the 1997[J].IEEE International Conference on Networks，1997，2(4)：724～727.

[10] Zhang Qinghua，Albert Benveniste. Wavelet networks[J]. IEEET rans on Neural Networks，1992，3(6)：889～898.

[11] 周品. MATLAB神经网络设计与应用[M]. 北京：清华大学出版社，2013.

Application of Improved BP Neural Network Model in Tunnel Deformation Analysis

Guo Song，Lu Jinping，Zou Yu

(Jiangxi College of Applied Technology，Ganzhou 341000，China)

In order to overcome the low forecast accuracy and slow convergence of traditional BP neural network model in data fitting，proposed an improved BP neural network method. Using improved model to analysis and forecast a subway tunnel deformation monitoring data，Combined with MATLAB data handler program to achieve comparison of the two models of the same before and after the data processing results，Verify the effectiveness and reliability of the improved model.

deformation monitoring；neural network；BP neural network；MATLAB

1672-8262(2017)01-137-05

P258，TU196

B

2016—07—04 作者简介：郭松(1990—)，男，助教，主要从事工程测量技术的教学与科研工作。 基金项目：江西省教育厅教改立项课题(JXJG-15-52-10)