基于对数灰关联度及IOWGA算子的组合预测方法及应用
2017-03-01胡文权葛文唐旭徐长虹崔逍
胡文权,葛文,唐旭,徐长虹,崔逍
(1.宁波市测绘设计研究院,浙江 宁波 315402; 2.宁波诺丁汉大学,浙江 宁波 315100)
基于对数灰关联度及IOWGA算子的组合预测方法及应用
胡文权1*,葛文1,唐旭2,徐长虹1,崔逍1
(1.宁波市测绘设计研究院,浙江 宁波 315402; 2.宁波诺丁汉大学,浙江 宁波 315100)
针对传统组合模型建模准则单一、权值固定不变的缺陷,引用最优加权组合建模理论,在诱导有序加权几何平均(IOWGA)算子的基础上,结合对数灰关联度,研究了一种改进的IOWGA算子的组合模型。其核心思想是以对数灰关联度为准则,基于单一模型各时刻拟合、预测的精度高低进行有序赋权。文中对优性组合的判定方法及组合模型预测效果评价准则亦进行了研究。将组合模型应用到宁波市某路基沉降预测中,取得了良好的效果,提高了预测精度,验证了模型的有效性。
对数灰关联度;IOWGA算子;组合模型;沉降预测
1 引 言
有序加权平均(OWA)算子是一种集结信息算子,它能有效地集结数据信息。自美国学者Yager提出该算子后,相关研究得到了国内外专家的高度重视。目前,理论研究和实际应用较多的是诱导有序加权几何平均(IOWGA)算子[1]和诱导有序加权调和平均(IOWHA)算子[2]。基于此类算子的组合模型,主要考虑依据单一预测方法在不同时刻的拟合、预测精度进行有序赋权,此种建模方法可以避免因权值不变而导致精度降低、与实际不符等缺陷。
国内外学者研究的组合模型[3]大都以误差平方和最小作为建模准则。近年来,依据相关性指标而建立的组合模型得到了越来越多的应用。本文采用相关性指标对数灰关联度[4]作为优化准则,由此建立的组合模型的预测值更接近实际值,事实证明,用它作为优化准则具有可行性,将其应用到沉降预测中,提高了预测精度,得到了良好的预测结果。
2 基于对数灰关联度的IOWGA算子的组合模型的构建
2.1 IOWGA算子

定义1令
(1)
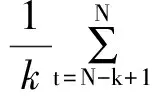
定义2设(
IOWGAw(
(2)

沉降预测中常以预测精度ait作为预测值xit的诱导值并与之组成二维数组

(3)
其中,t=1,2,…,N,则称式(3)为沉降量的组合预测值。IOWGA算子综合考虑了各单一模型精度时高时低的特点,充分利用了其有用信息。
对式(3)两边取对数,得到:

(4)
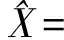
xa-index(it)=lnxt-lnxa-index(it)
(5)
由式(4)和式(5)可得:

(6)
N期总的组合预测对数误差平方和S为:

(7)
因此,基于IOWGA算子的组合预测模型的公式可表示如下:

(8)
根据上述定义的组合预测对数误差信息方阵,上式可简记为:

(9)
其中,R=(1,1,…1)T。据矩阵论相关理论可知,若上述的组合对数误差信息矩阵E为正定矩阵,则上式存在唯一最优解[9]:
L*=E-1R/RTE-1R
(10)
2.2 基于对数灰关联度的IOWGA算子的组合模型
为了进一步挖掘IOWGA算子在组合建模时的优势,本文试图将相关性指标中的对数灰关联度和IOWGA算子相结合,根据大小排序后的单项预测值加权计算组合预测值,实际建模时,以预测精度作为诱导变量且以对数灰关联度作为建模准则,构建一种基于对数灰关联度的IOWGA算子的组合模型。令
(11)
式(11)中,γi为第i种预测方法预测值与实际值对数序列的灰色关联度,γ为组合预测值与实际值对数序列的灰色关联度。上式中的ρ为分辨系数,取值范围为:ρ∈(0,1),通常可取ρ=0.5。
组合预测信息矩阵为:
(12)
由et和上式定义的对数灰关联度定义式,式(11)可改写为:

(13)
分析上式可知对数灰关联度γ可由以权系数L=(l1,l2,…,lm)T为自变量的函数表示,简记为γ(L)。据灰色关联度的相关原理可知,对数灰色关联度γ是判断组合方法有效的重要指标,其值越大表示组合预测方法越有效。对数灰关联度与IOWGA算子相结合的组合模型的组合权值可由下列表达式[10]求出。

(14)
该模型是一个非线性规划模型,利用相关优化软件可以求解各单项预测方法的加权系数。
2.3 最优组合模型

(15)
若γ(L)>γmax,则所组建的模型为优性组合预测,若γ(L)<γmin,则所组建的模型为劣性组合预测,若γmin≤γ(L)≤γmax,则所组建的模型为非劣性组合预测。实际预测中根据上述定义判断组合模型的优劣性。
3 组合预测评价准则
对模型预测效果的评价同样是一项重要的工作。预测精确性主要反映了预测的准确度,实际中常采用以下几种误差评价准则来评定组合预测的精度和准确度[11]。
(1)均方误差(MSE)
(16)
(2)预测误差平方和(SSE)
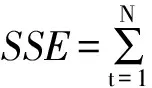
(17)
(3)平均绝对误差(MAE)

(18)
(4)平均绝对百分比误差(MAPE)
(19)
(5)均方百分比误差(MSPE)
(20)
4 实例及分析
某市的一段高速公路于2012年6月建成,为了解其软土路基沉降变化情况,在道路两侧及中间布设沉降监测点。按一定周期监测其沉降量。
本文采用沉降变化显著的监测点作为研究对象,取其初始阶段的19期数据进行拟合、预测,其中选取前15期数据作为模型建立的依据,对后4期数据进行预测并将其与实际监测值对比分析。
分别采用双曲线法及灰色预测法两种单一模型进行拟合、预测。其两种单一模型都是软土路基沉降预测[12]中常用的模型。
双曲线法的表达式:
(21)
式中:S0—原始沉降量(t=0);St—t时刻的沉降量;t—时间间隔;α、β—由实测值求得的系数。由前15期数据可得双曲线模型为:
St=34.48+t/(1.255+0.03t)。据得出的表达式,计算监测点每期的沉降数据。前15期数据拟合值如表1所示,后4期数据预测值如表2所示。
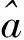
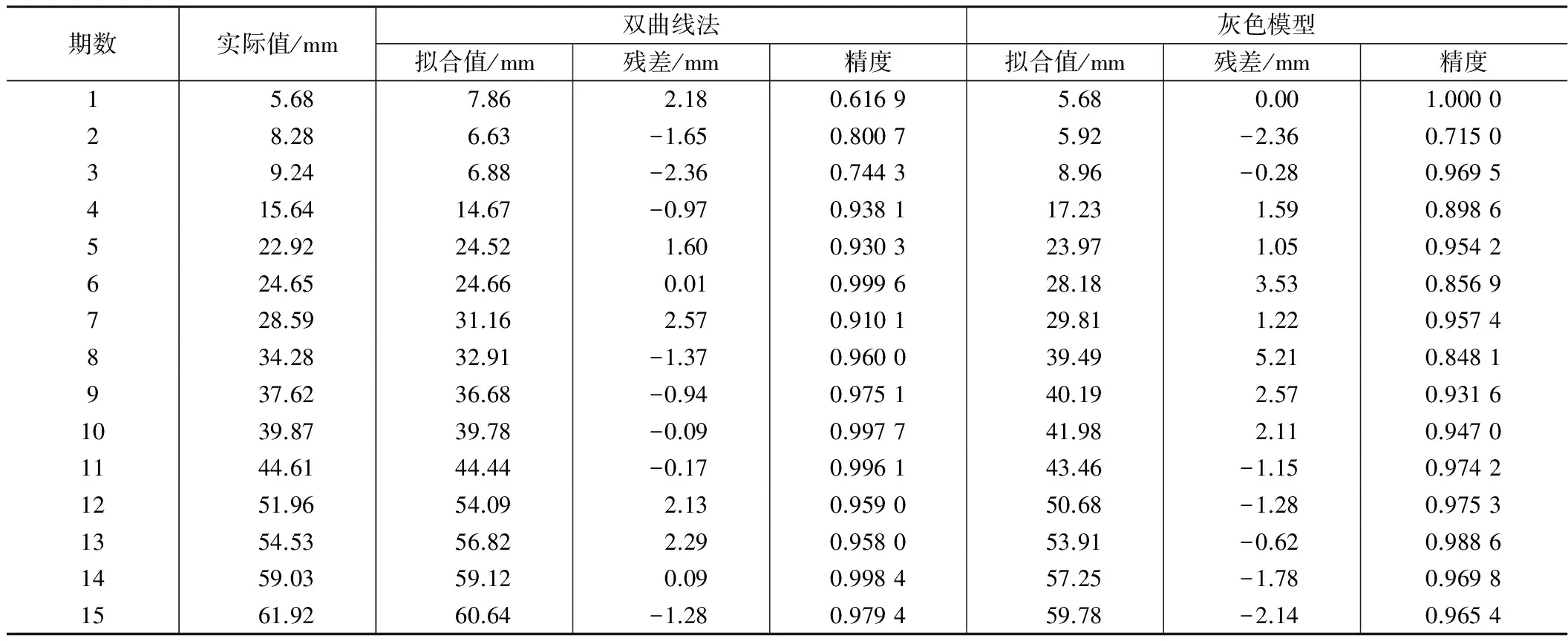
单一模型拟合值与实际值对比 表1

单一模型预测值与实际值对比 表2
根据预测方法的预测精度及对应的预测值可组成二维数组
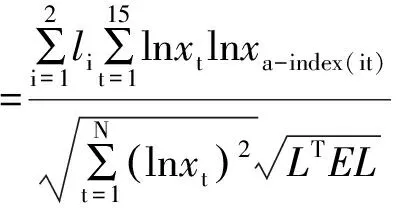
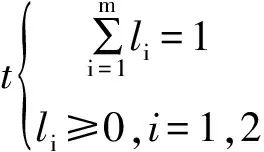
解算上述非线性规划问题,可得:
l1=0.7762,l2=0.2238
表明建立组合模型时,预测精度高的模型权值为 0.776 2,精度低的模型权值为 0.223 8。
由表1和表2的数据结果可知,各单一模型的预测精度时高时低,都包含有用信息,故建立组合模型时,不可依据模型种类赋权,应根据模型各时刻拟合、预测的精度赋权。根据式(3),可得出各时刻组合预测值如表3所示。

组合预测值 表3
根据单一模型及组合模型的残差信息计算各预测模型的精度评价指标值如表4、表5所示。

模型拟合精度评价指标 表4
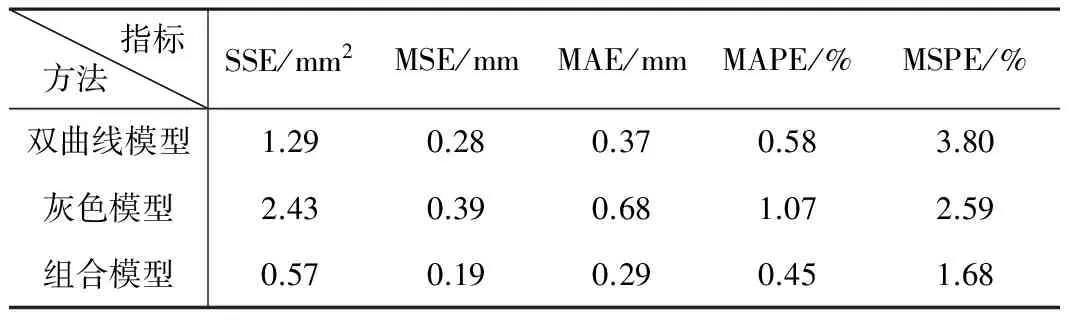
模型预测精度评价指标 表5
根据表1、表2、表3中的数据绘制拟合、预测曲线图如图1所示。
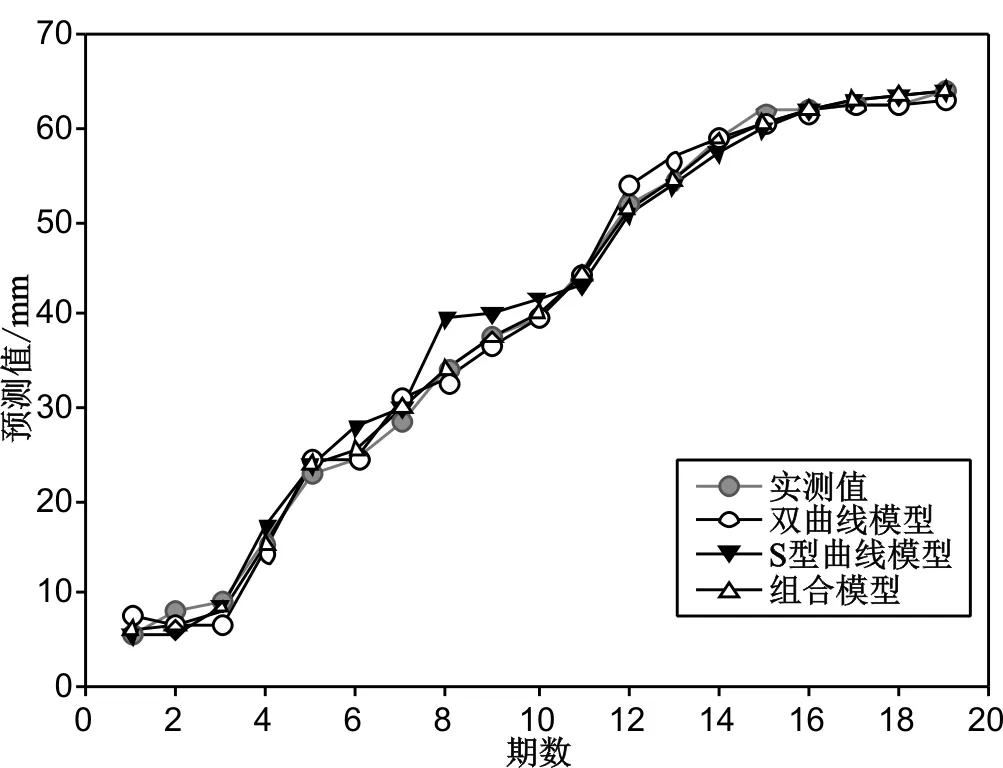
图1 模型预测曲线图
由表1、表2、表3和图1可知,组合模型的预测值更接近实测值,曲线预测趋势与实测值曲线更吻合,更加符合实际情况。由表4、表5模型精度评价值可知,组合模型拟合、预测阶段的误差评价值均小于单一模型,表明组合模型能有效提高预测精度。
单一模型在不同时刻精度有高有低,表明每一个单一模型都包含有沉降量的有用信息。实例表明,基于对数灰关联度及IOWGA算子的组合预测方法,充分考虑到在不同时间节点单一模型预测精度不同的特点,并以对数灰关联度为建模准则,此种建模方法能够有效利用各模型的有用信息。
计算单一模型及组合模型的对数关联度值分别为:γ1=0.882 6,γ2=0.699 1,γIOWGA=0.910 5。由最优组合模型的定义可知,组合模型为优性组合。
5 结 论
(1)基于对数灰关联度及IOWGA算子的组合模型依据各时刻的拟合、预测精度进行有序赋权,克服了传统方法的缺陷,提高了预测精度,有效利用了模型的有用信息。实例证明,由此建立的组合模型的预测值更接近实际值。
(2)对数灰关联度是相关性指标的一种,将它作为优化准则不仅丰富了模型组建方法而且具有可行性。
(3)模型评价准则是组合模型的重要一方面,本文介绍的几种模型评价准则能全面反应模型预测效果的好坏。
(4)由优性判定准则可知,组合模型的对数灰关联度值最大,表明由此建立的组合模型是优性组合模型。
[1] 陈启明,陈华友. 基于IOWGA算子的最优组合预测模型及应用[J]. 统计与决策,2012(3):88~91.
[2] 陈华友,刘春林,盛昭瀚. IOWHA算子及其在组合预测中的应用[J]. 中国管理科学,2004,12(5):35~40.
[3] 谢朋朋,黄腾,刘阳. 变权组合预测模型在大坝沉降监测中的应用[J]. 测绘工程,2015(4).
[4] 陈华友,盛昭瀚,刘春林. 基于向量夹角余弦的组合预测模型的性质研究[J]. 管理科学学报,2006,9(2):1~8.
[5] 赵鑫,杨德宏,秦国玲等. 一种基于IOWGA算子的沉降组合预测方法及其应用[J]. 工程勘察,2015,43(8):87~92.
[6] 陈华友. 组合预测方法有效性理论及其应用[M]. 科学出版社,2008.
[7] 谷川,秦世伟. 基于预测有效度的变形数据组合预测[J]. 大地测量与地球动力学,2008,28(5):73~76.
[8] 周礼刚,赵娟,陈华友等. 基于向量夹角余弦的IOWGA算子组合预测模型[J]. 合肥工业大学学报·自然科学版,2010,33(9):1425~1429.
[9] 王彬. 基于IOWGA算子的组合预测方法及其应用[J]. 西安工程大学学报,2012(1):108~111.
[10] 陈华友,赵佳宝,刘春林. 基于灰色关联度的组合预测模型的性质[J]. 东南大学学报·自然科学版,2004,34(1):130~134.
[11] 马永开,唐小我,杨桂元. 优性组合预测方法存在判别定理[J]. 预测,1995(2):57~58.
[12] 李松,李妍,王柳. 改进IOWHA算子组合预测模型[J]. 计算机工程与应用,2015(3):260~264.
[13] 刘思峰,谢乃明. 灰色系统理论及其应用[M]. 北京:科学出版社,2005.
Based on Combined Forecasting Methods and Application of Gray Association and IOWHA Operators
Hu Weiquan1,Ge Wei1,Tang Xu2,Xu Changhong1,Cui Xiao1
(1.Ningbo Institute of Surveying & Mapping,Ningbo 315042,China; 2.The University of Nottingham Ningbo China,Ningbo 315100,China)
The traditional combination of modeling guidelines for single weights fixed defects,citing the optimal weighted combination of theoretical modeling,the induced ordered weighted geometric mean (IOWGA) operator based on the combination of gray association study a combination of an improved model IOWGA operator. Its core idea is based on gray association guidelines,each time fitting based on a single model,the level of accuracy of prediction orderly empowerment. Excellent article on composition and method for determining the effect of a combination of model predictive evaluation criteria also studied. The combined model is applied to Ningbo City,a subgrade settlement prediction,and achieved good results,to improve the prediction accuracy,to verify the validity of the model.
on the gray association;IOWHA operator;combined model;predict settlement
1672-8262(2017)01-129-06
O221,TU196
A
2016—08—31 作者简介:胡文权(1988—),男,助理工程师,主要从事城市基础测量及数据处理工作。 基金项目:宁波市自然科学基金(2015A610116)
