水运灾害应急资源调度优化策略研究

纪昌杰， 宋庭新

(湖北工业大学机械工程学院， 湖北 武汉 430068)

水运灾害应急资源调度优化策略研究

纪昌杰， 宋庭新

(湖北工业大学机械工程学院， 湖北 武汉 430068)

汉江水上运输量的不断攀升，发生事故概率也越来越高。合理的应急资源调度是汉江水上运输安全的基本保障，及时有效的调度能够明显提高救援的效率与资源的使用率。目前许多资源调度方案优化目标过于单一，因此建立了改进的T-C-Q模型。T-C-Q模型分别以响应时间最短、调度成本最低、资源点的资源品质等级最高作为优化目标，以解决资源优化配置问题。

水运交通； 灾害处置； 资源调度

影响水上运输安全的重要因素是恶劣气象条件，特别是汉江流域经常出现大范围持续雾霾天气，成为水上交通安全管理工作的重点[1]。一个高效的应急资源调度是救援的基本保障，但在实际工作中，汉江的资源调度问题是非线性的规划问题，不能只用一个标准去评判决策方案的优劣，因为各标准之间的关系是复杂的，有的互相依存，有的甚至是相互矛盾的，所以解决这种问题只依靠一个标准的优化手段是不够的。

在许多的应急资源配置模型中，往往只涉及到应急时间、应急成本等一个或多个指标。例如：T模型就是用最少救急时间为优化指标；，而T-C模型则以最少救急时间和最少应急成本为优化指标。本文在分析现有的应急方案的基础上，对上述模型进行改进，建立T-C-Q三指标来进行优化，旨在增强事故的处置能力和救灾的快速反应能力。

1资源调度建模

1.1数学描述

以汉江的某水段发生安全事故，需要救援资源为例，本文拟建立一种多目标组合优化的资源配置模型，先将上述数据进行预处理，根据地理网络图，车道上汽车速度v，船舶速度v1以及汉江的水流速度v2等数据依据Dijkstra算法算出第k(1≤k≤m)个应急资源点到达灾害地点的最短时间tk(tk>0)。通过这一系列计算后，改进的数学描述如下。

汉江的某水段发生了安全事故，它需要的A类救援资源数量为d(d>0)，有m(m≥1)个应急资源点包含有这种资源，第k(1≤k≤m)个应急资源点所包含该资源的品质为qk(qk>0)，这种资源的数量为ak(ak>0)，到达灾害地点的最短时间tk(tk>0)且满足t1≤t2≤…≤tk，用(xk=0或1)来表明该资源点是否被选中，其中0表示未被选中，1表示选中。

1.2T-C-Q模型建立

水运灾害应急资源配置优化问题中不同的决策需求会致使决策有不同的优化标准，所以是含有多个相互冲突的优化标准的非线性规划问题，也就是说需要用一个以上的目标去判断方案的优劣，而这些目标之间往往不那么协调，甚至是相互矛盾的[2]。

一旦灾害事故发生后，能否及时有效将相关资源运送至目的地将对整个救援行动的成败起到决定性的影响，相关资源一定要在最少的时间内运送至指定地点。在实际过程中，应当以最后一个到达指定地点的运输时间作为应急响应时间。所以救急时间

(1)

在现实中，应急成本也是至关重要的，将应急成本最少作为一个优化目标，即

(2)

除了上述两个指标外，资源点的资源品质等级应该被作为优化目标之一。在这一个优化目标的基础上对常见的T和T-C模型进行改进。例如品质较好的吸油毡的吸油能力较强，从不同应急点调度的相同面积的吸油毡就会因为品质的不同而起到不同的效果。很明显，品质较好的吸油毡单位面积吸油能力更强，从而使救急的效率得到提高。所以这里将资源点的资源品质等级最高作为一个指标，即

(3)

确定了相应指标后，资源配置过程中还应该满足一定受到一些约束条件的约束，即

(4)

t1≤t2≤…≤tk

由以上公式可以得到T-C-Q模型

上式中：

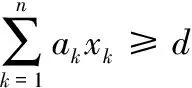
t1≤t2≤…≤tk

(5)

2 T-C-Q模型求解

2.1 多目标处理

在求解多目标优化问题中，一般采取的解决方案有线性组合法、理想点法、乘除法，笔者采用线性组合法来进行优化分析[3]。线性组合法是将各分目标函数用线性组合的方法构成一个新的目标函数(即评价函数)，然后进行求优的方法，也就是将多目标转换为单目标求解。选择一组加权系数w1,w2,…,wp，满足

用fi(x)与wi(i=1,2,…,p)的线性组合构成的评价函数为：

(6)

应急组专家制定方案时，将这3个指标根据重要程度赋予不同的权重，此时可以得到

(7)

其解即为模型的解。

2.2 遗传算法

求解单目标优化问题有许多经典算法，这里选用遗传算法来进行求解。遗传算法是一类借鉴生物界自然选择和自然遗传机制的随机搜索算法，其思想源于达尔文的进化论[4]。

生物遗传的基本单位是染色体。交叉操作是交换两个染色体的片段，变异操作是染色体的某一片段随机发生改变。染色体间通过交叉、变异产生新的染色体，适应性强的染色体存活下来。经过许多代遗传以后，能产生适应度更高的染色体。上述过程用于优化计算，数学上称为人工遗传算法[5]。

2.3 模型求解

2.3.1 初始种群和规模 在变量x的取值范围内随机抽取若干个数，每一个数称作一个染色体，这些数构成一个种群。这里设置种群N=5n，模型中的指标个数为n。

(8)

2.3.4 选择 在遗传中选出个体适应度强的操作叫做选择。本文选用轮盘赌的方式进行选择。轮盘分为N个扇形区域扇区面积与染色体的适应度成正比。

2.3.5 交叉操作 按一定的概率从当前种群中随机选出两个个体，随机确定基因交换位置，交换其中一部分基因，这样就会形成两个新的个体，作为下一代的染色体。交叉概率根据经验一般定为0.8。

2.3.6 变异 使个体基因中某一位以一定概率发生变化，引入适当的扰动，可以避免局部极值，本文选取变异为0.9。

2.3.7 结束条件 将迭代次数作为结束条件，设为100，当触发这个条件时算法终止。

3 应用算例及分析

2015年8月14日，一艘从湖南运送2500 t沙子的机动货船，在汉江硚口区政府附近江面发生漏水，随后侧翻。本文选取此货轮沉没事件的数据进行仿真试验。

假设需要12台多波束设备参与救援，拥有该设备的应急物资存放点处的相关信息见表1，其中包括该应急点处拥有的多波束设备的数量ak，应急点到灾害地点的最短时间tk，应急点中拥有的多波束设备的品质等级qk，取值范围为[1,10]，其中最高级为1，最低等级为10。

表1 应急所需多波束设备配置表

依据表1中的参数，带入上文中的多目标模型中，取初始种群大小，交叉概率，变异概率分别为30，0.8以及0.9，再通过Matlab的遗传工具箱进行计算，如图1所示，输入相应的参数。点击start开始进行计算。

图 1 Matlab遗传算法工具箱

计算的流程如图2所示。

图 2 遗传算法计算流程

在经过了100次的迭代计算后得到适应度最好的解为101010，即选取的应急资源配置地点分别为A(玉峰工业园)、C(华升工业园)、E(汉阳汤山工业园)。

4 结束语

本文对灾害条件下的资源配置过程进行分析，把资源调度问题转换成一个数学问题，在分析了救急时间、救急成本、应急设备品质等级的影响及重要程度之后，建立了灾害条件下资源配置的T-C-Q模型。本文运用线性组合法将多目标的T-C-Q模型构造成单目标函数进行优化，再通过遗传算法来对灾害条件下的资源配置T-C-Q模型进行求解，最后以货轮沉没事件为例来验证灾害条件下的资源配置模型的正确性。灾害条件下的资源调度是一个错综复杂的过程，而本文提出的模型是基于某一种物资进行调度。但水上灾害事件有时发生在多个地点，需要多种物资同时调度。并且，在实际情况下资源调度是一个动态决策的过程，需要考虑资源的消耗情况动态地改变资源需求量，这是今后需要继续研究的问题。

[1] 谢敏. 针对河流水华现象的生态调度研究[D].南京：河海大学,2007.

[2] 曹荣梅. 强拟凹函数的性质及在效用函数中的应用[D].武汉：武汉科技大学,2010.

[3] 齐鹏辉. 基于数据包络分析的水火电力系统多目标决策方法[D].南宁：广西大学,2013.

[4] 王银年. 遗传算法的研究与应用[D].无锡：江南大学,2009.

[5] 赵义红,李正文,何其四. 生物信息处理系统遗传算法探讨[J]. 成都理工大学学报(自然科学版),2004(5):531-534.

[责任编校： 张 众]

Marine Disaster Emergency Resource Scheduling Optimization Strategy Research

JI Changjie，SONG Tingxin

(SchoolofMechanicalEngin.，HubeiUniv.ofTech.，Wuhan430068，China)

In recent years, water transportation accidents caused by meteorological disasters have occurred now and then, which has seriously hindered the development of transportation and national economy, so the corresponding emergency decision system is needed to guide and manage the rescue work for water transport. With the increase of water transportation, the accident probability is becoming higher and higher. Reasonable emergency resource scheduling is the basic guarantee of Hanjiang River water transportation safety, timely and effective scheduling can significantly improve the efficiency of resource use and the rescue rate. At present, the aim of many existing resource scheduling optimization schemes is single, so this paper established the improved T-C-Q model, which takes the shortest response time, the lowest cost, the highest quality resources as the optimization goal, and is used to solve the resource allocation problem.

water transportation, disaster treatment, resources scheduling

2016-12-08

湖北省交通运输厅科技项目(鄂交科教2014-721-4-3)

纪昌杰(1991-)，男，湖北大冶人，湖北工业大学硕士研究生，研究方向为企业信息化

1003-4684(2017)01-0105-04

TP301.6

A