无衍射光莫尔条纹图像处理及计数方法研究

商逸远，吕清花1,，翟中生，成纯富1,，吕辉1,，杨练根,4

(1 湖北工业大学太阳能高效利用湖北省协同创新中心，湖北 武汉 430068;2 湖北工业大学理学院，湖北 武汉 430068; 3 湖北工业大学 机械工程学院，湖北 武汉 430068；4 精密测试技术及仪器国家重点实验室, 天津 300072)

无衍射光莫尔条纹图像处理及计数方法研究

商逸远2，吕清花1,2，翟中生3，成纯富1,2，吕辉1,2，杨练根3,4

(1 湖北工业大学太阳能高效利用湖北省协同创新中心，湖北 武汉 430068;2 湖北工业大学理学院，湖北 武汉 430068; 3 湖北工业大学 机械工程学院，湖北 武汉 430068；4 精密测试技术及仪器国家重点实验室, 天津 300072)

在无衍射光测量中，莫尔条纹的计数准确性将影响测量结果的正确性。在分析无衍射光莫尔条纹特征的基础上，提出利用图像处理方法实现莫尔条纹的精确计数方法。对采集到含有高频干扰的无衍射莫尔条纹，利用图像增强提高对比度，选择合适的低通滤波器消除无衍射光中高频信息及噪声信号，再经过二值化和平滑处理得到轮廓清晰的莫尔条纹，然后利用坐标变换将图像转换到极坐标，根据莫尔条纹灰度值在一周内的突变特性，采用多次间隔扫描法确定条纹数目。实验结果表明，该方法能精确、有效地计算无衍射光莫尔条纹数目。

莫尔条纹； 图像处理； 区域连续扫描法； 无衍射光

无衍射光[1-3]由美国罗切斯特大学的Durnin于1987年首次提出。在工程技术上，无衍射光由于其径向光强分布不随传播距离变化，在光电瞄准跟踪、测量物体表面形貌及多自由度运动误差等方面备受关注[4-6]。莫尔条纹技术[7]具有对位移高倍率放大的光学特性，可对位移量进行准确测量和控制。将无衍射光和莫尔条纹干涉技术相结合，可有效提高测量精度和测量范围，实现大范围几何量的精密测量[8-9]。

文献[8]中利用单束无衍射光与同心圆光栅形成莫尔条纹，虽提高了测量灵敏度，并具有抗激光漂移的优点，但在使用中需要保证轴锥镜产生的无衍射光条纹间距与圆光栅的光栅常数匹配。文献[9]中的莫尔条纹仍需要依靠无衍射光与光栅配合产生，文献[10]提出了一种利用两束无衍射光干涉产生莫尔条纹的计数方法，但仅对仿真的无衍射光莫尔条纹进行了分析，没有实际验证。

无衍射光莫尔条纹技术在测量中有重要的应用前景，但目前对其特性及计数技术的研究较少。本文采用两束无衍射光干涉形成莫尔条纹，对CCD采集到的图像通过背景校正、低通滤波、二值化等预处理过程减少高频噪声和光强不均的影响，再进行极坐标变换，最后采用多次间隔扫描法统计灰度值突变点个数，从而得到条纹的准确数目。

1 无衍射光莫尔条纹原理

图 1 无衍射光莫尔条纹获取装置示意图

在实际应用中，轴锥镜(Axicon)具有稳定的线焦特性，常作为无衍射光产生元件，其产生的无衍射光束横截面光强分布为零阶贝塞尔函数形式[11]。图1所示的光路能产生无衍射光莫尔条纹，且可应用于运动误差的测量。He-Ne激光器发出的平行光经扩束准直镜后入射到轴锥镜中产生无衍射光，到达分光棱镜1后分成两束，一束经反射镜1和分光棱镜2后被CCD接收，另一束光经过反射镜2和分光棱镜2后，也入射到CCD中。这两束无衍射光将干涉并形成莫尔条纹。

对于CCD处接收的无衍射光干涉模型，文献[11]推导出其光强分布近似为

(1)

由式(1)知干涉光强为两个中心位置不同的零阶贝塞尔函数的叠加，两个贝塞尔函数的中心位置由R1和R2决定。图2a给出了图1所示系统的两束无衍射光的干涉结果，从图中可看出清晰的莫尔条纹，且莫尔条纹的数量不受无衍射光的光强分布的影响，因此无衍射光莫尔条纹的原理可以用图2b所示的模型进行近似，将单束无衍射光的贝塞尔函数近似看作周期函数，从而将干涉图像近似看作两块栅距为d的同心环形光栅产生的莫尔条纹，其如图2b中虚线所示。

(a)莫尔条纹实验图像

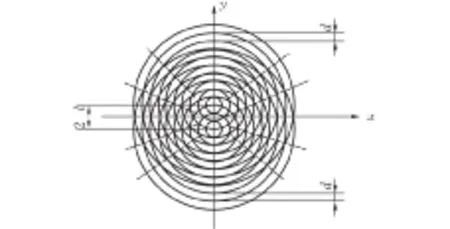
(b)莫尔条纹原理图图 2 无衍射光莫尔条纹图像及原理

将两光栅按m1=0,1,2…，m2=0,1,2，…，由内向外编号，于是两光栅对应的同心圆环的方程为：

x2+(y+Δl)2=R12=m12d2

(3)

(4)

其中：Δl为两光栅圆心偏离坐标原点的距离；d为光栅节距。

两光栅将干涉产生莫尔条纹，实际应用中，常取减莫尔条纹进行分析，根据式(3)、(4)，两光栅产生的减莫尔条纹的方程为

R1-R2=(m1-m2)d=sd

(5)

将式(3)、(4)代入式(5)可得

(6)

可见莫尔条纹的暗条纹轨迹为椭圆族或双曲线族。

图1中，若分光棱镜2和反射镜2放置在工作台上，由于导轨存在水平直线度、俯仰角、偏摆角、滚转角等多个自由度的运动误差，两光斑中心的相对位置将因此发生改变，而产生的莫尔条纹的数量也将发生相应改变，因此利用该装置可以测量多自由度的运动误差。

文献[13]推导出无论两光栅原来的中心距为多少，其中心距每增减栅距d，相应的总莫尔条纹数将增减4，即莫尔条纹的数量变化Δn与两光栅中心距变化Δl的关系为

(7)

如果能够对莫尔条纹进行精确计数，就可得到两中心点的间距，进一步可计算出对应的运动误差，因此莫尔条纹的准确计数是实现图1所示系统运动误差测量精密的前提。

2 无衍射光莫尔条纹图像处理方法

2.1 无衍射光莫尔条纹图像特性及预处理

从图2a实际采集的无衍射光莫尔条纹图像观察到，虽然莫尔条纹比较明显，但条纹对比度不够高，且受单束无衍射光高频条纹和其他噪声的影响，很难直接自动计数。为此，需要对无衍射光莫尔条纹图像进行预处理，主要步骤有：图像增强、频谱分析、低通滤波、二值化和平滑处理等。

为了补偿不均匀的背景亮度带来的影响，增强无衍射光莫尔条纹图像的对比度，利用形态学处理中的顶帽变换[14]，采用合适大小的像素矩阵对图像进行分块开运算，获得背景光强，然后用原图减去背景光强，再通过灰度变换进行校正，以提高对比度。

由于莫尔条纹是由两块空间拍频现象所产生的最低频率含量所组成，因此CCD接收的两束无衍射光的光强分布中空间频率最低(即空间周期最大)的含量构成了莫尔条纹的基波。因而可按傅里叶变换原理把光栅副透射光场分解为不同空间频率的分量，因莫尔条纹的频率比无衍射光本身的频率及叠加产生的其他成分低，选择合适的低通滤波器，则可滤掉高频部分，再经过傅里叶逆变换，则可得到纯莫尔条纹。图2a对应的频谱图如图3所示。

(a)图像频谱的平面图

(b)图像频谱的立体图图 3 图2a对应的频谱图

在达到相同性能指标的情况下，巴特沃斯低通滤波器在通带内拥有最平坦的幅度响应，并对参数量化拥有最低的灵敏度，从而能提高滤波器的稳定性与实用性[15]。根据图3所示的频谱特性，再利用双线性变换法[16]选择通带截止频率为15，阻带截止频率为45，通带衰减的最大值Rp为1 dB，阻带衰减的最小值As为20 dB,计算所需的滤波阶次和截止频率。计算得到最佳设计参数为滤波阶次N=4,截止频率fc=19。为了证明该滤波器的有效性，对图4a(与图2a为同一图像)进行增强后的图像(图4

为了进一步提取莫尔条纹信息，需要对图像进行二值化处理来得到图像轮廓。二值化方法的选取将直接影响图像处理质量。为了保证莫尔条纹的清晰完整，将二值化阈值设为莫尔条纹区域像素点的灰度平均值。令二值化阈值为T，灰度Ci出现的次数为Ni,其中灰度Ci的取值为有限集{0,1,2,…,255}, 则灰度Ci出现的概率

(8)

则阈值

(9)

将式(8)带入式(9)可得

(10)

通过式(10)计算得到的二值化阈值T=116.33，分割后的图像如图4d所示。

经过低通滤波及二值化处理, 靠近图像中心的高频信息被滤掉，条纹的整体轮廓已经比较明显，但图像中还存在少许杂点，且平滑程度不佳。采用均值滤波并结合形态学中的腐蚀、膨胀运算，修补空洞，平滑图像边缘，结果如图4e所示。

图 4 图像预处理过程

2.2 基于坐标变换的莫尔条纹提取算法

考虑到莫尔条纹信号呈辐射状分布，对应的灰度值在一个圆周上具有周期性变化的特点，采用极坐标变换进行处理。根据直角坐标与极坐标的转换关系，有

(11)

其中(x0,y0)为极坐标原点，经过图像增强和滤波等处理，二值化后的图像已经比较均匀，可以图像重心作为极坐标原点使用。令xi,yi,Ci分别为图像中任意像素点的横纵坐标和其对应的灰度值,则重心坐标(x0,y0)可表示为

(12)

根据式(12)求出的重心坐标(x0,y0)，计算结果如图5所示，中心的十字代表了图像重心位置。根据式(11)将图像中每个像素点的坐标(x,y)转换成极坐标中的(r,θ)，通过坐标转换，可以将莫尔条纹图像以极坐标原点为中心进行展开，处理结果如图6所示。

小学语文课堂教学中合作学习效果的提升，最基础的工作是要保证合作学习目标确立的合理性，使这一工作可以有的放矢。通常情况下，根据新课程的要求和现代化教育理念的指导思想，合作学习的目标应该是培养学生的语文学习兴趣、增强学生的自信心、使学生具有集体荣誉感、提升其交流合作能力等等。除此以外，还要使学生通过合作学习来拓展思维，取长补短，实现自我提升。因此，教师要了解合作学习，合理确定合作学习的目标，并能够对合作学习效果进行合理评价，然后分析每个学生、每个团队存在的不足之处，针对性改进，提高教学效果。

图 5 求出重心后的图像

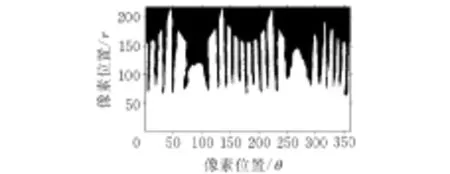
图 6 坐标变换后的图像

由于图像经过二值化处理，莫尔条纹部分的灰度值为1，背景灰度值为0，在该极坐标中画任意一条水平直线，当直线上的点经过条纹与背景的分界点时，相邻两点的灰度值会存在突变，那么每2个突变点就代表1根莫尔条纹的存在，即莫尔条纹数n与突变点个数q之间的关系为：

n=q/2

(13)

为了精确计数莫尔条纹，需要得到准确的突变点个数，只取单一直线进行统计显然不可靠。为了提高准确性和可靠性，本文采用多次间隔扫描法，得到多组突变点的个数，取其出现次数最多的一组。对此，需要定义合适的扫描区间r，在这一区间内用连续多组直线进行扫描。

由于该图像已经过二值化处理，每个像素的灰度值经归一化后只能为0和1，将极坐标下图像每一列的灰度值相加，得到一个一维数组

(14)

其中：Lij表示位于图像的第i行，第j列的元素的灰度值。

该一维数组中纵坐标即对应灰度值为1的像素个数，可看作图像在极坐标中任意位置的长度，则曲线S即为极坐标下的图像轮廓。当莫尔条纹图像占整个图像的比例较小，距离图像边界尚有富余的情况下，可将扫描区间定为曲线的最低点与最高点之间，即

r=[Smin,Smax]

(15)

当莫尔条纹占据整个图像较大面积(图7)时，选取的莫尔条纹图像为矩形，经过极坐标变换后必然使得对角线方向的条纹长度更长，而沿横、纵向的条纹长度相对短些，若仍以式(15)确定扫描区间，会因为不同方向的条纹长短不一而取到多组无意义的突变点，可将扫描区间的上限改为莫尔条纹图像的中心到图像7四边距离的最小值，则可使整个扫描区域基本位于扫描全部莫尔条纹的有效区域内。即

r=[Smin,min(L1,L2,L3,L4)]

(16)

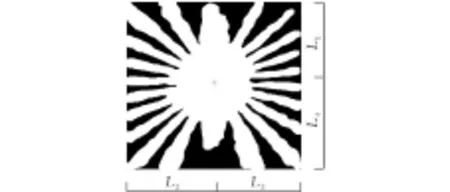
图 7 图像中心到四边的距离

实际处理过程中，上述两种情况都有可能出现，扫描区间取式(15)和式(16)中较小的一个即可。在扫描过程中，若相邻两突变点的间距过小，则认为是条纹边缘不平滑造成的误差，不记录该点。全部直线扫描结束后，统计出现次数最多的一组突变点数量，根据式(13)计算莫尔条纹数目。

3 实验结果

根据以上的理论分析，对图4e处理后的图像进行条纹计数，计算出其中心为(157,145)，选取的扫描区间为[65,156]，如图8a所示，统计出现次数最多的突变点为44,根据式(13)计算出条纹数为22条,与原图像的条纹数量相符。

(a)扫描区域

(b)扫描结果图 8 扫描过程

为了进一步验证该方法的有效性，对图1所示的系统进行实验。采用的光源为波长632.8nm的氦氖激光器，轴锥镜半径为12.5mm,锥角约为0.008rad,采用的CCD相机分辨率为1280×1024，像元尺寸为5.2μm，采集了工作台在3个不同位置的莫尔条纹图像。表1给出了利用上述方法，计算出条纹数分别为8,10,10。

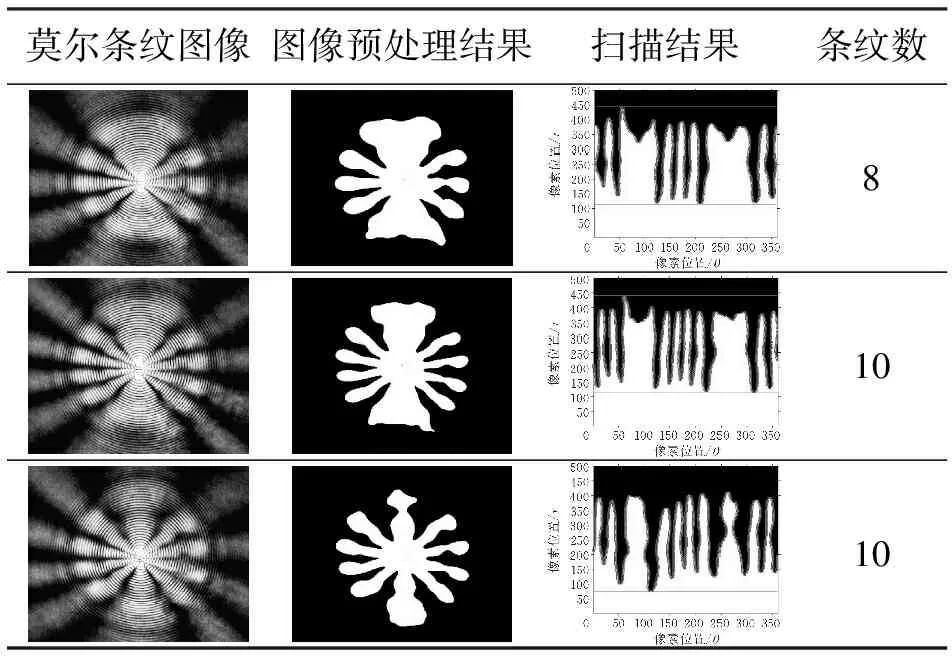
表1 实验图像处理结果

4 结论

根据无衍射光干涉理论，分析了无衍射光莫尔条纹的特点，运用数字图像处理技术,基于CCD采集的莫尔条纹图像，通过图像增强、低通滤波、二值化、坐标变换、多次间隔扫描等处理手段，统计出了无衍射光莫尔条纹的数目。该算法快速有效，计算精确，方法可靠。

[1]DurninJ.Exactsolutionsfornondiffractingbeams(I):Thescalartheory[J].JOptSocAm(A),1987(4):651-654.

[2]DurninJ.Diffractive-freebeams[J].Phys.Rev.Lett.,1987(58):1479-1501.

[3] 邢笑雪,吴逢铁,张建荣.无衍射J0光束的理论分析[J].华侨大学学报(自然科学版),2006,27(1):31-34.

[4] 王中宇,周聪,张朵.无衍射光技术在瞄准系统中的理论与原理实验[J].北京航空航天大学学报,2006,32(11):1337-1340.

[5] 王中宇,王倩,孟浩,王雪.基于无衍射光的表面粗糙度三角测量及其灰色评定方法[J].应用光学,2011,32(5):909-912.

[6]Zhaietal.Measurementoffour-degree-of-freedomerrormotionsbasedonnon-diffractingbeam[J].OpticsCommunications,2016,366:168-173.

[7] 何春娟,刘绒霞,曹磊.莫尔条纹技术在微小位移测量中的应用[J].西安工业学院学报,2005,25(6):565-567.

[8] 赵斌.无衍射光莫尔条纹空间直线度测量的原理与实验[J].计量学报,2001,23(2):81-86.

[9] 赵斌,李虎.长距离无衍射光莫尔条纹直线度测量系统的工作原理[J].光学仪器,2002,24(6):3-6.

[10] 翟中生,严昌文,吕清花等. 一种无衍射光莫尔条纹的计数方法[J].湖北工业大学学报,2015,30(4):1-4.

[11] 翟中生,赵斌.无衍射光束中心光斑的特性研究[J].激光技术,2008,32(5):480-483.

[12] 翟中生,赵斌.无衍射光的干涉实验与理论分析[J].光学学报,2007,27(8):1503-1507.

[13] 黄恩令,姚久胜.同心环形光栅莫尔条纹的机理[J].光电子·激光,1992,3(4):193-200.

[14]RafaelC.Gonzalez,RichardE.Woods,StevenL.Eddins,等. 数字图像处理(MATLAB版)[M]. 阮秋琦,译.北京：电子工业出版社, 2013.

[15] 程佩青.数字信号处理教程(第四版)[M].北京：清华大学出版社，2013:351-368.

[16]LiuFengju,WuJiantong,LiuLi.IIRdigitalfilterdesignbasedonthebilineartransformationandmatlabsimulation[J].AutomationtechnologyandApplication,2008,27(9):44-47.

[责任编校： 张 众]

Research on Image Processing and Counting Method of Non-diffracting Moiré Fringes

SHANG Yiyuan2,LV Qinghua1,2,ZHAI Zhongsheng3,CHENG Chunfu1,2,LV Hui1,2,YANG Liangen3,4

(1HubeiCollaborativeInnovationCenterforHigh-efficientUtilizationofSolarEnergy，HubeiUniv.ofTech.,Wuhan, 430068,China; 2SchoolofScience,HubeiUniv.ofTech.,Wuhan, 430068,China; 3SchoolofMechanicalEngin.,HubeiUniv.ofTech.,Wuhan430068,China; 4StateKeyLaboratoryofPrecisionMeasuringTech.andInstruments,Tianjin300072,China)

The counting accuracy of moiré fringes will affect the accuracy of the measurement results in non-diffracting optical measurement.On the basis of analyzing the characteristics of non-diffracting moiré fringes,an accurate counting method of moiré fringes is proposed with imaging processing.By image enhancement,image contrast is progressed,and low-pass filtering is also applied to eliminate high frequency components and noise of the image.Substantially,clear contour of moiré fringes can be obtained by binarization and smoothing process.After the transformation of the image to polar coordinate,the number of moiré fringes can be counted by multiple interval scanning method from the gray value alternation of moiré fringe image in a circle.The experimental results show that this method is accurate in counting moiré fringes.

Moiré fringe; image processing; interval continuous scanning method; non-diffracting beams

2016-11-17

国家自然科学基金(51405143，51575164，61475044)， 重点实验室基金(PIL1602)，太阳能高效利用湖北省创新协同中心开放基金项目(HBSKFZD2014007)，湖北省大学生创新创业项目(201510500023)

商逸远(1991-)， 男， 湖北武汉人，湖北工业大学硕士研究生，研究方向为光学测量

吕清花(1980-)，女，湖北咸宁人，湖北工业大学讲师，研究方向为光电检测

1003-4684(2017)01-0072-05

O436； TP391

A