基于改进Blocking策略的模型预测控制技术

潘 健， 刘昌龙

(湖北工业大学电气与电子工程学院， 湖北 武汉 430068)

基于改进Blocking策略的模型预测控制技术

潘 健， 刘昌龙

(湖北工业大学电气与电子工程学院， 湖北 武汉 430068)

针对模型预测控制(MPC)在线优化计算复杂的缺陷，在采用输入分块(Input blocking)策略对输入序列 进行固定分块的基础上，，提出了一种移动分块(Move blocking)策略，通过变化的blocking矩阵降低控制量的自由度，从而有效降低模型预测控制在线优化过程中的计算复杂度。同时能够在满足约束条件下保证系统输出紧密跟踪期望值。以四旋翼无人机系统为控制对象，在构建模型基础上，仿真验证了该算法的有效性。

MPC； 移动分块； 计算复杂度

预测控制对于非线性不确定系统有出色的控制效果，可以方便地处理实际系统的各种约束，目前已广泛应用到复杂的工业环境[1-3]。但由于它采用了滚动进行的在线优化，在每一个时刻都需要求解一个有约束的优化问题，因而计算量较大，严重限制了其应用的领域。

国内外学者对如何降低预测控制在线计算复杂度进行了研究，一般是从减少优化变量自由度的角度提出，在文献[4]中称为输入参数化。文献[5,6]提出了两种滚动优化的Input blocking策略，一种是“近精确、远粗略”的水平分块策略，另一种是“长时段粗优化、短时段细优化”的分层分块策略。文献[7]提出了预测函数控制(PFC)，即采用特定函数族(或称基函数)的线性组合来表示当前时刻的最优控制序列，控制量的自由度由基函数的数量决定。文献[8]提出了输入幅值衰减的控制策略，即把当前时刻的最优控制序列近似为固定衰减系数的衰减序列，也可以有效降低控制量自由度。但这些策略由于采用固定的分块方法，优化性能一般会有所下降。

Input blocking策略在优化过程中将输入块中的控制量保持不变，代替了理应变化的控制量，会造成实际输出不能紧密跟踪期望值，针对这一问题提出了一种移动分块策略。该策略通过选定一组block矩阵，实现在不同时刻对控制量进行循环分块，这样预测的未来时刻最优控制序列不会在某一固定区间总保持为常值，可以有效降低固定分块造成的问题。并基于四旋翼无人机控制系统验证了该算法的有效性。

1 有约束MPC的问题描述

(1)

矩阵形式描述如下：

(2)

其中，A是由单位阶跃响应系数ai组成的动态矩阵

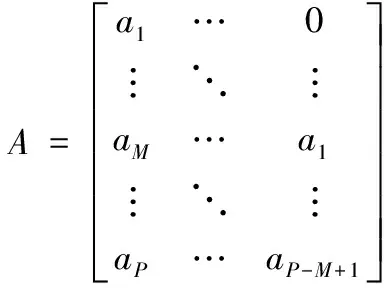
在实际应用中，因物理因素或安全性考量，控制量、输出量和某些中间变量的取值只能限定在一定范围内。假设考虑控制量和输出量的约束：

umin≤u≤umax,ymin≤y≤ymax

在预测控制的滚动优化中，每一时刻的优化都涉及到各控制量在未来M个时刻的增量以及各输出量在未来P个时刻的预测值。这些控制量均应满足给定的约束条件，即

将上述不等式表示为

Δumin≤BΔuM(k)≤Δumax

其中，

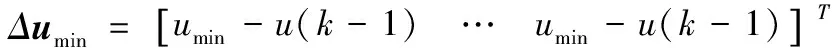
同样，各输出预测值均应满足约束条件，写成向量形式

对于控制量和输出量的约束可以归结为如下形式的对于控制量的不等式约束

CΔuM(k)≤l

(3)

其中C,l均是k时刻已知的量：

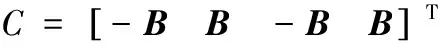
因此根据式(2)、(3)优化性能指标可以写为

CΔuM(k)≤l

(4)

其中，w为参考轨迹；Q，R分别为误差权矩阵可控制权矩阵。

由于式(4)具有二次型性能指标且带不等式约束的优化问题，是一个二次规划问题。QP的标准问题可表示为

s.t.Bx≤d

其中，H为对称正定阵，x为优化变量。

式(4)给出的预测控制优化性能指标可转化为标准QP问题，如下式：

式中，第一项为k时刻的已知项，与优化无关，可从性能指标中除去。进一步记为

即转化为标准QP问题，可用MATLAB优化工具箱中的二次规划函数quadprog得出最优解。

2 Move-blocking策略的应用

针对上述问题，在Inputblocking基础上加入move的思想，即blocking矩阵不再是固定不变，而是一个循环的矩阵组，这样控制器变为动态的控制器。由于封锁的时间步是移动的，如此可以保证系统稳定性，同时也可以降低计算量。

blocking矩阵的选取要满足：1)每行有一个非零元素为1，该行其他元素为0；2)用j*(i)={j|Bi,j=1}表示第i行非零元所在列的序号j，j*(i+1)≥j*(i),i=1,…,M。3)选取blocking矩阵时要保证各分块矩阵的分块数相等，且各分块按矩阵序号依次循环移动。

以一个4维控制量为例，采用Moveblocking策略使其自由度降为3，blocking矩阵组选取为：

则优化性能指标变为

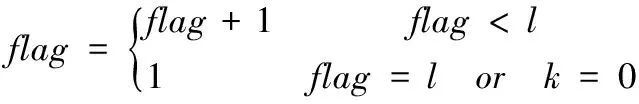
式中flag为blocking矩阵序号，

是降维后的控制量，l是降维后控制量的自由度。

3 算例分析

3.1 四旋翼无人机模型构建

本文研究对象为Quanser公司Qball-X4四旋翼无人机，其数学模型在文[9]中已经给出。其简化后的线性模型为：

其中x,y,z为无人机在地面坐标系下的位移，θ，φ，ψ分别为无人机的倾斜角，滚转角，偏航角；L是无人机重心到四个螺旋桨中心的距离；Jroll,Jpitch,Jyaw为无人机绕x,y,z三个轴旋转的转动惯量；Fi,i=1,2,3,4为对应电机拉力，为了表述方便，将Ui,i=1,2,3,4定义为：

四旋翼无人机的推动器采用无刷直流电机。电机输入电压u与螺旋桨升力F的关系为：

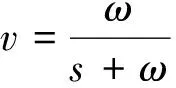
Qball-X4四旋翼无人机参数[9]：K，120N；ω，15r/s；Jroll，0.03kg·m2；L，0.2m；Jpitch，0.03kg·m2；Jyaw，0.04kg·.m2；M，1.4kg。

3.2 系统仿真

(4)

(5)

将表1参数代入(4)、(57)得到系数矩阵：

设定MPC姿态控制器的优化时域P为20，控制域M为5。输出加权R与控制加权Q分别为1、200。选取的blocking矩阵组为：

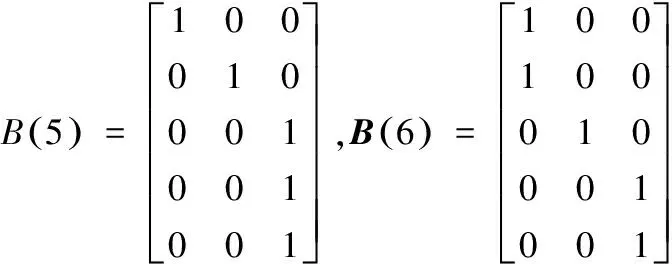
矩阵组选取的思路如图1，通过选定的blocking矩阵可以使控制量的自由度降为3。

图 1 blocking矩阵组

本次研究通过MATLABR2013a仿真比较了MPC(M=5)，MPC(M=3)，Moveblocking-MPC(MB)三种情况下四旋翼无人机姿态控制器阶跃响应的计算时间。实验是在同一台电脑上进行，分别记录10次运算时间并求平均值(单位s)(表1)。

表1 三种情况下的计算时间对比

定义衰减比(Decayratio)为相对MPC计算时间加快的部分比上MPC计算所用时间：

Decayratio=(timeblocking-timeMPC)/timeMPC

根据表1可计算出MB的衰减比为19.24%，且控制域M为5时Moveblocking-MPC的运算量与控制域M为3时普通MPC的计算量相当，实验表明：使用Moveblocking策略可降低MPC算法在线优化的运算量。图2为控制域M为5时Moveblocking-MPC和MPC姿态控制器的阶跃响应对比，图3为控制域M为5时的Moveblocking-MPC和控制域M为3时的MPC姿态控制器阶跃响应对比，表2为俯仰通道阶跃响应仿真结果表。

图 2 MB(M=5)与MPC(M=5)的阶跃响应

图 3 MB(M=5)与MPC(M=3)的阶跃响应

超调量%上升时间/s稳定时间/sMB(M=5)0．21．71．9MPC(M=5)0．21．61．9MPC(M=3)03．13．1

从表2可以看出，控制域M为5时Moveblocking-MPC和传统MPC姿态控制器的阶跃响应控制效果基本相同，即使用Moveblocking策略在降低运算量时并不影响控制效果。且控制域M为5时的Moveblocking-MPC和控制域M为3时的传统MPC虽然运算量相当，但前者的控制效果明显优于后者。

4 结论

在线优化计算量大的问题一直是模型预测控制技术在实际应用中最大的障碍。本文在输入分块基础上提出了一种移动分块策略，通过变化的分块矩阵降低控制量的自由度，从而有效降低模型预测控制在线优化过程中的计算量，同时使系统输出紧密跟踪期望值。本文仿真算例证明了该算法的有效性，其计算量对比传统MPC有明显降低且控制效果基本不变。

[1] 席裕庚. 预测控制[M]. 北京:国防科技出版社,1993:1-10.

[2] 李书臣, 徐心和, 李平. 预测控制算法综述[J]. 系统仿真学报,2004(6).

[3] 席裕庚, 李德伟, 林姝. 模型预测控制-现状与挑战[J]. 自动化学报,2013,39(3):222-236.

[4]QinSJ,BadgwellTA.Asurveyofindustrialmodelpredictivecontroltechnology[J].ControlEngineeringPractice,2003,11(7):733-764.

[5]RikerNL.Useofquadraticprogrammingforconstrainedinternalmodelcontrol[J].I&ECProcessDes.Dev.,1985,24(4):925-936.

[6]LiuL,LiuZ,ZhangJ.LMI-basedmodelpredictivecontrolforunderactuatedsurfacevesselswithinputconstraints[J].Abstract&AppliedAnalysis, 2014, 2014(5):1-9.

[7]RichaletJ,O'DonovanD.PredictiveFunctionalControl[M].London:Springer, 2009.

[8] 杜晓宁, 席裕庚. 预测控制优化变量的集结策略[J]. 控制与决策,2002,17(5):563-566.

[9]RatanasawanyaC,MehrandezhM,ParanjapeR.Nonlinearreal-timeposeestimationofquadrotorUAV[M]//NonlinearApproachesinEngineeringApplications.NewYork:Springer,2012:393-419.

[责任编校： 张岩芳]

Model Predictive Control Strategy Based on Improved Blocking Technology

PAN Jian， LIU Changlong

(SchoolofElectronicandElectricalEngin.,HubeiUniv.ofTech.,Wuhan430068,China)

In order to deal with the computational burden of optimal control, it is common practice to reduce the degrees of freedom by fixing the input. This paper introduces a novel blocking scheme, a move blocking strategy where the blocked inputs are changed to reduce the degree of freedom of control. This paper takes a quadrotor as the subject of the research and structures the mathematics model. Finally, the validity of the new algorithm is verified by computer simulation.

Model Predictive Control; move blocking; computational burden

2015-12-03

潘 健(1962-)， 男，上海人，湖北工业大学副教授，研究方向为电力电子

1003-4684(2017)01-0051-05

TP273

A