一种基于局部多项式回归的气敏传感器模型优化算法
2017-03-01周长林钊守国王振义梁臻鹤
周长林 钊守国 王振义 刘 统 梁臻鹤
(解放军信息工程大学 河南 郑州 450001)
一种基于局部多项式回归的气敏传感器模型优化算法
周长林 钊守国 王振义 刘 统 梁臻鹤
(解放军信息工程大学 河南 郑州 450001)
气敏传感器精确建模,为实现气体精确测量发挥重要作用。针对气敏传感器差异造成自动化系统不稳定问题,提出一种参数校准算法。然后基于改进PSO-BP神经网络拟合传感器响应值与气体浓度之间的关系特性,构建出二维气敏特性模型。同时为减少温度对数学模型影响,又提出回归分析三维模型优化方法。实验及应用结果表明,该参数校准方法以及模型优化方法,提高原模型参数精度以及系统可靠度,为气敏传感器制备与应用提供较高参考价值。
气敏传感器 智能算法 参数校准 温度补偿
0 引 言
随着大气环境日趋恶化,为实现对空气有效监控,对于传感技术的要求也日益提高。气敏传感器以低成本,高灵敏性,高稳定性,高适应性,以及可选择性等优秀特点备受社会青睐,被广泛应用于环境质量监测、空气净化以及空气指标量化等自动化测量系统[1]。但是由于气敏传感器的生产受烧结温度、微结构、表面缺陷、以及半导体氧化物表面修饰掺杂贵金属等条件的影响,只要制备工艺条件稍有不同,往往生产出的传感器响应结果也会产生较大差异[2]。另外气敏传感器易受温度,湿度等条件因素影响,可能会导致自动化系统测量数值发生偏移现象,系统稳定性下降,选择性指标不理想等一系列问题。
自动化测量系统中,解决上述问题的方案主要是以下两种:第一,通过研究制备原理,改善制备工艺,改进产品构造等方式以增强气敏性能,但实现难度较大,且很难克服工艺所带来误差[2];第二,运用软件编程措施对模型参数非线性校准或补偿,关键问题是精确建立数学模型,以降低系统输出漂移[3-4]。目前,国内外许多文献对多种传感器模型优化方法进行研究,但模型优化方法局限性较强,建模精度不高,在气敏传感器建模方面尚未有有效的解决方案。张琦等[5]提出基于线性化参数模型的三轴磁场传感器校准方法,唐炜等[4]就如何构建一个基于温度补偿的传感器模型方法进行了探讨,但不能在复杂性较强的非线性气敏特性模型参数校准中实现,且计算量大。文献[6-8]将智能算法建模的思想应用于非线性系统中,解决复杂非线性化问题,但由于神经网络算法对权重非常敏感,使得每次训练产生结果不同, 俞阿龙等[9]将神经网络与遗传算法结合克服上述不足,但收敛速度较慢。王聪等[10]提出基于确定学习与基于数据的模型优化方法,崔远慧等[3]研究了一个气体传感器的动态高精度测试系统,较好预测了系统的气敏传感器响应,但对于因素补偿问题未考虑,并不能提高传感器的精度。
本文重点阐述气敏传感器响应特性,应用改进粒子群算法-BP神经网络算法数学建模, 对模型定量分析,运用算法校准参数,然后基于局部多项式回归曲面拟合方法,建立温度补偿三维数学模型。本文提出的校准与补偿方法可解决气敏传感器如何精确建模问题,为自动化气体检测设备与控制系统输出响应稳定性问题提供可行的解决方案,为工业生产与产品应用提供更精确的理论依据。
1 参数修正数学模型优化方法
1.1 建模原理分析
气敏传感器测量机理是利用材料表面吸附控制原制,让半导体氧化物与特定气体在一定温度下发生气-固化学反应,引起气敏材料电导变化[2,11]。通过检测电导的响应变化,实现对气体的有效测量。另外半导体敏感材料在不同的气氛下烧结而成的气敏传感器,通常响应结果会大不相同,因此要准确测量气体含量,需要进行实时的数据处理,来建立较为精准的传感器响应特性与气体浓度的数学模型。而模型参数修正和因素补偿是关键[11]。灵敏度是衡量气敏性能的重要参数指标,气敏传感器响应通常用灵敏度系数S来表示,是由传感器在空气中基准阻值以及在某气体中的阻值共同决定。
(1)
式中,RQ(air)为气敏传感器在空气中基准阻值,RQ为传感器的实际阻值。要获取传感器灵敏度系数,通常需要先构建硬件测量网络(实验电路如图1所示),然后测量网络中负载的电压信号,经函数转换公式,得到传感器响应阻值[12]。
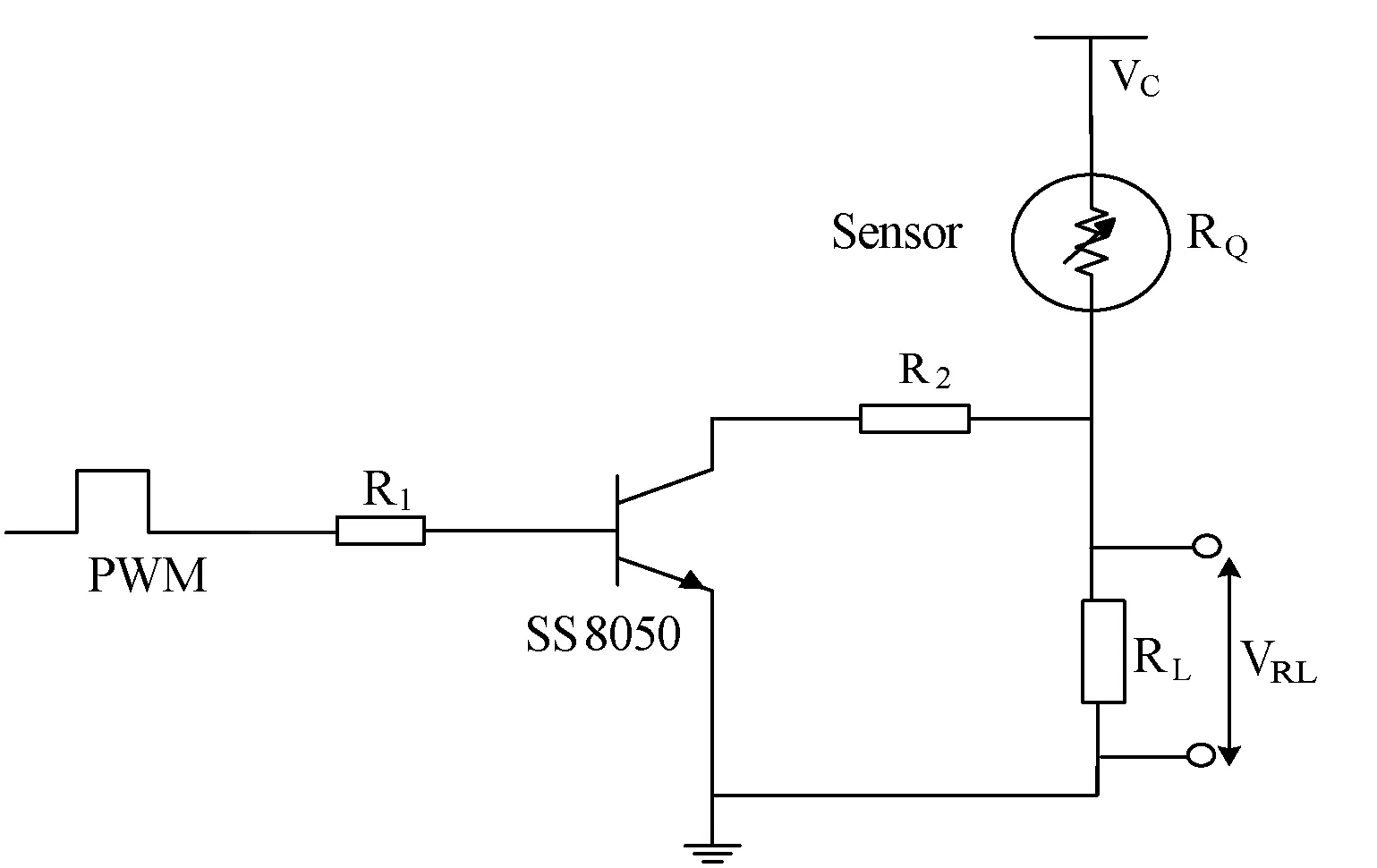
图1 传感器测试电路
1.2 响应信号参数修准方法
(1) 参数校准是基于传感器响应幅值作为函数变量进行的,首先需要判定传感器响应信号状态,排除随机误差对传感器测试结果的影响。计算测量标准差与测量不确定度,并对两者进行比较。
(2)
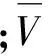
(2) 系统响应信号双参校准。超差状态下,修正传感器系统误差,一般运用归一化修正因子插值修正,分别对气体浓度与电压幅值进行双参校准。
(4)
式中,Mi为测量值(除掉粗大误差),S为国家标定仪器激励信号量值。
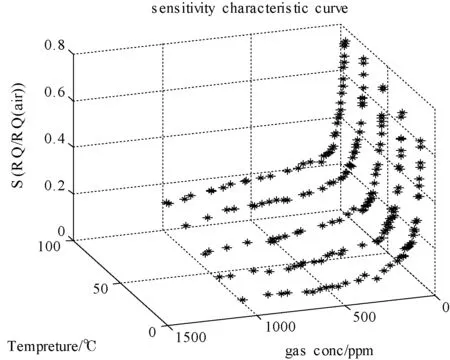
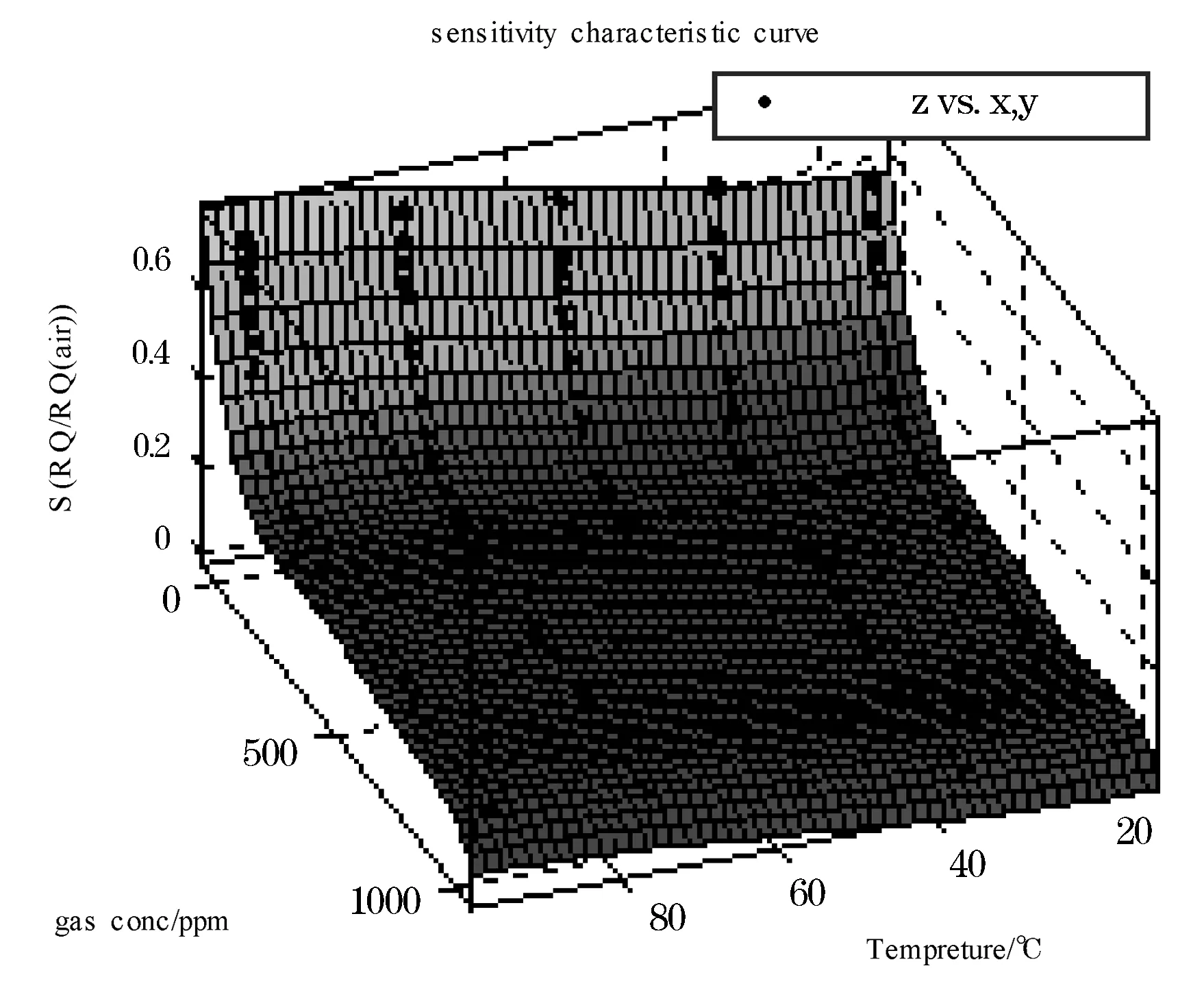
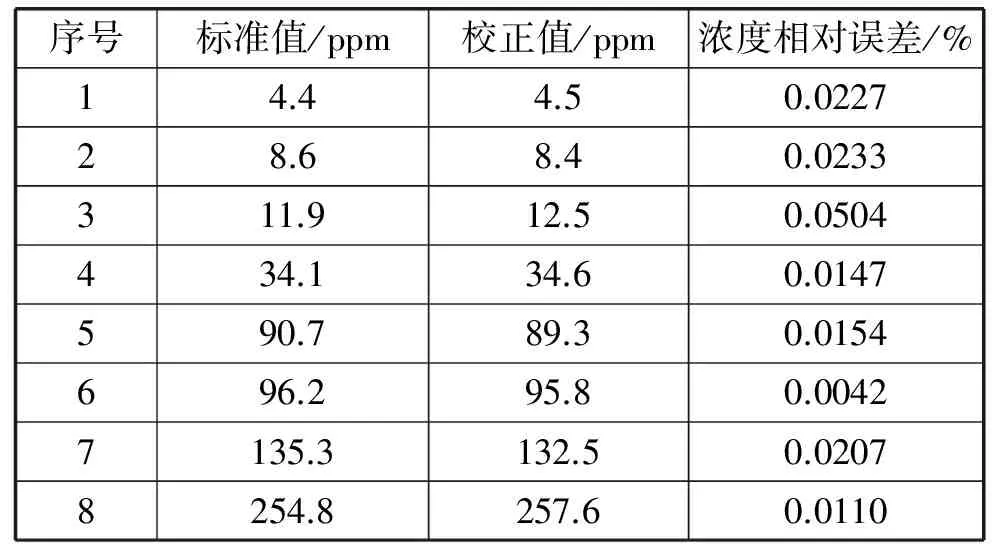
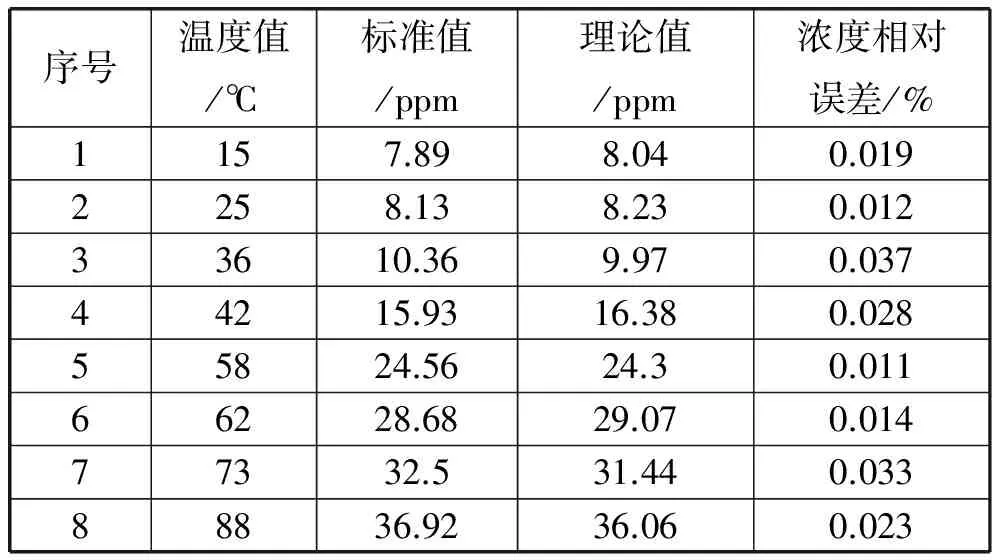
假设计量单位标准输出系统校准点S1与S2,响应幅值为V,气体浓度为C,其中校准点分别含有i,j个幅值修正点{V11,V12,…,V1i}和{V21,V22,…,V2j},且响应幅值介于两者之间,即V1p 令F1、F2为浓度C在S1、S2两点处的修正因子,用浓度值C分别对点S1p、S1q、S2m、S2n进行插值,并计算修正因子得: (5) (6) 用传感器响应值对两校准点插值计算得: (7) 则传感器响应真值VRL为: VRL=V·F (8) 1.3 基于改进PSO-BP神经网络的气敏特性建模 按误差反向传播学习算法训练而成的前馈性神经网络称BP神经网络。神经网络模型拓扑结构一般由多层构成,传输函数可为线性函数(pueline),也可为非线性函数(logsig、tansig)。根据误差性能函数不断调整网络权值和阈值,使得网络模型总的误差向减小的方向变化,传输特性不断逼近非线性系统函数关系,直到达到要求性能指标,具体算法可参见有关文献[13]。 多层神经网络结构,如图2所示。 图2 多层BP神经网络模型 输出总误差性能函数评价网络模型: (9) 式中,MSE为均方误差值,yi为网络的预测输出量,ygoal代表期望输出量,输入样本数N,每一层的权值和阈值修正公式为: x(i+1)=x(i)-αg(i) (10) (11) 式中,g(i)为第i次迭代的神经网络输出误差对各权值和阈值的梯度向量,x(i)为连接权值和阈值之间的向量,E(i)为误差性能函数。梯度的反方向是梯度最速的下降方向,α常数为学习速率。 本研究以气体浓度作为神经网络输入,传感器电压值作为网络输出,建立浓度与气敏传感器响应之间的映射关系,学习率取0.6。隐含层数与节点数的选择与确定主要采用凑试法与经验法结合的方式,本文结合以下经验公式[14]计算: (12) (13) S=log2n (14) 本文运用粒子群算法优化神经网络的权值与阈值,以提高模型的精度。粒子群算法由Eberhart博士和Kennedy博士共同提出,运用仿生学理论,借鉴动物集群运动机理[15],通过反复迭代,来寻求全局最优的智能优化算法[16]。通过对经典粒子群算法约束因子进行改进,提高约束因子提高算法性能。 (15) (16) xitk + 1=xitk+ξvitk+1 (17) 式中w为初始速度的惯性权重系数,取0.7298[17],c1和c2分别为粒子个体学习因子和社会学习因子,ζk与ηk为第k次迭代的随机数,取值范围[0,1],piDk与pgDk分别为第i个粒子的第t维向量经第k次迭代的历史最优矢量空间位置和整个粒子群的全局最优矢量空间位置,ξ为粒子速度约束因子,通常取值为1,φ=c1+c2,k为正常数。本研究将权值与阈值作为改进粒子用算法进行优化,利用响应输出与期望值之间存在的误差,确定模型的适应度函数,达到最优值搜索的目的[18],以获取神经网络权值和阈值。设适应度函数为: (18) 式中,f(xi,c)是神经网络第i个节点期望值,yi为第i个节点预测值,c为未知待定参数c=[c1,c2,…,cn]。 基于双参校准数据,运用神经网络与粒子群智能算法,便可建立一定温度下的气敏传感器响应信号与气体浓度之间的函数映射关系,即输出特性数学模型。 气敏传感器气敏特性由浓度、温度、湿度、以及气体种类等多种因素综合决定,而上述气敏传感器建模过程,是以环境中某一特定温度或者湿度条件不变的情况对气体敏感特性进行的定量分析,并不完全符合现实规律,因此很难满足实际自动化系统应用的需求。本节基于局部多项式回归分析思想进行非线性三维建模[19],考虑温度条件对模型的影响,建立浓度、温度以及传感器响应三者之间数学模型。 则有: (20) (21) 为计算方便,可将公式变换求解,固定y值, 构造对于变量x的最小二乘多项式: (22) 式中,φk(x)多项式互为正交,可由递推公式构造: φ0(x)=1φ1(x)=x-α0⋮ φk+1(x)=(x-αk)φk(x)-βkφk-1(x)k=1,…,p-1 (23) (24) 由回归理论可得多项式中的各项系数: (25) 同理构造y最小二乘多项式以及求得系数: (26) (27) 运用上述计算式求得曲面方程为: (28) 为验证上述智能算法和局部多项式回归分析曲面拟合算法所建参数修正数学模型与温度补偿模型的有效性以及建模效果。本实验将传感器置于待测气体中,采集电压、温度,校准浓度等数据进行实验。 3.1 实验思路与测试 本研究采用MATLAB编程将原始数据运用参数校准算法进行校准处理,获得校准数学模型,并将结果与传统的传感器校准算法所得校准结果进行比对,再对修正数据运用智能算法以及局部多项式回归拟合建模,最后基于此数学函数模型在构建的硬件系统上实现浓度实时显示。 3.2 实验结果对比分析 实验在不同温度下进行,采集到原始数据如图3(a)、(c)所示,被测量为气体浓度x(单位:ppm),系统响应量为负载电压(单位:V)。在该测量电路中,当温度不变时,负载电压与标定浓度之间单调递减性。运用参数校准算法获得校准数据如图3(b)、(d)所示。 图3 原始数据及校准参数 为选取气敏传感器数学模型的神经网络结构,本文采用试凑法对不同的隐含层数和隐含节点数分别对实验数据进行训练,与此同时对各神经网络结构经粒子群算法优化前后的性能进行比较。由于神经网络随机得到训练的初始权值和阈值,因此每次训练获得预测性能会有所差异,为确定更好的网络结构以实现更加优越的预测性能,用多次实验的平均值来表示。图4(a)、(b)为神经网络优化前的气敏特性曲线,图4(c)、(d)为神经网络优化后的气敏特性曲线。 图4 神经网络优化前后气敏特性曲线对比 温度补偿模型建立过程需要首先对数据进行网格化处理,取5×39个点,然后基于已建立的二维气敏特性曲线,运用局部多项式回归法进行三维曲面拟合,其浓度C,温度t,响应值S,全部样本三维分布,如图5所示,拟合得到的三维温度补偿模型,如图6所示。运用上述思想以及算法,确定x、y的幂次p=3,q=5,获得模型的非线性映射关系,并将8组测量数据与气体敏感特性理论数据进行对比分析,如表1和表2所示。 图5 校准网格数据三维分布图 图6 基于局部多项式回归拟合曲面 序号标准值/ppm校正值/ppm浓度相对误差/%14.44.50.022728.68.40.0233311.912.50.0504434.134.60.0147590.789.30.0154696.295.80.00427135.3132.50.02078254.8257.60.0110 表2 三维温度补偿模型数据分析(响应为0.416) 3.3 讨 论 1) 由图可以直观观察到本文气敏传感器参数修正算法可增加数据的平滑度,更有利于进行数据拟合建模。另外对二维气敏特性建模过程,发现运用改进的神经网络算法拟合所得曲线有明显优越性,模型精度更高,泛化能力更强。 2) 本文运用局部多项式回归算法进行三维建模,研究发现其中p、q取值对建模效果影响甚大,p、q取值越大三维曲面预测值与标准值之间的残差越小,但是幂次选择过高反而会造成曲面突起,曲面平滑度降低, 即过拟合现象,使模型不能准确反映气敏传感器气敏特性。在满足精度前提下,应尽可能降低模型幂次,以提高模型抗噪声能力。 准确进行传感器特性建模,消除非目标参量对系统影响,是目前自动化领域的方向[4]。本文采用一种优化数据的校准算法,然后基于神经网络建立二维数学模型,模拟传感器响应值与气体浓度之间关系,在此基础上添加影响因素,采用局部多项式回归算法,构建三维数学模型。但由于影响气敏传感器中半导体材料发生气-固化学反应影响因素多种多样,导致不同气敏传感器响应会有一定的差别,其准确度还待于进一步提高。结果表明,基于上述算法建立的数学测量模型可较精确模拟气敏特性变化规律,实现气敏传感器对气体准确测量,在系统自动化测控领域具有一定的参考价值。 [1] 尤克, 倪景秀.气敏传感器及其应用[J].仪表技术与传感器, 2007(7): 78-80. [2] 王康. SnO2基气敏传感器的制备与研究[D].济南:山东大学, 2013. [3] 崔远慧, 唐祯安, 余隽, 等.气体传感器的动态高精度测试系统设计[J].仪器仪表学报, 2010, 31(10): 2180-2185. [4] 唐炜, 徐晓苏.基于温度补偿的传感器建模方法及其应用[J].计量技术, 2007(2): 64-68. [5] 张琦, 潘孟春, 陈棣湘, 等.基于线性化参数模型的三轴磁场传感器校准方法[J].传感技术学报, 2012, 25(2): 215-219. [6] Wang D, Huang J.Neural network-based adaptive dynamic surface control for a class of uncertain nonlinear systems in strict-feedback form[J].IEEE Transactions on Neural Networks, 2005, 16(1): 195-202. [7] 何伟铭, 宋小奇, 甘屹, 等.传感器校正的优化灰色神经网络模型优化方法研究[J].仪器仪表学报, 2014, 35(3): 504-512. [8] 罗超宇, 李小曼, 韩骏浩, 等.改进的混合高斯背景建模算法[J].计算机应用与软件, 2015, 32(10): 209-212,230. [9] 俞阿龙.基于遗传神经网络的加速度传感器动态建模方法[J]. 仪器仪表学报, 2006, 27(3): 315-318. [10] 王聪, 陈填锐, 刘腾飞.确定学习与基于数据的建模及控制[J].自动化学报, 2009, 35(6): 693-706. [11] Lee J, Park T, Lee J, et al.Sensitive and Stable Gas Ionization Sensor Based on 3-D Single-Walled Carbon Nanotube Networks Suspended on ZnO Nanorods[J].IEEE Sensors Journal, 2015, 15(1): 260-263. [12] Kumar R, Das R R, Mishra V N, et al.A Neuro-Fuzzy Classifier-Cum-Quantifier for Analysis of Alcohols and Alcoholic Beverages Using Responses of Thick-Film Tin Oxide Gas Sensor Array[J].IEEE Sensors Journal, 2010, 10(9): 1461-1468. [13] 乔俊飞, 韩红桂.RBF神经网络的结构动态优化设计[J].自动化学报, 2010, 36(6): 865-872. [14] 雷成华, 刘刚, 李钦豪.BP神经网络模型用于单芯电缆导体温度的动态计算[J].高电压技术, 2011, 37(1): 184-189. [15] 张洪云.基于考虑个体心理属性的Vicsek模型的动态网络收敛性研究[D].广州:华南理工大学, 2014. [16] Kennedy J, Eberhart R.Particle Swarm Optimization[C]//IEEE International Conference on Neural Networks, 1995: 1942-1948. [17] Eberhart R C, Shi Y.Comparing Inertia Weights and Constriction Factors in Particle Swarm Optimization[C]//IEEE Congress on Evolutionary Computation. Piscataway: IEEE Service Center, 2000: 84-88. [18] Li C, Yang S.A General Framework of Multipopulation Methods with Clustering in Undetectable Dynamic Environments[J].IEEE Transactions on Evolutionary Computation, 2012, 16(4): 556-577. [19] 王华, 韩祖杰, 王志敏.高速铁路桥梁三维参数化建模方法研究[J].计算机应用与软件, 2013, 30(9): 71-73,76. [20] 马正华, 王腾, 杨彦, 等.神经网络模型在太湖出入湖河流水质预测中的应用[J].计算机应用与软件, 2013, 30(11): 172-175. AN OPTIMIZATION ALGORITHM BASED ON LOCAL POLYNOMIAL REGRESSIONFOR GAS SENSOR MODEL Zhou Changlin Zhao Shouguo Wang Zhenyi Liu Tong Liang Zhenhe (PLAInformationEngineeringUniversity,Zhengzhou450001,Henan,China) Accurate modeling of gas sensing sensor plays an important role in the accurate measurement of gas. Thus, a parameter calibration algorithm is proposed to solve the problem of unstable automatic system caused by gas sensor difference. Then, the relationship between the PSO-BP sensor response and the gas concentration is fitted by the combination of intelligent algorithm, and the two-dimension gas sensing character model is constructed. At the same time, an optimization method of regression analysis for the three dimensional modeling is proposed in order to reduce the temperature effect on mathematical model. Experimental and application results show that the parameters calibration method and the modeling methods improve the accuracy of the original model parameters and system reliability, and provide a high reference value for the preparation and application of gas sensor. Gas sensor Intelligent algorithm Parameter calibration Temperature compensation 2015-11-24。国家自然科学基金项目(61271104);河南省基础与前沿技术研究计划项目(122300410122)。周长林,副教授,主研领域:电子与通信工程,光电检测以及电磁兼容应用。钊守国,硕士生。王振义,硕士生。刘统,硕士生。梁臻鹤,硕士生。 TP391 A 10.3969/j.issn.1000-386x.2017.01.044
2 基于局部多项式回归的气敏特性建模研究


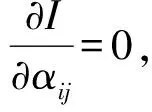
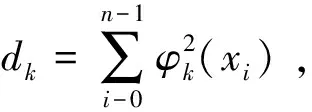
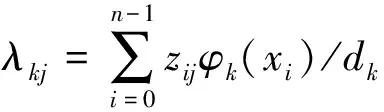
3 数学模型实例验证


4 结 语
