变异型鼓楼建筑结构及建造技艺研究

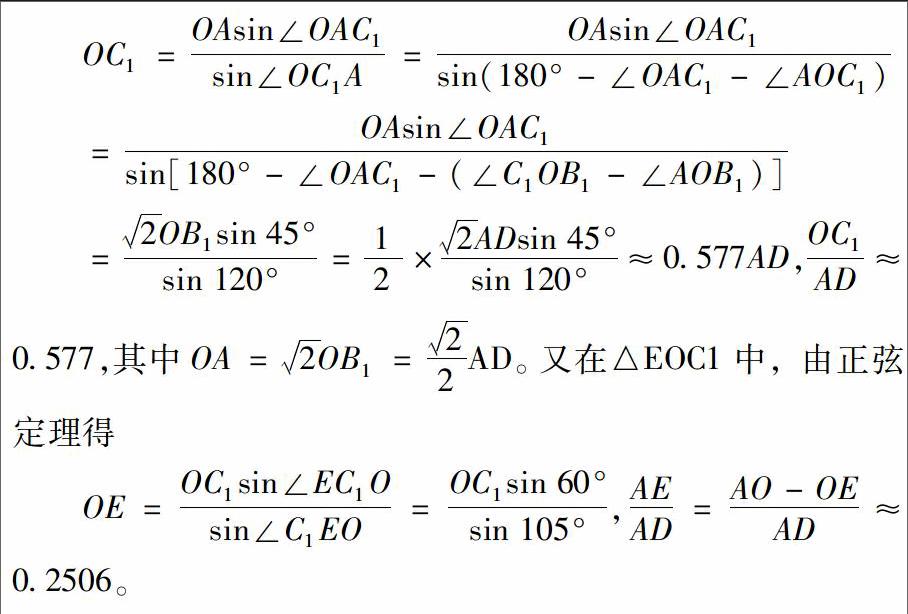
[摘要]通过对广西三江县侗族变异型鼓楼实地考察，分析它的几何结构以及变换的相关计算，发掘鼓楼的结构关系、同构原理、三角函数，以及等腰三角形三线合一等数学原理及思想方法。

[关键词]侗族鼓楼；鼓楼结构变换；墨线分割思想

[DOI]10.13939/j.cnki.zgsc.2017.02.191

鼓楼堪称是侗族建筑的明星，是侗族文化艺术的结晶，它代表本民族建筑艺术典范。依鼓楼屋檐的处理形式，可分为统一型和变异型两类。鼓楼的变异型其建筑技艺尤为独特，凸显出侗族人民对初等几何和数学原理的应用能力达到了较高的水平。本文主要以变异型为研究对象，以实地调查为基础，用数理方法研究和分析，来说明鼓楼建筑所用到的几何和数学原理。

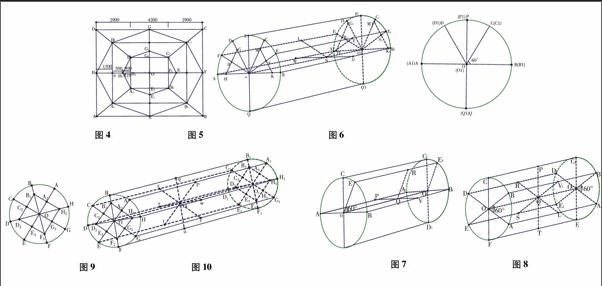
岩寨鼓楼外立面为九层重檐，下六层为方形重檐，上三层变为六角重檐，顶层为六角攒尖顶，宝塔为葫芦造型（见图1）。其在方形重檐变换为六角重檐的内部结构如图2所示，它在方形变换为六边形的过程充分体现了侗族人民已经较好地掌握了数学抽象思想和初等几何的应用。图3是鼓楼方形变换成六边形的一个平面图， A、B、C、D 四点分别是鼓楼的四根主承柱，A3、B1、C1、E、C2分别是鼓楼的五根瓜柱，线段AB、CD、A3C1、AE、B1C2、OB1分别是连接柱子的六根木枋，其中六边形为同心圆O的内接正六边形，在实际采访中得知鼓楼师傅在建造下方上六的变异型鼓楼时，其正六边形的边长=正方形的边长×C（C为常数），木枋AE=正方形的边长×C1（C1为常数），木枋A3C1=木枋A3O，即图3中的C1A3=AD×C，AE=AD×C1（仅以A3C1、AD、AE边为代表），A3C1=A3O。鼓楼师傅从长期的实践经验中发现C=0.575、C1=0.25较为适合，它是一个近似值，现以内四柱外十二柱的三江县岩寨鼓楼为代表，如果我们按照现代数学的方法来求，则有正六边形的圆心角∠A3OC1=60°、∠AOA1=45°，则∠OAC1=45°，在△AOC1中，由正弦定理知：

而侗族鼓楼师傅所用的测量工具是市尺（但对精度要求很高时会用到分，其中：1寸=10分），而侗族鼓楼师傅在测量或计算到钢尺分以后的数字通常采用控制误差小于半分的范围之内。侗族的计算多是与一半有关，因此鼓楼师傅近似地取0.575、0.25、0.75与其理论值相差很小，又在实际测量中也存在误差，故鼓楼师傅取C=0.575、C1=0.25、C2=0.75是有道理同时也符合实际的。

但侗族生活中的数学没有纯小数，遇到整数部分是0时通常放到下一个单位进行运算。这充分说明了侗族人民具有较好的近似计算能力，在鼓楼的尺寸和外形如何的变化，几乎所有鼓楼的造型、比例、尺度的处理得非常地完美。

研究发现，古代侗族没有量角器，建造一座平面结构图由正方形变换成正六边形的鼓楼，凿柱眼时需要做成30°和120°及60°的角，他们通常是作等腰三角形底边上的中线平分顶角去实现，过程如下。

首先，在准备好的呈圆柱体（实际上是不规则）的原木（如图5）两头横截面分别掉垂线PQ及P1Q1，并用墨线分别连接PP1及QQ1；后将原木旋转90°，重复前面的方法作出AB，A1B1，AA1，BB1，且有PQ⊥AB，垂足为O，P1Q1⊥A1B1，垂足为O1；这实际上是将原木抽象为直线O O1的过程。

其次，在原木两头的横截面上用事先做好的三角形模板（这是鼓楼建筑师的基本工具）的一边靠在OB（或O1B1）上，顶点与O（或O1）重合画出另一边OC（或O1C1）（见图6）。然后，分别在OB、OC（或OB1，OC1，）上取K、M（或K1，M1），使OK=OM（或OK1=OM1），连接KM（或K1M1），并找出KM（或K1M1）的中点S（或S1），连接OS（或OS1）其延长线与横截面的边缘交于E（或E1），用墨线连接EE1、用同样的方法作出墨线FF1、在EE1、FF1、BB1及AA1上的任一指定位置T、L、U及W上沿直线OO1垂直相交的方向上钻孔（凿柱眼），孔与孔（柱眼）TN与LN所确定的方向成120°角，TN与NU所确定的方向成30°角。六边形的另四根柱子（凿柱眼）（见图7）的方法与上面（见图5）类似，所不同的是在EE1、AA1及BB1上的任一指定位置R、P及V上沿直线OO1垂直相交的方向上钻孔（凿柱眼），RQ与PQ所确定的方向成120°角，RQ与VQ所确定的方向成60°度角。最后，用六根等长的木枋与柱子连接即可得到正六边形。雷公柱用于支撑鼓楼顶部的中间独柱。制作一个平面结构为正六边形鼓楼的雷公柱，凿柱眼是需要图7所示（或120°）的角，做法和见图5类似，所不同的是BO（或BO1）和CO（或CO1）的延长线分别与截面的边缘交于E（或E1）、F（或F1），用墨线连接EE1、FF1（见图8）。然后，在EE1、FF1及AA1上的任意指定位置S，V及U上沿直线OO1垂直于交线的方向钻孔（凿柱眼），使SQ、TQ及UQ分别与BB1、CC1及图8DD1相交于V、P和R，孔与孔（柱眼）SV，TP及UR所确定的方向成60°（或120°）。

而制作一个平面结构为正八边形的雷公柱时，凿柱眼是需要45°（或135°）的角，他们通常是通过作等腰直角三角形底边上的中线平分直角去实现的。图9是雷公柱的一个横截面，DH∩BF=O，且DH⊥BF，取OB2=OD2=OF2=OH2，依次连接B2D2、D2F2、F2H2、H2B2，并取B2D2、D2F2、F2H2、H2B2的中點分别为C2、E2、G2、A2，然后分别连接OC2、OE2、OG2、OA2，其延长线与截面的边缘分别交于C、E、G、A，在柱子的指定位置p、q、r及s上沿直线OO1垂直于交线的方向钻孔（凿柱眼），分别与AE、BF、CG、DH交于t、u、v及w，孔与孔（柱眼）pt、qu、rv及sw所确定的方向成45°（或135°）角（图10）。

仅此，我们看到了变异型鼓楼的建造、变换过程中涉及数学中集合的同构的思想方法， 鼓楼是记载着侗族千百年历史政治和文化的一本木建实物书，更是一部经典的数学书实物书，而这部经典的数学书是由没有文字的侗族人民像传承侗族大歌那样口传心授顽强地传承下来的。

参考文献：

[1]高雷，邹妮妮，戴舜松，等.白描·鼓楼风雨桥测绘研究实录[M].南宁：广西美术出版社，2011.

[2]罗永超.鼓楼人类文明“童年时期”数学文化结晶[J].数学通报，2007，46（11）：9-11.

[3]吴秀吉.侗族生活中的数学[J].数学通报，2011，50（10）.