面向EMD分解的径流分量重构方法对比研究

张洪波+余荧皓+孙文博+曹巍

摘要：水文序列非平穩与非线性的复杂变化导致水文序列中长期预测的准确性备受质疑。“分解-预测-重构”模式作为一种新的有效的预测思路近年来备受业界和学者关注。但受到高频分量预测误差大、趋势走向不确定等问题困扰，这种模式在发展过程中仍有诸多需要改进的地方。其中，径流分量的重构方法是控制高频分量误差，提高整体预测精度的关键性措施，其优劣对预测效果实现有着重要的意义。基于经验模态分解（EMD）和自回归模型（AR）建立“分解-预测”耦合模型，结合粒子群优化（PSO）算法，提出PSO重构系数优化法和高频分量剔除+重构系数优化法两种重构方法，结合前人提出的高频分量剔除法，以陕北丁家沟站、关中华县站、陕南白河站为算例，对不同重构方法的效果进行对比研究。研究结果表明：基于高频分量剔除法、PSO重构系数优化法、高频分量剔除+重构系数优化法三种重构方法的预测效果均较好，五项误差评价指标均优于标准重构法，三种重构方法均可不同程度地提高预测精度。对比研究发现：高频分量剔除法在重构过程中剔除了最不稳定且最难预测的高频分量，提高了预测精度，但提升效果有限；PSO重构系数优化法对所有径流分量赋予优化重构系数并重构，可最大程度地实现分量间的平差，有效提高了预测精度；高频分量剔除+重构系数优化法综合上述两种方法的优势，取得了比其他方法更好的预测效果。

关键词：水文学及水资源；径流预测；EMD分解；重构；重构系数优化

中图分类号：P338.2文献标志码：A文章编号：1672-1683（2017）01-0060-07

Abstract：The accuracy of mid-and long-term forecast on hydrological time series is highly questioned due to the non-stationary and nonlinear complex changes of the series.The "Decomposition-Prediction-Reconstruction" model，as a new and effective forecasting method，has captured the attention of many scholars in related fields in recent years.But troubled by large errors in high-frequency component prediction，uncertain trend and other issues，this model still requires a lot of improvements in the development process.Among all the improvements，reconstruction of runoff component is intensely crucial in controlling high-frequency component prediction error and improving prediction accuracy of the hydrological series.To do this，the "Decomposition - Prediction" hybrid model was established in this paper using empirical mode decomposition （EMD） and autoregressive model （AR）.Two reconstruction methods were proposed based on the particle swarm optimization （PSO） algorithm，which were the PSO-based reconstruction coefficient optimization method and the high-frequency component removal & reconstruction coefficient optimization method.These two methods plus the previous high-frequency component removal method were used to compare the efficacy of hydrological forecasting in a case study on Dingjiagou station in northern Shaanxi，Huaxian station in middle Shaanxi and Baihe station in southern Shaanxi.The results showed that the high-frequency component removal method，PSO-based reconstruction coefficient optimization method and high-frequency component removal & reconstruction coefficient optimization method all predict better than the standard reconstruction method，as reflected by five error evaluation indicators.Thus it can be drawn that these three reconstruction methods can improve the prediction accuracy in different degrees.High-frequency component removal method emphasizes removing the high-frequency component，which is the most unstable and unpredictable，so as to enhance the prediction accuracy，but only by a limited margin due to the simple removal process.PSO-based reconstruction coefficient optimization method is to optimize the reconstruction coefficients of all runoff components and to reconstruct the forecasted series.It can reduce errors during components reconstruction to the greatest extent and improve the prediction accuracy effectively.High-frequency component removal & reconstruction coefficient optimization method combines the above two methods and predicts better than all the other methods.

Key words：hydrology and water resources；runoff prediction；empirical mode decomposition；reconstruction；reconstruction coefficient optimization

在全球氣候变化和人类活动的双重影响下，河川径流序列已经从一个相对平稳过程转变为一个复杂的非平稳、非线性过程，这种变化使得很多基于平稳性假设的水文预测预报方法在变化环境下的应用受到了极大的挑战。由于径流受到降雨、蒸发、大气循环等诸多因素的影响，故径流序列中包含了许多不同频率的分量[1]。很多学者尝试通过分解-预测-重构的方式寻找水文序列中的稳定周期变化量和趋势变化量，对其进行适宜性预测，以改善由于水文序列非平稳和非线性变化引发的水文中长期预报失真的现状[2-7]。“分解-预测-重构”模式的特点在于将一个“杂乱无章”的水文序列，经过分解得到多个相对稳定的周期变化序列（IMFs）和一个趋势性残余序列（Residual）。由于现有预测方法对稳定变化的序列一般具有较好的预测精度，因此重构后其可获得较原序列更好的预测效果[8]。如张敬平等利用经验模态分解（EMD）与径向基（RBF）神经网络相结合的方法预测径流量，发现该方法相对于直接预测具有更高的精确度[9]；赵雪花等将EMD分解技术与RBF、自回归滑动平均模型（ARMA）、灰色模型GM（1，1）相结合，分析对比了不同数据驱动模型在河川径流预测中的预测效果[10]。曹丽青等将EMD分解与多尺度统计动力学模型相结合，构建了研究区域的动力学预报方程，并对不同重构分量情形下的预测精度进行了对比[11]。钱晓燕等提出EMD与最小二乘支持向量机（LS-SVM）模型相耦合的径流中长期预测方法，采用EMD进行序列分解，LS-SVM模型用于预测IMFs分量，取得很好的预测效果[12]。

研究中发现，由于高频分量预测误差较大，重构时高频预测误差会直接影响序列的整体预测效果[13]。于是有学者开始尝试对“分解-预测-重构”预测模式中的重构环节做出改进。黄生志等提出了基于经验模态分解的支持向量机（EMD-SVM）预测模型，在重构过程中剔除了高频分量（IMF1），提高了预测精度[1]；林树宽等将基于经验模态分解和支持向量回归模型的耦合模型运用于非线性、非平稳时间序列预测中，重构环节采用支持向量回归法对分量进行非线性组合，获得了较高的预测精度[14]。

经过对已有成果的分析，笔者发现不同的重构方法对于预测精度提升的效果并不相同，故本文基于经验模态分解（EMD）和自回归模型（AR）建立了“分解-预测”的耦合模型，并以此为基础，对高频分量剔除法以及本文提出的PSO重构系数优化法、高频分量剔除+重构系数优化法三种重构方法的提升效果进行对比分析，以揭示不同重构方法对序列预测精度的影响。

1 研究方法

1.1 经验模态分解（EMD）

经验模态分解（Empirical Mode Decomposition，EMD）是由黄锷（N.E.Huang）等人于1998年创造性地提出的一种新型自适应信号的时频处理方法[15]。该方法主要针对非平稳及非线性数据，依据数据自身的时间尺度特征来进行信号分解，得到多个具有物理意义的平稳的固有模态函数（Intrinsic Mode Function，IMF）和具有单一性的趋势项（Residual）。在水文应用中，EMD分解得到的各径流分量规律性更强，能够大大提高预测精度[16-17]。经验模态分解的具体步骤如下。

步骤1：找出原始时间序列X（t）的所有极大值点与极小值点，用三次样条插值函数拟合时间序列的上、下包络线，上、下包络线的均值m（t）为

步骤3：检验h（t）是否可作为固有模态函数（IMF），需满足以下两个条件：（1）在任意时刻，有极大值定义的上包络线和下包络线均值为零；（2）对于一个分量信号，极值点与过零点数目一样或者只差一个[18]。若不满足这两个条件，则把h（t）当作原始序列重复步骤1、2，直到满足以上两个条件，求出第一个固有模态函数I1（t）为止。

步骤4：用原始序列X（t）减去第一个固有模态函数I1（t）得到剩余序列r1（t）：

步骤5：将r1（t）作为新的原始序列重复步骤1至4，分解出所有的固有模态函数I1（t）、I2（t）、…、In（t），直至In（t）为一单调的残余趋势项（Residual）为止。

1.2 基于EMD的分解-预测-重构模式

通过对径流序列进行EMD分解，得到多个固有模态函数（IMFs）和一个残余趋势项（Residual），即将非平稳径流时间序列分解为多个趋于平稳的径流分量和一个趋势径流分量。然后对这些径流分量分别应用自回归模型（AR）进行预测。AR模型是时序方法中最基本、应用最广的时序模型，它对平稳时间序列预测一般能取得较高的预测精度[19]。可表示为：

对于一个径流分量时间序列xt，有

式中：at为满足均值为零、方差为σ2a的独立正态分布；φ1，φ2，…，φn称为模型参数；n为模型的阶数。用当前变量的时间序列作为因变量序列，并利用当前变量向过去推移若干期数的时间序列作自变量序列，分析因变量序列和一个或多个自变量序列之间的相关关系，建立回归方程进行预测，可实现径流序列的有效外延，即预测。

以分量预测结果为基础，将径流分量的预测值乘以对应的重构系数进行重构，即可得到预测精度较传统的标准重构法更好的新的预测序列。

1.3 重构方法

传统的标准重构法是将预测得到的各径流分量直接对应相加，得到预测序列。其缺点在于径流分量的预测误差将被直接叠加到预测序列上，进而导致预测效果不理想。为了解决这一问题，提高预测精度，不同的重构方法被应用于径流分解后的重构过程中，但结果不甚相同。为了分析不同重构方法对预测结果的影响，本文提出了PSO重构系数优化法、和高频分量剔除+重构系数优化法两种重构方法，并与标准重构法、高频分量剔除法进行对比研究，分析其优劣。图1显示了不同重构方法的基本原理。

1.3.1 高频分量剔除法

高频分量（如IMF1）是径流分量中最不平稳、非线性最强的一个径流分量。由于其波动范围大，且难以预测，是重构后预测误差的主要来源。相关研究表明，愈不平稳、非线性愈强的原始序列经过EMD分解后将产生愈不规则、愈难预测的高频分量，预测精度也将大打折扣。故有些学者在重构时采取高频分量剔除法[1]，即剔除高频分量（如IMF1），而将其余径流分量进行重构（如图1a），以期提升预测精度。

1.3.2 PSO重构系数优化法

粒子群优化算法（Particle Swarm Optimization，PSO）于1995年由Kennedy和Eberhart共同开发[20]。基本思想是通过群体中个体之间的协作和信息共享，从随机解出发，通过迭代寻找出最优解。其算法在可行解空间中初始化一群粒子，每个粒子都代表优化问题的一个潜在最优解，用位置、速度和适应度值表征每个粒子，其中适应度值的好坏表示粒子的优劣。粒子通过跟踪个体极值（Pbest）和群体极值（Zbest）在解空间中运动，动态调整飞行速度，以期向群体中最好微粒位置飞行，从而使所优化问题得到最优解[21]。

结合PSO的寻优原理，将各个径流分量的重构系数值与PSO的粒子相对应，径流分量个数与PSO的空间维数相对应，时间序列率定期的相对误差绝对值的平均值（MAPE）与PSO的适应度值相对应。PSO重构系数优化主要以率定期的模拟值为基准，当重构之后得到的新序列的预测误差最小时，PSO优化终止，各径流分量按照重构系数进行重构（图1b）。这里需要是说明的是，由于率定期的模拟值与原始序列分解值之间存在误差，因此优化得到的重构系数之和不一定为1。而PSO优化的效果实现主要是依据各个径流分量间预测误差相互抵消，即平差。在预测分量的重构过程中，该方法可一定程度上减小重构误差的叠加，从而实现预测精度的显著提升。

1.3.3 高频分量剔除+重构系数优化法

基于高频分量剔除法，提出高频分量剔除+重构系数优化法。其在重构过程中先去除高频分量（如IMF1），对其余径流分量进行PSO优化，求出系数后再进行重构（图1c）。此方法在重构过程中去除了误差的主要来源，即高频分量（如IMF1），同时将剩余的径流分量按照系数重构，兼具两种方法的特点，以期最大程度上减小了预测序列的误差，提高了預测精度。

2 实例计算

2.1 算例与评价指标选取

陕西省位于中国西北部，纵跨黄河、长江两大流域。全省总面积20.6万km2，地形特点为南北长、东西窄，地势南北高，中部低。由北向南依次为陕北黄土高原、关中平原、陕南秦巴山地。受气候条件、地形、地貌、水文地质条件等的差异性影响，陕北、关中、陕南三个地区的水资源分布、产水量、径流特征等显著不同。为了验证研究成果的普适性，本文分别选取无定河流域的丁家沟站、渭河流域的华县站、汉江流域的白河站为研究对象。三站分别位于陕西省的陕北黄土高原、关中平原、陕南秦巴山地三个差异性地区，其水文特征各具代表性，也更适于反映研究方法在不同区域的适用性。

本次研究数据采用的是丁家沟站（1959年-2010年）、华县站（1959年-2009年）、白河站（1935年-1995年）的实测年径流序列，数据序列来源于黄委会水文局汇编的《黄河流域水文资料》和陕西省水利厅。所选站点均属于研究区内控制流域面积大，且可代表该流域水文特性的站点。

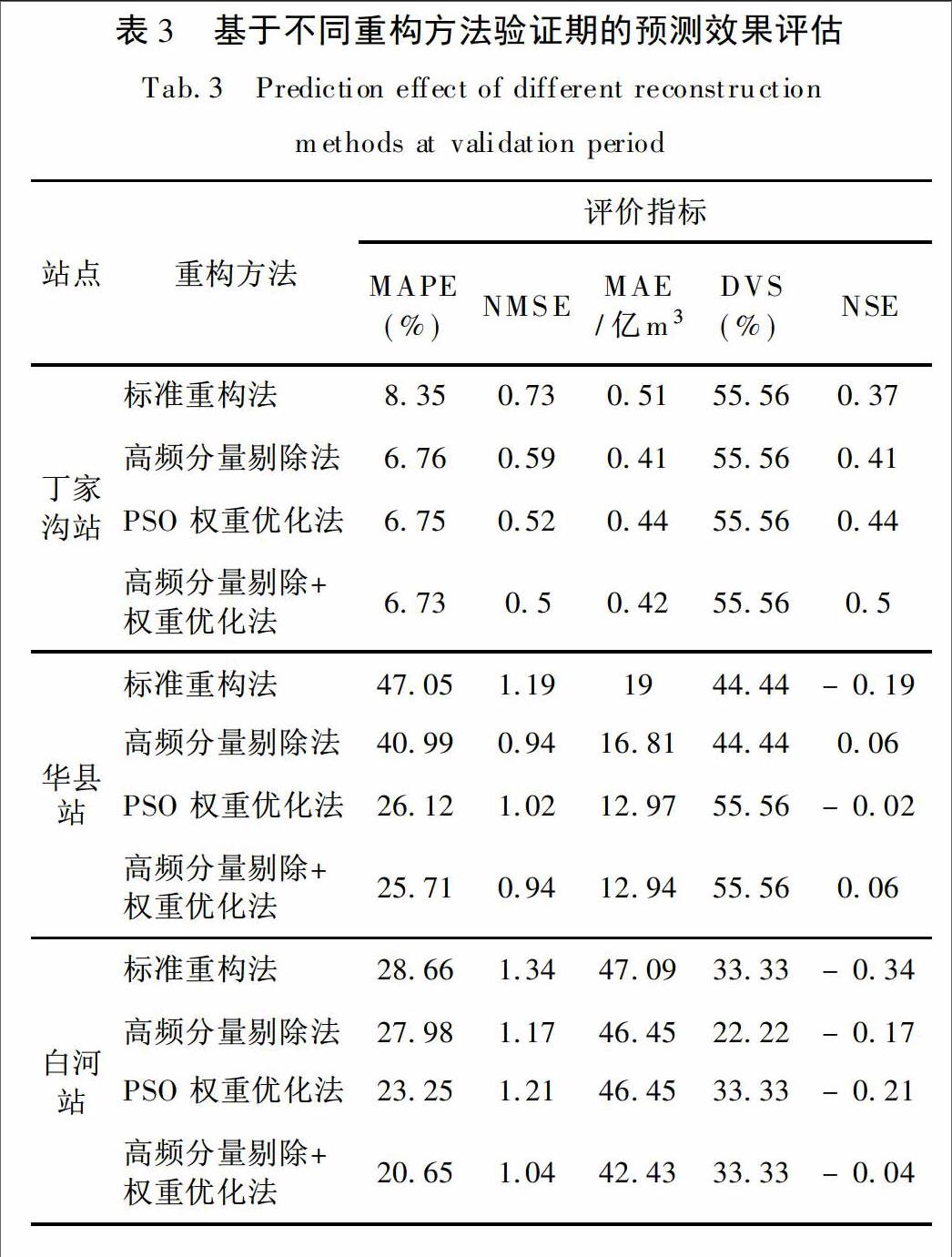
为了检验径流预测效果的好坏，本文选取相对平均误差的绝对值（MAPE）、标准均方误差（NMSE）、平均绝对误差（MAE）、方向变差对称值（DVS）和纳什效率系数（NSE）5种误差评价指标[22]来对预测效果进行综合性衡量与评价。其中，MAPE、NMSE和MAE的数值越小、DVS的数值越大、NSE越接近1，说明拟合越精确，预测效果越好。

2.2 EMD分解与预测结果

2.2.1 EMD分解

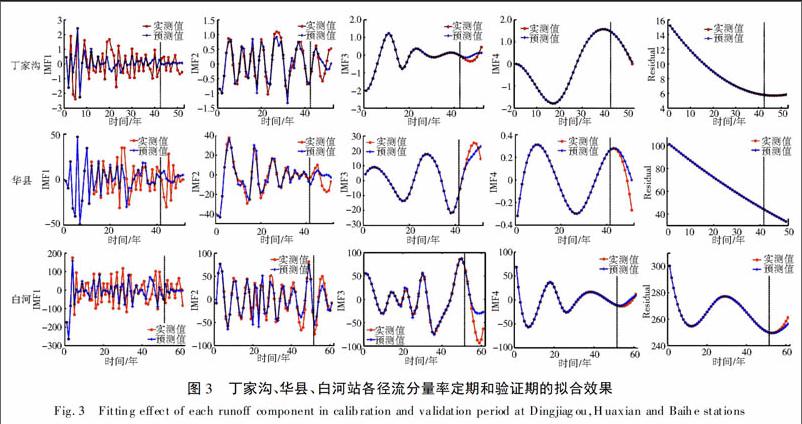
对丁家沟站、华县站和白河站的实测年径流序列进行EMD分解，结果见图2。由图2可知，三个水文站的实测径流序列均可分解为4个固有模态函数（IMFs）和1个残余趋势项（Residual）；随着分解次数的增加，IMF1-IMF4均逐渐呈现规整和平稳化，丁家沟站和华县站的残余趋势项呈缓慢递减趋势，白河站的残余趋势项略有波动，呈缓慢上升趋势。

2.2.2 基于AR模型的径流预测

选取丁家沟站1959年-2000年（42年）为率定期，2001年-2010年（10年）为验证期；华县站1959年-1999年（41年）为率定期，2000年-2009年（10年）为验证期；白河站1935年-1985年（51年）为率定期，1986年-1995年（10年）为验证期。在各个站点上，利用AR模型，分别对EMD分解得到的径流分量子序列进行预测，得到各径流分量率定期和验证期的预测效果评估见表1。

预测序列拟合效果见图3，图中虚线之前为率定期，虚线之后为验证期。由表1和图3可知，低频分量（如IMF3、IMF4、Residual）在率定期的拟合效果好，实测曲线和预测曲线接近重合，验证期的预测效果虽在极值点上存在偏差，但整体预测效果较好。

而高频分量（如IMF1、IMF2）在率定期的拟合效果并不理想，验证期的预测效果也不佳。如若直接重构，整个径流序列的预测误差也将主要源自高频分量，因此降低高频分量预测误差对整体预测结果的影响是提高整体预测精度的根本。为了消减高频分量的误差影响，同时也避免过多的信息丢失，本文在高频分量剔除法和高频分量剔除+重构系数优化法中主要剔除了IMF1，而保留了IMF2。2.3 重构系数

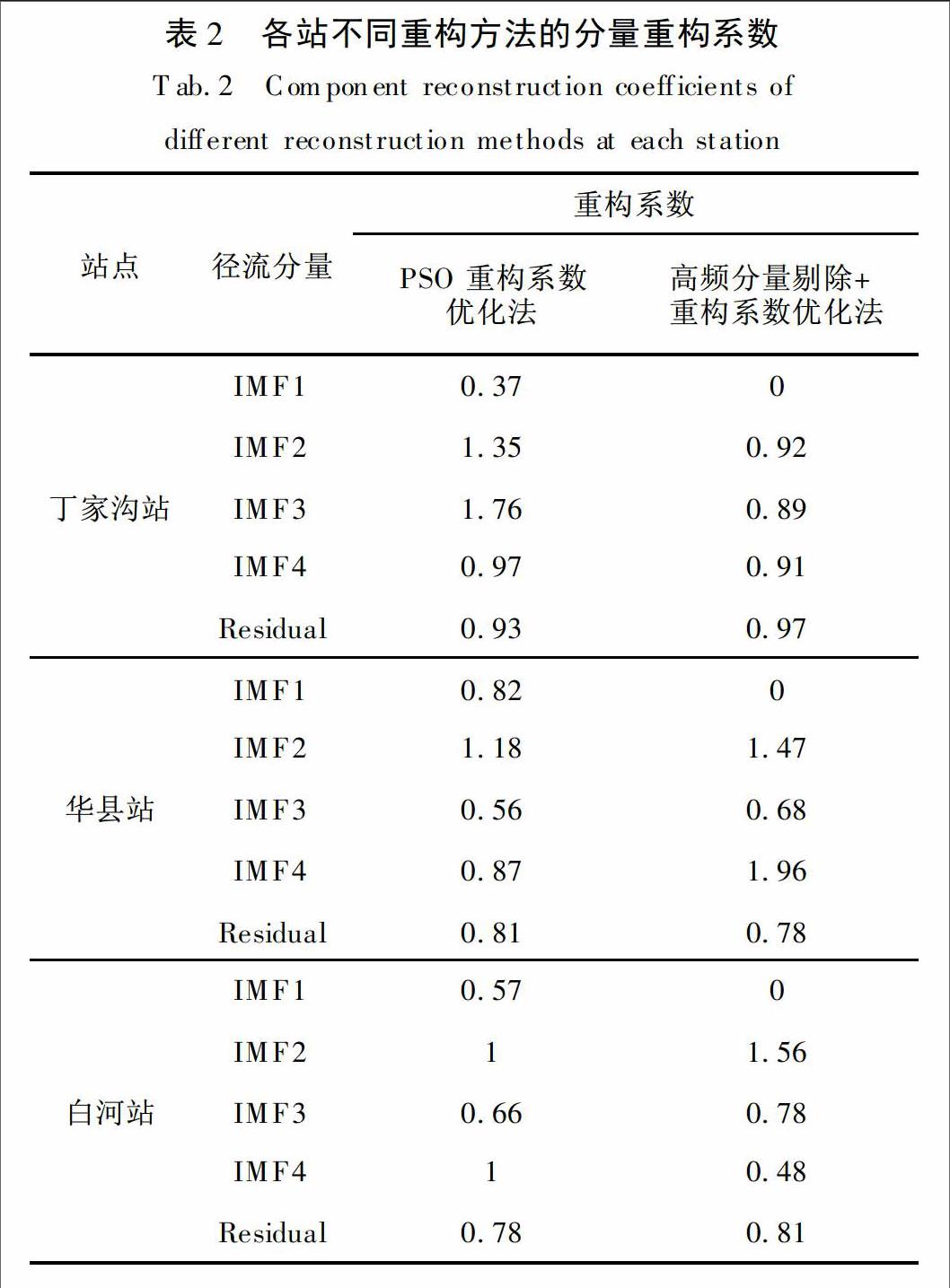
采用PSO重构系数优化法和高频分量剔除+重构系数优化法，基于率定期的模拟数据对丁家沟站、华县站、白河站三站的各径流分量求取重构系数，并按此重构系数重构验证期的预测分量，得到最终径流序列的预测结果。PSO重构系数优化法和高频分量剔除+重构系数优化法的重构系数见表2。

2.4 重构效果分析

结合标准重构法，对四种重构方法的提升效果进行对比分析，预测序列在验证期的预测效果评估如表3所示。结果显示，标准重构法的预测误差较大，预测效果不甚理想，其中华县站平均相对误差绝对值（MAPE）更是达到了47.05%。在陕北黄土高原、关中平原、陕南秦巴山地三个差异性地区，高频分量剔除法、PSO重构系数优化法、高频分量剔除+重构系数优化法三种重构方法预测结果的误差评价指标值均优于标准重构法，说明三种重构方法均能不同程度上减小误差，提高预测精度，且这一结论对不同流域均适用。

通过对比，不难发现高频分量剔除法剔除了最不稳定、且预测精度最差的高频分量（IMF1），控制了误差来源，预测效果得到了有效提升。但由于受PSO重构系数优化法虽然叠加了高频分量（IMF1），但在寻优过程中，最大程度上相互抵消了各径流分量的预测误差，故可获得相对比较满意的预测效果。丁家沟站、华县站和白河站三站预测效果的平均相对误差绝对值（MAPE）分别为6.75%、26.12%和23.25%，均满足中长期水文预测精度要求，可见此重构方法有效、可行。但是由于PSO算法的终止条件是使得率定期的MAPE值最小，故在验证期高频分量IMF1的预测误差仍会影响整体预测效果。

高频分量剔除+重构系数优化法综合了上述两种方法的优势，不但剔除了预测效果最差的高频分量（IMF1），同时对其余径流分量进行了重构系数优化，一定程度上可相互抵消其预测误差。从丁家沟站、华县站和白河站三站的评价指标看，较其他重构方法均有明显改善，其中平均相对误差绝对值（MAPE）达到了6.73%、25.71%和20.65%，系所有重构方法中预测精度最高的。同时，三个不同地域的站点的预测结果也表明高频分量剔除+重构系数优化法的优越性并非偶然，而是具有一定的普适性。

3 结论

基于分解-预测-重构的预测模式，对比了不同径流分量重构方法对径流预测效果的影响，并得出以下结论。（1）相比标准重构法，高频分量剔除法、PSO重构系数优化法、高频分量剔除+重构系数优化法三种重构方法在不同流域均可在不同程度上减小预测误差，提高预测精度，具有普适性；（2）高频分量剔除法在重构过程中剔除了最不稳定且最难预测的高频分量，可提高预测精度，但预测精度提升效果有限；（3）PSO重构系数优化法求取每个径流分量的重构系数并按照重构系数进行重构，重构过程中可最大程度上在各径流分量间进行预测误差的平差，可有效提高预测精度；（4）高頻分量剔除+重构系数优化法综合上述方法的优势，剔除了预测误差最大的高频分量，并对其余径流分量按照重构系数进行重构，重构后预测效果最好。（5）基于PSO重构系数优化法与高频分量剔除+重构系数优化法的预测模式效果较好，满足中长期水文预测精度要求，可作为未来基于分解-预测-重构的预测模式的重构方法。

参考文献（References）：

[1] Huang S Z，Chang J X，Huang Q，Chen Y T.Monthly streamflow prediction using modified EMD-based support vector machine.[J].Journal of Hydrology，2014，511（7）：764-775.DOI：10.1016/j.jhydrol.2014.01.062

[2] 李亚娇，沈冰，李家科.年径流预测的小波系数加权和模型[J].应用科学学报，2007，25（1）：96-99.（LI Ya-jiao，SHEN Bing，LI Jia-ke.Weighted summation of wavelet coefficients model for annual runoff prediction[J].Journal of Applied Sciences，2007，25（1）：96-99.（in Chinese））

[3] 徐廷兵，马光文，黄炜斌，等.基于小波分析的BP网络预测模型及其在年径流预测中的应用[J].水电能源科学，2012，30（2）：17-19.（XU Ting-bing，MA Guang-wen，HUANG Wei-bin，et al.BP network prediction model and its application in annual runoff forecasting based on wavelet analysis[J].Water Resources and Power，2012，30（2）：17-19.（in Chinese））

[4] 蒋晓辉，刘昌明.基于小波分析的径向基神经网络年径流预测[J].应用科学学报，2004，22（3）：411-414.（JIANG Xiao-hui，LIU Chang-ming.Radial basis function networks based on wavelet analysis for the annual flow forecast[J].Journal of Applied Sciences，2004，22（3）：411-414.（in Chinese））

[5] 周惠成，彭勇.基于小波分解的月径流预测校正模型研究[J].系统仿真学报，2007，19（5）：1104-1108.（ZHOU Hui-cheng，PENG Yong.Research of monthly discharge predictor-corrector model based on wavelet decomposition[J].Journal of System Simulation，2007，19（5）：1104-1108.（in Chinese））

[6] 闫强，李瑞丽，武鹏林.基于小波分析技术的中长期径流预测模型研究[J].人民黄河，2013，35（7）：26-27，30.（YAN Qiang，LI Rui-li，WU Peng-lin.Study on the medium and long term runoff forecast model based on wavelet analysis[J].Yellow River，2013，35（7）：26-27，30.（in Chinese））

[7] 马细霞，穆浩泽.基于小波分析的支持向量机径流预测模型及应用[J].灌溉排水学报，2008，27（3）：79-81.（MA Xi-xia，MU Haoze.Runoff prediction model and its application based on wavelet analysis and support vector machine[J].Journal of Irrigation and Drainage，2008，27（3）：79-81.（in Chinese））

[8] 王永文，付娟，金菊良，等.基于经验模态分解的年径流组合预测模型[J].水电能源科学，2010，28（10）：16-18.（WANG Yong-wen，FU Juan，JIN Ju-liang，et al.Combination prediction model of annual runoff based on empirical mode decomposition[J].Water Resources and Power，2010，28（10）：16-18.（in Chinese））

[9] 张敬平，黄强，赵雪花.经验模态分解和RBF网络在径流预测中的应用[J].干旱区资源与环境，2014，28（6）：118-123.（ZHANG Jing-ping，HUANG Qiang，ZHAO xue-hua.Application of empirical mode decomposition and RBF neural network to runoff forecasting[J].Journal of Arid Land Resources and Environment，2014，28（6）：118-123.（in Chinese））

[10] 趙雪花，陈旭，袁旭琦.基于EMD的数据驱动模型在径流预测中的应用[J].系统工程，2014，32（9）：150-154.（ZHAO Xue-hua，CHEN Xu，YUAN Xu-qi.Application of data-driven model based on empirical mode decomposition for runoff forecasting[J].Systems Engineering，2014，32（9）：150-154.（in Chinese））

[11] 曹丽青，林振山.基于EMD的HHT变换技术在长江三峡水库年平均流量预报中的应用[J].水文，2008，28（6）：21-24.（CAO Li-qing，LIN Zhen-shan.Application of EMD-based hilbert-Huang transform technology in forecasting mean annual discharge of the Three Gorges Reservoir on the Yangtze River[J].Journal of China Hydrology，2008，28（6）：21-24.（in Chinese））

[12] 钱晓燕，邵骏，袁鹏，等.基于EMD和LS-SVM的中长期径流预报[J].水电能源科学，2010，28（4）：11-13.（QIAN Xiao-yan，SHAO Jun，YUAN Peng，et al.Mid-long term runoff forecasting base on EMD and LS-SVM[J].Water Resources and Power，2010，28（4）：11-13.（in Chinese））

[13] 高祥涛，李士进.基于经验模态分解的水文时间序列预测研究[J].水文，2009，29（3）：66-68.（GAO Xiang-tao，LI Shi-jin.Study of hydrological time series prediction based on empirical mode decomposition[J].Journal of China Hydrology，2009，29（3）：66-68.（in Chinese））

[14] 林树宽，杨玫，乔建忠，等.一种非线性非平稳时间序列预测建模方法[J].东北大学学报：自然科学版，2007，28（3）：325-328.（LIN Shu-kuan，YANG Mei，QIAO Jian-zhong，et al.Prediction modelling method for non-linear and non-stationary time series[J].Journal of Northeastern University （Natural Science），2007，28（3）：325-328.（in Chinese））

[15] Huang N E，Shen Z，Long SR，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London A，1998，454：903-995.（DOI：10.1098/rspa.1998.0193）

[16] 陈旭，赵雪花.基于EMD分解的AR模型在年径流预测中的应用[J].水电能源科学，2014，32（7）：14-18.（CHEN Xu，ZHAO Xue-hua.Application of auto regressive model to annual runoff forecasting based on empirical mode decomposition[J].Water Resources and Power，2014，32（7）：14-18.（in Chinese））

[17] 袁潇晨，金菊良，王宗志，等.基于经验模态分解的年径流自忆性预测模型[J].水电能源科学，2010，28（6）：1-3，169.（YUAN Xiao-chen，JIN Ju-liang，WANG Zong-zhi，et al.Self-memory model based on empirical mode decomposition for annual runoff prediction[J].Water Resources and Power，2010，28（6）：1-3，169（in Chinese））

[18] Huang N E，Shen Z，Long S R，et al.A new view of nonlinear water waves：the Hilbert spectrum[J].Annual Reviews of Fluid Mechanics，1999，31 （1）：417-457.DOI：10.1146/annurev.fluid.31.1.417

[19] 刘洪斌，武伟，魏朝富，等.AR模型在土壤水分动态模拟中的应用[J].山地学报，2004，21（1）：121-125.（LIU Hong-bin，WU Wei，WEI Chao-fu，et al.Soil water dynamics simulation by autoregression models[J].Journal of Mountain Science，2004，21（1）：121-125.（in Chinese））

[20] Tang J，Zhao X J.An Enhanced Opposition-based Particle Swarm Optimization[C].Intelligent Systems，2009 WRI Global Congress （GCIS 2009）[A]，Xiamen，China，2009：149-153.DOI：10.1146/10.1109/GCIS.2009.56

[21] 唐俊.PSO算法原理及應用[J].计算机技术与发展，2010，20（2）：213-216.（TANG Jun.Principle and Application of PSO Algorithm[J].Computer Technology and Development，2010，20（2）：213-216.（in Chinese））

[22] Salisbury J I，Wimbush M.Using modern time series analysis techniques to predict ENSO events from the SOI time series[J].Nonlinear Processes in Geophysics，2002，9（3/4）：341-345.DOI：10.5194/npg-9-341-2002