日径流序列混沌识别中合理长度的确定

周长让+陈元芳+顾圣华+黄琴

摘要：混沌理论是进行水文时间序列分析的重要手段。为保证分析结果的可靠，主张充分利用现有资料，但目前缺乏时间序列长度对混沌特性识别影响的研究。以长江上游武隆站和北碚站日径流序列（1951年-2012年）为例，通过对二者进行混沌分析，研究了最大Lyapunov指数对序列长度的响应。结果表明，日径流时间序列长度过小时会影响混沌识别结果，使结果缺乏可靠性；并不是样本序列长度越长混沌识别结果越好；当序列长度达到3 000左右时，序列的混沌特性达到稳定，结果可靠并缩短了计算时间。

关键词：水文时间序列分析；日径流时间序列；时间序列长度；混沌识别；饱和关联维数；最大 Lyapunov指数；混沌特性

中图分类号：TV121文献标志码：A文章编号：1672-1683（2017）01-0055-05

Abstract：Chaotic theory is an important means of hydrology time series analysis.In order to get reliable analysis results，it is recommended to make a full use of time series.But the research about how the length of time series affects the identification of chaotic characteristics is rare.In this paper，we carried out a study about the responding effect of the maximum Lyapunov exponent to the length of time series with the use of daily runoff time series of gauged stations named Wulong and Beibei in Yangtze River.The result suggested that short daily runoff time series would affect the result of chaotic identification and make the result unreliable；besides，when the length of daily runoff time series reached 3 000，the chaotic characteristics became stable and reliable，and it saved a lot of computing time at the same time.

Key words：hydrology time series analysis；daily runoff time series；the length of time series；chaotic identification；saturated correlation dimensions；the maximal Lyapunov exponents；chaotic characteristics

流域的徑流过程的研究方法和手段有很多：基于物理基础的水文模型、随机水文时间序列分析方法、人工神经网络、模糊集、模糊逻辑、模糊神经、遗传算法、以及混沌等[1]。混沌现象存在于诸多研究领域，包括天文学、生物学、化学、生态学、工程学以及物理学等[2]。混沌科学是非线性科学的一个重要分支，同时是解决非线性问题的重要工具。水文现象是一种具有非线性规律的自然现象，以往的研究结果表明水文时间序列中存在混沌现象，因此探究水文序列的混沌特性对深入了解水文规律具有重要意义。关于利用混沌理论进行水文时间序列分析，已经有若干进展。李国良[4]利用混沌理论，系统而全面地对时间序列的混沌分析方法进行了介绍。楼玉[5]建立了腾龙桥站日径流和兰溪站月径流的混沌径流预报模型，模型预报结果良好。牟丽琴[6]等则对汀江流域的月降雨混沌序列进行了混沌识别。袁鹏[7]等证明了四川省6个水文站的月降雨量时间序列可能存在混沌现象。周寅康[8]等对淮河流域的洪涝序列进行了混沌识别，并确定了该时间序列的最大可预报时间长度。但是针对时间序列长度对序列混沌特性识别的影响，研究甚少。此外，在进行相空间重构时，考虑到不同序列长度所需要的计算时长不同，序列的混沌特性随着序列长度的变化的规律也尚不清晰。因此探究时间序列长度与最大Lyapunov指数之间的关系，对合理选择序列长度、混沌识别可靠性及减少计算工作量具有重要意义。

1 混沌识别与最大Lyapunov指数的计算

1.1 混沌识别

混沌是非线性动力系统所特有的一种运动形式，它是既普遍存在又极具复杂性的现象[9]。混沌现象是貌似无序中的有序，是确定的映射中的类随机性[10]。混沌理论在进行时间序列分析时可分为混沌识别和混沌预测。混沌识别先对水文时间序列进行相空间重构，继而在高维空间中识别其混沌特性；混沌预测主要是结合混沌识别与水文预测模型，对水文序列未来可能的变化进行预测。

混沌识别的主要步骤为：（1）相空间重构（自相关函数法确定延迟时间；饱和关联维数法同时确定混沌序列的最小嵌入维数和饱和关联维数）；（2）混沌特性的定量识别（Wolf方法确定序列的最大Lyapunov指数）。

1.2 方法介绍

1.2.1 自相关函数法确定延迟时间

自相关函数描述了序列在第i时刻和第i+τ时刻，运动的相似程度。一般而言，时间间隔τ越小，xi和xi+τ的相似程度越高，r（τ）也就越大。对于时间序列{x1，x2，…，xn}，自相关函数可以表示为：

实际工作中，延迟时间的选取不宜过大和过小[11]，因此应根据自相关函数，选择合适的延迟时间τ。一般选择自相关函数首次经过零点时对应的时间为延迟时间；但当自相关函数首次取零时的延迟时间过大，则可以减小相空间重构的时间移动值，选择自相关函数下降趋于稳定时对应的时间为延迟时间。

1.2.2 Wolf方法计算最大Lyapunov指数

衡量动力系统对初始条件敏感依赖性的一个重要指标就是Lyapunov指数[12]。Lyapunov指数是混沌现象的定性和定量的特征参数，它表现为相点在相空间中的相邻轨道之间以指数形式快速分离或者收敛[13]。假设空间中有两个相点xi和xj，两点间的初始距离为d0=‖xi-xj‖，在系统演化τ时段后，两点间的距离为dk=‖xi+τ-xj+τ‖，如果dk≈d0eλτ，即两点间距离呈指数分离，其中λ就是最大Lyapunov指数[13]。对于最大Lyapunov指数的计算，常用Wolf方法估计。计算公式如下：

式中：l为向量个数；τ为延迟时间；Di为重构的相空间里两个相点之间的最小欧氏距离；λ为最大Lyapunov指数，其他参数意义同前。当最大Lyapunov指数大于0时，可以判断出序列可能为混沌序列，且最大Lyapunov指数的取值越大，序列的混沌特性越明显。

2 实例研究

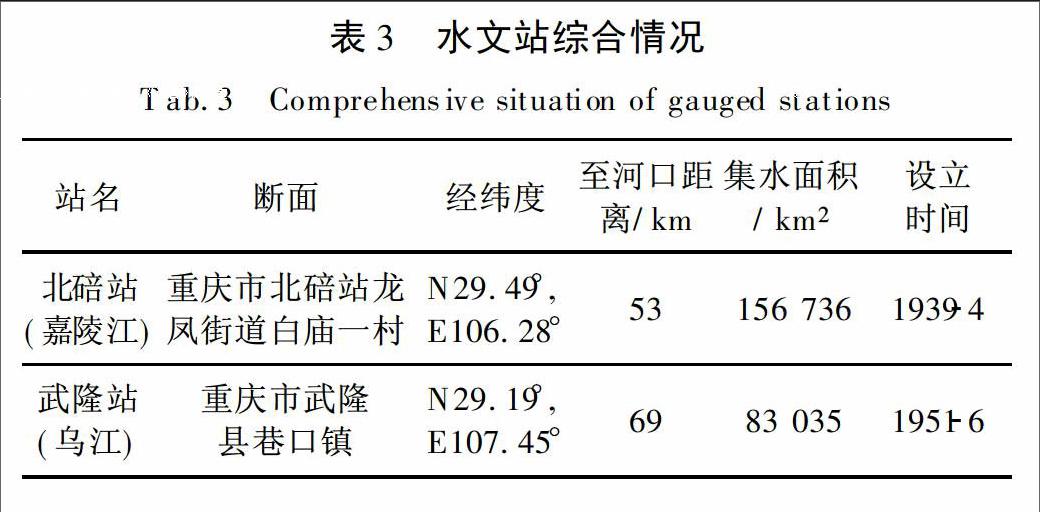
本文以长江流域的武隆站和北碚站历年逐日径流时间序列为例，对时间序列长度与水文序列的混沌特性进行研究。为了进行相似水文背景下的研究，选取两个水文站1951年-2012年的日平均流量序列作为研究对象。

2.1 自相关函数法确定延迟时间

根据以上所介绍的自相关函数法，利用已有的日径流资料绘制出给定时间移动值τ下的自相关函数。在实际计算和绘图过程中，为防止延迟时间选择的不合理，分别采用τ=1 000与τ=100绘制了两组自相关函数曲线，以便于对比分析。结果表明，两个水文站在τ=1 000时自相关函数曲线首次经过零点时所对应的延迟时间均在80～100之间，明显偏大，因此不予考虑。从而主要取τ=100时自相关曲线变化趋于平缓所对应的时间，作为序列相空间重构的延迟时间。两个站日径流时间序列的自相关曲线见图1、图2。计算结果表明，武隆站日径流时间序列的延迟时间τ0为10，北碚站日径流时间序列的延迟时间τ0为4。

2.2 饱和关联维数法确定日径流时间序列的嵌入维数和饱和关联维数

实例研究中，根据以上所介绍的饱和关联维数法，取不同的嵌入维数m对原序列进行相空间重构，得出对应维数下的饱和关联维数D2（m），最后建立嵌入维数m与饱和关联维数D2（m）之间的关系曲线，取曲线达到稳定时对应的嵌入维数和饱和关联维数。图3和图4中的（a）图，自上而下为m取2，3，…，12时对应的饱和关联维数曲线，（b）图为饱和关联维数随嵌入维数变化曲线。

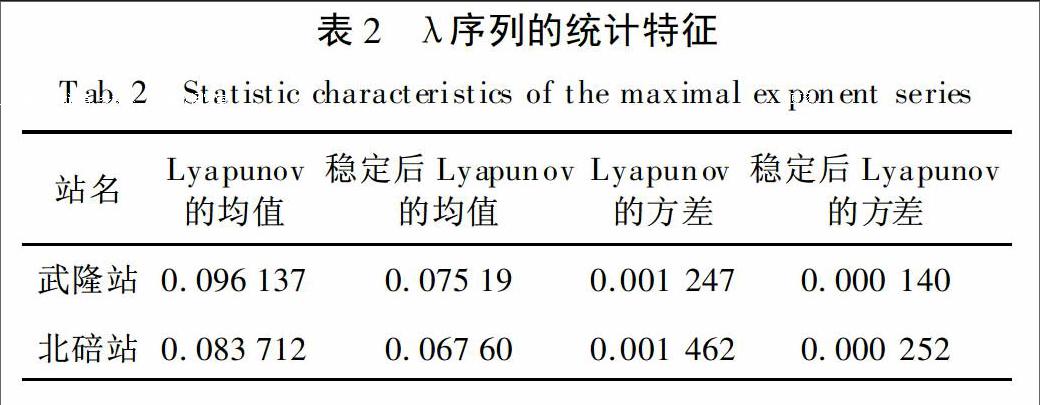
图3、图4对应的计算结果见表2。从表2可以得出，两个水文站的关联维数在有限的数据长度下，随着嵌入维数的升高，均表现出了趋于饱和的现象，因此两个水文站的水文时间序列可能为混沌序列。

王文等[14]指出，在进行混沌分析也不一定需要数千、数万个点的时间序列，在维数不高的情况下，有500个点左右的长度基本满足要求。由于研究对象为日径流时间序列，且混沌识别时的嵌入维数均较高，因此序列长度（记为L）应尽量长。以往研究已证明水文现象普遍具有混沌特性。但是当L在100以内时，时间序列并不表现出混沌特性（如北碚站的最大Lyapunov指数为-123.8）。因此，使用较少的时间序列进行混沌识别和预测缺乏准确性、可靠性。

在实际计算过程中，当L从100增加到6 000的过程中，计算时间由不到1 s增加到20 min以上（1 200 s），计算时间随着计算长度的增加呈近似指数的增长。而随着L的增加，时间序列的混沌特性逐渐达到稳定，从而选择合适的L不仅可以保证结果的可靠性，而且可以大大缩短计算时间。

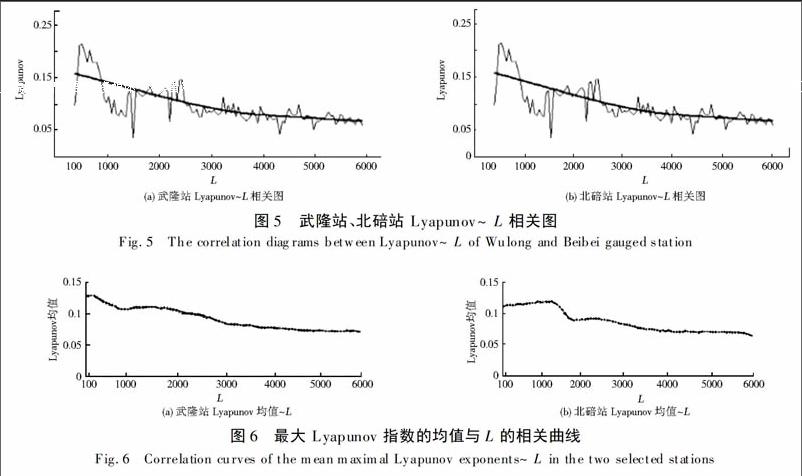
根据不同时间步长所获得的最大Lyapunov指数（简称Lyapunov），绘制Lyapunov与L相关曲线图（见图5）。其中，图中的曲线为局部二阶多项式回归所对应的趋势线。从图5中可以看出在L较小时，样本对总体的代表性较差，因此曲线波动较大。之后，随着L的增加，武隆站的Lyapunov先是表现出明显的减小趋势，随后趋于稳定；北碚站的Lyapunov随着L增加，曲线始终波动较为平缓，最终达到稳定，Lyapunov的取值也趋于稳定。对Lyapunov进行滑动平均的均值，并绘制相关曲线，见图6。

由图6（a）图和（b）可知，当L=3 000时，时间序列的Lyapunov基本达到稳定。

为了比较时间序列混沌特性的强弱，对所选取的两个水文站的Lyapunov序列稳定前后的统计特性进行了分析，结果见表2。从表2可以看出武隆站的Lyapunov大于北碚站的，换而言之，武隆站日徑流时间序列的混沌特性更强。此外，武隆站的Lyapunov序列随时间序列长度的波动相对较小，混沌特性变化较小，而北碚站的Lyapunov随时间长度的波动较大，混沌特性波动较小。

王亦农[15]指出“水文水资源系统具有产生混沌的基本条件—对初始条件的敏感性和内在的随机性。对于同一水文系统，不同的边界条件会产生完全不同的水文过程。” 换而言之，对于同一场暴雨过程，由于两个站点的位置不同，二者的水文过程也大相径庭。借此，对以上结果（武隆站的Lyapunov指数大于北碚站）进行分析可知，武隆站对初值的敏感性更强，内在的随机性也更强。影响时间序列混沌特性的因素众多，若从水文站点所在流域特征来说，嘉陵江流域的集水面积相对乌江更大，调蓄能力较强，其对初始条件的敏感性相对于乌江更弱。从而武隆站日径流时间序列的Lyapunov指数较大，因此混沌特性相对较强，而北碚站则较弱。

4 结论

通过对实例中的武隆站和北碚站1951年-2012年日平均流量资料序列进行混沌分析和相应的计算结果可以得到如下结论。

（1）从混沌特征角度。（a）饱和关联维数随着嵌入维数的升高呈现出趋于饱和的现象；（b）最大Lyapunov指数均大于0，体现了序列对初值具有很强的敏感性。因此这两个序列具有混沌序列的基本特征，从而两个时间序列可能为混沌序列。

（2）从最大Lyapunov指数的统计特性角度。（a）武隆站日径流时间序列的最大Lyapunov指数较大，因此混沌特性相对较强，而北碚站则较弱；（b）武隆站日径流时间序列的混沌特性随时间序列长度的增加波动较大，北碚站的变化较小；

（3）从序列长度角度。日径流时间序列长度过小时样本的混沌分析结果的可靠性降低，从而在资料长度允许条件下，尽量使用较长的时间序列；对于长度较长的序列，进行混沌分析时并非长度越长越好，资料长度过长往往计算需要较长的计算时间，甚至超出计算内存。从实例研究的结果来看，当序列长度达到3 000左右时，序列的混沌特性达到稳定，且结果可靠、计算时间相对较少。从而，选择合适的序列长度可以在减少工作量的同时，得到代表性较好而稳定的结果。

参考文献（References）：

[1] Rahman Khatibi，Bellie Sivakumar，Mohammad Ali Ghorbani，et al.Investigating chaos in river stage and discharge time series[J].Journal of Hydrology，2012，414-415：108-117.

[2] W W Ng，U S Panu，W C Lennox.Chaos based analytical techniques for daily extreme hydrological observations[J].Journal of Hydrology，2007，342：17-41.

[3] 李國良.混沌理论及其在水文时间序列中的应用研究[D].哈尔滨：东北农业大学，2007.12.（LI Guo-liang.Studies on chaos theory and its application in hydrology time series[D].Harbin ：Northeast Agriculture University，2007.12.（in Chinese）

[4] 楼玉.混沌时间序列方法在径流预报中的应用研究[D].杭州：浙江大学，2005.8.18.（LOU Yu.Chaotic time series methods in the study of the application of the runoff forecast[D].Zhejiang Hangzhou Zhejiang University，2005.8.18.（in Chinese）

[5] 牟丽琴，林焕新.汀江流域降水时间序列的混沌分析[J].人民珠江，2010（01）：27-29，55.（MOU Li-qin，LI Huan-xin.Chaotic analysis of rainfall time series in Tingjiang catchment[J].Pearl River，2010（01）：27-29，55.（in Chinese）

[6] 袁鹏，李谓新，王文圣，等.月降雨量时间序列中的混沌现象[J].四川大学学报：工程科学版，2002，34（1）：16-19.（YUAN Peng，LI Wei-xin，WANG Wen-sheng，et al.Chaos analysis of monthly precipitation time series[J].Journal of Sichuan University：Engineering Science Edition，2002，34（1）：16-19.（in Chinese）

[7] 周寅康，王腊春，张捷.淮河流域洪涝变化的混沌特征[J].自然灾害学报，1999，8（1）：42-47.（ZHOU Yin-kang，WANG La-chun，ZHANG Jie.Some chaotic characteristics of the flood series in Huai River basin[J].Journal of Natural Disasters，1999，8（1），42-47.（in Chinese）

[8] 李新杰.河川径流时间序列的非线性特征识别与分析[D].武汉：武汉大学，2013.3.（LI Xin-jie.Nonlinear characteristics identification and analysis for river runoff time series[D].Wuhan：Wuhan University ，2013.3 .（in Chinese）

[9] 陈关荣，吕金虎.Lorenz系统族的动力学分析、控制与同步[M].北京：科学出版社，2003.（CHEN Guan-rong，LYU Jin-hu.Dynamics analysis、control and synchronization of Lorenz system[M].Beijing：Science Press，2003.

[10] 王文，许武成.混沌时间序列可预报时间长度分析[J].河海大学学报：自然科学版，2004，32（4）：367-371.（WANG Wen，XU Wu-cheng.Analysis of length of predictable time of chaotic time series[J].Journal of Hohai University ：Natural Sciences，2004，32（4）：367-371.（in Chinese）

[11] 袁鹏，李谓新，王文圣，等.月降雨量时间序列中的混沌现象[J].四川大学学报：工程科学版，2002，34（1）：16-19.（YUAN Peng，LI Wei-xin，WANG Wen-sheng，et al.Chaos analysis of monthly precipitation time series[J].Journal of Sichuan University ：Engineering Science Edition，2002，34（1），16-19.（in Chinese）

[12] Alan Wolf，Jack B Swift，Harry L Swinney，et al.Determining Lyapunov exponents from a time series[J].Physica 16D，1985，285-317.

[13] Lorenz，Edward N.Dimension of weather and climate attractors[J].Nature，1991，353（6341）：241-244.

[14] 王文，许武成.对水文时间序列混沌特征参数估计问题的讨论[J].水科学进展，2005，16（4）：609-616.（WANG Wen，XU Wu-cheng.Some issues on the characteristics of chaotic properties of hydrologic time series[J].Advances in Water Science，2005，16（4）：609-616.（in Chinese）

[15] 王亦农.浅谈混沌与水文[J].资源环境，2011，3（40）：71-72.（WANG Yi-nong.A brief talk about chaotic and hydrology[J].Resources and Environment，2011，3（40）：71-72.（in Chinese）