基于LM和SVD结合的点云拼接算法研究

吴晓庆, 黄玉清

(西南科技大学信息工程学院，四川 绵阳 621010)

基于LM和SVD结合的点云拼接算法研究

吴晓庆, 黄玉清

(西南科技大学信息工程学院，四川 绵阳 621010)

点云拼接是场景三维重建过程中的重要环节。针对现有的拼接算法存在耗时长、拼接效果差等问题，通过利用正交映射，获取三维点云与二维图像之间的映射关系，并在二维图像中获取匹配点对。在此基础上，提出了采用LM和SVD结合的方法来变换矩阵。首先根据正交映射，获取三维点云所对应的二维图像；其次利用SURF算法，提取图像的特征点，并通过FLANN算法以及RANSAC算法，提取两幅图像中的特征拼接点对；最后将LM和SVD两种方法相结合，求得变换矩阵。试验结果表明，无论拼接精度，还是运行速度，该算法均较直接利用LM算法或SVD算法有所提高。

机器人; 点云拼接; 正交映射; 线性最小二乘法;LM算法;SVD算法; 变换矩阵

0 引言

随着机器人技术的发展，其应用领域也不断扩展，现在已经可以代替或者辅助人类完成很多艰巨的任务[1]。面对未知的环境，比如核辐射环境、太空等，要想实现对这些环境的识别，就必须要对机器人所“看到”的场景进行重建；而拼接又是重建过程中非常重要的组成部分。由于现实中摄像头视场角度固定，很难一次性获得场景的完整信息[2]，所以我们更加需要对获取的三维图像进行拼接。

迭代最近点(iterationclosestpoint，ICP)算法是三维点云广泛使用的方法。该算法只针对两个点云集初始相对位置已知的情况；当两个点云的重合部分比较少时，该算法容易陷入局部最优值[3]。而且，当点云非常大时，运算速度就会非常慢且精度也不高。所以如何提高三维点云的匹配精度和速度的难题，一直困扰着我们。相对于三维点云拼接，二维图像的拼接方法则相对成熟。例如尺度不变特征变换(scaleinvariantfeaturetransform，SIFT)算法，该算法对图像的旋转、尺度缩放、亮度变化等保持不变[4]；加速鲁棒特征(speededuprobustfeatures，SURF)提取算法[5]，对外界具有很强的鲁棒性。因此，利用二维图像提取特征点，完成点云的拼接，为拼接提供了一个新的思路[6]。而在基于图像特征的点云拼接中，也常利用随机抽样一致性(randomsampleconsensus，RANSAC)[7-8]算法鲁棒优化，去除不可靠的匹配点对，同时结合奇异值分解(singularvaluedecomposition，SVD)[9-16]来获取转换矩阵。

而在点云拼接求取变换矩阵过程中，列文伯格-马夸尔特法(levenbergmarquardt，LM)却很少被人使用，该算法是最优化算法中的一种，具有高斯-牛顿法的局部收敛性和梯度下降法的全局特性，局部搜索能力非常强[12]。所以，本文在JuanLi[7]工作的基础上，利用正交投影，获得三维点云与二维图像间转换，将SURF、快速最近邻算法(fastlibraryforapproximatenearestneighbors，FLANN)[9]以及RANSAC相结合提取特征点对。求取变换矩阵时，结合LM和SVD算法，最终实现点云的拼接。

1 算法描述

基于LM和SVD结合的点云拼接算法的基本思路是：首先利用正交映射将无序的彩色点云映射成二维图像；然后利用SURF算法完成二维图像的特征提取，并利用FLANN中KD-TREE快速搜索对特征点进行匹配，利用RANSAC算法删除错误特征匹配点；根据三维与二维之间的映射关系，将二维图像中的特征点对映射到三维点云中，获取两点云之间的特征点对；最后结合LM和SVD算法，通过特征点对获取点云之间的变换矩阵，完成点云的拼接。算法流程图如图1所示。

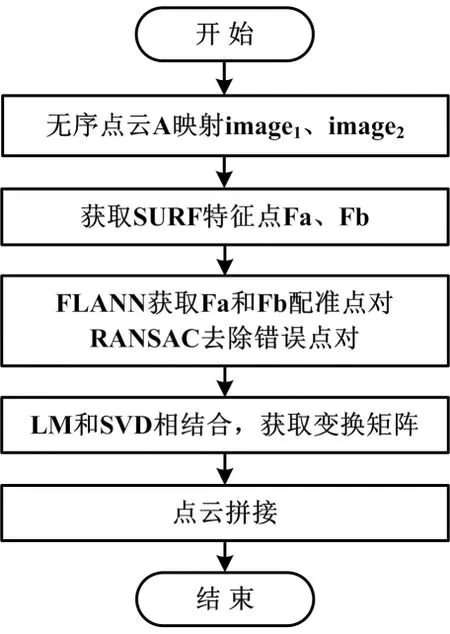
图1 算法流程图

1.1 3D-2D的正交投影

(1)正交投影。

投影线垂直于投影面的投影属于正交投影，也称平行投影。设I与Z分别为具有二阶矩的n维和m维随机向量，如果存在一个与I同维的随机向量&Icri满足下列条件：①线性表示&Icri=A+BZ；②无偏性，E(&Icri)=E(I)；③正交，E[(I-&Icri)ZT]=0，则称&Icri是I在Z上的正交投影(注：把矩阵Z的行换成相应的列，得到的新矩阵称为Z的转置矩阵，记为ZT)。

(2)三维与二维之间的映射。

计算位于OXYZ坐标系统的平均法向量，并且选择平行于Z轴的法向量，三维(3D)平面就可以通过正交投影，映射到XOY的二维(2D)平面上。在3D坐标系统中，表面法向量可以被视为在表面上点的平均法向量[7]。令表面法向量为V(x,y,z)T和|V|=1，定义旋转矩阵为：

(1)

(2)

则很容易证明：

(3)

向量(0,0,1)T是平行于Z轴的法向量。将点云中的每一个点都进行旋转，可以得到一个新的表面，而这个新表面的法向量平行于Z轴。新表面的点Xnew和在原始点云上的点Xcloud之间的关系为：

(4)

3D表面和2D图像的正交投影关系如图2所示。

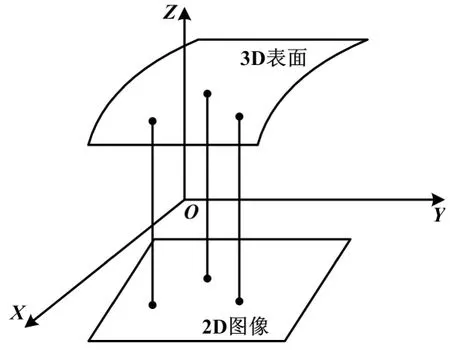
图2 3D表面和2D图像的正交投影关系示意图

1.2 特征提取

(1)SURF特征点提取。

本文使用SURF算法提取特征点。虽然SIFT算法比较稳定，检测到的特征点也比较多，但是其最大的缺点是计算复杂度较高。有很多学者对其进行了改进，如SIRF算法。SURF构造的金字塔图像与SIFT有很大不同。SIFT采用的是DOG图像，而SURF采用的是Hessian矩阵行列式近似值图像[10]。

SURF算法的基本思路是利用积分图像和盒子滤波建立尺度空间，使用Hessian矩阵进行特征点检测，并使用Haar小波分析提取特征点的描述符[10]。它主要有以下五个步骤：①构建Hessian矩阵，该矩阵是SURF算法的核心；②构建尺度空间，图像的尺度空间是该图像在不同解析度下的表示；③精确定位特征点，在这个过程中，所有小于预设极值的取值都被丢弃，增加极值使检测到的特征点数量减少，最终只有几个特征最强的点会被检测出来；④主方向确定；⑤特征点生成。

(2)FLANN与RANSAC结合获取匹配点对。

由于噪声、计算误差等外界因素的影响，仅仅使用FLANN查找到的相应点存在误匹配的情况，所以我们使用FLANN算法和RANSAC算法相结合的方式，来获取较为准确的匹配特征点。通过FLANN算法，获取特征点的初始匹配；进一步删除错误匹配点；最终获取更加准确的匹配点对。

1.3 变换矩阵求取

(1)LM算法。

LM算法是一种基于目标函数的微分迭代技术，现已成为求解非线性最小二乘法问题的标准方法，可以视为梯度下降法和Gauss-Newton法的结合[11]。LM算法的实现并不困难，其关键是用模型函数f对待估参数向量p在其领域内作线性近似，忽略二阶以上的导数项，从而转换为线性最小二乘法问题，具有收敛速度快等优点[12-14]。

LM算法是一种“信赖域法”。假设一个可以信赖的最大位移，以当前点为中心，在以最大位移为半径的区域内搜索目标函数的一个最优点的近似，从而求得真正的位移。在得到位移后，再次计算目标函数值。如果该目标函数值的下降满足一定条件，说明这个位移是对的，则按照此步骤迭代下去；如果不能满足条件，则应该减小信赖域区域，重新求解。

(2)SVD算法。

奇异值分解是线性代数中一种重要的矩阵分解。矩阵奇异值分解的具体步骤和过程[13]如下。

①计算矩阵AHA的特征值λ1≥λ2≥…≥λr>λr+1=…λn=0。

②计算特征值对应的特征向量，并组成正交矩阵V：

(5)

③将V写成分块矩阵：

(6)

④计算U1：

U1=AV1∑-1

(7)

⑤将U1扩充为酉空间Cm的标准正交基，组成m阶有矩阵U：

U=[U1U2]

(8)

⑥于是酉矩阵的奇异值分解为：

(9)

(3)LM和SVD的结合算法。

通过分别使用LM和SVD方法，对获取的特征点对求取变换矩阵，最终完成点云拼接；然后通过式(10)，获取最终的变换矩阵。

[RT]=α[RtmTtm]+(1-α)[RsvdTsvd]

(10)

式中：α为权重。经过反复测试，发现当权重是50%时，所取得的效果最佳。

权重分析如表1所示。

表1 权重分析

2 试验结果

试验平台硬件环境为：深度摄像头微软kinect，软件开发工具为Windows 7操作系统，vs2012，pcl 1.7.2，opencv 2.4.9。在同一个平台下，对比了两种算法的拼接时间和拼接误差。试验结果及分析如下。

①场景拼接。

针对点云的拼接效果，使用拼接误差E来描述[16]，计算公式如下：

E=Er/Cr

(11)

式中：Er为所有有效拼接点对的距离误差总和;Cr为有效凭借点对数。

②结果分析。

在点云拼接过程中，记录了程序运行的拼接时间以及三种算法的拼接误差，如表2所示。

表2 三种算法对比

三种算法都是在相同的平台下作同样的工作。可以看出，本文算法的运行时间和拼接误差都是三种算法中最优的。

3 结束语

针对现在点云拼接算法中存在的拼接速度慢、特征拼接效果差的问题，运用三维映射到二维的正交映射，结合SURF特征提取、FLANN算法以及RANSAC获取更加准确的匹配点对后，提出了采用LM和SVD相结合的算法，来获取两点云之间的变换矩阵，实现点云拼接的目的。

相较于通过传统的ICP算法获得变换矩阵，本文算法的耗时更短。在不影响拼接效果的前提下，点云的拼接速度得到了提高。试验表明，本文提出的算法在拼接效果、速度方面表现非常好。

下一步改进方向为以下两方面：①考虑将点云滤波加入算法，来滤除点云中的干扰项；②考虑在实现三维点云拼接的基础上，实现多角度的全局拼接。

[1]BERTOZZIM.Vision-basedintelligentvehicles:stateoftheartandperspectives[J].Robotics&AutomationSystems,2000,32(1):1-16.

[2] 储珺,聂春梅,王璐.基于SIFT特征的多视点云数据配准和拼接算法[J].半导体光电,2011,32(3):442-447.

[3]HELL,WANGS,PAPPASTN.3DSurfaceregistrationusingZ-SIFT[C]//IEEEIntrenationalConferenceonImageProcessing,2011:1985-1988.

[4] 王程冬,程筱胜,崔海华,等.SIFT算法在点云配准中的应用[J].传感器与微系统,2012,31(2):149-152.

[5]LUOJ,GWUNO.SURFappliedinpanoramaimagestitching[C]//2ndInternationalConferenceonImageProcessingTheoryToolsandApplications,2010:495-499.

[6] 张晓,张爱武.基于图像的点云初始配准[J].计算机工程与设计,2014,35(10).

[7]LIJ,JIANGG.Pointcloudsregistrationwithsurfacesoflowcurvatures[C]//2015IEEEInternationalConferenceonSignalProcessing,CommunicationsandComputing(ICSPCC),2015:1-5.[8] 常青,张斌,邵金玲.基于SIFT和RANSAC的特征图像匹配方法[J].华东理工大学学报,2012,38(6):747-751.

[9]MUJAM,LOWEDG.Fastapproximatenearestneighborswithautomaticalgorithmconfiguration[C]//ProceedingsofIEEEConferenceonComputerVisionTheoryandApplications.Lisbon,Portugal:IEEEComputerSociety,2009:331-340.

[10]毛星云,冷雪飞,王碧辉,等.OpenCV3编程入门[M].电子工业出版社,2015:396-400.

[11]文成哲,刘财,郭智奇,等.遗传算法和LM算法联合反演锐雷波相速度[J].地球物理学进展,2010,25(1):303-309.

[12]张长胜,欧阳丹彤,岳娜,等.一种基于遗传算法和LM算法的混合学习算法[J].吉林大学报,2008,46(4):675-680.

[13]鲁铁定,宁津生,周世键,等.最小二乘配置的SVD分解解法[J].测绘科学,2008,33(3):47-51.

[14]张玉涛,李亚清,邓军,等.煤炭自然灾害过程突变特性研究[J].中国安全科学学报,2015,25(1):78-84.

[15]CHUMO,PHILBINJ,ZISSERMANA.Nearduplicateimagedetection:minhashandweighting[C]//Proceedingsofthe19thBritishMachineVisionConference,London,UK,2008:493-502.

[16]左超,鲁敏,谭志国,等.一种新的点云拼接算法[J].中国激光,2012,39(12):1-8.

ResearchonthePointCloudStitchingAlgorithmBasedonCombinationofLMandSVD

WUXiaoqing,HUANGYuqing

(SchoolofInformationEngineering,SouthwestUniversityofScienceandTechnology，Mianyang621010,China)

Pointcloudregistrationisanimportantroleinthereconstructionof3Dscenes.Aimingattheproblemsexistingincurrentregistrationalgorithms,suchastime-consumingandpoorregistrationeffect,throughadoptingorthogonalmapping,themappingrelationsbetween3Dpointcloudand2Dimageisobtained,andthematchingpointpairsarecapturedin2Dimage.Onthisbasis,bycombininglevenberg-marquardt(LM)algorithmandsingularvaluedecomposition(SVD),thematrixistransformed.Firstly,inaccordancewiththeorthogonalmapping,the2Dimagecorrespondingtothe3Dpointcloudisacquired;thentheimagefeaturepointsareextractedbyusingSURFalgorithm,andwithFLANNalgorithmandRANSACalgorithm,thesplicingpointpairfortwoimagesisextracted;finally,thetransformationmatrixisobtainedbycombiningtheLMandSVD.TheresultsofthetestsindicatethatthemethodproposedgetsbettersplicingaccuracyandrunningspeedthenthosebyLMalgorithmorSVDalgorithm.

Robot;Pointcloudsregistration;Orthogonalmapping;Linearleastsquaremethod;LMalgorithm;SVDalgorithm;Transformationmatrix

国家自然科学基金资助项目(61401379)、国防应用技术项目资助(12zg610303)

吴晓庆(1991—)，女,在读硕士研究生，主要从事图像处理与机器视觉的研究。E-mail:1253742950@qq.com。黄玉清(通信作者)，女，硕士，教授，主要从事无线控制及无线通信技术、图像处理与机器视觉、智能技术的研究。E-mail:hyq_851@163.com。

TH-3;TP

ADOI: 10686/j.cnki.issn1000-0380.201701008

修改稿收到日期:2016-07-27