基于互补滤波的输电导线舞动轨迹还原算法

汪 滔，吴德智，胡 柯，孔海林， 李 睿

(1. 国网浙江省电力公司 温州供电公司，浙江 温州 325000；2. 北京国网富达科技发展有限责任公司，北京 100070)

基于互补滤波的输电导线舞动轨迹还原算法

汪 滔1，吴德智1，胡 柯1，孔海林1， 李 睿2

(1. 国网浙江省电力公司 温州供电公司，浙江 温州 325000；2. 北京国网富达科技发展有限责任公司，北京 100070)

方向余弦矩阵算法(DCM算法)是工业级MEMS惯性传感器姿态解算常用算法;但由于受到外部机械振动和电磁环境影响，MEMS陀螺仪输出数据的漂移较大，导致陀螺积分解算得出的姿态角误差会随着时间累积增长，因此常须结合DCM算法与GPS或磁罗盘对陀螺计算出的角度进行误差修正;然而电网的导线舞动监测仪是直接安装于高电压架空输电线路表面，仪器处于很强的工频电磁干扰环境中，GPS和磁罗盘传感器完全失效，所以若要实现实时准确输出高压导线的运动轨迹，有必要研究一种改进的DCM算法，即MEMS陀螺和加速度计的互补滤波算法；并且设计出高电压导线舞动轨迹适用的解算流程，最后在专用的舞动监测实验平台上验证此新型舞动监测仪样机的有效性。

导线舞动；互补滤波；加速度计；陀螺仪

0 引言

我国电网在随着国民经济增长而快速发展的同时，也频遭到气象灾害的袭扰，高压输电导线的舞动是常见的灾害之一。舞动是在特定的气象条件下，综合了风力、覆冰翅升力、架空导线张力等诸多合力而发生在输电导线上的一种大振幅、低频率的机械振动。舞动的全过程包括起舞、维持、衰减阶段。架空导线覆冰舞动就是发生频率高、影响范围广、造成损失大的一种灾害形式[1-3]。大范围的输电线路舞动，导线舞动造成多处导线烧伤或断股、导线间隔棒掉抓或损坏、螺栓松动、金具断裂、铁塔腿基保护帽破裂，严重时可能导致倒塔事故，给电网的运行安全带来了极大的隐患。为了及时掌握架空输电线路的运动变化情况，须在易舞区相关线路上部署导线舞动在线监测系统，实时采集舞动因素的数据。继而，数据传输至后台运行中心的在线监测专家系统，为舞动机理理论研究、防舞装置的研发以及防舞有效预警提供必要的技术支持[4]。

导线舞动监测仪是直接安装于高电压架空输电线路表面，仪器时刻处于很强的工频电磁干扰环境中，GPS或磁罗盘传感器失效，所以为了实时准确输出高压导线的运动轨迹，本文提出采用改进的方向余弦矩阵(direction cosine matrix, DCM)算法，即MEMS陀螺和加速度计的互补滤波算法。根据导线舞动轨迹的不规则圆周特性，可以只选用MEMS陀螺和加速度计的方案来计算俯仰和滚转角，不用考虑航向角。因而采用的是改进的DCM算法，即MEMS陀螺和加速度计的互补滤波算法[5]。一方面，采用MEMS陀螺输出的角速度通过积分解算得到姿态角，但由于周围环境以及MEMS传感器自身的原因，角速度计积分出来的角度误差会随时间累积，长时间可能引起严重的角度偏移；另一方面，根据加计的输出计算出物体在重力场中的倾角，这种计算倾角的方法虽然易受物体运动加速度的影响，但没有累积误差，尤其当物体加速运动不是很显著的情况下精度较高，可以用来对角度进行纠正。所以这两个传感器正好可以弥补相互的缺点。本文给出导线舞动监测仪工作流程和主要的硬件传感器配置。以仿真测试验证该算法的正确性，并且搭建模拟导线舞动的特殊实验测试平台，对舞动监测方案可行性和仪器的数据准确性进行了测试。

1 舞动监测仪总体结构设计

为了实现在线监测导线舞动的幅值和频率等轨迹信息。本导线舞动的监测仪采用陀螺仪与加速度计组合的惯性传感器为主要监测元件，搭载STM32低功耗系列处理器芯片，实现高精度、低功耗舞动在线监测[6]。工作过程中舞动监测仪通过一段时间的采集，再由数据积分运算完成该点运动轨迹的还原，为了即时掌握整体线路的舞动情况，须引入适当的惯导系统的重力校准方法[7]。舞动装置数据采集流程如图1所示。

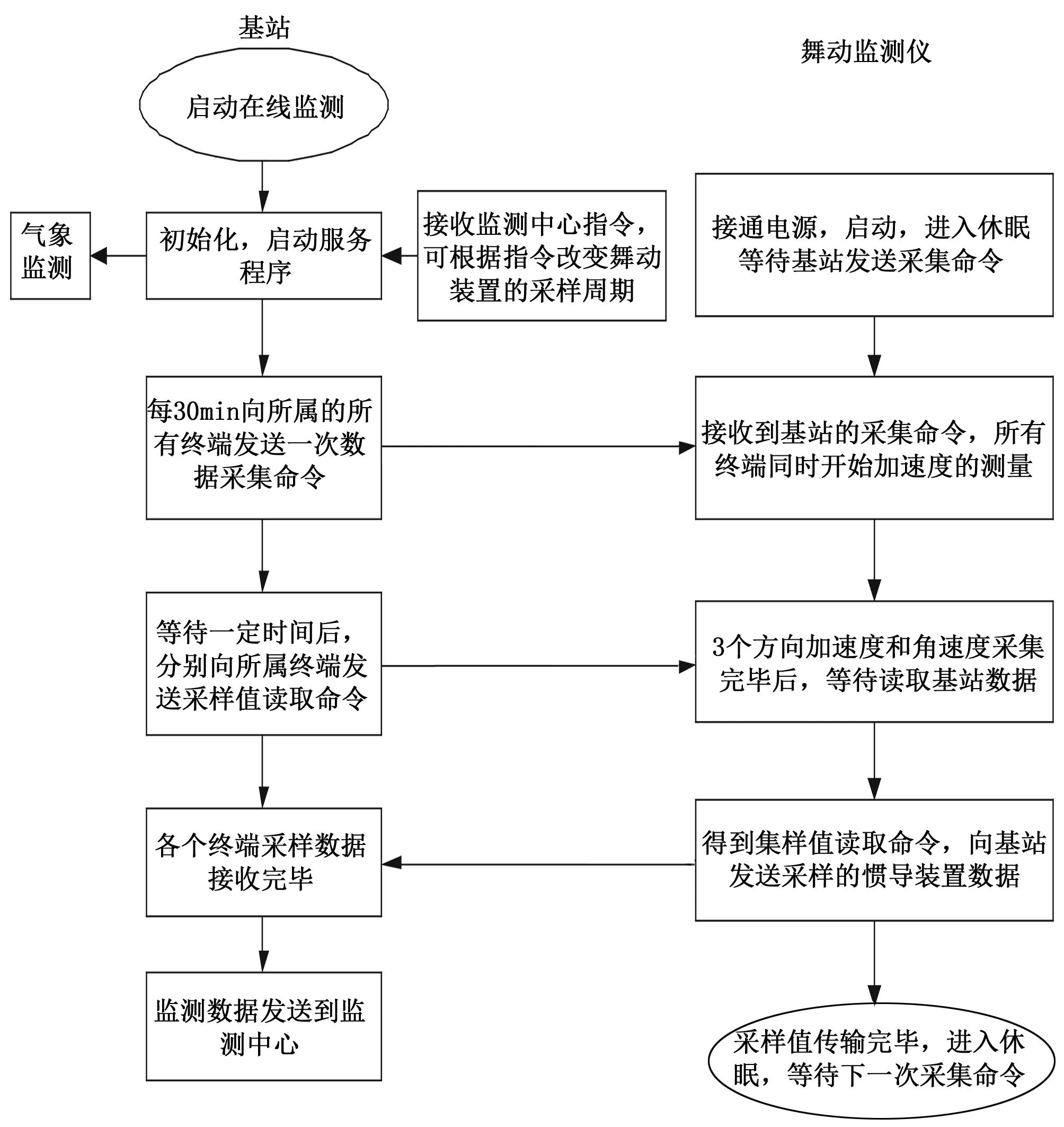
图1 舞动监测系统的数据采集流程图

舞动监测仪数据采集的要求如下：

1)通信同步性要求：为了达到多个监测仪的运算结果来分析一条线路运行轨迹的要求，刚这此采集点的采集必然要有同步性的要求，以及多次测量的要求。要安装多个监测点的采集的同步性，保证每个点3个方向采集的同步性，同时要保证多个监测点采样的同步性(同步误差应小于20 ms)。所以本文采用Zigbee方式组建在线监测的无线通信网络[8]。

2)采集频率以及采样点数要求：采样要满足舞动频率0.1～3 Hz的要求，每个监测点采样至少2个舞动周期，采样频率设为30 Hz(可调),采样点数不低于600点。

2 舞动轨迹还原算法设计

DCM算法是MEMS惯性传感器姿态解算的常用算法。但由于受到外部机械振动和电磁环境影响，MEMS陀螺输出数据漂移较大，导致陀螺积分解算得出的姿态角误差会随着时间累积增长[9]。需要采用一种基于陀螺和加速度计的互补滤波算法实现消除累积误差，算法的框图如图2所示。

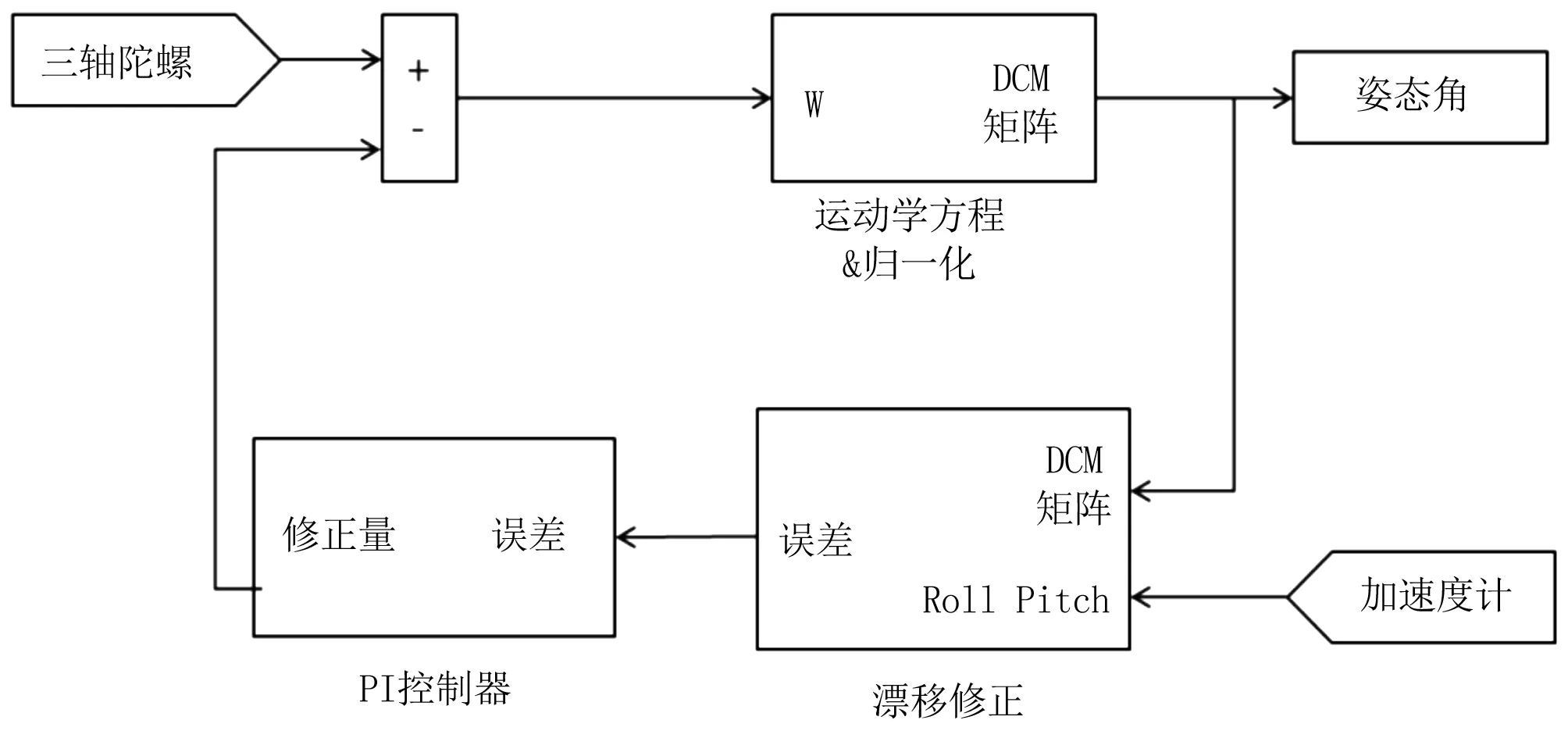
图2 互补滤波算法示意图

监测仪选用的MEMS IMU为MPU6050模块，MPU6050模块内置微处理器，可以调用DMP算法库，直接输出稳定的姿态角，因而姿态解算这一部分无需再进行算法设计，也减小了主处理器的运算量，主处理器的主要工作就是将从MPU6050获取的姿态角计算出姿态转移矩阵，然后计算出地理坐标系下的监测仪沿各轴的线加速度，再对线加速度进行积分后得到速度和位移。开始运算时设已知初始姿态角(一般由物体静止时家速度计的输出计算初始姿态角，航向角起始值设为0)，陀螺通过积分运算可以得到三维姿态角，通过下式可以将姿态角转换为方向余弦矩阵：

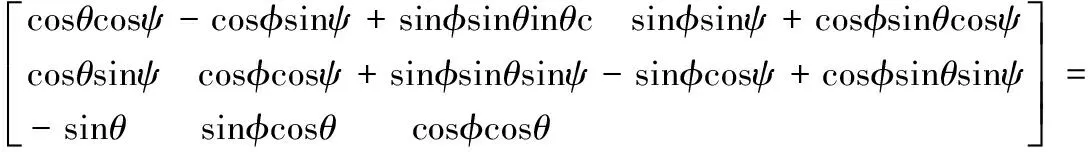
(1)

式中，θ,φ,ψ分别为载体初始的俯仰、滚转和航向角。

(2)

加速度计输出值测量的除了重力加速度g在机体坐标系中的分量以外，还包括运动加速度an沿各轴的分量，由于无法准确测量该运动加速度，所以假定加计测得的比力就是重力加速度，因此，加计测得的重力分量即为加计的输出：

(3)

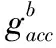
向量间的误差，可以用向量叉积来表示，ωerror就是两个重力向量的叉积，也就是误差量：

(4)

这个叉积向量是位于机体坐标系上的，而陀螺积分误差也是在机体坐标系，而且叉积的大小与陀螺积分误差成正比，恰好反馈修正陀螺，调控方法采用PI控制：

(5)

算出的修正量对陀螺的原始输出进行反馈校正：

(6)

如此，就可以提高陀螺角速度积分计算姿态角的精度。综上，惯导姿态、速度和位置更新的详细算法框图如图3所示。

图3 惯导姿态、速度和位置更新算法框图

算法的每次姿态更新流程如下：

1)IMU标定与误差补偿。

IMU在使用前必须对其进行标定校准实验，补偿各种误差以提高检测精度。惯性传感器的标定通常是在三轴转台上来完成的。高精度三轴转台价格昂贵、体积笨重，只限于实验室使用，普通用户和一般的实验室很少具备这类精密昂贵的专用实验设备，很少有条件对此类传感器做精确标定，因此三轴加速度计通常利用普通气泡水平仪、六面体盒状物实现加速度计的六位置现场简易标定。

MEMS加计误差主要有: 常值漂移误差、标度因数误差、安装误差及随机噪声等。安装误差在长时间范围内不会产生较大的变化，并且一般出厂时会通过提高安装工艺及制造工艺来减小此类误差的影响，故可以建立如下误差模型：

(7)

其中Dx，Dy，Dz是真实值，Mx，My，Mz是传感器测量值，Sx，Sy，Sz是比例因子，Bx，By，Bz是传感器的零偏。

加速度计的标定通常是在重力场下采用基于重力的多位置翻滚标定法，本文采用6位置标定传感器的输出。加速度计零位偏差校准需要在静态下进行，将传感器模块安放在一个长方体盒状物的某个面上，并使传感器的3个敏感轴方向与长方体的长宽高平行，将盒状物按位置放置在经过气泡水平仪检验后的相对水平的一个桌面上保持静止状态至2～3min，记录经过均值滤波的x轴输出记为X+1g，然后按位置2放置得到X-1g，则X轴的零位偏差Bx由式下计算出来：

(8)

同理可得其它各轴的零偏。X轴的比例因子可由下式得到：

(9)

同理可得其它各轴的零偏。MEMS陀螺仪在实验室下一般以静态时输出的均值作为陀螺的零偏。解算得到的各误差系数对IMU的原始输出进行误差补偿后可以得到更为精确的测量数据进行后续惯导系统解算。在进行加速度的惯导的速度和位置解算之前，需对INS系统进行姿态解算，确定载体在当地地理坐标系中的姿态角度，从而在当地地理坐标系中进行载体速度和位置的计算。

2)调整初始对准。

初始对准的目的是确定惯导初始状态，由于惯导系统的初始位置和速度一般准确已知，所以初始对准主要是确定惯导的初始姿态或者说是初始姿态矩阵。MEMSINS静基座下的初始对准一般采用解析式粗对准。已知处于静止状态下的加计将会敏感到重力加速度，在当地地理坐标系的投影是：

(10)

静基座下载体处于静止状态，设地速为0，则由比力方程可得：

(12)

根据gb和bn的关系可得：

(13)

(14)

故而可以计算出初始的俯仰角和滚转角，MEMSIMU由于精度比较低，无法敏感到地球自转角速度，因而无法计算出初始的航向角，可以假设初始位置时的航向角为0，在此基础上对航向角进行更新。

3)姿态更新。

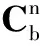
每次计算之后按下式进行坐标更新：

(15)

式中ωx,ωy,ωz为陀螺仪输出的角速度。四元数时间更新的一阶近似算法为：

(16)

其中Δθ=[ωx,ωy,ωz]·Δt，为角增量，Δt为采样时间间隔。通过以上时间更新可以得到任意时刻的姿态四元素q。

4)速度和位置更新。

当地地理坐标系下，捷联惯导的速度微分方程为：

(17)

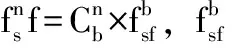
5)计算舞动频率和幅值。

通过记录一段时间内滚转角出现极大值和极小值的时刻，两个时刻的差值可以认为是导线舞动周期，从而可以计算出舞动频率。在滚转角达到极大值(极小值)时，该点处监测仪的瞬时速度为0，因而速度和位移积分的起始点可以选择从该点开始，结束于对应的滚转角极小值(极大值)处，该段时间之内计算出的位移就是这个周期内导线在该监测仪处的舞动幅值。

3 仿真与实验

为验证算法的正确性和准确性，设计了简易的舞动周期震荡模拟运动实验装置。舞动监测仪电路以2.0～5.0V的高能锂亚电池为供电电源，通过3轴惯性传感器进行加速度和角速度的采样，并将读取的模拟量经过16位AD转换，再通过SPI总线传输给IRIS模块。利用惯导装置采集原始加速度和姿态角数据数据。舞动监测仪解算后输出的位移幅值曲线如图5所示。根据本文提出的算法计算出来的东北天向位移曲线惯导装置设置为输出加速度、四元数和姿态角，通过对某个姿态角(roll或者pitch)的变化找出角度极值点的位置，从而在该位置对速度和位移清零，即在两个极值点之间进行速度和位移的积分运算。测试得到与导线走向相垂直的截面上，分别采用含有互补滤波算法和无互补滤波算法，得到舞动质点的位移对比图如图4所示。

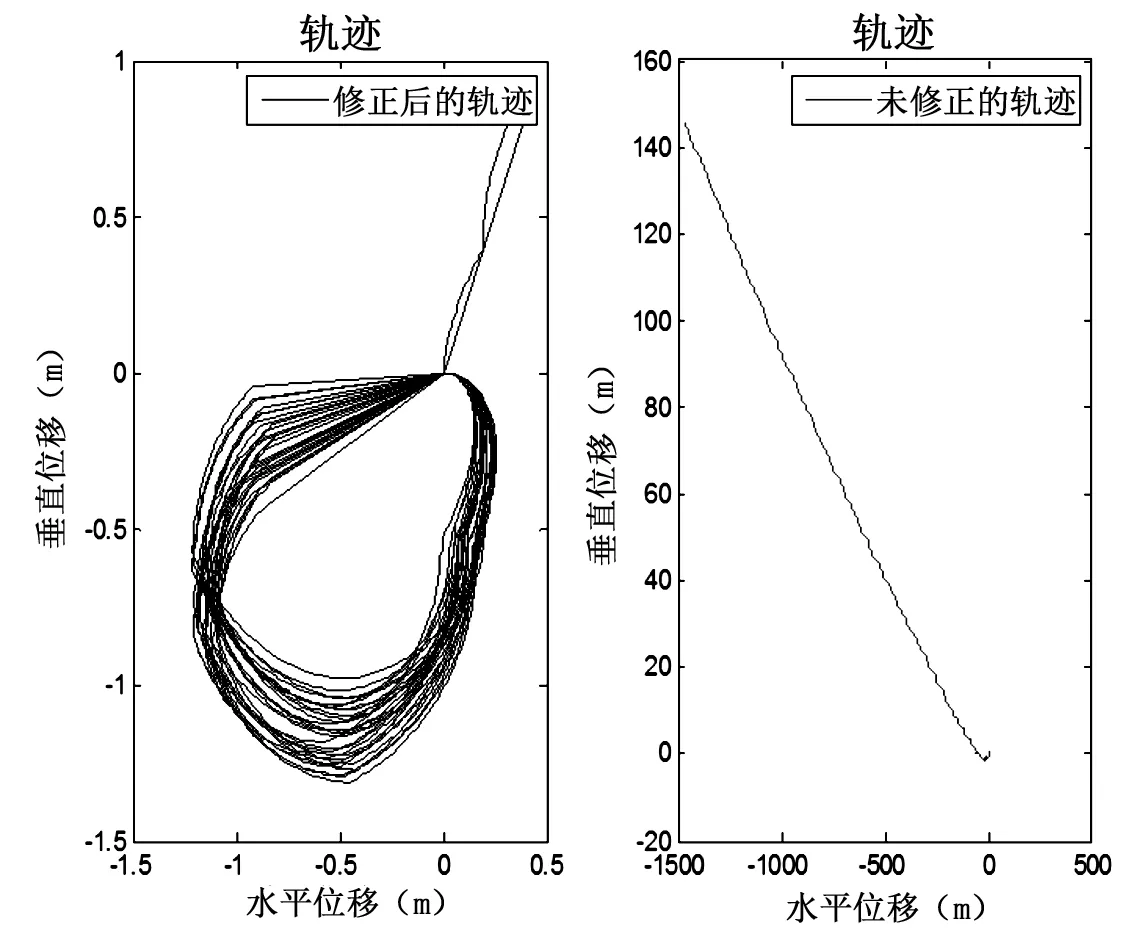
图4 滤波前后导线舞动位移数值对比图

舞动轨迹监测仪输出的结果显示，经过互补滤波算法的处理，质点的姿态角得到实时的校正，能够输出准确的舞动轨迹。而未经校正的数据几乎无法还原导线舞动的圆周轨迹。因为加速度计测量的倾角是低频信号，要滤掉高频信号，而陀螺仪要滤掉低频信号，互补滤波器就是根据传感器特性不同，通过不同的滤波器(高通或低通，互补的)，然后再相加得到整个频带的信号。加速度计测倾角的动态响应较慢，在高频信道中信号不可用，所以可通过低通抑制高频；陀螺响应快，积分后可测倾角，但是由于零漂等，在低频段信号不好。通过高通滤波可抑制低频噪声。将两者结合，就将陀螺和加表的优点融合起来，得到在高频和低频都较好的信号。经过滤波的加速度和角速度信号再参与姿态计算中，得到稳定可靠的姿态角度数据。

为了进一步验证舞动监测仪的有效性，电力科学研究院设计了专门的模拟舞动实验台，如图5所示。试验台可以固定悬挂多个监测仪，悬挂点距离圆心的距离精确可以控，旋转过程中电机可以带动滑杆调节舞动半径变化，可调半径的变化范围为0～2m。

图5 模拟舞动试验台及监测仪

根据现场多个监测点计录，统计数据得出的平均振动台振动频率 1Hz与设定的转速一致，舞动采集单元的最大幅值误差为5cm。统计数据如表1所示。

4 结论

本文基于互补滤波原理设计导线舞动轨迹还原算法，并且开发出一种新型的导线舞动监测仪。详细给出导线舞动状态监测装置的硬件设计方案和导线舞动监测仪工作流程。经过仿真测试验证，根据互补算法处理后的加计的输出计算出物体在重力场中的倾角，消除了累积误差，尤其当物体加速运动不是很显著的情况下精度较高，可以用来对姿态角度进行有效地纠正。所以这两个传感器正好可以弥补相互的缺点。最后搭建了模拟导线舞动的特殊实验测试平台，对舞动监测方案可行性和仪器的数据准确性进行了测试。在垂直方向的精度已非常接近运动直径舞动采集单元输出的幅值对于一米级别的导线舞动，其最大幅度误差绝对值不超过5cm。该舞动监测装置及新型算法能够完成舞动的三维轨迹的监测，输出数据精度达到国内电力企业标准所规定的架空输电线路在线监测要求。

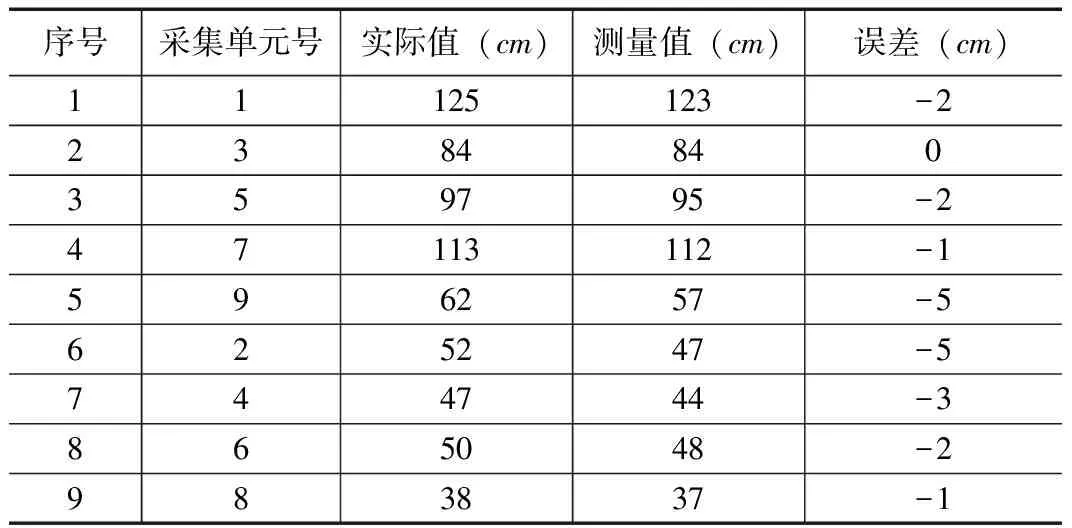
表1 模拟测试现场小幅舞动数据统计表

[1]JonesKF.CoupledVerticalandHorizontalGalloping[A].JSMEannualmeeting[C].TheJapanSocietyofMechanicalEngineers, 2006:83-84.

[2]AlonsoG,MeseguerJ,Pérez-GrandeI.Gallopinginstabilitiesoftwo-dimensionaltriangularcross-sectionbodies[J].ExperimentsinFluids, 2005, 38(6):789-795.

[3]WangJ,LilienJL.Overheadelectricaltransmissionlinegalloping.Afullmulti-span3-DOFmodel,someapplicationsanddesignrecommendations[J].PowerDeliveryIEEETransactionson, 1998, 13(3):909-916.

[4]JiangY,ZhangP,ZhangY,etal.EmbeddedPCon-lineinspectionsystemonNCequipments[J].SciencepaperOnline, 2009. (08) 577-581.

[5]胡士峰, 马建仓, 孟凡路. 基于MEMS传感器的微惯性导航系统研究[J]. 计算机测量与控制, 2009, 17(5):1015-1018.

[6]滕志军, 李国强, 何 鑫,等. 基于ZigBee的高压电气设备温度在线监测系统[J]. 电测与仪表, 2014(1):85-88.

[7]迟冬南, 徐丽娜, 栗晓云. 基于逻辑回归的匹配滤波器设计方法[J]. 计算机测量与控制, 2016, 24(3):159-162.

An Aalgorithm Based on Complementary Filtering to Reshape Galloping Track of Tansmission Line

Wang Tao1，Wu Dezhi1, Hu Ke1, Kong Hailin1, Li Rui2

(1.Zhejiang Province Electricity Company of SGCC,Wenzhou 325000, China; 2.Beijing Guowang Fuda Science and Technology Development Co., Ltd.. Beijing 100070, China)

Direction cosine matrix algorithm (DCM) is common algorithm used in industrial grade MEMS movement sensors. However, due to external mechanical vibration and strong electromagnetic environment, MEMS gyro drift output data is large, by which attitude errors of gyro integral solver appears cumulative growth from time to time. So the combination of DCM algorithm with GPS or gyro magnetic is widely adopted to calculate the angle error correction. However, this kind of monitors within the GPS and magnetic sensors appear disabled， when mounted directly on the surface of high-voltage transmission lines for existing strong power frequency electromagnetic interference environment. In order to real-time output accurate value of wire trajectory, the improved DCM algorithm is proposed that complementary filter algorithm applied to MEMS gyroscopes and accelerometers; and then a detailed galloping track solver process is designed; Finally, the validity of the new galloping monitor is proved on specified galloping experiment platform.

conductor galloping; complementary filter; accelerometer; gyroscope

2016-07-29；

2016-08-31。

国家电网公司科技项目(项目编号5211WZ140166)。

汪 滔(1977-)，男，浙江温州人，硕士研究生，高级工程师，主要从事电网运行于检修技术的研究。

李 睿(1983-)男，黑龙江鸡西人，博士研究生，主要从事在线监测技术和电力机器人研究。

1671-4598(2017)01-0173-04

10.16526/j.cnki.11-4762/tp.2017.01.049

TP212.9

A