基于伪谱法的多导弹协同攻击研究

马 骏,马清华,王 根,施文婧

(中国兵器工业第二〇三研究所，西安 710065)

基于伪谱法的多导弹协同攻击研究

马 骏,马清华,王 根,施文婧

(中国兵器工业第二〇三研究所，西安 710065)

多导弹协同攻击是未来导弹技术发展的重要方向之一;研究了多导弹协同攻击问题;首先建立了导弹与目标的相对运动方程，然后对多导弹协同攻击问题以及hp-自适应伪谱法求解最优控制问题的基本原理进行了描述；将hp-自适应伪谱法应用到多导弹协同攻击的研究中，设计了一种基于伪谱法的多导弹协同攻击制导策略，并通过仿真算例对其进行了验证和分析;仿真结果表明：设计的多导弹协同攻击制导策略能够同时兼顾时间约束和角度约束，实现对固定目标的多导弹协同饱和攻击，具有一定的应用价值。

导弹;协同攻击;伪谱方法;制导

0 引言

随着现代反导技术的不断发展，传统的单一导弹突防攻击的作战模式面临严峻的挑战，其作战效能不断减小。近年来，多导弹协同攻击的概念逐渐引起了世界各主要军事强国的关注。多枚导弹共享战场信息(目标信息、环境信息等)，协同实现作战任务，对敌方反导系统造成更大的压力，极大地提高了导弹群体的综合作战效能。多导弹协同攻击在编队突防、饱和攻击和侦察打击一体化等方面都具有广泛的应用前景，是未来导弹技术发展的重要方向之一。

目前国内外关于多导弹协同攻击的研究主要集中在具有时间约束或者具有攻击角度约束的多导弹协同攻击制导律方面，以及多导弹协同攻击时的编队队形控制问题方面。文献[1]中在有向通信拓扑下研究了导弹编队的鲁棒自适应协同跟踪控制问题。张奇在文献[2]中采用。“协同规划+相对导航”的方式来实现编队飞行，研究了编队队形保持和编队机动过程中的飞行控制方法。文献[3]中将自适应滑膜控制理论应用到导弹协同攻击编队队形控制问题的研究中。王芳等人在文献[4]中研究了“领弹-从弹”形式编队的编队协同攻击时间最优控制算法。文献[5]针对导弹编队的轨迹优化问题，提出了基于快速搜索随机树+高斯伪谱法的两阶快速轨迹优化方法。赵世钰和周锐在文献[1]中提出了一种双层协同制导结构，基于该协同制导结构并针对多导弹同时击中目标这一特定协同任务,给出了一种具体可行的多导弹协同制导律。文献[2]针对多导弹时间协同攻击目标问题,提出了一种领弹-被领弹策略。领弹向被领弹传递其状态参数，被领弹接受领弹的控制,使各枚被领弹都按照领弹的攻击时间同时攻击目标,从而实现多导弹时间协同导引。韦常柱等在文献[3]中对导弹协同作战编队的飞行控制系统进行了研究提出了具有3个回路的导弹协同作战编队飞行控制系统。邹丽等在文献[4]中针对多导弹编队齐射攻击在时间上的协同要求，将攻击时间可控制导律与一致性分散化协调算法相结合，提出了一种多导弹编队齐射攻击的分散化协同制导方法。文献[5]中对多导弹协同制导策略进行了研究;文献[6]中设计了基于局部模型预测控制的主动防碰撞导弹编队队形保持控制器，应用在编队队形的变换控制策略中。文献[7-8]对多导弹协同编队的队形保持控制问题进行了研究。Lee Jin-Ik等人设计了一种新的寻的制导律实现了多枚导弹以指定时间和角度的协同控制[9]。在文献[10]中Jung Bok-Yung等人研究了同时考虑角度控制和时间控制的三维控制律形式,并进行了数值仿真验证。

本文将伪谱方法应用到多导弹协同攻击的研究中，设计同时兼顾时间约束和角度约束的多导弹协同攻击制导策略，具有一定的应用价值。首先建立了二维平面内导弹和目标的相对运动方程；然后详细描述了多导弹协同攻击问题；其次介绍了hp-自适应维普算法的基本原理，并设计了一种基于伪谱方法的多导弹协同攻击制导策略；进而通过仿真算例对设计的多导弹协同攻击制导策略进行了验证和分析；最后给出了本文的结论。

1 弹目相对运动方程

为简化分析过程，本文只考虑二维平面内导弹与目标的几何运动关系，据有一定的通用性。首先作如下假设条件：

1)导弹和目标视为二维平面内的质点，忽略具体外形及周围复杂环境的干扰；

2)各导弹的速度(用V表示)大小相同且保持不变；

3)控制量为导弹的法向加速度(用ai表示)，其只改变导弹飞行速度的方向，不改变导弹飞行速度的大小；

4)目标为静止目标。

在二维坐标系Oxy内，Mi为第i枚导弹，T为静止目标，ri为第i枚导弹的弹目距离；σi为第i枚导弹的速度矢量与基准线(Ox轴)的夹角，即导弹弹道角，从基准线逆时针转到导弹速度矢量时σi为正；ηi为第i枚导弹的速度矢量与目标线的夹角，即导弹前置角，从速度矢量逆时针转到目标线上时ηi为正；qi为第i枚导弹的目标线与基准线的夹角，即目标线角，若从基准线逆时针转到目标线上时qi为正。根据图1所示的导弹与目标的几何运动关系,可以获得第i枚导弹与目标的相对运动方程组为：

图1 弹目相对运动方程

(1)

考虑qi=σi+ηi，则有：

(2)

取状态变量为：

(3)

取控制量为：

(4)

则式(1)可以表示为：

(5)

2 多导弹协同攻击问题

与单一导弹攻击模式不同，多导弹协同攻击能够实现在特定时刻对目标的多角度饱和攻击，增加敌方导弹防御系统的拦截难度，提高我方的导弹群的作战效能。为了分析本文研究的多导弹协同攻击问题，首先做出以下假设：

1)导弹MA、MB和MC的发射位置不同(如图2所示)；

2)导弹MA、MB和MC完全相同(发射后各具有相同的飞行速度，且各导弹法向加速度的变化范围相同)；

3)各枚导弹同时发射，且要求各导弹在同一时刻以不同的角度命中目标，从而实现对目标的饱和攻击。

图2 多导弹协同攻击任务示意图

显然，三枚导弹的发射位置不同，与目标的距离也不同。MA距离目标最远，MC距离目标最近。由于各导弹具有相同的飞行速度，且作为控制量的法向加速度变化范围均相同，因此为了实现同时刻发射并在同一时刻以不同方向命中目标，必须合理设计各枚导弹的飞行弹道，并控制各导弹沿着设计的弹道飞行，最终在同一时刻以不同的弹道角命中目标。

另外，公式(5)表示的模型中，导弹的法向加速度是唯一的控制量。一般情况下，希望导弹攻击目标的过程中导弹法向过载的变化较小。最优控制是现代控制理论的一个重要组成部分。其所研究的问题是：对一个控制系统，在给定的性能指标要求下，如何选择控制规律，使性能指标达到最优(极值)[11]。hp-自适应伪谱算法求解最优控制问题时具有精度高，收敛速度快的特点[12-15]。求解最优控制问题时hp-自适应伪谱算法的目标函数既包括了控制量约束也包括了时间约束。

本文使用hp-自适应伪谱算法求解具有时间和角度约束的导弹协同攻击问题。首先选择距离目标最远的导弹(MA)作为基准，通过hp-自适应伪谱算法设计其飞行弹和命中目标的时刻；然后求解其它与目标距离相对较近的导弹的飞行弹道和命中时刻(与MA命中时刻相同)，进而实现多导弹对目标的协同攻击。

3 hp-自适应伪谱法基本原理

文献[15]中对hp-自适应伪谱算法基本原理进行了详细描述。hp-自适应伪谱算法首先将时域区间分为若干段，并在每段上选取一定数量的Legendre-Gauss点作为配点，然后在每个单元上利用Lagrange多项式逼近系统的状态变量和控制变量，并通过插值函数的微分和被积函数的高斯积分来近似系统的状态微分和性能指标，从而将连续的最优控制问题转化为离散的非线性规划问题，最后通过使用自适应的配点调整策略和相关的规划求解算法求解离散后的非线性规划问题，从而实现对于最优控制问题的求解。

4 仿真算例与分析

目标函数的选取以导弹的控制指令消耗最小为原则，即：

(6)

动力学约束为式(5)，路径约束取为：

(6)

终端约束由表1中的仿真参数确定，即导弹与目标的相对位置不同、发射角度不同，要求求解各导弹的飞行弹道，使各枚导弹在同一时刻以不同的导弹弹道角命中目标，从而实现对目标的多角度协同饱和攻击。

在以上目标函数和约束条件下，首先利用hp-自适应伪谱法求解距离目标最远的导弹MA的飞行弹道和命中目标所需要的飞行时间。显然，导弹MA的位置与要求的命中目标时的导弹弹道角决定了导弹MA的飞行弹道为一条直线，且其作为控制量的法向加速度为零值。另外，导弹MA命中目标所需时间为tf=40s。在此基础上，继续求解导弹MB和导弹MC在终端约束条件下，且命中时间为tf=40s条件下的飞行弹道和法向加速度。仿真结果如图3～7所示。

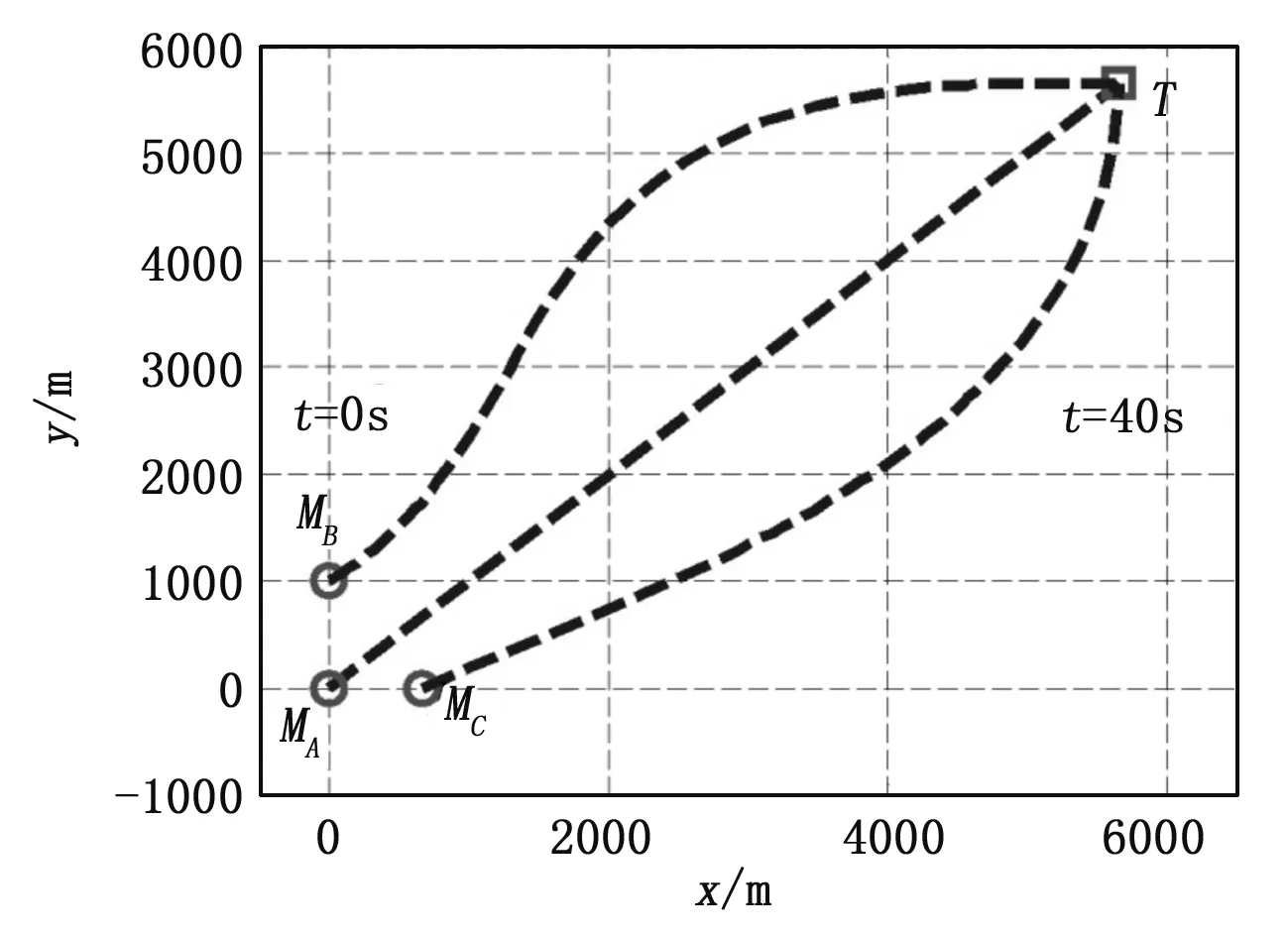
图3 导弹飞行弹道

图4 导弹MA状态

图5 导弹MB状态

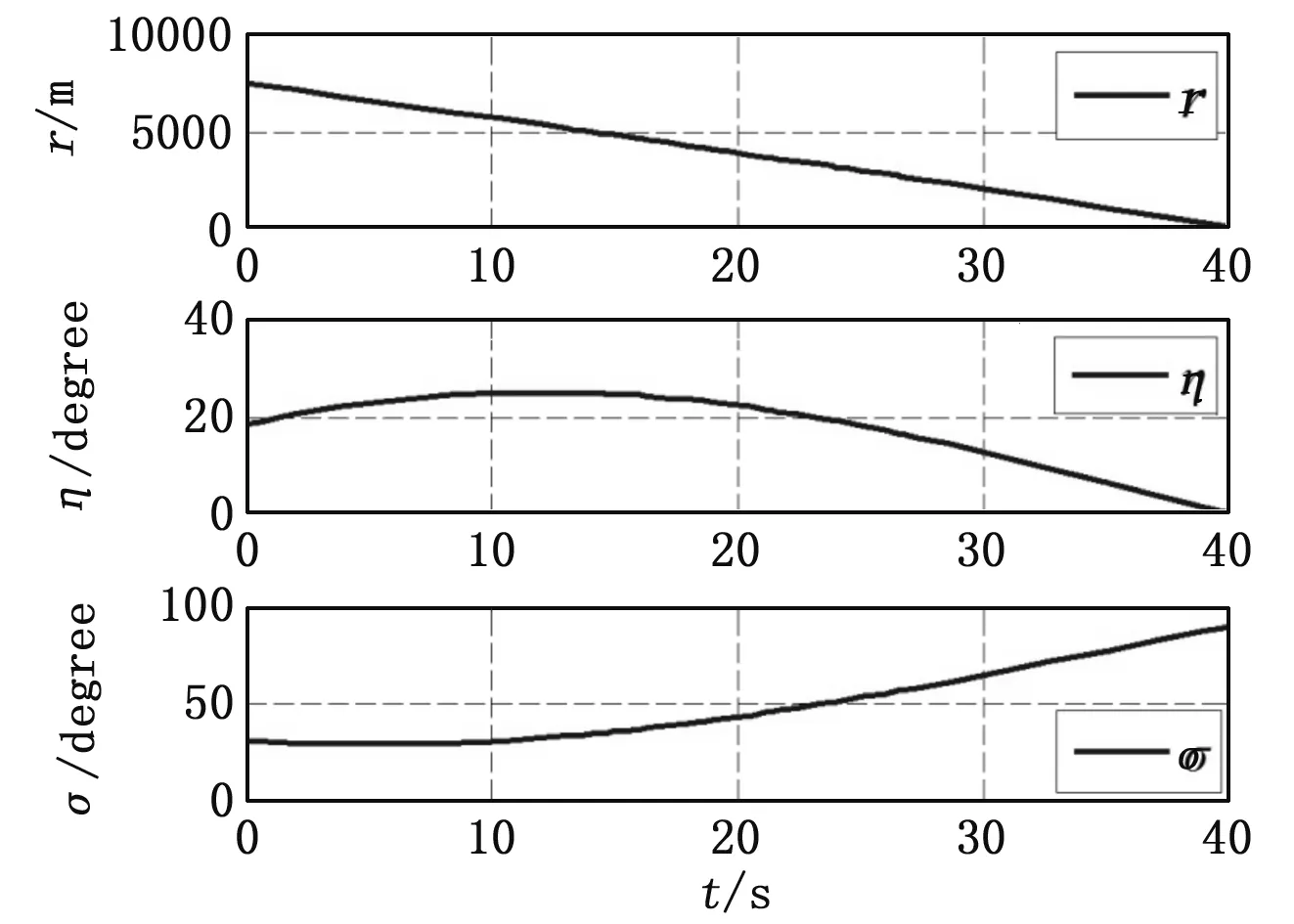
图6 导弹MC状态

图7 导弹法向加速度比较

图3为求解的导弹MA、导弹MB和导弹MC的飞行弹道，图4、图5和图6分别为导弹MA、导弹MB和导弹MC的弹目距离、导弹前置角和导弹弹道角随时间的变化情况，图7为导弹MA、导弹MB和导弹MC飞行过程中法向加速度随时间的变化情况。图中仿真结果表明：

1)各枚导弹以不同的发射位置和导弹弹道角发射，最终在40s时以不同的弹道角(σA=45°,σB=0°,σC=90°)命中目标，满足终端约束条件的要求；

2)从图3中可以看到，导弹MA的飞行弹道为直线状态，而导弹MB和导弹MC的飞行弹道则比较弯曲。从物理意义上来说，导弹MA距离目标最远，要求的tf=40s以及初始发射角度决定了其必须以直线弹道攻击目标；而导弹MB和导弹MC距离目标较近，为了与导弹MA同时命中目标，其弹道必然变得比较弯曲，以等待最远的导弹MA；

3)从图7中可以看到，导弹MA飞行过程中作为控制量的法向加速度保持为零值，这是由于导弹MA的飞行弹道为直线弹道，飞行过程中不需要调整弹道轨迹；而导弹MB和导弹MC需要用法向加速度的变化获得较为弯曲的飞行弹道，进而实现与导弹MA同时命中目标的目的。

图8 导弹飞行弹道

图9 导弹法向加速度比较

另外，hp-自适应伪谱法也可以时间消耗作为目标函数，即以命中目标所需时间最短为指标。图8为发射位置位于坐标原点的导弹分别以不同的导弹前置角攻击位于(5 656.9,5 656.9)的目标的飞行弹道。导弹的初始目标线角为45，命中目标时的导弹弹道角均为90°。从图中曲线可以看到，导弹的前置角越小，则命中目标所需时间也越短。图9为对应导弹前置角条件下导弹飞行过程中法向加速度的变化情况。以公式(23)作为性能指标，则有η0=5°时J=1 043.9，η0=22.5°时J=858.3，η0=45°时J=1 108.0。可见，导弹前置角为22.5°时其控制量消耗最少，导弹前置角过大或者过小时都必须消耗更多的控制量来满足弹道角终端约束条件(命中目标时导弹弹道角为90°)。

5 结论

多导弹协同攻击是未来导弹技术发展的重要方向。本文针对多导弹协同攻击问题进行了研究。首先建立了导弹和目标的相对运动方程，然后利用hp-自适应伪谱算法设计了一种同时兼顾时间约束和角度约束的多导弹协同攻击制导策略，并通过仿真算例进行了验证和分析。仿真结果表明：设计的基于伪谱法的多导弹协同攻击制导策略能够有效地实现多导弹对固定目标的饱和攻击。另外，仿真中还发现，导弹的飞行弹道由弹目相对位置、发射角度、命中角度决定。

[1] 周慧波，宋申民，郑 重. 导弹编队协同攻击分布式鲁棒自适应控制[J].中国惯性技术学报,2015,23(4):516-521.

[2] 张 奇.多弹编队飞行控制技术研究[J].导弹定位与授时,2014,1(2):30-34.

[3] 张 磊，方洋旺，毛东辉,等. 导弹协同攻击编队自适应滑模控制器设计[J].宇航学报，2014,35(6):700-707.

[4] 王 芳，林 涛，张 克,等.多阶段高斯伪谱法在编队最优控制中的应用[J].宇航学报，2015: 36(11):1262-1269.

[5] 黄 荣，崔乃刚，韦常柱,等. 基于RRT-GPM两阶策略的导弹编队协同突防最优轨迹快速设计[J]. 中国惯性技术学报，2015,23(3): 356-362.

[6] 赵世钰,周 锐.基于协调变量的多导弹协同制导[J].航空学报，2008,29(6):1605-1611.

[7] 张友安,马国欣,王兴平. 多导弹时间协同制导:一种领弹-被领弹策略[J]. 航空学报，2009, 30(6):1109-1118.

[8] 韦常柱,郭继峰,赵 彪.导弹协同作战编队飞行控制系统研究[J].系统工程与电子技术，2010,32(9):1968-1972.

[9] 邹 丽，周 锐，赵世钰，等.多导弹编队齐射攻击分散化协同制导方法[J].航空学报，2011,32(2):281-290.

[10] 吴胜亮.众多导弹协同作战制导控制的研究[D].南京：南京航空航天大学, 2013.

[11] 杜 阳,吴森堂.飞航导弹编队队形变换控制器设计[J].北京航空航天大学学报, 2014, 40(2):240-245.

[12] 马培蓓,张友安,于 飞,等.多导弹编队保持控制器设计[J].飞行力学,2010,28(3):69-73.

[13] 马培蓓,纪 军. 多导弹三维编队控制[J]. 航空学报，2010,31(8):1661-1666.

[14]LeeJI,JeonIS,TankMJ.Guidancelawusingaugmentedtrajectory-reshapingcommandforsalvoattackofmultiplemissiles[J].ProceedingsoftheICC,2006.

[15] 黄攀峰,张 帆,刘彬彬,等.辐射开环空间绳系机器人编队自旋转速最优控制[J].系统工程与电子技术.2015, 37(6):1362-1369.

[16]JungBY,KimYD.Guidancelawsforanti-Shipmissilesusingimpactangleandimpacttime[Z].Colorado:AmericanInstituteofAeronauticsandAstronautics,2006:1-13.

[17] 周凤岐,强文鑫,阙志宏. 现代控制理论引论[M]. 北京：国防工业出版社，1988.

[18] 胡仄虹,黄攀峰,孟中杰,等. 空间绳系机器人逼近过程的位姿一体化控制[J]. 航空学报. 2013,34(11):2635-2644.

[19]BensonDA,HuntingtonG.T,ThorvaldsenTP,etal.Directtrajectoryoptimizationandcostateestimationviaanorthogonalcollocationmethod[J].JournalofGuidance,Control,andDynamics, 2006,29(6):1435-1440.

[20]GargD,HagerWW,RaoAV.Pseudospetralmethodsforsolvinginfinite-horizonoptimalcontrolproblems[J].Automatica,2011,47(4):829-837.

Study on Guidance for Cooperative Engagement of Multi-missile Based on Pseudo-Spectral Method

Ma Jun，Ma Qinghua, Wang Gen, Shi Wenjing

(No.203 Research Institute, China Ordnance Industries, Xi’an 710065,China)

The cooperative engagement of multi-missile is one of the significant trend of missile technology. The cooperative engagement of multi-missile is investigated in this paper. Firstly a reasonable model is used to describe the relative motion of the missile and the target. Secondly the hp-adaptive pseudo-spectral method is described. Thirdly, a guidance strategy for cooperative engagement of multi-missile based on pseudo-spectral method is proposed. Finally some digital simulations are implemented. The simulation results indicate that the proposed guidance strategy is effective in the saturated attack mission of multi-missile, and the time restriction and angle restriction are considered.

missile; cooperative engagement; pseudo-spectral method; guidance

2016-08-05；

2016-08-31。

马 骏(1985-)，男，陕西商洛人，博士，工程师，主要从事导弹制导与控制方向的研究。

1671-4598(2017)01-0094-04

10.16526/j.cnki.11-4762/tp.2017.01.027

TJ761.1

A