混沌神经动力学行为在多自由度机器人上的应用研究
2017-02-27夏东盛李永涛
夏东盛,李永涛
(1.陕西工业职业技术学院,陕西 咸阳 712000; 2.西安能合电子科技有限公司,西安 710000)
混沌神经动力学行为在多自由度机器人上的应用研究
夏东盛1,李永涛2
(1.陕西工业职业技术学院,陕西 咸阳 712000; 2.西安能合电子科技有限公司,西安 710000)
把高维的混沌神经动力学行为应用到多但有限自由度的机器人以实现适应性控制是一个困难的问题;借鉴大量神经元控制少数肌肉的生物事实,一种简单的神经编码方法被用来使高维的神经网络模式转化成了低维的运动参数;虽然只在神经网络中嵌入了3种简单的姿势动作,但是在混沌神经动力学行为出现时,机器人手臂呈现出复杂的组合运动;利用这一点,提出了一个简单的控制算法用来解决病态问题(不一定有解或者确定的解无法保证的问题);实装实验进一步表明,尽管只有粗略甚至不确定的光源信息,利用提出的控制算法,机器人手臂可以成功的寻找到光源。
混沌神经动力学; 机器人手臂 ; 病态问题; 神经编码
0 引言
大脑作为世界上最复杂的系统之一,已经吸引了大量跨学科,包括生物,化学,信息,物理,计算机,通信,医学,心理学等研究者的兴趣。尽管大量的研究成果让我们对大脑的了解越来越多,但建立在传统学科细分基础上的研究让我们只见树木不见森林,很难真正深刻理解大脑的工作机制。特别是面对大脑中巨大的神经网络所涌现出的复杂动力学行为,传统的方法往往或多或少的陷入“组合性爆炸”(combinatorial explosion)或者“程序复杂性”(program complexity)[1]。
作为系统性科学发展的新阶段,复杂性科学的兴起带动了对复杂系统所进行的横跨多学科的系统性科学研究的同时,也为解决传统方法的缺陷带来了新的思路。对于大脑的研究来说,混沌现象在生物实验中的发现[2-3]让混沌理论在脑科学研究中成为了一个热点。先锋的研究者们在探索混沌究竟在人脑中有什么作用[4-8]的时候,也在试图用混沌来实现某些功能,比如联想记忆[9-10],信息编码[11],记忆搜索[12-13]和伪记忆消除[14]等。有趣的是,日本冈山大学的末光在理论计算中把混沌引入到了自律控制当中[15],然后,李更进一步发展了这个思想,设计并实装了一个混沌神经网络控制的小车机器人,实现了迷路求解问题[16]。理论和实验结果都显示,混沌运动不同于随机运动,在适应性控制中具有特别的优势。但是迷路求解问题中,小车机器人只有两个自由度,那么在面对多自由度控制对象时,情况又会怎样呢?为了回答这个问题,本文中建立了一个控制系统,用混沌神经网络来控制一个多自由度的机器人,并且提出了一个简单的控制算法,利用简单的神经编码函数,实现了复杂的控制过程。相较于传统机器人控制算法中,机器人自由度增加所带来的极端程序复杂性,这种算法不但简单而且具有很强的适应性。
1 控制系统构架
1.1 控制系统组成
控制系统主要由神经网络仿真计算机,多自由度的机器人,和两者之间信息交换的无线通信系统以及机器人侧的传感器组成,如图1所示。神经网络仿真计算机属于核心部分,相当于人的大脑,根据机器人侧的传感器送来的数据,完成神经网络的模式更新,生成机器人各自由度的控制信息。这些信息通过蓝牙通信送给机器人,实现机器人的运动控制。

图1 控制系统示意图
1.2 多自由度机器人
本文中的机器人采用日本RT公司的机械臂(如图2),共有5个微型伺服电机控制,他们的旋转角度范围如下表1。

表1 伺服电机的旋转角度范围Servo1α1180°Servo2α2135°Servo3α3120°Servo4α4180°Servo5α590°
图2 日本RT公司5自由度机器人手臂
神经网络仿真计算机作为最核心的部分,采用Intel core i3 处理器,4 GB内存的计算机。神经网络运算采用C++编程运行在Linux操作系统中。蓝牙通信系统不是本文的重点,所以不再详述。下文将着重描述本文的核心部分——神经网络的理论基础和算法。
2 神经网络模型
本研究基于一个由N个神经元组成的非对称递归神经网络模型(Recurrent Neural Network Model),如图3所示。
每个神经元的激活函数为:
(1)

(2)
第i个神经元xi接受第j个神经元xj的输入连接权值用Wij来表示。由于每个神经元与除自己以外的其他神经元相连,所以Wij=0。参数r表示与每个神经元相连的神经元数目,称为连接数。配置函数Gi(r)表示输出连接到第i个神经元的神经元序号的集合。神经元的激活函数采用阈值函数,θi表示第i个神经元的阈值,为简单起见,取θi=0。每个神经元有两个状态:激活或者非激活状态分别用1和-1表示。因此,神经网络的状态模式可以用一个N维的状态向量X表示。如果用实心方块“■”表示激活状态,空心方块“□”表示非激活状态,则N维的状态向量X可以表示成图形模式,如图3所示。
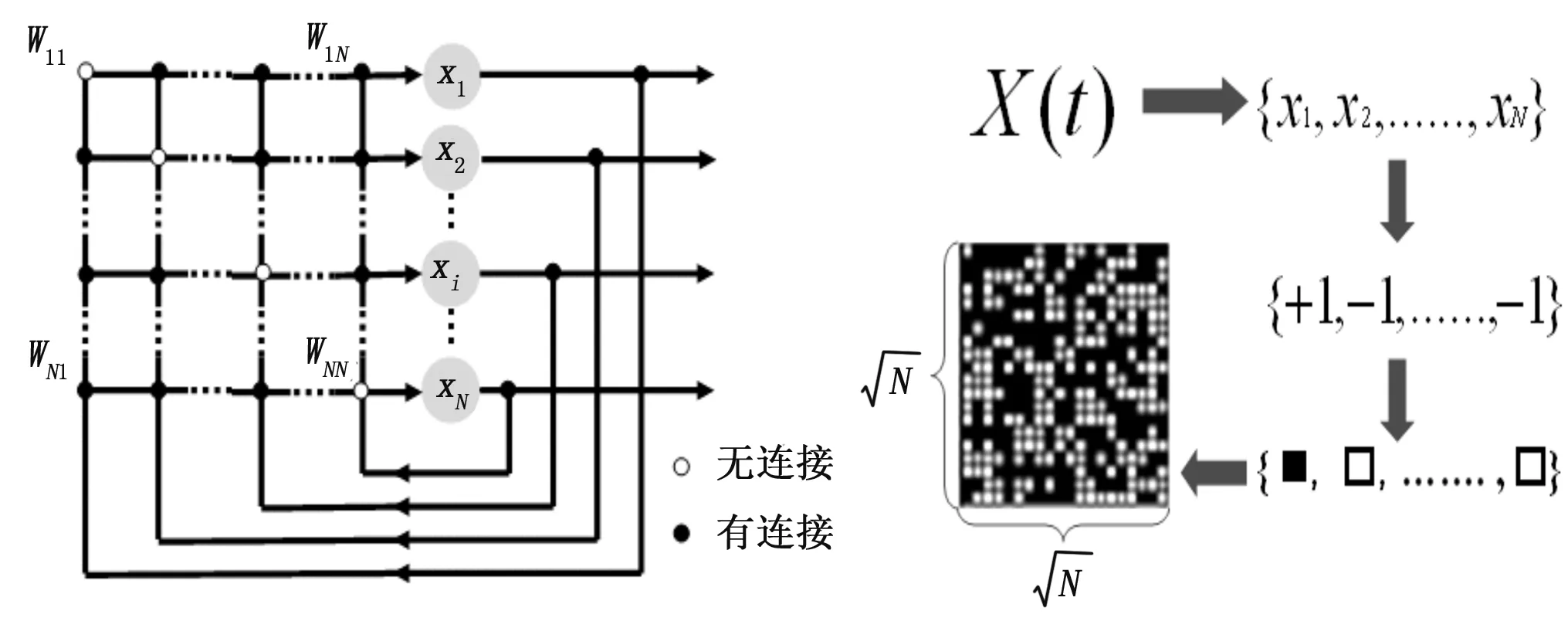
图3 非对称递归神经网络模型
从神经元的激活函数可以看出,影响神经网络状态变化的关键参数是连接数r和连接权值矩阵W={Wij}。首先,在取r=N-1的状况下, 通过一种正交化学习法[17],可以确定一个非对称的连接权矩阵W={Wij},并把极限环吸引子模式学习进神经网络中。假设有M个N维神经网络模式,被分为L组,每组包含K个,即M=K×L,那么这些神经网络模式可以用符号表示成{ξμ,λ|μ = 1,2,…,L;λ = 1,2,…,K}。如果取ξμ,λ + 1= ξμ,1,通过式(3)的正交化学习学习,确定的连接权值矩阵W使M个N维神经网络模式成为L个包含K个模式的极限环吸引子。
(3)
一旦连接权值矩阵W已经确定,对于任意的初始神经网络模式,如果r=N-1,神经网络的状态在有限次的更新之后K倍数周期性地出现L组中的其中一组。因此,L组模式实际上是L个极限环吸引子。然而随着连接数r逐渐变小,极限环吸引子逐渐变的不稳定,最终当r足够小(r< 图4 N维相空间状态迁移示意图 科学研究表明,人的大脑中神经元的数目大约为1011个[20],但是人的肌肉数只有区区几百块。这从一个侧面反映了神经控制肌肉时具有极大的冗余度的同时,也意味着具备极高灵活性和适应性的行为与大量神经元所表现的复杂动力学行为相关。假设控制对象具有(个自由度(m< 图5 N维神经网络模式编码成Γ个自由度运动函数 本文中神经网络的神经元数目N=400,控制对象机器人手臂的自由度Γ=5,所以采用分割向量的方法进行神经网络模式编码(如图6)。 图6 分割向量的方法进行神经网络模式编码 (4) (5) (6) (7) 为了验证混沌神经网络状态在多自由度机器人自适应性控制中的有用性,本文设计了一个寻找光源实验。在离机器人手臂50cm的地方安装了一个灯泡作为点光源,机器人手臂利用其指端安装的光敏传感器来寻找这个点光源,最终机器人手臂伸直接近光源表示实验成功,如图7所示。 图7 寻找光源实验 在该实验中,因为有3个具有指向性的光敏传感器,所以通过比较信号强度的方法,判断光源的大概位置实在正面,左面还是右面。光敏传感器的指向性测试结果如图8所示。如果光敏传感器检测到光源在机械臂指端的正前方(光敏传感器左右45°之间)时,把这些信息通过蓝牙传给神经网络仿真计算机,神经网络模式以r=N-1更新,否则以r< 图8 光传感器设计安装及指向性测试 图9 控制算法 首先,神经网络仿真计算机根据机器人手臂侧的传感器信息判断灯是否在手臂的正前方范围内。如果“是”,神经网络以足够大的连接数进行一步更新,对应产生典型规则运动的片段,否则,神经网络以足够小的连接数进行一步更新,对应产生复杂的组合运动。神经计算的结果经过神经编码形成机器人手臂的运动指令,通过蓝牙通信发送给机器人手臂。机器人手臂的相应伺服电机根据运动指令旋转运动,然后机器人手臂侧的传感器收集灯光信息,判断3个传感器中哪个方向信号最强,并上传给神经网络仿真计算机,从而开始新的更新循环。 图10 寻找光源实验过程截图 本文基于一个非对称递归神经网络模型,通过改变一个重要参数——连接数r,可以使神经网络模式在极限环吸引子和混沌迁移之间切换。根据生物神经和肌肉之间的极大冗余度,引入一个简单的神经编码运动函数,把神经网络模式转化为多自由度机械臂的运动,并通过光源寻找实验验证了混沌动力学行为在多自由度适应性控制问题中的有用性。不但为再进一步,把混沌动力学行为应用到更复杂的控制问题中奠定了基础,也表明了合理的利用混沌神经网络可以使复杂的问题得到简单解决方法。 [1]BlumC,RoliA.Metaheuristicsincombinatorialoptimization:Overviewandconceptualcomparison[J].ACMComputingSurveys(CSUR), 2003,35(3):268-308. [2]SkardaCA,FreemanWJ.Howbrainsmakechaosinordertomakesenseoftheworld[J].BrainandBehavioralScience, 1987,10: 161-195. [3]HayashiH,IshizukaS,OhtaM,etal.ChaoticbehaviorintheOnchidiumgiantneuronundersinusoidalstimulation[J].PhysicsLettersA, 1982,88(8): 435-438. [4]TsudaI.ChaoticitinerancyasadynamicalbasisofHermeneuticsinbrainandmind.WorldFutures[J]. 1991,32:167-184. [5]BabloyantzA,DestexheA.Low-dimensionalchaosinaninstanceofepilepsy[J].PNAS, 1986,83(10):3513-3517. [6]Shil’nikovA,NicolisG,NicolisC.BifurcationandPredicabilityAnalysisofAorderAtmosphericCirculationModel[J].Int.J.BifurcationChaos,1995(5):1701. [7]FujiiH,ItohH,IchinoseN,etal.Dynamicalcellassemblyhypothesis—Theoreticalpossibilityofspatio-temporalcodinginthecortex[J].NeuralNetworks, 1996(9): 1303-1350. [8]KuroiwaJ,NaraS,AiharaK.Functionalpossibilityofchaoticbehaviourinasinglechaoticneuronmodelfordynamicalsignalprocessingelements[A].In: 1999IEEEInternationalConferenceonSystems,Man,andCybernetics(SMC’99)[C]. (pp. 290-295),1999. [9]AiharaK,TakabeT,ToyodaM.Chaoticneuralnetworks.PhysicsLettersA[J]. 1990,144(6-7): 333-340. [10]IkeguchiT,AdachiM,AiharaK.ChaoticNeuralNetworksandAssociativeMemory,in“ArtificialNeuralNetworks” (ed.A.Prieto)[J].LectureNotesinComputerScience, 1991,540(17-24),Springer-Verlag,Berlin. [11]NaraS,DavisP.Chaoticwanderingandsearchinacyclememoryneuralnetwork[J].ProgressofTheoreticalPhysics, 1992,88:845-855. [12]NaraS,DavisP,KawachiM,etal.Memorysearchusingcomplexdynamicsinarecurrentneuralnetworkmodel[J].NeuralNetworks, 1993,6:963-973. [13]ParodiG,RidellaS,ZuninoR.Usingchaostogeneratekeysforassociativenoise-likecodingmemories[J].NeuralNetworks, 1993, 6(4):559-572. [14]MatsumotoG,AiharaK,HanyuY,TakahashiN,YoshizawaS,etal.Chaosandphaselockinginnormalsquidaxons[J].PhysLettA, 1987,123:162-166. [15]SuemitsuY,NaraS.Asolutionfortwo-dimensionalmazeswithuseofchaoticdynamicsinarecurrentneuralnetworkmodel[J].NeuralComputation, 2004,16 (9):1943-1957. [16]LiY,NaraS.Applicationofchaoticdynamicsinarecurrentneuralnetworktocontrol:hardwareimplementationintoanovelautonomousrovingrobot[J].BiologicalCybernetics, 2008,99:185-196. [17]NaraS,DavisP,KawachiM,etal.Chaoticmemorydynamicsinarecurrentneuralnetworkwithcyclememoriesembeddedbypseudo-inversemethod[J].InternationalJournalofBifurcationandChaosinAppliedSciencesandEngineering, 1995,5:1205-1212. [18]NaraS.Canpotentiallyusefuldynamicstosolvecomplexproblemsemergefromconstrainedchaosand/orchaoticitinerancy[J].Chaos, 2003,13(3):1110-1121. [19]LiY,NaraS.Noveltrackingfunctionofmovingtargetusingchaoticdynamicsinarecurrentneuralnetworkmodel[J].CognitiveNeurodynamics, 2008,2:39-48. [20]GazzanigaS,IvryR,MangunG,CognitiveNeuroscience:TheBiologyoftheMind[M].WWNorton&Company; 第四版 (October1, 2013). Study on Application of Chaotic Dynamic Behavior in Multi Degree of Freedom Robot Xia Dongsheng1, Li Yongtao2 (1.Information Engineering Department, Shanxi Polytechnic Institute, Xianyang 712000, China; 2.Research and Development Department, Xi’an Nenghe Electronic Science Co. Ltd., Xi’an 710000, China) It is quite difficult that chaotic neural dynamics in higher dimension is applied to robots with multiple (but finite) degree of freedom (DOF). Inspired by the fact that fewer muscles are controlled by a larger number of neurons, a simple coding method enables higher dimensional neural pattern to be translated into lower dimensional motion parameters. Although only three typical gestures are embedded into the neural network, the robot shows complex motions when chaotic neural dynamics emerges. By means of this point, a simple control algorithm was proposed to solve an ill-posed problem, which means that the existence of solution cannot be guaranteed or certain solution cannot be guaranteed. Furthermore, experiments on hardware implementation indicate that the arm robot can find light source with rough and uncertain information successfully using the algorithm. chaotic neural dynamics; arm robot; ill-posed problem; neural coding 2016-07-22; 2016-08-31。 夏东盛(1975-),男,陕西咸阳人,副教授,主要从事自动控制、多媒体技术方向的研究。 1671-4598(2017)01-0070-04 10.16526/j.cnki.11-4762/tp.2017.01.020 TM44 A
3 神经网络模式编码与运动函数


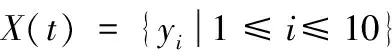
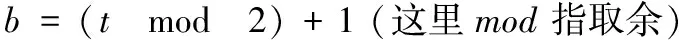
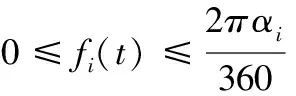
4 寻找光源实验



5 总结
