卫星时变网络中基于连接计划的最短路径优化算法
2017-02-24戴翠琴
戴翠琴,李 剑,唐 煌
(重庆邮电大学 移动通信技术重点实验室,重庆 400065)

卫星时变网络中基于连接计划的最短路径优化算法
戴翠琴,李 剑,唐 煌
(重庆邮电大学 移动通信技术重点实验室,重庆 400065)
在卫星时变拓扑网络中,针对Dijkstra最短路径算法不能时刻保证路径最优的问题,结合卫星节点运动规律的确定性,研究分析了卫星网络拓扑动态变化的周期性特征,提出了一种基于连接计划(contact plan, CP)的最短路径算法(CP-Dijkstra)。在低轨 (low earth orbit, LEO) 卫星系统中,首先根据不同时刻星间链路的时变连接情况形成动态CP,然后根据CP是否发生改变对信息进行不同的处理:当节点检查到CP未改变,则根据之前计算的最短路径进行转发;反之,则根据当前最新的CP重新计算到达目的节点的最短路径,直至信息成功转发到目的节点,从而确保信息经过的一系列路径序列为最短路径。仿真结果表明,与卫星时变网络中常用的动态虚拟拓扑路由(dynamic virtual topology routing, DVTR)算法相比,CP-Dijkstra算法不仅能够较好地提升网络吞吐量,而且可以有效地降低网络平均时延和丢包率。
卫星时变网络;最短路径算法;连接计划;吞吐量;丢包率
0 引 言
与地面通信网络相比,卫星通信网络能够实现远距离大容量的空间信息传输,但是空间节点有限的存储和处理能力,以及周期性的动态轨道运动,使得网络拓扑结构和链路权值随着卫星运行时间变化而呈现周期性变化,因此传统地面网络中的路由算法不能直接应用到卫星网络中。近年来,随着人们对空间宽带通信的需求与日俱增,具有星间链路(inter-satellite link, ISL)及星上处理能力的新一代宽带卫星通信网络中的关键技术,尤其是路由算法研究受到了人们广泛的关注[1-2]。
目前,针对卫星网络拓扑动态时变的特性,已有的研究[3-7]通常采用虚拟拓扑控制策略来屏蔽拓扑的动态性,进而针对静态的拓扑序列进行路由优化计算。虚拟拓扑控制策略:一个系统周期T被划分为若干个时间片[t0,t1],[t1,t2],[t2,t3],…,[tn-1,tn],ISL的变化仅在时间点t1,t2,…,tn发生,且假定每个时间片[ti,ti+1]内的卫星网络拓扑不变,从而将卫星网络的动态拓扑离散化为若干个静态拓扑。文献[3] 在低轨(low earth orbit, LEO) 卫星通信网络中,提出了一种基于虚拟拓扑策略的离散时间动态虚拟拓扑路由(discrete-time dynamic virtual topology routing, DT-DVTR) 算法。文献[4]将LEO卫星模拟成有限状态自动机,每个状态对应于LEO卫星网络系统周期中的一个等长度时间间隔,从而将LEO卫星网络的动态链路分配问题等效成一组静态网络拓扑结构下的固定链路分配和路由优化问题。文献[5]第一次提出了快照(snapshot)的概念,一旦任意ISL临时断开或重新连接,一个不同于先前的快照就形成了,每一个快照对应一个特定时刻的卫星网络拓扑;在此基础上,针对卫星存储能力有限问题,提出了一种程序存储模型来存储必要的路由表,从而节省了卫星的存储空间。为了描述卫星网络快照的变化规律,Wang等人[6]给出了LEO卫星网络快照数目与快照长度的理论计算公式,Fischer等[7]完成了快照概念的形式化描述。然而,以上研究主要针对特定卫星网络中的特定问题,没有对诸如网络最短路径、哈密顿(Hamilton)回路、最大流等基础问题进行分析, 因此不能将上述研究中得到的结论直接应用到所有卫星网络中。
在传统地面网络中,基于时变拓扑的最短路径问题已得到一定程度的关注[8],并提出了一些基于图论优化理论求解最短路径问题的方法和算法[9-11]。然而,已有研究虽然考虑了网络拓扑和链路权值的时变性,但均是针对地面中不同类型的时变网络,不能完全应用到卫星时变拓扑网络中,如:文献[9]主要解决的是随机时变神经网络中的最短路径问题,文献[10-11]主要研究了城市交通时变网络中的最短路径问题。目前,对于卫星网络中的最短路径问题的研究较少,文献[12]通过将卫星时变拓扑网络模型离散化,利用离散卫星网络模型来解决传统迪杰斯特拉(Dijkstra)算法在卫星时变网络中不能直接应用的问题;文献[13]将LEO时变卫星网络分为T/Δt个静止子网,在每一个固定不变的子网中计算源节点卫星到其他节点卫星的最短路径,从而得到[T·n(n-1)]/2Δt条最短路径,然后将这些最短路径分成n张路由表,再将这些路由表通过移动代理分发到n个卫星中。但是,在链路频繁切换的卫星网络中,离散时间片大小的选取直接影响到路由的计算量和路由的有效性,以致当拓扑结构发生改变时,路由算法不能及时地做出相应的处理,在卫星失效的情况下,网络不能正确传输处理信息,从而造成信息丢失。
针对以上问题,本文基于LEO卫星时变网络,通过引入连接计划(contact plan, CP)[14-15]的概念完成了卫星网络时变拓扑的定量描述,进而提出了一种基于CP的最短路径算法(CP-Dijkstra)。与传统基于虚拟拓扑策略的卫星网络路由算法不同的是,本文引入了CP来代替卫星离散化模型进行最短路径的优化设计和计算。节点在发送信息前,会检查当前时刻的CP 是否发生改变,如果没改变,则直接用信息中保存的最短路径继续转发;如果检查到CP发生改变,则在此节点重新计算信息到目的节点的最短路径,并覆盖信息中保存的最短路径,利用新的路径进行转发,直至到达目的节点。从而,保证了CP-Dijkstra算法在卫星链路发生切换时,也能正确计算最短路径,改善了卫星网络的性能。
1 系统模型
LEO卫星网络模型如图1所示,该系统由N×M颗卫星组成,其中N是卫星轨道数目,M是每个轨道中卫星的数目,卫星的运行周期为T,星间链路连通情况和链路长度随着卫星运行时间的变化而周期性变化。
卫星时变拓扑网络是一个无向图,其链路权值是以时间为变量的周期函数,其数学模型可表示为
(1)
(1)式中:V是卫星节点的有穷非空集合;A是卫星节点间的有限边集;W表示卫星节点vi和vj间的链路权值,可以用链路距离、时延或其他费用来表示。
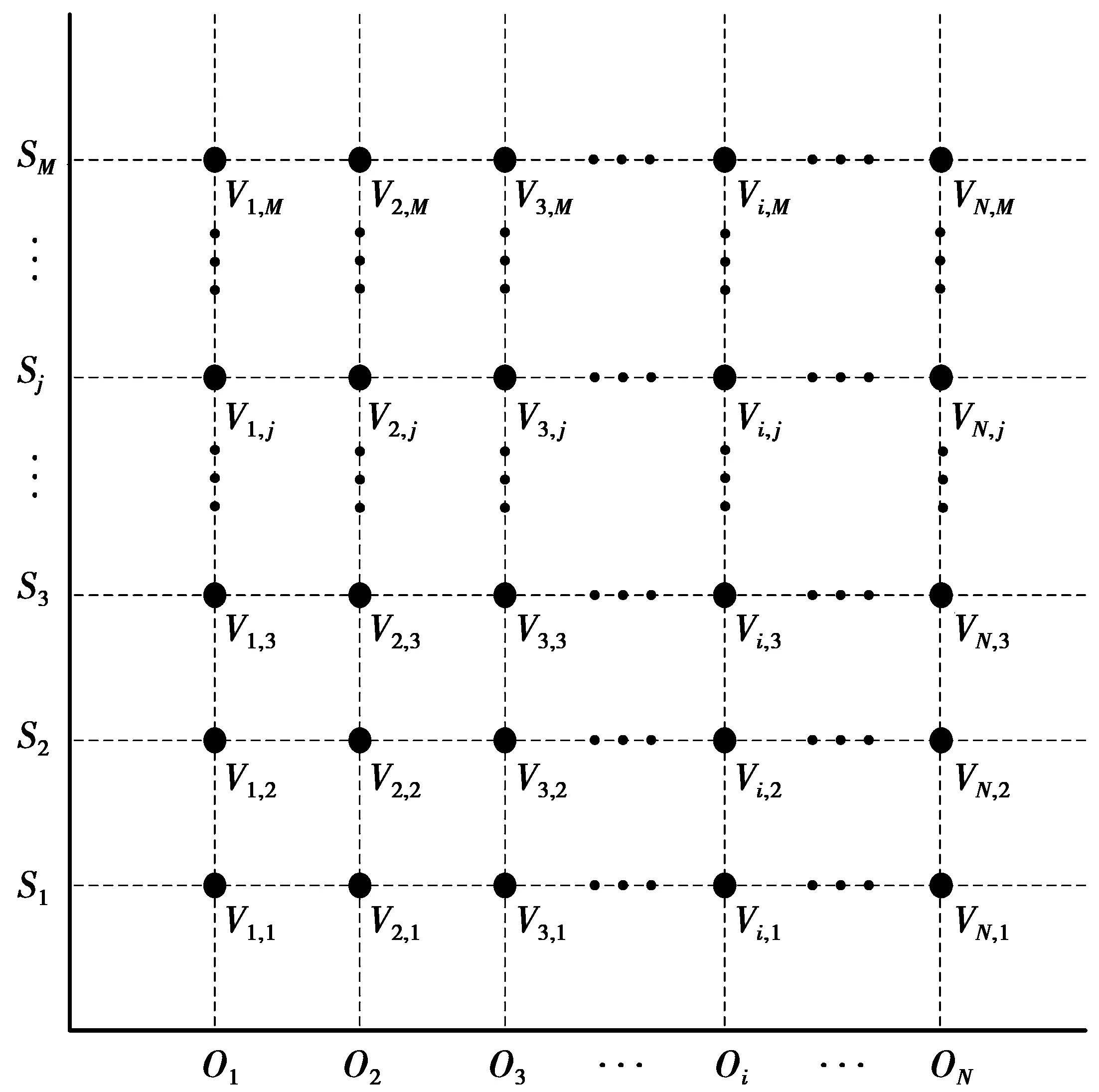
图1 LEO卫星网络模型Fig.1 LEO satellite network model
假设P={v0,v1,…,vd|v0,v1,…,vd∈V}是在卫星网络中从源节点v0到目的节点vd的其中一条路径,则路径P的权值由 (2) 式得到,
(2)
定义1 如果P是从卫星源节点S到目的节点D的其中一条路径,并且网络中其他从S到D的所有路径中没有权值比P的权值更小的路径,则P是卫星节点S到D的最短路径。
随着卫星运行的时间变化,不同时刻星间链路连接情况A(t)可以描述为
(3)
(3)式中:ai,j(t)表示卫星网络中任意2颗卫星vi和卫星vj间的链路通断情况,可由(4)式计算得到。
(4)
(4)式中,(Ni,Nj)∈N,(Mi,Mj)∈M。
同时,W(t)的值随着卫星运行时间变化呈现周期性的变化,本文中W(t)代表星间链路距离,可表示为
(5)

图2 星间链路变化情况Fig.2 Variation of ISLs
2 CP-Dijkstra算法
2.1 问题描述
在地面固定拓扑网络中,节点间的链路发生切换的概率较低,最短路径算法的计算结果准确度较高。但是,在卫星时变拓扑网络中,由于卫星移动速度快,导致星间链路会频繁切换,如果直接应用传统的最短路径算法,在一些情况下不能计算得到正确的最短路径,从而导致信息不能正确转发到目的节点,使得网络性能大幅下降。
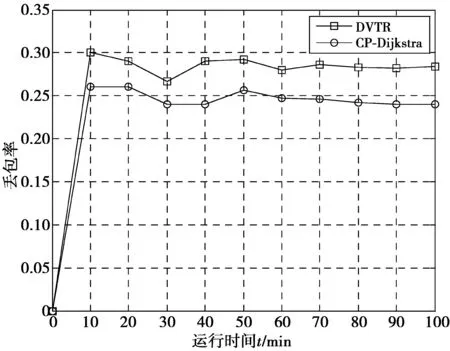
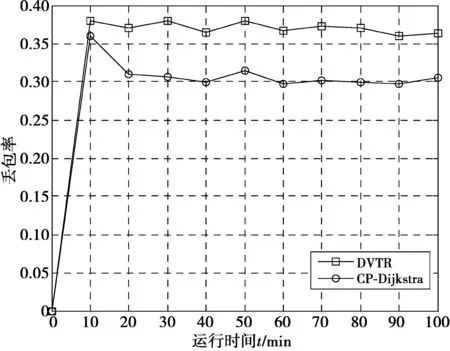
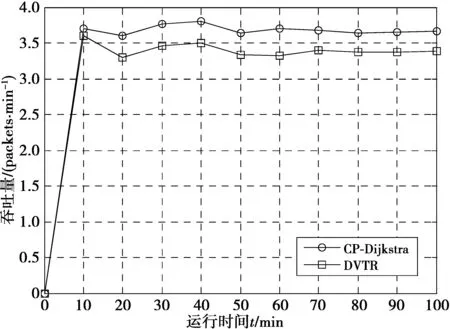
图3给出了卫星时变网络中Dijkstra算法的问题分析,当信息要从源节点S传输到目的节点D,节点b和节点c间的链路在t2时刻会发生切换,节点b的邻居节点由c变为f,此时,Lb,c=∞,节点a在t1时刻会有一条直接链路到达e,La,e 1)当信息在t2时刻到达节点b时,由于星间链路的切换导致Lb,c=∞,此时,信息无法转发到目的节点,造成信息丢失; 2)当信息在t1时刻到达节点a时,星间链路的切换导致节点a与节点e之间存在直接链路,并且La,e 因此,传统最短路径Dijkstra算法应用在卫星时变拓扑网络中时,会出现因星间链路频繁切换导致无法时刻保证路径最优的问题。 图3 卫星时变网络中Dijkstra算法问题分析Fig.3 Problem analysis of Dijkstra algorithm in satellite time-varying network 2.2 卫星时变网络中的连接计划 由以上问题分析描述可知:由于卫星网络拓扑的动态变化,造成星间链路的频繁切换,进而导致Dijkstra算法计算得到的结果不能保证是最优解。通过研究分析卫星确定的运动规律,假设连接机会是计划好或者规划好的,而不是通过预测或者发现的[16],那么利用卫星连接信息和距离信息可以生成一条连接计划,所有的连接计划构成一张连接计划表,将卫星时变网络拓扑用一张连接计划表来描述。每一条连接计划包括连接的源节点、目的节点、起始时间、结束时间以及通信距离等。 例如,图4描述了一个简单的卫星网络拓扑,存在3条连接:卫星节点S1和S2在t1到t4时间段内的一条连接;卫星节点S2和S3在t2到t5时间段内的一条连接;卫星节点S3和S4在t3到t6时间段内的一条连接。首先,通过连接表可以得到卫星在每一个时刻的连接计划,即:当前时刻的卫星网络拓扑结构以及权值等。然后,通过当前时刻的连接计划,利用Dijkstra算法可以计算得到当前时刻的最短路径,进而进行信息转发。 在路由算法开始计算前,连接表会提前分发到各个卫星节点中。由于卫星网络中,卫星节点只跟邻居节点有链路连接,与其他节点均没有直连链路,因此根据连接表可以计算得到每个节点在每个时刻的邻居节点集,利用邻居节点集来进行Dijkstra路由算法计算,可以降低卫星有限的计算能力和节省卫星中有限的存储空间。 图4 卫星时变网络中的连接计划示例Fig.4 Example of contact plan in satellite time-varying network 2.3 基于连接计划的最短路径优化算法步骤 在信息发送之前,根据当前时刻连接计划,利用Dijkstra算法计算出从源节点S到目的节点D的一条最短路径,连接计划随着时间的变化会不断更新,因此信息在不同时刻的转发路径也会不一样,不能用过去存在的连接来转发信息,因此当信息转发到下一跳节点时,下一跳节点会判断节点间的连接计划是否发生改变,如果连接计划没有改变,则根据上一节点计算出的最短路径继续转发到后面的节点,反之,如果在下一跳节点检查到连接计划发生改变,则在下一跳节点根据当前的连接计划重新计算一条新的到达目的节点的最短路径,直到信息到达目的节点。通过这一系列的路径序列,从而可以组成源节点到目的节点的最短路径。具体算法流程如下: 步骤1 由于卫星的运动规律具有确定性的特点,因此在路由算法计算之前,首先根据连接信息(连接起始时间、连接结束时间、发送节点、接收节点、通信速率)和距离信息(连接起始时间、连接结束时间、发送节点、接收节点、通信距离)生成连接计划表,并提前分发给卫星网络中所有的节点。 步骤2 通过连接计划表计算出节点在每一时刻的邻居节点集。当t时刻源节点S产生信息m时,节点S根据t时刻的连接计划,利用节点的邻居节点集来进行Dijkstra算法计算,生成一条到达目的节点D的最短路径,并保存在信息m中进行转发。 步骤3 当信息根据源节点计算的最短路径从源节点转发到下一跳节点A时,此时节点A会根据连接计划是否发生改变对信息做如下2种处理: ①如果节点A检查到连接计划没有发生改变,则按照信息中保存的最短路径继续转发到下一跳节点; ②如果节点A检查到连接计划已发生了改变,则在节点A根据当前连接计划重新计算一条新的到达目的节点D的最短路径,并覆盖原来保存的最短路径,按照新的最短路径进行信息转发到下一跳节点。 步骤4 在后面的节点中重复步骤3的操作,直到信息m到达目的节点D,此时信息m所经过的一系列路径序列即可组成其最短路径。 为了验证CP-Dijkstra算法性能,本文使用卫星工具包 (satellite tool kit, STK)和MATLAB仿真软件进行了联合仿真。仿真中设置了2种不同负载业务流的网络场景:轻负载业务流网络场景和重负载业务流网络场景。在2种不同的网络场景下,令发包速率分别为5 packets/min和10 packets/min,通过与卫星网络中普遍采用的动态虚拟拓扑路由算法(dynamic virtual topology routing, DVTR) 在吞吐量、丢包率和平均时延等性能方面的对比分析,比较2种算法在卫星时变网络中的准确性、有效性等。DVTR算法的基本思想是:首先,将卫星周期等分为若干个时间片,每一个时间片对应一个静态拓扑;然后,在静态拓扑中计算最短路径。 表1 仿真参数设置 图5和图6分别给出了轻、重负载下2种算法的丢包性能,由图5、图6可知重负载下2种算法的丢包率性能均要高于轻负载的情况,而DVTR算法的增幅较大,这是因为在重负载网络场景中,包的发送速率较快,而DVTR算法在链路切换时刻计算不准确时,源节点计算的路由失效导致信息丢失数较多。同时,图5和图6也分别比较了DVTR算法和CP-Dijkstra算法的丢包率在不同负载、不同时刻的变化情况。当运行时间为0时,卫星网络中没有信息产生,丢包率为0;随着卫星运行时间的增加,2种算法的丢包率均稳定在一定的范围内变化。而2种算法的丢包率在不同时刻会起伏变化,这是由于星间链路的切换会导致丢包率的变化。如图5、图6所示,CP-Dijkstra算法的丢包率在任意时刻均要低于DVTR算法,因为DVTR算法使用固定时间间隔Δt将卫星周期离散化,当链路切换时刻发生在Δt之外(两离散间隔之间)时,此时如果信息按照Dijkstra算法计算出的最短路径进行转发,由于节点间的链路不存在,信息不能转发到下一跳节点,从而将会导致信息无法准确到达目的节点,其丢包率会大大增加。 图5 轻负载业务流网络中的丢包率性能Fig.5 Performance of packet loss probability in light load traffic network 图6 重负载业务流网络中的丢包率性能Fig.6 Performance of packet loss probability in heavy load traffic network 图7、图8分别给出轻、重负载下2种算法的吞吐量性能,由图7和图8可知,无论是DVTR算法还是CP-Dijkstra算法,在重负载网络场景中的吞吐量性能都增大,CP-Dijkstra算法稍为明显,这是由于在卫星节点高速移动的情况下,即网络拓扑频繁变化时,DVTR算法路由计算不一定准确,且在短时间内不能及时建立新的有效路由,从而导致在同一时刻,采用CP-Dijkstra算法的网络在重负载情况下收到的信息数更多。同时,图7和图8也分别显示了随着卫星运行时间的变化,DVTR算法和CP-Dijkstra算法的吞吐量的变化情况。如图所示,在同一时刻,DVTR算法的吞吐量性能总是低于CP-Dijkstra算法。这是由于DVTR算法采用的是静态拓扑路由计算方法,该方法不能准确的处理链路切换问题,最短路径算法在链路的连接发生变化后的计算结果不能完全适用,导致信息在转发过程中不能通过计算得到的最短路径转发到下一跳而丢失,从而目的节点不能收到发送的信息。因此,相比较于CP-Dijkstra算法,其吞吐量有所降低。 图7 轻负载业务流网络中的吞吐量性能Fig.7 Performance of throughput in light load traffic network 图8 重负载业务流网络中的吞吐量性能Fig.8 Performance of throughput in heavy load traffic network 图9、图10分别给出了轻、重负载下2种算法的平均时延性能,由图9和图10可知,在重负载网络中,两种算法的平均时延均有所增大,而DVTR算法的平均时延性能表现的更差,这是因为具有高速移动特性的卫星节点会导致链路的频繁中断,DVTR算法不能保证所有信息的转发路径在不同时刻一定处于连通状态,从而使得源节点重新计算路由,导致部分节点不能及时处理消息,使得节点负载过重而丢弃信息造成更大的时延。图9和图10分别对DVTR算法和CP-Dijkstra算法的平均时延进行了比较。当运行时间为0时,卫星网络中没有产生任何信息,因此平均时延为0;随着运行时间的变化,网络中信息数量会不断增加,两种算法的网络的平均时延变化均稳定在一定范围内。如图所示,由于DVTR算法在星间链路频繁切换时,计算的最短路径不一定正确或是最优,当计算得到的最短路径中的链路发生切换,信息不能及时转发到下一跳,从而需要等待至少一个周期之后,才能将信息转发到最短路径中的下一跳节点,因此导致其平均时延要高于CP-Dijkstra算法。 图9 轻负载业务流网络中的平均时延性能Fig.9 Performance of average delay time in light load traffic network 图10 重负载业务流网络中的平均时延性能Fig.10 Performance of average delay time in heavy load traffic network 本文针对LEO卫星时变网络,提出了一种基于连接计划的最短路径Dijkstra优化算法,在信息传输前,节点首先会判断连接计划是否发生改变,如果没有改变,则利用之前已计算好的最短路径进行信息转发;否则,节点会根据当前时刻的连接计划重新计算一条最短路径,从而更新之前节点计算得到的最短路径,并将其保存到信息中,此时信息将会按照新的最短路径进行转发,直到信息到达目的节点。仿真结果表明,采用CP-Dijkstra算法不仅提高了网络的吞吐量,而且降低了网络丢包率和平均时延。 [1] HONG S G, SU C J. ASAP: fast, controllable, and deployable multiple networking system for satellite networks[C]// IEEE Global Communications Conference (GLOBECOM). San Diego, CA: IEEE, 2015:1-7. [2] WAN Peng, YE Jianshe, SONG Shijie. Study on the telecommunication technology based on the distributed satellite constellation networks[C]// IEEE Aerospace Conference. Big Sky, MT: IEEE, 2014:1-8. [3] WERNER M. A dynamic routing concept for ATM-based satellite personal communication networks [J]. IEEE Journal on Selected Areas in Communications, 1997, 15(8):1636-1648. [4] CHANG H S, KIM B W, CHANG L, et al. FSA-based link assignment and routing in low-earth orbit satellite networks [J]. IEEE Transactions on Vehicular Technology, 1998, 47(3):1037-1048. [5] GOUNDER V V, PRAKASH R, ABU-AMARA H. Routing in LEO-based satellite networks[C]// IEEE Proceedings of Emerging Technologies Symposium, Wireless Communications and Systems. Richardson, TX: IEEE, 1999:22.1-22.6. [6] WANG Junfeng, LI Lei, ZHOU Mingtian. Topological dynamics characterization for LEO satellite networks [J]. Computer Networks, 2007, 51(1):43-53. [7] FISCHER D, BASIN D, ECKSTEIN K, et al. Predictable mobile routing for spacecraft networks [J]. IEEE Transactions on Mobile Computing, 2013, 12(6):1174-1187.[8] AHUJA R K, MAGNANTI T L, ORLIN J B. Network flows: theory, algorithms, and applications [M]. Englewood Cliffs, New Jersey: Prentice Hall, 1993. [9] 闫春望,黄玮,王劲松.一种随机时变神经网络最短路径算法[J].天津理工大学学报,2016,32(2):40-44. YAN Chunwang, HUANG Wei, WANG Jinsong. A stochastic time-varing neural network shortest path algorithm [J]. Journal of Tianjin University of Technology, 2016, 32(2):40-44. [10] ROSYIDI L, PRADITYO H P, GUNAWAN D, et al. Time-base dynamic weight for Dijkstra algorithm implementation in route planning software[C]// International Conference on Intelligent Green Building and Smart Grid. Taipei: IEEE, 2014:1-4. [11] WEI Mingjun, MENG Yu. Research on the optimal route choice based on improved Dijkstra[C]// IEEE Workshop on Advanced Research and Technology in Industry Applications. Ottawa, ON: IEEE, 2014:303-306. [12] DONG Xiangjun, SHI Haoshan. A shortest path algorithm based on mobile agent in LEO satellite network[C]// IEEE International Conference on Wireless Communications, Networking and Mobile Computing. Dalian: IEEE, 2008:1-5.[13] 张涛, 柳重堪, 张军. 卫星时变拓扑网络最短路径算法研究[J]. 计算机学报, 2006, 29(03):371-377. ZHANG Tao,LIU Zhongkan,ZHANG Jun.A shortest path algorithm for satellite time-varying topological network [J].Chinese Journal of Computers,2006,29(03):371-377.[14] FRAIRE J A, FINOCHIETTO J M. Design challenges in contact plans for disruption-tolerant satellite networks [J]. IEEE Communications Magazine, 2015, 53(5):163-169.[15] ARANITI G, BEZIRGIANNIDIS N, BIRRANE E, et al. Contact graph routing in DTN space networks: overview, enhancements and performance [J]. IEEE Communications Magazine, 2015, 53(3):38-46. [16] BURLEIGH S. Contact graph routing, IRTF, Internet-Draft draft-burleigh-dtnrg-cgr-01, Experimental [EB/OL]. (2010-07-08) [2016-07-20]. https://tools.ietf.org/html/draft-burleigh-dtnrg-cgr-01. (编辑:魏琴芳) Contact plan based the shortest path optimization algorithm in satellite time-varying networks DAI Cuiqin, LI Jian, TANG Huang (Key Lab of Mobile Communications Technology, Chongqing University of Posts and Telecommunications, Chongqing 400065, P. R. China) Aiming at the problem that Dijkstra shortest path algorithm cannot always ensure the optimal path in satellite time-varying topological network, this paper proposes a shortest path algorithm based on CP (CP-Dijkstra) by considering the determinacy of satellite node movement, researching and analyzing the periodicity dynamic change of satellite network topology. In LEO satellite systems, firstly dynamic CP is formed according to the time-varying connection of inter satellite links at different time. And then, the satellite node checks whether the CP is updated or not to chooses different methods to deal with the message: When the CP is not updated, the message will be forwarded with the shortest path calculated by the previous node; otherwise, the node will calculate a new shortest path to the destination node according to the CP at the present time, until the message is successfully forwarded to the destination node. With this scheme, a series of path where the message has gone through is named the shortest path. Simulation results show that the CP-Dijkstra algorithm can not only improve the throughput of the network, but also effectively reduce the average delay and packet loss probability compared with the commonly used DVTR algorithm in the satellite time-varying network. satellite time-varying network; the shortest path algorithm; contact plan; throughput; packet loss probability 10.3979/j.issn.1673-825X.2017.01.005 2016-08-02 2016-12-10 通讯作者: 戴翠琴 daicq@cqupt.edu.cn 国家自然科学基金(61601075);重庆市科委自然科学基金(cstc2016jcyjA0174);重庆市教委自然科学基金(KJ1500440);长江学者和创新团队发展计划(IRT16R72) Foundation Items:The National Natural Science Foundation of China (61601075); The Natural Science Foundation Project of CQ CSTC (cstc2016jcyjA0174); The Scientific and Technological Research Program of Chongqing Municipal Education Commission (KJ1500440); The Program for Changjiang Scholars and Innovative Research Team in University (IRT16R72) TN929.5 A 1673-825X(2017)01-0029-07 戴翠琴(1976-),女,宁夏固原人,副教授,主要研究方向为宽带无线通信网络关键技术。E-mail 地址:daicq@cqupt.edu.cn 李 剑(1992-),男,安徽安庆人,硕士生,主要研究方向为卫星通信中的路由算法。E-mail 地址:562925078@qq.com 唐 煌(1993-),男,重庆渝北人,硕士生,主要研究方向为卫星时变网络中的路由算法优化。E-mail地址:449325126@qq.com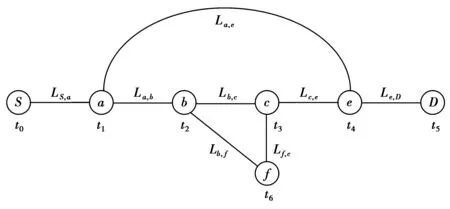

3 仿真分析
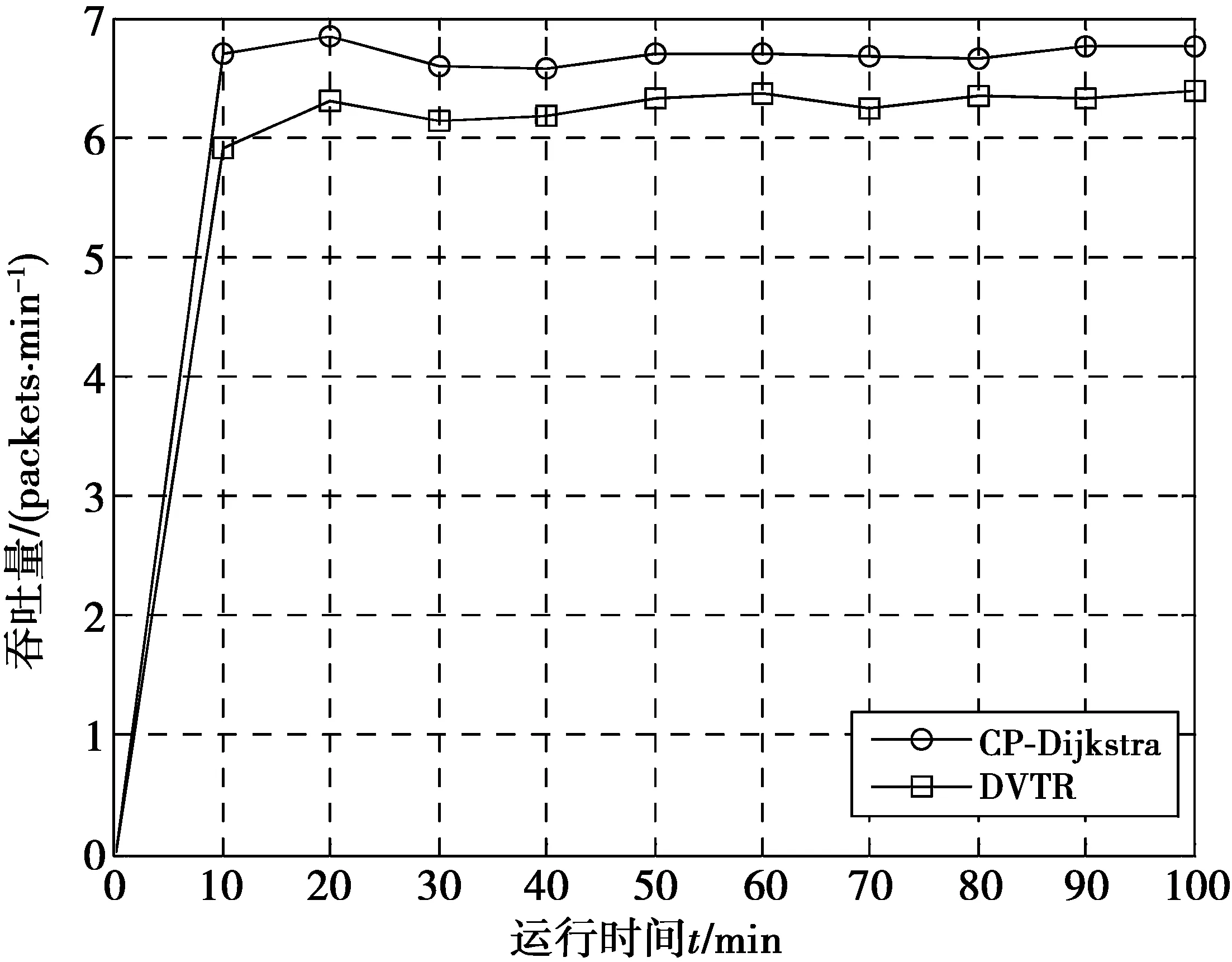
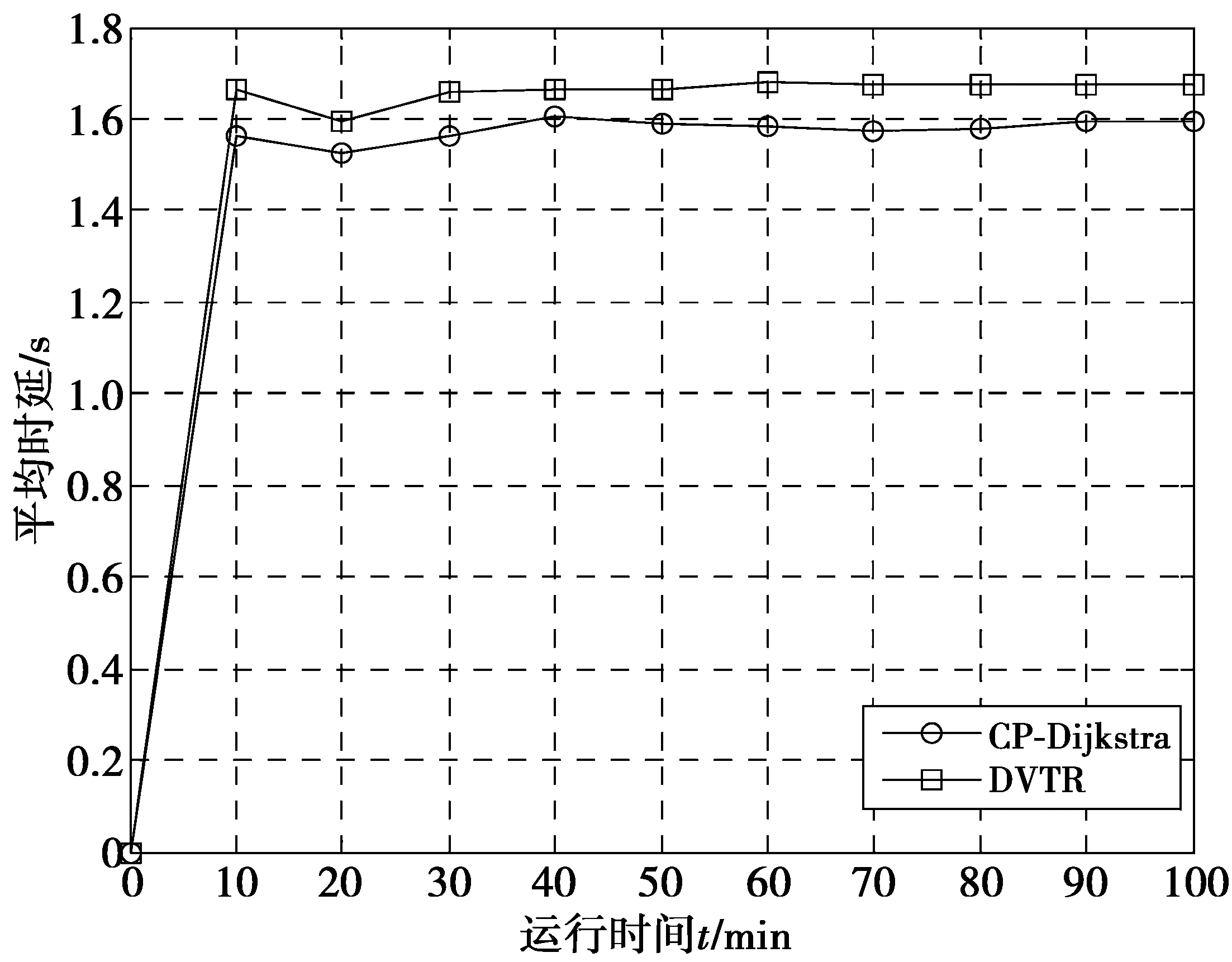
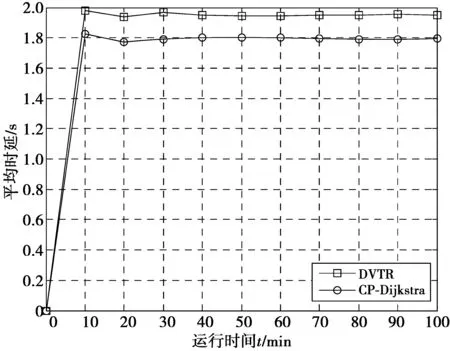
4 结束语



