常数轮公平理性秘密共享方案

李梦慧，田有亮，冯金明

（1. 贵州大学数学与统计学院，贵州 贵阳 550025；2. 贵州大学密码学与数据安全研究所，贵州 贵阳 550025；3. 贵州省公共大数据重点实验室，贵州 贵阳 550025；4. 贵州大学计算机科学与技术学院，贵州 贵阳 550025)

常数轮公平理性秘密共享方案

李梦慧1,2，田有亮2,3,4，冯金明1,2

（1. 贵州大学数学与统计学院，贵州 贵阳 550025；2. 贵州大学密码学与数据安全研究所，贵州 贵阳 550025；3. 贵州省公共大数据重点实验室，贵州 贵阳 550025；4. 贵州大学计算机科学与技术学院，贵州 贵阳 550025)

在理性秘密共享方案中，公平性是所有参与者期望的目标。基于均匀分组原理研究了常数轮理性秘密共享方案，结合双线性对有关知识和双变量单向函数构造知识承诺方案，该方案是可验证的，以此来检验分发者和参与者的欺骗问题。分发者分给各组参与者的子秘密份额数量最多相差1，有效约束参与者的偏离行为。参与者按照协议执行4轮即可实现公平重构秘密，一定程度上降低了公平理性秘密共享方案的通信复杂度，具有一定应用价值。

秘密共享；通信复杂度；博弈论；双线性对

1 引言

秘密共享方案是分布式密码协议的基础。秘密共享方案的公平性指要么所有参与者都能获得共享秘密，要么都得不到秘密。公平性最早的研究可以追溯到Even等[1]的工作，他们非正式地证明了电子签名交换是不可行的。Ong等[2]提出一个适用于任何门限秘密共享方案的秘密重构协议，并且证明了当存在少数诚实参与者和绝大多数理性参与者的情况下，该协议是公平的，参与者两轮就可重构秘密。Lee[3]提出了公平的理性秘密共享方案，其中恶意参与者的数量，该方案采用异步广播信道，最终参与者有相同的概率重构出秘密。Tian等[4]研究秘密共享协议的公平性问题，提出公平的秘密分发和重构方案，分别在 3种攻击模型下证明了方案的公平性和安全性。Cai等[5]提出理性秘密共享协议，解决了协议

的公平性问题。Damgard等[6]针对贿赂的情况，设计了一个三轮协议，并保证了公平性，协议要求私密的点对点通道，但是建立这些需要额外增加轮数。2012年，Asharov等[7]提出著名的五轮协议，并且保证了公平性。在拥有少数恶意者的多方情况下，Garg等[8]提出一个两轮协议，但是该协议没有保证公平性。2014年，De等[9]通过引入包括获得秘密的效用和计算产生的花费的混合效用模型，提出了针对偏好尽可能少的通信和计算量的“silent”成员及偏好最大化自身利益的“non-silent”成员的分发者公平理性秘密共享方案，该方案的通信复杂度与秘密分发者选取的参数β有关。随后，Gordon等[10]指出保证输出传递的三轮协议要比实现公平性困难，提出了门限全同态加密方案，允许参与者将弹性密文改变为非中止方的公钥，不用增加额外的轮就可以处理参与者的中止行为。2015年，刘海等[11]基于重构顺序调整机制提出公平理性秘密共享方案，该方案基于秘密分发者随机选取重构轮数，设计具有未知重构轮数的理性秘密共享方案，有效约束了参与者的自利行为，并且该方案实现了子博弈完美均衡。

针对理性秘密共享方案的公平性问题，结合双线性对有关知识设计知识承诺方案和双变量单向函数构造可验证的秘密共享方案，基于均匀分组原理将参与者分为每 3人一组，采用未知轮数思想进行秘密重构，并通过组间比较得到真正共享秘密。通过与现有公平理性秘密共享方案的对比分析，说明本文所提方案不仅可以实现公平性与安全性，而且通信复杂度更低、实用性更强。

2 基本知识

本节主要介绍双变量单向函数、双线性映射、效用函数和扩展式博弈相关知识。

定义1 双变量单向函数。

若 E = f( x, y)满足以下6个性质，则称其为双变量单向函数。

1) 给定x、y容易计算出 E = f( x, y)。

2) 给定x和E，很难计算出y的值。

3) 不知道y时，对任意的x，很难计算出E的值。

4) 给定y，很难找到 2个不同的 x1, x2使f( x1, y) = f( x2,y)。

5) 给出x和E，很难计算出y。

6) 给出 x1和 f( x1, y)，很难计算出 f( x2, y)的值。

定义2 双线性映射。

设 G1和 G2分别是阶为素数q的加法群和乘法群，P是G1的一个生成元。若映射 e: G1×G1→G2满足以下3个条件则称映射e为双线性映射。1) 双线性。对 ∀ P, Q ∈ G1, a, b ∈有e( a P, bQ ) = e( P, Q )ab。

2) 非退化性。若P是 G1的生成元，则 e( P, P)是 G2的生成元，即e( P, P)≠ 1。

3) 可计算性。对 ∀ P, Q ∈ G1，总存在有效的算法计算 e( P, Q)。

定义3 双线性Diffie-Hellman问题（BDHP）。

在 (G1, G2, e)中，给定(P, a P, b P, c P)，对任意的a, b, c ∈，计算 e( P , P )abc∈ G2。

BDH假设：在求解BDH问题上，不存在PPT算法有不可忽略的优势。

定义4 效用函数。

在理性秘密共享协议中，理性参与者根据利益最大化采取行动，即基于每一步收到的所有信息决定其行动策略。本文定义理性参与者 Pi的效用函数 u:{0,1}n→ S,S表示秘密重构后所有可

i RR能的结果。向量 O :(o, o ,… ,o )∈ {0,1}n表示所有12n理性参与者秘密重构的一个结果。当且仅当 oi=1时，理性参与者 Pi得到了共享秘密，否则 oi= 0。理性参与者 Pi效用函数 ui满足：

1) 对 ∀ O, O ′∈{0,1}n，如果oi＞ oi′ ，则 ui(O)＞ui(O ′)；

2) 如果 oi=oi′ 且则ui(O)＞ ui(O ′)。

因此，对理性参与者 Pi来说，首先，他想要独得秘密；其次，想要更少的其他参与者得到秘密。本文用以下4种情况表示 Pi收益。

1) ui= U+表示理性参与者 Pi独得共享秘密获得的收益。

2) ui= U表示所有人都得到秘密时 Pi的收益。

3) ui= U−表示所有人均没有得到秘密时 Pi的收益。

4) ui= U−−表示 Pi没有得到秘密，其余人均得到秘密时的收益。

定义5 扩展式博弈。

扩展式博弈是一个六元组 G ={P, A, H,F, I, U }，具体描述如下。

1) P = {P1, P2,… ,Pn}表示理性参与者集合，其中，Pi表示第i( i = 1,2,… ,n)个理性参与者，P-i表示除了理性参与者 Pi外其余所有理性参与者的集合。

2) A = {A1, A2,… ,An}表示n个理性参与者的策略集。其中， A = {a1, a2,… ,ak}是理性参与者P

iii ii的策略集，∈ A( i = 1,2,… ,k )是理性参与者P的ii第j种策略， a = (a1, a2,… ,an)表示每一个理性参与者选择一个策略 ai∈ Ai(1 ≤i≤ n)组成的策略组合。除理性参与者Pi外，其余理性参与者的策略组合表示为 a−i= (a1, a2,… ,ai−1,ai+1,… ,an)。策略组合a = (a1, a2,…,an)和 a ′= (a1′, a2′,… ,an′ ), (ai′, a−i)= (a1,…,ai−1,ai′, ai+1,… ,an)表示理性参与者 Pi的行动策略为 ai′，其余理性参与者策略组合为 a-i= (a1,…, ai−1,ai+1,…,an)。

3) H表示历史序列集合。h ={ak}k=1,2,…,K∈H表示长度为K的历史。对 ∀h ∈ H,h随后可能出现的所有策略组合用 A( h )= {a |(h, a )∈ H}表示，若 A( h)=∅，那么历史序列h是终止的，Z表示所有终止节点组成的集合。

4) F: H/ Z → P表示为非终止历史 h ∈H/ Z指定下一步采取行动的理性参与者。

5) I = {I1, I2,… ,In}表示信息分割的集合，其中， I= {I1,I2,… ,IK}表示理性参与者P对历史iii ii{h ∈ H| F( h) = P}的信息集。如果 h, h ′ ∈ Ij(1≤i i j≤ K)，当理性参与者处在同一信息集中时，有A( h ) = A( h′)。

6) U = {u1, u2,… ,un}表示n个理性参与者的效用函数的集合。 ui表示理性参与者 Pi的效用函数。 ui( a)表示当参与者采取策略组合a时， Pi的效用。

定义6 纳什均衡。

在博弈三元组 Γ={N, S, U}中，策略组合a =(a1, a2,… ,an)∈A 是Γ的一个纳什均衡，如果对理性参与者 Pi( i = 1,2,…, n)，所有的ai′∈ A，都有ui( a )≥ ui( ai′, a−i)成立。

3 公平理性秘密共享方案

3.1 参数假设

本方案假设秘密分发者D要在n个理性参与者 Pi( i = 1,2,… ,n)间共享秘密 S ∈,一个公开可见的公告板B用于记录公开信息，Ui表示重构结束后，除惩罚值外，理性参与者 Pi获得的收益。

3.2 惩罚机制

在理性参与者重构秘密过程中，若发生偏离协议的行为，则该参与者将会得到一个公开的惩罚值 Up＜ 0，被记录在公告板上，并且协议终止。

定义7 惩罚机制。

如果 Pi公开的是假份额，则 Pj( j ≠ i)向其余所有理性参与者广播 Pi是欺骗者, 并在公告板上记录下对 Pi的惩罚值注：协议开始前每个参与者均没有获得惩罚值。定理1 定义 7所述惩罚机制为激励相容机制。

证明 若理性参与者 Pi偏离协议，根据惩罚机制， Pj( j ≠ i)会在公告板B上记录对 Pi的惩罚值且协议终止，即使 Pi能获得秘密，但其得到一个公开的惩罚值，使其最终收益小于U，这与理性参与者追求自身利益最大化相矛盾。因此，理性参与者按照协议执行是最佳策略。所以，本文利用的惩罚机制是激励相容机制。

3.3 秘密分发协议

Step1 秘密分发者D，将理性参与者n每3个人分为一组，共k组（这里只考虑n为3的整数倍的情况），即计算= k，随机选取r*∈ (1,k)，记= S,在集合中随机选取 k− 1个整数，分别记为

Step2 秘密分发者 D计算并公开对所有 Si的承诺 Ci0= C( Si)= e( SiP, P + Q)，其中i= 1,2,… , k。

Step3 秘密分发者 D利用双变量单向函数E = F( x, y)，计算 Ei= F( Si, y)，并公开 Ei和y，其中 i= 1,2,…, k。

Step4 秘密分发者 D 随机选取 ai0,ai1, a∈ Z*,i = 1,2,… , k ，构造多项式 f( x)= a +

i2q ii0a x + a x2，其中 a = S。计算并公开对系数的

i1i 2i0i承诺 Cij= C( aij)，其中 j= 1,2。

Step5 秘密分发者D随机选取 gil(x )= bil0+ b x + b x2, l = 1,2,3，计算C =C( r )=e( r P,

il1il2il0il0il0P + Q)，其中 ril0= bil0，计算并公开对系数的承诺Cilj= C( bilj)，其中， j= 1,2。

Step6 秘密分发者D计算每个多项式的值，分别标记为 (ri11,ri12,ri13) =(gi1(1),gi1(2),gi1(3)), (ri21,ri22,ri23) =(gi2(1),gi2(2),gi2(3)),(si1, si2,si3)=(fi(1), fi(2),fi(3)),(ri31,ri32,ri33) =(gi3(1),gi3(2),gi3(3))。

Step7 秘密分发者D将子秘密份额 (ri11,ri21, si1)、 (ri12,ri22,si2)、 (ri13,ri23,si3,ri33)分别分发给第i组中的3个理性参与者，且每个理性参与者只知道自己和其他参与者的份额数只相差 1，理性参与者得到份额后可利用

验证份额的正确性(m = 1,2,3)。

3.4 秘密重构协议

在得到分发者分发的秘密份额后，参与者只知道自己的份额与其他成员相比至多相差 1，并不知道在第几轮能重构出真正有用的份额。

1) 组内重构协议（第i组 i= 1,2,… , k）

Round1 3个理性参与者分别公开第一个份额 (ri11,ri12,ri13)，利用式(1)验证子秘密份额的正确性，若理性参与者 Pi公开的子秘密份额不正确，则在公告板B上记录 Pi是欺骗者，且给其一个惩罚值 Up，将其剔除出局，协议停止。若正确，则利用拉格朗日差值多项式计算 bi10。

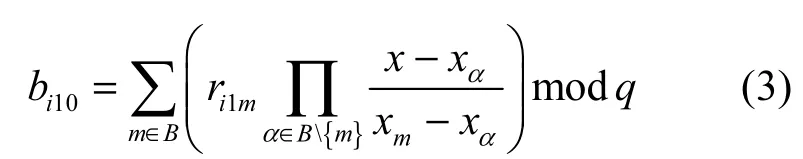
验证 Ei≠ F( bi10,y)，则转入下一轮。

Round2 3个理性参与者分别公开第二个份额 (ri21,ri22,ri23)，利用式(1)验证子秘密份额的正确性，若理性参与者 Pi公开的子秘密份额不正确，则在公告板B上记录 Pi是欺骗者，且给其一个惩罚值 Up，将其剔除出局，协议停止。若正确，则利用拉格朗日差值多项式计算子秘密 bi20。验证 Ei≠ F( bi20,y)，则转入下一轮。

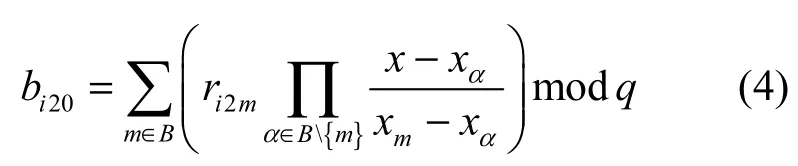
Round3 3个理性参与者分别公开第一个份额 (si1,si2,si3)，利用式(2)验证子秘密份额的正确性，若理性参与者 Pi公开子秘密份额不正确，则在公告板B上记录 Pi是欺骗者，且给予其一个惩罚值 Up，将其剔除出局，协议停止。若正确，则利用拉格朗日差值多项式计算子秘密 ai0。

若验证 Ei= F( ai0,y)成立,则记 ai0= Si,进入组间重构协议。

2) 组间重构协议

k个组各选出一名代表依次在公告板上写下本组在组间重构得到的 Si( i= 1,2,… ,k)，并利用公开的双变量单向函数值及其公开参数，验证该Si是否正确，若第i组公开的是正确的 Si，则第i+ 1组将本组得到的 Si+1公开，当某个 Si满足S1＜S2＜…＜ Si−1＜Si＞ Si+1＞… ＞Sk时，理性参与者将得到共享秘密 Si= Sr*= S。

4 方案分析

下面对本文所提理性秘密共享方案的正确性、安全性和公平性进行分析。

4.1 正确性分析

下面证明式(1)的正确性。

证明 因为 rilm= gil(m)，所以

同理可得式(2)的正确性。

在秘密份额分发阶段，当理性参与者Pi收到秘密分发者 D发送来的子秘密份额，利用式(1)和式(2)验证子份额的正确性，从而防止分发者的欺骗行为。在秘密重构阶段，当Pi得到其他2个参与者的子秘密份额，首先，利用式(1)和式(2)验证其份额的正确性，可以防止理性参与者的欺骗行为，当3个成员都公开正确份额时，可利用拉格朗日差值多项式(3)～式(5)计算出秘密 Si；然后，进行最后一轮组间比较，最大的即为分发者要共享的真正子秘密 S，并且可以利用公告板 B上公开的双变量单向函数的公开值，验证秘密 S的正确性。

4.2 安全性分析

引理1 在上述方案中，对多项式 fi( x)系数ai0,ai1,ai2的承诺 Ci0,Ci1,Ci2是安全的，当且仅当BDH假设成立。

证明 必要性（反证法）。假设本文方案中的承诺函数是安全的，但 BDH假设不成立。因为BDH假设不成立，所以存在一个有效算法A：对群G1中给定的 P, aP, bP, cP( a, b, c ∈ Z)算法 A成功计算出 e( P, P )abc的概率为ε。接下来，证明算法 A可以攻破上述承诺函数。随机选取α, β, γ ,α′, β′, γ ′∈ Z,分别将(P,α P,β P,γ P )和(P,α ′P, β ′P, γ′P)作为算法A的输入，由BDH假设不成立可知，算法 A成功输出 e( P, P)αβγ和e( P, P)α′β′γ′的概率为ε，又因 Cim= e( P, P)αβγ⋅ e( P, P)α′β′γ′，即e( (α βγ) P, P ) =，因此得出 fim，这与承诺函数是安全的相矛盾。所以，如果上述承诺函数是安全的，则BDH假设成立。

充分性（反证法）。假设BDH假设成立，但上述方案中的承诺函数是不安全的。因此，存在有效算法B：将群 G1中的任意元素 Q1, Q2, Q3作为算法B的输入，算法B可以成功计算出 fim的概率为ε，满足 Cim= e( fimP, P +P )= e( Q1, Q2+Q3)。设fim=αP,α ∈ Z和Q1= α1P, Q2= α2P,Q3=α3P(α1, α ,α ∈Z)算法B能成功计算出 f的概率为ε23im且满足 e( α1P ,α2P + α3P )= e(αP, P+P)，即为,令 a =2−1α−1，b= α， c= α + α 则算法B可以123成功计算出 e( P, P )abc，这与 BDH假设成立相矛盾。因此，如果 BDH假设成立，则本文方案中的承诺函数是安全的。

同理可得，对多项式系数 gil(x)系数的承诺也是安全的，当且仅当BDH假设成立。

引理 2 任何理性参与者都不可能伪造一个秘密S*，满足双变量单向函数 E = F( S*,y)。

证明 根据双变量单向函数的6个性质知，任何理性参与者都不可能伪造一个 Si′使F( Si′ , y) = F( Si, y) =Ei。

4.3 公平性分析

对所有理性参与者Pi，分别考虑以下几种情况。

1) 若参与者Pi均按照协议执行，则所有参与者都能得到共享秘密S。

2) 在组内重构阶段，每个参与者不知道自己的份额比其他2个成员的份额数量是多1个还是少 1，最好的策略就是按照协议执行，可得本组的共享子秘密，才会有进入组间重构的机会。若有一个参与者 Pj在此阶段最终重构轮前偏离协议，公开假的子秘密份额，则该参与者不能通过承诺值验证，被剔除出局，并在公告板B上记录Pj是欺骗者，且给Pj一个惩罚值Up，协议结束，所有参与者均没有得到共享秘密。若Pj在最终重构轮偏离协议，将被检测出来，Pj猜中该轮是子秘密重构轮的概率最大为，而其得到的子秘密正好是真正子秘密的概率为，其余组可以经过组内重构得出子秘密，通过求和可以得到真正共享秘密S。此时，所有参与者均得到共享秘密。

3) 在组间重构阶段，若有一个参与者Pj偏离协议，则不能通过承诺值验证，会被剔除出局，并在公告板B上记录Pj是欺骗者，且给Pj一个惩罚值 Up，其猜中自己重构出的秘密是真正秘密的概率为，其他参与者通过求和可得到真正共享秘密S。此时，所有参与者均得到真正共享秘密。

4.4 纳什均衡分析

定理2 如果协议的参与者均是理性的，则在BDH假设下，本文方案可以实现纳什均衡U, U ,… ,U。

证明 在方案中的组内重构阶段，每组内的任意2个理性参与者子秘密份额的数量都不超过1。在本方案中第3轮之前，第i组内的理性参与者 Pi1没有得到组内其他成员的所有子秘密份额，因此，所有成员均会按照协议执行。在最后一轮时，可能会出现以下2种情况。

1) 若组内所有成员的子秘密份额数都相等，在最后一轮，第i组内的理性参与者 Pi1不确定另2个成员 Pi2、 Pi3是否拥有多1个的子秘密份额，为了重构出完整的秘密，理性参与者均会在最后一轮广播真实的子秘密份额。

2) 若组内成员的子秘密份额数量相差1，记第i组内的3个成员分别为 Pi1、Pi2、Pi3其分别拥有的子秘密份额数量分别为 di1、 di2、 di3，设di1=di2= di3−1，在最后一轮，各参与者广播自己的子秘密份额，且期待在下一轮得到组内其他成员的子秘密份额，在下一轮， Pi1、 Pi2已经广播完自己所有的子秘密份额，但此时 Pi3并不知道其他2个成员的子秘密份额已经广播完毕，并且希望得到下一轮 Pi1、 Pi2的子秘密份额。因此，理性参与者要想得到秘密，所有参与者都需按照协议执行。

在组间重构阶段，理性参与者依次在公告板B上公开自己重构的秘密，若第i组理性参与者在此阶段偏离协议，即使其得到真正的秘密份额S，其他参与者可以通过求和得到真正的共享秘密S，并且在公告板上记录第 i组欺骗，给予欺骗者一个惩罚值 Up。此时，欺骗组中的每个成员获得的最终收益为 Ui= U+ Up＜ U。因此，对理性参与者来说，最好的策略就是按照协议执行，并得到最终收益为U。

5 方案对比

在通信复杂度、通信类型、前提假设这3个方面，将本文方案与文献[5,7,9,11]方案进行对比分析，如表1所示，其中，b为分发者随机选取的整数，β表示概率参数，K表示分发者从(2, )Round中随机选取的整数。

表1 本文方案与其他公平理性秘密共享方案对比

由表1可知，在通信复杂度方面，文献[5,9,11]方案的通信轮数都与所选参数有关，文献[7]方案至少为4轮，本文方案仅需4轮即可重构秘密。在维护信道所需开销方面，文献[5,9,11]方案需要单一信道，本文方案需要2个信道，因此开销要比文献[5,9,11]方案稍高，但比文献[7]方案中要维护点对点信道安全所需开销要低的多，且本文方案不需要秘密分发者在线。因此，本文方案更能满足实用性需求。

6 结束语

本文基于重复博弈构造理性秘密共享方案，理性参与者按照协议执行会比偏离协议获得更多的收益。本文方案引入了惩罚机制，能够更好地维护诚实理性参与者的利益，结合承诺方案和双变量单向函数，可以有效地防止秘密分发者和理性参与者的欺骗行为，利用分组思想，可有效降低方案的计算量和通信复杂度，并且该方案实现了公平性。本文方案是在假设没有参与者合谋的情况下构造的，下一步将主要研究抗合谋攻击的理性秘密共享方案。

参考文献：

[1] EVEN S, YACOBI Y. Relations among public key signature schemes[R].Technion Computer Science Department Technical Report CS0175. 1980.

[2] ONG S J, PARKES D C, ROSEN A, et al. Fairness with an honest minority and a rational majority[C]//The Conference on Theory of Cryptography. 2009:36-53.

[3] LEE Y C. A simple (v, t, n)-fairness secret sharing scheme with one shadow for each participant[C]//The International Conference on Web Information Systems and Mining. 2011:384-389.

[4] TIAN Y L, MA J F, PENG C G, et al. Secret sharing scheme with fairness[C]//2011 International Joint Conference on IEEE Trust-Com-11/IEEE ICESS-11/FCST-11. 2011:494-500.

[5] CAI Y Q, PENG X Y. Rational secret sharing protocol with fairness[J]. Chinese Journal of Electronics, 2012, 21(1): 149-152.

[6] DAMGÅRD I, ISHAI Y. Constant-round multiparty computation using a black-box pseudorandom generator[C]//Advances in Cryptology–CRYPTO. 2005: 378-394.

[7] ASHAROV G, JAIN A, LÓPEZ-ALT A, et al. Multiparty computation with low communication, computation and interaction via threshold FHE[C]//Advances in Cryptology–EUROCRYPT. 2012: 483-501.

[8] GARG S, GENTRY C, HALEVI S, et al. Two-round secure MPC from Indistinguish ability obfuscation[M]//Theory of Cryptography. Berlin Heidelberg: Springer, 2014: 74-94.

[9] DE S J, RUJ S, PAL A K. Should silence be heard? fair rational secret sharing with silent and non-silent players[M]//Cryptology and Network Security. Beilin: Springer, 2014:240-255.

[10] GORDON.S, LIU F H, SHI E. Constant-round MPC with fairness and guarantee of output deliver[C]//Advances in Ctyptology- CTYPTO. 2015:63-82.

[11] 刘海, 李兴华, 马建峰. 基于重构顺序调整机制的理性秘密共享方案[J]. 计算机研究与发展, 2015, 52(10):2332-2340. LIU H, LI X H, MA J F. Rational secret sharing scheme based on reconstructed sequential adjustment mechanism [J]. Journal of Computer Research and Development, 2015, 52 (10): 2332-2340.

Constant-round fair rational secret sharing scheme

LI Meng-hui1,2, TIAN You-liang2,3,4, FENG Jin-ming1,2

(1. College of Mathematics and Statistics, Guizhou University, Guiyang 550025, China; 2. Institute of Cryptography & Data Security, Guizhou University, Guiyang 550025, China; 3. Key Laboratory of Public Data of Guizhou Province, Guiyang 550025, China; 4. College of Computer Science and Technology, Guizhou University, Guiyang 550025, China)

In the rational secret sharing scheme, fairness is the goal that all participants expect. Based on the principle of uniform grouping, the scheme was verified by combining bilinear pair knowledge and bivariate one-way function to verify the deception problem of the distributor and the participant.The number of sub-secret shares distributed by the distributor to each group of participants is at most one, effectively restricting the deviation behavior of the participant. In the end, participants can implement fair reconstruction secret in four rounds according to the protocol, which reduces the communication complexity of fair and rational secret sharing scheme to a certain extent, and has certain application value.

secret sharing, communication complexity, game theory, bilinear pairing

TP393

A

10.11959/j.issn.2096-109x.2017.00136

李梦慧（1991-），女，河南焦作人，贵州大学硕士生，主要研究方向为理性秘密共享协议效率优化。

田有亮（1982-），男，贵州盘县人，博士，贵州大学教授，主要研究方向为密码与安全协议及算法博弈论。

冯金明（1993-），男，甘肃崆峒人，贵州大学硕士生，主要研究方向为可搜索加密。

2016-10-21；

2016-12-17。通信作者：田有亮，youliangtian@163.com

国家自然科学基金资助项目（No.61363068）；贵州省教育厅科技拔尖人才支持基金资助项目（No.黔教合KY字[2016]060）

Foundation Items: The National Natural Science Foundation of China (No.61363068), The of the Science and Technology Top-notch Talent Support Project of the (No.Guizhou-Education-Contact-KY-Word [2016]060)