二维机织C/SiC复合材料非线性力学行为数值模拟
2017-02-24曾翔龙王奇志
曾翔龙 王奇志
(北京航空航天大学航空科学与工程学院,北京 100191)
(a) 基体
二维机织C/SiC复合材料非线性力学行为数值模拟
曾翔龙 王奇志
(北京航空航天大学航空科学与工程学院,北京 100191)
文 摘 建立了考虑纤维束内部缺陷以及外部基体缺陷的多尺度单胞模型。首先依据电镜扫描图和材料内部单胞的密度,确定了纤维束单胞和复合材料单胞的几何尺寸;然后引入周期性边界条件,利用含缺陷的纤维束单胞模型计算了其初始模量和强度;最后使用由电镜扫描图确定尺寸的复合材料单胞模型,利用上一尺度的材料参数,对复合材料的模量进行了预测;并建立了含损伤纤维束单胞的刚度矩阵,运用基于不同失效模式下损伤状态变量的刚度渐进折减法表征材料积分点损伤,通过数值结果与试验结果的对比,分析了Hashin准则作为判定纤维束起始损伤的适用性,并最终据此给出了单轴载荷作用下受损材料参数的变化情况。分析表明:基于考虑两种缺陷的多尺度模型,使用Hashin准则对C/SiC复合材料单胞进行非线性应力-应变行为数值预报与实验吻合良好。
二维机织,C/SiC复合材料,Hashin准则,细观结构,有限元法
0 引言
C/SiC复合材料具有耐高温、高比强、高比模、抗氧化、抗烧蚀,对裂纹不敏感,不发生灾难性损毁等特点[1]。
国内外对纤维增韧陶瓷基复合材料的力学行为的实验研究颇为重视,然而力学行为模拟计算上大多集中于树脂基复合材料。从T. K.Jacobsen 等[2]得到的C/SiC机织复合材料单轴拉伸应力-应变曲线中可以看出:由于C/SiC复合材料加载过程中裂纹、空洞等缺陷的逐渐扩展,其应力-应变曲线呈现伪塑性,即模量逐渐下降的非线性关系。针对树脂基复合材料,文献[3-5]基于数值方法研究了三维编织复合材料的渐进损伤,并进行了强度预测,然而,陶瓷基复合材料基体模量大、强度低,造成基体率先破坏,且基体呈现脆性,这些与树脂基复合材料呈现不同的特点。陶永强等[6]将2D机织结构简化为0°/90°正交铺层结构,对复合材料在单轴拉伸载荷作用下的渐进损伤进行了分析。然而这一宏观平均方法并不能体现材料细观上缺陷萌生到逐渐扩展的过程,也无法体现不同材料不同的损伤特性。此外,许多模型都未能体现陶瓷基复合材料因制备工艺在纤维束内外基体中形成的缺陷,或是仅仅采用Weibull分布在外部基体中预制一些较小缺陷,这些都与实际结构有很大出入,影响了最后结果的分析。
本文基于考虑纤维束相互挤压的卵圆形纤维束截面单胞模型,引入周期性位移边界条件,采用细观多尺度有限元方法,建立了二维C/SiC平纹机织复合材料的渐进损伤多尺度模型。该模型在两个尺度上对其单胞的力学性能进行考虑:在第一尺度上建立了含预制缺陷的由SiC基体包裹的T300单丝碳纤维各向异性模型,以模拟纤维束的制备缺陷和性能退化;在第二尺度上依据第一尺度均匀化方法得到的力学性能,建立平纹机织C/SiC复合材料单胞模型,结合周期性边界条件,针对不同部分的破坏特点,分别使用Hashin准则和莫尔强度理论,通过ANSYS有限元软件对平纹机织复合材料的渐进损伤过程进行数值模拟。该模型基于纤维束和纯基体相应损伤类型所造成的材料性能退化,模拟了单调拉伸状态下损伤产生、发展的过程,并最终得到了单轴拉伸损伤状况下材料参数的变化规律。
1 能量法原理

(1)
考虑三维各向异性材料的情形,式(1)可表示为:
(2)
和此细观结构相关的应变能可表示为:
(3)
在如表1所示特殊边界条件下,联立(2)、(3)两式可以帮助推断[8]代表性体积单元等效刚度矩阵CH中的系数,并由此可导出材料单胞整体本构方程。同理可得其他矩阵系数。
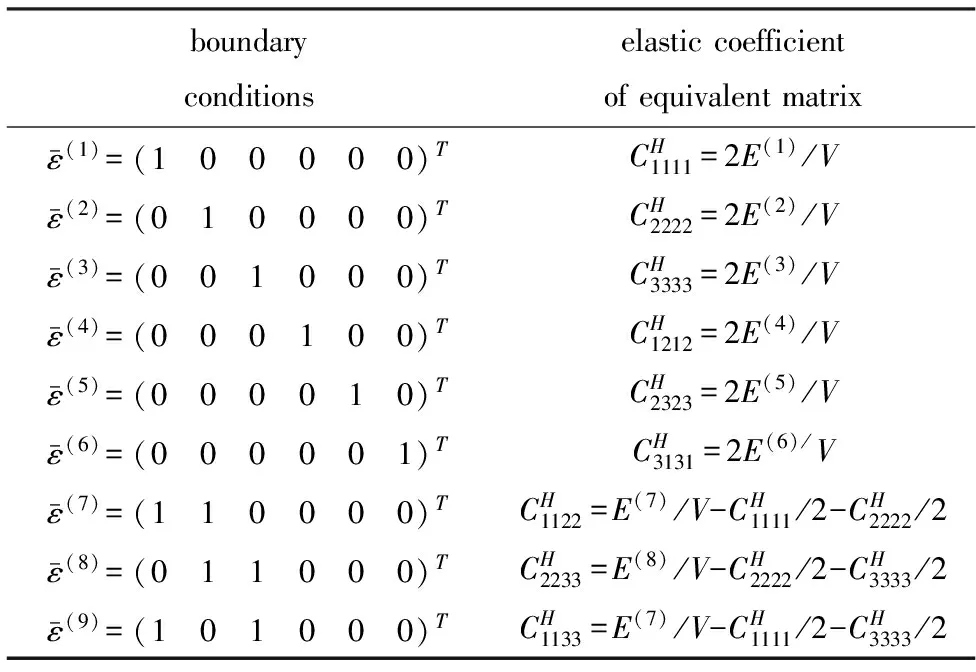
表1 边界条件施加方式
2 纤维束模型的建立
2.1 几何模型的建立
根据图1(a)所示[1]的纤维束内部的电镜扫描结果,碳纤维增韧SiC复合材料(CFCC-SiC)的内部孔隙源自于预制体结构。总体而言,CFCC-SiC内存在两个尺度的孔隙,纤维束间孔隙和纤维束内孔隙(同一纤维束内单丝纤维之间的孔隙)。据此,在纤维束尺度上,可以按照图1(b)所示选取代表性体积元,并建立了如图2(a)所示的纤维束模型,以此进行对纤维束初始材料常数的预测。因此,可以在第一步模型的基础上,于SiC材料中预制一如图2(b)所示的初始缺陷。由此,可以模拟含初始缺陷的纤维束,在单调拉伸过程中,纤维束中的SiC材料逐渐损伤,以至最后失效的过程。
如图2(b)所示,中间为半径R的模拟单丝纤维的圆柱体,外层模拟在纤维束制备过程中分布于纤维束内部的长宽高分别为a、a、H的SiC材料,并在中间预制一直径为d的缺陷,以模拟前文所述纤维束内部孔隙,得到的数值如表2所示。

表2 纤维束单胞几何参数
2.2 有限元模型的建立
依据推算得到表2的几何参数和表3的材料常数,并通过特殊边界条件下的加载,依照前述能量法原理,可确定如表4所示的整体纤维束单胞的材料常数。
表3 有限元模型中各组分材料性质
Tab.3 Material properties used in finite element model
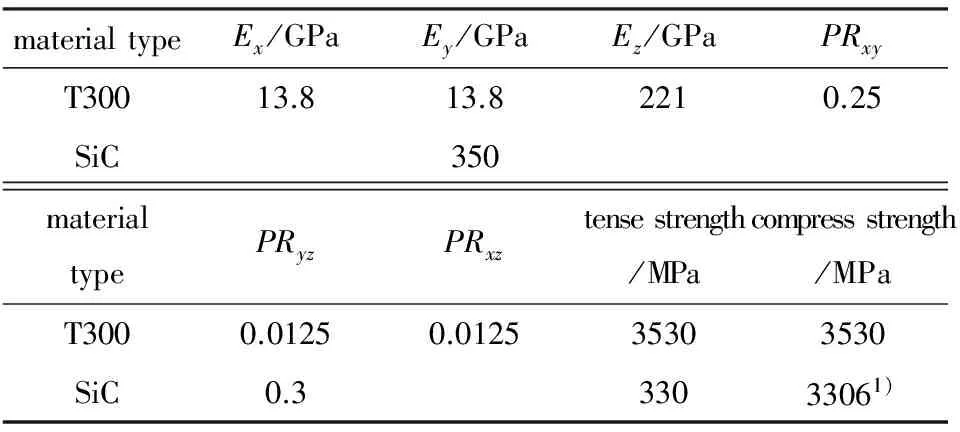
materialtypeEx/GPaEy/GPaEz/GPaPRxyT30013.813.82210.25SiC350materialtypePRyzPRxztensestrength/MPacompressstrength/MPaT3000.01250.012535303530SiC0.333033061)
Explement:1)Superior technical ceramics corp.
表4 纤维束各方向材料性质
Tab.4 Material properties in different direction of finite element model
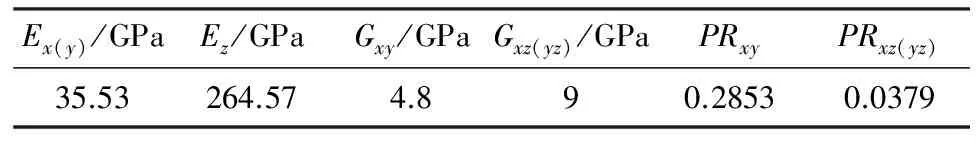
Ex(y)/GPaEz/GPaGxy/GPaGxz(yz)/GPaPRxyPRxz(yz)35.53264.574.890.28530.0379
由于T300单丝碳纤维在轴线方向上具有远大于SiC的拉伸强度,而有较小的刚度,因此在渐进损伤过程中,SiC材料会首先发生破坏。且SiC为高温陶瓷脆性材料,在此采用最大拉应力理论判定其失效。得到的z向(和单丝纤维轴线方向相同)应力-应变结果如图3所示。
从应力-应变曲线中可以看出,与树脂基复合材料破坏主要由C纤维体现不同,单向陶瓷基复合材料纵向破坏呈现两级破坏特点,当应变加载到0.1%左右时,SiC基体开始破坏,应力略微下降,单胞部分损伤,随后由于C纤维的承载应力继续上升。当应变加载到1.6%左右时,C纤维失去承载能力,平均应力开始下降。由此可获得纤维束的起始破坏强度为218 MPa,最终轴向拉伸强度为2 376 MPa。另外施加周期性边界条件[9]可获得,纤维束的横向拉伸强度以及剪切强度,在表5中列出。由表3可以看出C纤维和SiC的压缩强度均较高,因此,本文计算中不考虑纤维束的压缩破坏。
表5 纤维束各方向强度
Tab.5 Strength in different direction of fiber bundle
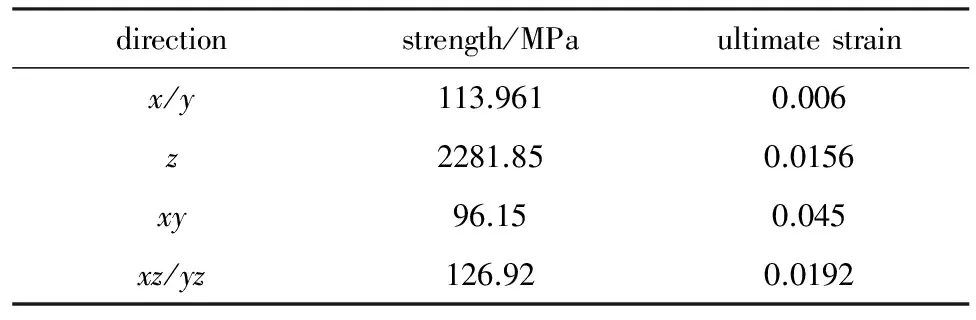
directionstrength/MPaultimatestrainx/y113.9610.006z2281.850.0156xy96.150.045xz/yz126.920.0192
3 C/SiC细观单胞有限元模型
3.1 单胞几何模型
图4为C/SiC复合材料[1]纤维束之间电镜扫描图,明显可见位于板材中间部分由于制作工艺而产生的孔隙,而正是这部分孔隙更容易成为材料破坏的起始位置,有必要对这部分单胞进行建模分析。由此,可按照图5(a)选取代表性体积单元,并建立类似如图5(b)所示的单胞模型,其横截面尺寸见图6。
取复合材料中典型机织结构为一个单胞,如图6所示为机织结构剖面图,假设机织结构中,纤维束截面形状为如图经纱所示的压扁形状,由两段相交圆弧组成,圆弧半径为R1。纤维束形状由两段同心圆弧段组成,两段圆弧半径分别为R1,R1+h/2。模型中相关参数可由电镜照片中经纱纬纱图形测量得到。
3.2 单胞有限元模型
图7(b)为二维C/SiC复合材料单胞有限元模型,浅灰色部分为基体,其余部分为四根交叠的纤维束。其中的纤维束单元为在第一步计算中得到了其初始模量及渐进损伤演化规律的平均化模型,且由于纤维束的分布特点,四根交叠纤维束由八个有不同方向材料参数的部分组成,同时单元坐标系的方向随纤维束的轴线旋转,如图8所示。
为了顺利施加周期性边界条件[9],在有限元网格划分时,必须保证主从面上相应网格节点一一对应,采用网格扫掠的方法来实现,模型主要采用20节点六面体solid 187单元离散,纤维束与纤维束分界面及纤维束与基体分界面均采用共节点方式连接,以保证界面处变形的连续性。
3.3 材料性能退化方案及分析流程
针对C/SiC二维机织复合材料的特点建立了相应的损伤判据。对于纤维束单元,可建立[4]基于损伤状态变量的受损材料的刚度矩阵,如图7所示,其中,Di代表不同损伤模式的损伤度。其定义为:
(4)
式中,Eio代表i方向初始模量,Ei代表i方向实际模量。i=1,2,3分别代表纤维束轴向(L向)、横向(T向)和法向(Z向);i=4,5,6为TZ向、LZ向和LT向。达到损伤准则后,通过设定不同损伤模式的损伤度值,更新该损伤积分点的刚度矩阵,随着载荷增加,在以后增量步模拟中可以达到不同模式的损伤准则,从而继续更新刚度矩阵,实现渐进损伤模拟。对于C/SiC平纹机织复合材料纤维束,由于陶瓷和碳纤维的压缩强度均较大,且纵向弹性模量和横向弹性模量相差较大,因此仅考虑纵向拉剪和横向拉剪两种破坏形式。在此针对纤维束采用Hashin准则[4,12],三维Hashin失效准则具体形式如下。
纤维束轴向拉剪损伤(M1,M2):
(5)
纤维束横向拉剪损伤(M3):
(6)
损伤准则中XT为纤维束轴向拉伸强度,YT为纤维束横向拉伸强度,S12、S23、S12为剪切强度。
当纤维束达到损伤准则后,对各个方向设定不同损伤度,与到达模拟渐进损伤的方法不同,针对基体材料为SiC陶瓷,拉伸与压缩强度相差较大,因此采用莫尔强度准则判定其失效。
(7)
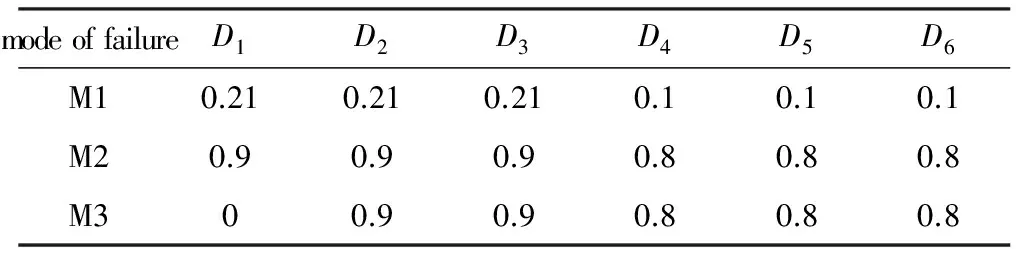
式中,[σt]为拉伸强度,[σc]为压缩强度。基于Hashin准则和莫尔准则的两种材料的刚度退化方案如表6所示。其中,M1代表达到纤维束内部基体破坏强度的拉剪耦合破坏,M2代表达到纤维束整体破坏强度的拉剪耦合破坏。
表6 基于Hashin准则刚度退化方案
Tab.6 Stiffness degradation of Hashin criteria
modeoffailureD1D2D3D4D5D6M10.210.210.210.10.10.1M20.90.90.90.80.80.8M300.90.90.80.80.8
通过ANSYS用户二次开发程序APDL,在材料本构关系中嵌入损伤准则和材料性能退化方案。通过不同损伤准则对组分材料单元进行判断,由此在损伤过程中退化相应的材料性能;利用Newton-Raphson方法计算各增量步单胞中单元应力应变,根据损伤准则更新单元本构矩阵,非线性求解达到收敛,再继续增加载荷步,如此循环完成分析。
(8)
4 数值分析与讨论
4.1 单胞几何尺寸的确定
由于单胞选取的是孔隙率较大的中间部分,且其孔洞由两部分组成,分别分布在纤维束内部的SiC和纤维束外部的基体中。因此,在此依据文献[13]给出的电镜扫描图对纤维束尺寸进行测量如图9所示。其中,文献[13]中给出基体厚度为0.01 mm,其他尺寸依此比例确定,如表8所示。其中g可由几何关系求得,满足关系:
(9)
据此,可反解求得g。
同时,查得C/SiC平纹机织复合材料内部密度[14]ρB为1.56 g/cm3,依据(10)式及C纤维和SiC的密度ρf和ρm,以及假设C纤维的体积分数Vm和复合材料外部致密部分一致的前提下,可推知此时的总体孔隙率Vp:
ρB=ρf×Vf+ρm×Vm+ρp×Vp
(10)
且有:
Vm=Vm,i+Vm,o,Vp=Vp,i+Vp,o
(11)
式中,Vm,i和Vm,o分别为纤维束内部和外部SiC的体积分数;Vp,i和Vp,o分别为纤维束内部和外部孔隙率。
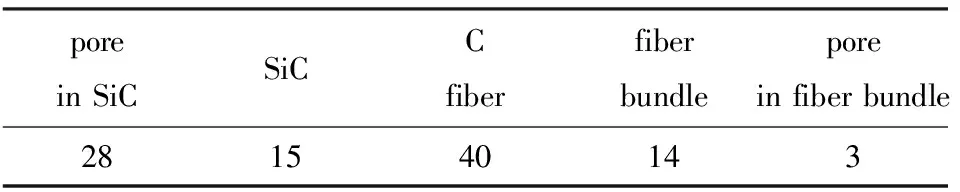
同时依据电镜扫描图获得的复合材料单胞尺寸建立单胞模型,利用CATIA分析工具获取此时外部孔隙率Vp,o,基体和纤维束的体积分数Vm,o和Vf。由式(11),可以最终推知,纤维束内部SiC和孔隙的体积分数Vm,i和Vp,i,如表7所示。复合材料单胞几何参数如表8所示。
表7 复合材料单胞各部分体积分数
Tab.7 Volume fraction of composite unit-cell in different part
vol%
poreinSiCSiCCfiberfiberbundleporeinfiberbundle281540143
表8 复合材料单胞几何参数
Tab.8 Geometrical parameter of composite unit-cell
mm

R1habgt0.71250.30.30.150.07080.01
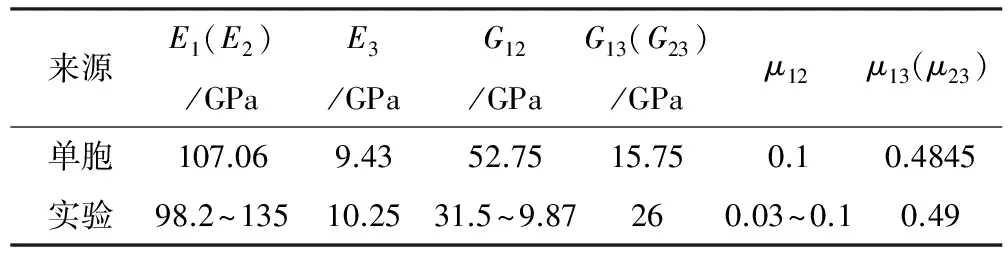
依照前述能量法原理,计算得到C/SiC平纹机织复合材料的等效弹性常数以及文献[1]中查得的材料弹性常数见表9。对比表9中的数据可以看到,计算的面外剪切弹性模量结果略小于实验值。这是由于预制件在CVI过程中,在外部则由于沉积比较充分,填充比较完整。而计算模型只考虑复合材料中的这部分残留孔隙,并未考虑外部完整填充型单胞,导致了计算结果稍小于实验值。
表9 实验数据与计算数据对比
Tab.9 Experimental data compared to calculated data
来源E1(E2)/GPaE3/GPaG12/GPaG13(G23)/GPaμ12μ13(μ23)单胞107.069.4352.7515.750.10.4845实验98.2~13510.2531.5~9.87260.03~0.10.49
4.2 应力-应变曲线
图10分别给出了C/SiC机织复合材料试件在损伤准则下的应力-应变预测曲线和试验曲线。从图10可以看出,二维机织复合材料试件试验曲线和模拟曲线在初始阶段均呈现线性关系。模拟曲线逐步偏离线性是由于局部损伤的发生对宏观应力-应变曲线产生影响,在损伤累积到一定程度以后,曲线开始平缓下降,损伤的逐渐累积将导致材料的最终破坏。
二维机织C/SiC复合材料的力学行为主要由纤维束决定。根据最大拉应力准则判定SiC材料损伤,并引入了纤维束的渐进损伤规律。由于纤维束轴向拉伸强度较大,数值模拟中纤维束损伤的单元不多。在ε=0.06%之前,单胞未发生损伤,应力-应变曲线呈现线性;在ε=0.06%之后,基体单元开始发生损伤,随着损伤单元的增多,应力-应变曲线开始呈现非线性;在ε=0.3%时,继续加载,纤维束各种损伤相对稳定扩展,材料应力-应变曲线逐渐下降,并保持一定的承载能力,材料具有一定的延展性。如图11(a)和11(b)分别为C/SiC平纹机织复合材料纱线和基体的损伤扩展图。由ε=0.06%的纱线损伤图可以看出由于纤维束横向强度较低,因此和纵向纤维交会部分会先产生损伤。这与实验中观察到的结果一致。由图11中ε=0.6%和ε=1.2%可以看出,沿加载方向纤维束受损严重,且中部薄弱处最先破坏。由基体损伤场扩展图可知,基体损伤由中部缺陷开始,并逐渐扩展至整个基体,且在应变较小时损伤较大。

ε=0.06%ε=0.2%ε=0.6%
(a) 基体
4.3 渐进损伤过程中的材料参数变化
C/SiC单胞单轴拉伸受损后,其本构方程可写为:
(12)
表10 单轴应力作用下C/SiC复合材料参数变化
Tab.10 Change of material properties for C/SiC composite under uniaxial load
5 结论
针对平纹机织C/SiC复合材料,利用电镜扫描图,分别建立了内部和外部缺陷模型。同时采取"两步走"的策略,将前一个尺度的计算结果作为后一个尺度性能计算的基础,引入破坏准则,验证了本文所提模型以及计算方法的有效性。
(1)初始阶段C/SiC二维机织复合材料单胞的材料常数与文献中多个实验给出的数据区间一致,证明了所提出的多尺度复合材料单胞的合理性。
(2)应力-应变曲线和实验相差较小以及损伤场的变化趋势与电镜观察一致,证明了基于莫尔强度理论和Hashin准则的分别针对于基体和纤维束的破坏准则的合理性。
(3)可以进一步研究含界面多层陶瓷基复合材料板件中,因制备工艺和技术造成的孔隙大小及其材料组分对复合材料等效性能的影响,进而展开材料性能的优化设计工作。
[1] 张立同. 纤维增韧碳化硅陶瓷复合材料:模拟、表征与设计[M]. 北京:化学工业出版社,2009.
[2] JACOBSEN T K, BRøNDSTED P. Mechanical properties of two plain-woven chemical vapor infiltrated silicon carbide-matrix composites[J]. Journal of the American Ceramic Society, 2001, 84(5): 1043-1051.
[3] 徐焜, 许希武. 三维编织复合材料渐进损伤的非线性数值分析[J]. 力学学报, 2007, 23(3): 398-407.
[4] 张超, 许希武, 毛春见. 三维编织复合材料渐进损伤模拟及强度预测[J]. 复合材料学报, 2011, 28(2): 222-230.
[5] 徐焜, 许希武. 三维五向编织复合材料渐进损伤分析及强度预测[J]. 固体力学学报, 2010, 31(2): 133-141.
[6] 陶永强, 矫桂琼, 王波, 等. 2D 编织陶瓷基复合材料应力-应变行为: 分析预测[J]. 工程力学, 2009(10): 221-227.
[7] XU Y, ZHANG W, BASSIR D. Stress analysis of multi-phase and multi-layer plain weave composite structure using global/local approach[J]. Composite Structures, 2010, 92(5): 1143-1154.
[8] BORKOWSKI L, CHATTOPADHYAY A. Multiscale model of woven ceramic matrix composites considering manufacturing induced damage[J]. Composite Structures, 2015, 126: 62-71.
[9] 张超, 许希武, 严雪. 纺织复合材料细观力学分析的一般性周期性边界条件及其有限元实现[J]. 航空学报, 2013, 34(7):1636-1645.
[10] TABIEI A, YI W. Comparative study of predictive methods for woven fabric composite elastic properties[J]. Composite Structures, 2002, 58(1): 149-164.
[11] BARBERO E J, LONETTI P, SIKKIL K K. Finite element continuum damage modeling of plain weave reinforced composites, Compos. Part B Eng.[J]. Composites Part B-Engineering, 2005, 37(2/3):137-147.
[12] 王新峰. 机织复合材料多尺度渐进损伤研究[D]. 南京航空航天大学, 2007.
[13] 张增光. 2D-C/SiC复合材料的弹性常数预测及失效模式研究[D]. 西北工业大学, 2005.
[14] GUO H B, WANG B, JIA P R, et al. Calculation on tensile strength of notched 2D woven C/SiC composite laminates-considering the nonuniformity of material[C]// 2015 International Conference on Material Science and Applications (icmsa-15),Atlantis Press, 2015.
Numerical Simulation of Nonlinear Mechanics Behavior for 2D Weave Composites
ZENG Xianglong WANG Qizhi
(School of Aeronautical Science and Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100191)
Considering the defect into fiber bundle and outer matrix,a multiscale unit-cell model is establiashed.At first,according to the scanning electron microscope(SEM) photograph and the density into the material,the geometric dimensioning of the unit-cell of fiber bundle and composite is confirmed.Then,introducing into the periodic boundary condition,the initial modulus and strength are calculated by using the fiber bundle unit-cell containing defects.At last,using the composite unit-cell model which confirming geometric dimensioning by SEM photograph,the stiffness is predicted by the material parameters from previous scale.The stiffness matrix of the damaged unit-cell for fiber bundle was established.The damage evolvement method by introducing damage variables of different damage modes were considered as the progressive damage of the material integral points.It was analyzed and discussed by comparing numerical predictions with experimental data.And the damaged material properties under uniaxial load are given at last.The results indicate that numerical simulation of the nonlinear stress-strain behavior based on Hashin failure criteria with various damage modes gives good agreement compared to experimental results.
2D woven,C/SiC composites,Hashin criteria,Mesostructure,FEM method
2016-05-23
曾翔龙,1992年出生,硕士研究生,主要从事复合材料数值模拟方面的研究工作。E-mail:1228624491@qq.com
V45,O341
10.12044/j.issn.1007-2330.2017.01.006
