矩形创新题分类解答

/

矩形创新题分类解答

文/张运虎

矩形是中考的必考内容.近年来，有关矩形问题的创新题很多.为帮助你熟悉新题型，迎接新挑战，现以2016年中考题为例，归纳这类问题的解法，供你学习时参考.

图1

一、开放型

例1（2016年龙东卷）如图1，在平行四边形ABCD中，延长AD到点E，使DE=AD，连接EB，EC，DB，请你添加一个条件，使四边形DBCE是矩形．

解：添加蚁ADB=90°或EB=DC.

二、分割型

例2（2016年益阳卷）将一矩形纸片沿一条直线剪成两个多边形，那么这两个多边形的内角之和不可能是（）

A．360°.B．540°.C．720°.D．900°.

解析：如图2，在以下三种情况中，两个多边形的内角和分别是720°、540°、360°．选D．

图2

三、折叠型

例3（2016年十堰卷）如图3，将矩形纸片ABCD（AD＞AB）折叠，使点C刚好落在线段AD上，且折痕分别与边BC，AD相交，设折叠后点C，D的对应点分别为点G，H，折痕分别与边BC，AD相交于点E，F.

（1）判断四边形CEGF的形状，并证明你的结论；

图3

（2）若AB=3，BC=9，求线段CE的取值范围．

证明：（1）四边形CEGF为菱形.

∵四边形ABCD是矩形，

∴GF∥EC，∴蚁GFE=蚁FEC，

∵图形翻折后点G与点C重合，EF为折线，

∴蚁GEF=蚁FEC，∴蚁GFE=蚁FEG，∴GF=GE，

∵图形翻折后EC与GE完全重合，∴GE=EC，∴GF=EC，

∴四边形CEGF为菱形.

解：（2）如图4，当F与D重合时，CE取最小值，

由（1）可知，四边形CEGD是菱形，∴CE=CD=AB=3；

如图5，当G与A重合时，CE取最大值，

由折叠的性质得AE=CE，∴AE2=AB2+BE2，

即CE2=32+（9-CE）2，∴CE=5，

∴线段CE的取值范围是3≤CE≤5．

图4

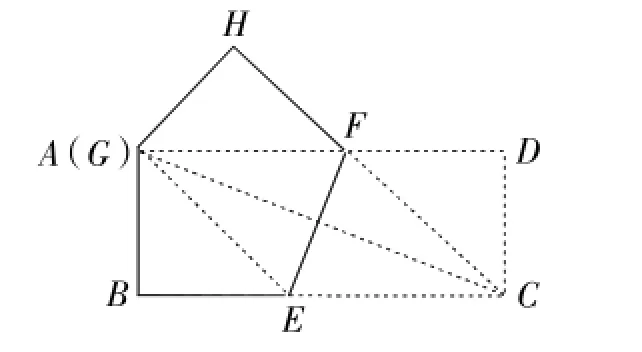
图5

四、说理型

例4（2016年衢州卷）如图6，已知BD是矩形ABCD的对角线．

（1）用直尺和圆规作线段BD的垂直平分线，分别交AD、BC于E、F（保留作图痕迹，不写作法和证明）；

（2）连接BE，DF，判断四边形BEDF的形状，请说明理由.

解：（1）如图6所示，EF为所求直线.

（2）四边形BEDF为菱形.证明如下：

∵EF垂直平分BD，∴BE=DE，蚁DEF=蚁BEF，

∵AD∥BC，∴蚁DEF=蚁BFE，

∴蚁BEF=蚁BFE，∴BE=BF，

∵BF=DF，∴BE=ED=DF=BF，∴四边形BEDF为菱形．

图6

五、阅读型

例5（2016年青岛卷）问题提出：如何将边长为n（n≥5，且n为整数）的正方形分割为一些1×5或2×3的矩形（a×b的矩形是指边长分别为a，b的矩形）？

问题探究：我们先研究解决简单的问题，再把复杂问题转化为已解决的问题．

探究一：如图7，当n=5时，可将正方形分割为五个1×5的矩形；

如图8，当n=6时，可将正方形分割为六个2×3的矩；

如图9，当n=7时，可将正方形分割为五个1×5的矩形和四个2×3的矩形；

如图10，当n=8时，可将正方形分割为八个1×5的矩形和四个2×3的矩形；

如图11，当n=9时，可将正方形分割为九个1×5的矩形和六个2×3的矩形.

图7

图8

图9

图10

图11

探究二：当n=10，11，12，13，14时，分别将正方形按下列方式分割：

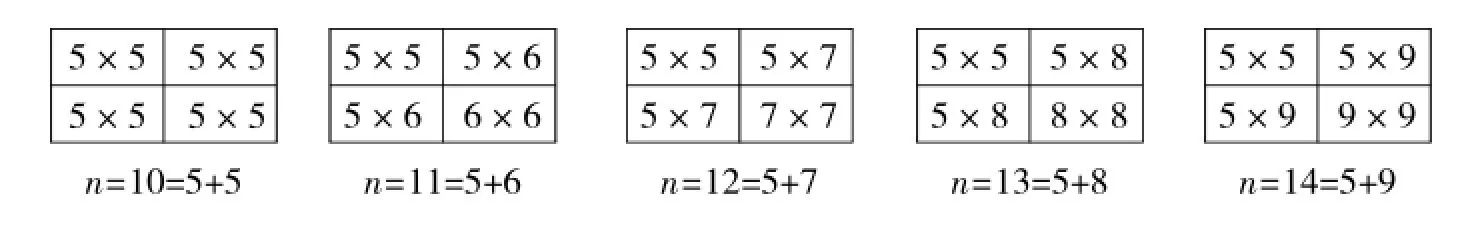
所以，当n=10，11，12，13，14时，均可分割为一个5×5的正方形、一个（n-5）×（n-5）的正方形和两个5×（n-5）的矩形．5×5的正方形和5×（n-5）的矩形均可分割为1×5的矩形，而（n-5）×（n-5）表示边长分别为5，6，7，8，9的正方形，由探究一知可分割为1×5或2×3的矩形．

探究三：当n=15，16，17，18，19时，分别将正方形按下列方式分割：

请按照上面的方法，分别画出边长为18，19的正方形的分割图．

所以，当n=15，16，17，18，19时，均可分割为一个10×10的正方形、一个（n-10）×（n-10）的正方形和两个10×（n-10）的矩形．10×10的正方形和10×（n-10）的矩形均可分割为1×5的矩形，而（n-10）×（n-10）表示边长分别为5，6，7，8，9的正方形，由探究一知可分割为1×5或2×3的矩形．

问题解决：如何将边长为n（n≥5，且n为整数）的正方形分割为一些1×5或2×3的矩形？请画出分割示意图，并加以说明．

实际应用：如何将边长为61的正方形分割为1×5或2×3的矩形？（只需按照探究三的方法画出分割图）

解：探究三：边长为18，19的正方形分割如图12.

问题解决：若5≤n＜10时，如探究一．

若n≥10，设n=5a+b，其中a、b为正整数，5≤b＜10，则分割如图13所示，均可将正方形分割为一个5a×5a的正方形、一个b×b的正方形和两个5a×b的矩形．显然，5a×5a和5a×b均可分割为1×5的矩形，而b×b表示边长分别为5，6，7，8，9的正方形，用探究一的方法可分割为一些1×5或2×3的矩形．

问题解决：边长为61的正方形分割为一些1×5或2×3的矩形，如图14．

图12

图13

图14