基于LM遗传神经网络的短期股价预测
2017-02-22郭建峰
郭建峰,李 玉,安 东
(1.西安邮电大学,陕西 西安 710121;2.英国雷丁大学,雷丁 RG6 6AH)
基于LM遗传神经网络的短期股价预测
郭建峰1,2,李 玉1,安 东1
(1.西安邮电大学,陕西 西安 710121;2.英国雷丁大学,雷丁 RG6 6AH)
随着人工智能的不断发展,BP神经网络作为其中一种重要的技术,被广泛应用在股票预测领域。BP神经网络有很强的非线性逼近能力、自学习自适应等特性,故非常适合解决股价预测中的一些复杂问题。但其在实际的应用过程中还存在一些问题导致其不能很好地进行预测,如网络收敛速度比较慢和容易产生局部最优值等缺点。针对BP神经网络自身存在的这些不足,提出了一种改进的BP神经网络算法。就是通过LM算法改进BP神经网络里的梯度下降法并用遗传算法优化网络参数,即网络的初始权值和阈值,从而提高了网络的收敛速度和搜索全局最优值的能力。用改进后的网络对股票短期价格进行仿真测试,结果表明,改进后的BP神经网络模型有着更快的收敛速度和更高的精确性。
人工智能;BP神经网络;LM算法;遗传算法;股票短期价格预测
0 引 言
随着国内金融业的改革和深入发展,尤其是股票这样一种蕴含潜力和经济利益的金融产品为越来越多的人所关注。股票预测也随之成了一门非常热门的课题。股票投资者在进行股票投资活动时,需要时刻对股票市场进行观测,以便对股价的走势进行预测,从而最大限度地降低风险,增加收益。研究者们通过对股票市场进行长期观察和研究,同时将各种统计学和概率论的方法应用于股票市场[1],从而建立了一些传统的预测模型,如:VAR模型(向量自回归模型)、ARM模型(自回归滑动平均模型)、ARCH模型(自回归条件异方差模型)、多元回归模型、指数平滑模型等[2-4]。这些理论基础比较成熟,并且大多都基于基本的理论,对股票市场的熟悉程度和经验要求较高。其共同的特点都是基于对数据序列的主观模型,然后根据主观的模型和经验进行预测,所以在预测的精度和稳定度方面没有保障,且不具备自适应和自学习的能力。然而,股票市场作为一种复杂系统,受到问题的动态非线性、数据的高噪音、人为操控、政策干预等多种因素的影响,并且各因素相互之间的影响机理也相当复杂[5]。因此,利用传统方法对股票价格进行预测难度很大。
近年来,随着人工智能(Artificial Intelligence,AI)领域研究的不断发展,越来越多的研究者采用人工神经网络建立预测模型对股价进行预测,并取得了较好的预测效果[6]。神经网络由大量的神经元相互连接成为复杂的网络模型,是对人脑的模拟抽象。神经网络具有并行处理、自组织和自调节的能力,是一种高度复杂的非线性系统,很适合处理股价预测中的多因素、非线性动态的不确定性信息处理问题[7]。但是在实际应用过程中,该算法也存在一定的局限性,如易陷入局部极值点、收敛速度慢等问题[8],使得该算法只能对较小规模的问题进行求解,并且得到的极有可能是局部最优解,从而限制了BP(Back Propagation)神经网络算法在股票短期价格预测中的应用。
为了使神经网络能够更好地应用于股票短期价格预测,采用LM(Levenberg-Marquardt)算法优化BP神经网络的梯度下降法,并用遗传算法(Genetic Algorithm,GA)优化BP神经网络的初始权值和阈值。
1 传统BP神经网络
标准的BP神经网络的拓扑结构由三层组成,包括有输入层、隐含层(也称为中间层)和输出层,如图1所示。

图1 三层BP网络结构
同层节点之间不存在相互连接,层与层之间多采用全互联方式,且各层的连接权值可调,输入层和输出层节点根据实际情况而定,隐含层节点数由下式确定:
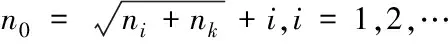
(1)
其中,n0表示隐含层节点数;ni表示输入层节点数;nk表示输出层节点数[9]。
BP网络的学习过程是由工作信号的正向传播和误差信号的反向传播组成。正向传播是由输入层开始逐层计算各层神经元的净输入和输出,误差信号的反向传播是由输出层开始逐层计算各层神经元的输出误差,采用的是梯度下降法,调整各层之间的连接权值使得样本误差减小,使实际输出接近期望值。
BP神经网络具体计算步骤如下:
(2)初始化神经网络。随机产生输入层与隐含层及隐含层与输出层的权重矩阵vij和wjk及隐含层和输出层节点的阈值θi和θk。

(2)
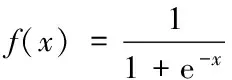
(4)计算输出层的输出:
(3)
(5)计算神经网络的输出误差:
(4)
(6)如果上式得出的误差大于预定误差,则通过梯度下降法修改网络各层的连接权值与阈值,权值修正量分别为:
(5)
(6)
(7)
BP神经网络作为最具有特点的多层前馈人工神经网络,具有较强的线性逼近非线性映射特性,容错性也不错。但由于BP算法本身采用梯度下降法修改权值,极易陷入局部最优值,并且收敛速度较慢。故文中采用LM算法对BP算法进行改进。
2 传统BP神经网络的改进
LM算法属于最优化算法,是使用最广泛的非线性最小二乘算法。它在搜索的过程中同时具有梯度法和牛顿法的优点,使其每次迭代的过程中不再单一地沿着负梯度的方向,而是让误差可沿着上升的方向进行搜索,使目标不易陷入局部最优解[10]。同时通过梯度下降法和高斯牛顿法之间的自适应调整来优化网络权值,提高网络的收敛速度[11]。具体步骤如下:
(1)给定初始值X(0)、误差标准ε。
(2)求目标函数值fi(X(k)),i=1,2,…,m,即fi(X(k))=[f1(X(k)),f2(X(k)),…,fm(X(k))]。

(4)解下列线性方程组,求得梯度搜索方向d(k)。
[J(X(k))TJ(X(k))+μkI]d(k)=-J(X(k))Tf(X(k))
(5)搜索X(k+1)=X(k)+δkd(k)。其中,δk满足:
F(X(k)+δkd(k))=minF(X(k)+δkd(k))
(6)若‖X(k+1)-X(k)‖<ε,则搜索成功;否则转向下一步。
(7)若F(x(k+1)) LM用于修正BP算法的梯度下降法,在与BP神经网络的结合中,其权值的修正公式为: Wij(t+1)=Wij(t)-(JTJ+μI)-1JTe (8) 其中,Wij(t+1)为t+1次迭代时网络的权值;Wij(t)为第t次迭代时网络的权值;J为误差对权值微分的Jacobian矩阵;μ为取值大于零的常量,可以自适应调节,其值很大时,式(8)接近梯度法,很小时,式(8)接近高斯牛顿法;I为单位矩阵;e为误差向量 梯度下降法每次迭代沿着负梯度方向进行,起初误差下降较快,但随着目标逐渐靠近最优值时梯度也接近于零,导致目标函数下降很慢。而牛顿法可在目标靠近最优值时提供一个理想的搜索方向。LM法将二者进行有效结合,大大加快了收敛速度。 遗传算法是一种借鉴生物界自然选择和遗传机制的随机搜索算法,采用群体搜索策略[12]。其思想来源于生物遗传学中适者生存的自然法则,通过群体中个体之间的信息交换,使得本身具有较强的全局搜索能力。将遗传算法与BP神经网络相结合,寻找BP网络的初始权值和阈值,这样能将搜索范围扩至全局,使算法快速高效[13]。遗传算法优化神经网络权值的过程如下: (1)初始化种群的生成:初始化种群大小、遗传代数、交叉概率和变异概率。 (2)编码:对随机产生的连接权值和阈值进行编码,文中采用实数编码方法。 (3)适应度函数计算和选择:以每个样本的误差函数值的倒数作为适应度函数值,选择适应度大的个体进入下一代。 (4)交叉:对从步骤(3)中选出的个体用一定的交叉概率执行部分基因交换产生新个体。 (5)变异:随机挑选对交叉后的个体,让其子代基因产生小概率的变化来保持群体多样性。 (6)算法结束:完成了预定的进化代数或者种群中的最优个体在连续的若干代中没有改进,则输出新种群中适应度最大的个体作为最优解,算法终止。否则返回步骤(3)继续计算。 GA-BP具体实现流程如图2所示。 图2 GA-BP流程图 文中用实数编码对BP神经网络的初始权值和阈值按照一定的顺序进行编码,可以提高解的精准度,且不需要编解码[14]。编码后的总长度即为所有权值和阈值个数之和,即S=R*S1+S1*S2+S1+S2。其中,R为输入层节点个数,S1为隐含层节点个数,S2为输出层节点个数。 编码完成后系统会计算个体适应度,文中将输入输出的相对误差平方和作为适应度函数,即: fitness=1/(SE+1) (9) 其中,SE为误差平方和。 (10) 一般情况下,SE 4.1 仿真条件 为了说明LM-GA改进的BP神经网络对股票预测的效果,分别对BP、LM-BP和GA-LM-BP三种预测模型进行对比实验。 BP神经网络采用三层拓扑结构,输入层神经元个数为15,隐含层神经元个数为7,输出层神经元个数为1。BP神经网络参数设置为:训练次数为3 000,训练目标为1.0e-003,学习率为0.3,动量因子为0.95。遗传算法参数设置为:初始种群规模为40,进化代数为200,选择时的交叉率为0.61,变异率为0.08。 为了减少不同因子之间由于数据大小差异的不同所引起的误差,在学习之前需要对数据进行归一化处理。文中采用premnmx对数据进行处理,处理后数据在[-1,1]范围内均匀分布,函数的一般格式为: [XT,minx,maxx]=premnmx(X) (11) 其中,X为原始输入样本;XT为归一化后的样本;minx和maxx分别为X的最小值和最大值。 4.2 实测股票价格时间序列的预测分析 仿真实验中的数据来自wind金融终端,利用沪深300期货的成交价格数据作为实验数据,采样区间为2014年12月17日-2015年3月6日,频度为每日的1 min高频数据,共5 421个有效样本,其中包括4 000个学习样本和1 421个检测样本。分别采用BP、LM-BP与GA-LM-BP进行预测,结果如图3所示。图中为每隔100 min提取的观测值。 图3 预测结果对比图 沪深300期货的误差统计特性见表1;不同算法的运行过程对比见表2。 表1 沪深300期货的误差统计特性表(单位:点) 表2 不同算法的运行过程对比 从图3、表1和表2中可以看出,GA-LM-BP与其他两种算法相比,在预测的准确性、稳定性及收敛速度方面都有改善,尤其针对传统的BP神经网络,性能得到了较大的提升。 股票市场是一个复杂多变的系统,确立一个有效的系统来预测股价的走向是一个难题。BP神经网络具有良好的线性逼近能力,在股票预测中具有很大的潜力。但是BP神经网络本身存在过拟合现象和易陷入局部最小值的问题,导致其预测效果较差。 针对BP神经网络的上述问题,提出用LM算法进行改进,然后引入遗传算法优化BP神经网络的初始权值和阈值。文中主要使用LM-BP和GA-LM-BP模型,对沪深300期货的成交价格进行了预测。实验结果表明,遗传算法优化的LM-BP模型在迭代时间和次数方面都要优于LM-BP模型。GA-LM-BP收敛速度加快,克服了易陷入局部最优解的缺点,在具体的股价预测分析中的可行性更高。 [1] 刘雁鸣,曾 华.概率统计分布对股票管理分析研究[J].价值工程,2013,32(7):314-315. [2] Nwogugu N.Further critique of GARCH/ARMA/VAR/EVT stochastic-volatility models and related approaches[J].Applied Mathematics and Computation,2006,182(2):1735-1748. [3] Maia A L S,Carvalho F D A T D.Holt's exponential smoothing and neural network models for forecasting interval-valued time series[J].International Journal of Forecasting,2011,27(3):740-759. [4] Xiang C,Fu W M.Predicting the stock market using multiple models[C]//9th international conference oncontrol,automation,robotics and vision.[s.l.]:[s.n.],2006. [5]LeeYJ,ChoHG,WooG.Analysisonstockmarketvolatilitywithcollectivehumanbehaviorsinonlinemessageboard[C]//Internationalconferenceoncomputerandinformationtechnology.[s.l.]:IEEE,2014:482-489. [6]YangL,WangQ.PredictingthestockpricebasedonBPneuralnetworkandbigtransaction[C]//9thinternationalconferenceonfuzzysystemsandknowledgediscovery.Chongqing,Sichuan,China:[s.n.],2012. [7] 任康平.建筑经济管理中神经网络的应用[J].城市建设理论研究,2014(22):3801-3802. [8]LiX,QiB,WangL.AnewimprovedBPneuralnetworkalgorithm[C]//Secondinternationalconferenceonintelligentcomputationtechnologyandautomation.[s.l.]:[s.n.],2009. [9] 张 鹏,崔文利.基于粗糙集优化神经网络结构的启发式算法[J].控制工程,2009,16(1):42-45. [10]BehlingR,FischerA,HerrichM,etal.ALevenberg-Marquardtmethodwithapproximateprojections[J].ComputationalOptimizationandApplications,2014,59(1):5-26. [11] 史步海,朱学峰.LMBP神经网络改进算法的研究[J].控制工程,2008,15(2):164-167. [12] 刘国靖,康 丽,罗长寿.基于遗传算法的主题爬虫策略[J].计算机应用,2007,27:172-174. [13]LiF,LiuC.ApplicationstudyofBPneuralnetworkonstockmarketprediction[C]//Ninthinternationalconferenceonhybridintelligentsystems.[s.l.]:[s.n.],2009:174-178. [14] 张希影.基于遗传算法优化的BP神经网络股票价格预测[D].青岛:青岛科技大学,2014. Prediction for Short-term Stock Price Based on LM-GA-BP Neural Network GUO Jian-feng1,2,LI Yu1,AN Dong1 (1.Xi’an University of Posts & Telecommunications,Xi’an 710121,China; 2.University of Redding,Redding RG6 6AH,UK) With the development of artificial intelligence,BP neural network,as one of the important technology,is widely used in stock prediction.The neural network,which has the capabilities of non-linear approach,self-learning and self-adaption,is very suitable for solving some complex problems in the stock market.But there are many problems in practical applications result in its poor prediction,such as low convergence speed and local minimum.In order to deal with the defects,an improved BP neural network is proposed by using Levenberg-Marquardt (LM) algorithm to improve the gradient descent in BP neural network and Genetic Algorithm (GA) to optimize the network’s initial weights and thresholds.It enhances the convergence speed of the algorithm and the ability to search the global optimization.The model is simulated on short-term stock price prediction and the results indicate that the improved BP model has high convergence speed and accuracy. artificial intelligence;BP (Back Propagation) neural network;LM (Levenberg-Marquardt) algorithm;Genetic Algorithm (GA);short-term stock price prediction 2016-03-14 2016-06-16 时间:2017-01-04 工信部“跨境移动支付与风险管理创新研究课题”(2012R08-2);2015年陕西省软科学重点项目(2015KRA001) 郭建峰(1972-),男,硕士,教授,中组部“千人计划”特聘专家,英国雷丁大学亨利商学院高级研究员,研究方向为计算金融;李 玉(1992-),女,硕士研究生,研究方向为计算金融。 http://www.cnki.net/kcms/detail/61.1450.TP.20170104.1102.082.html TP301.6 A 1673-629X(2017)01-0152-04 10.3969/j.issn.1673-629X.2017.01.0343 LM-BP神经网络的优化

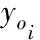
4 实验结果分析

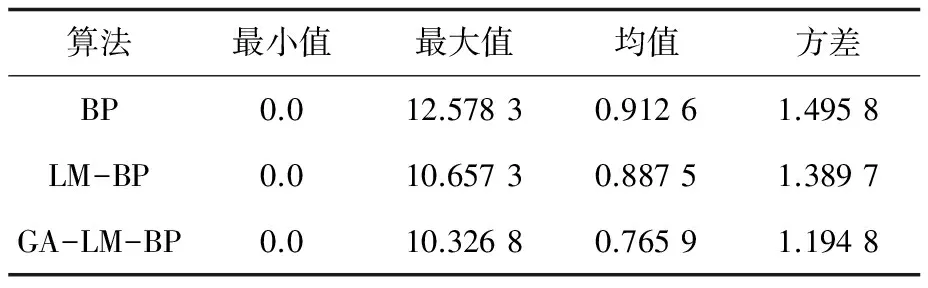

5 结束语
