一种基于禁忌策略的混合优化算法
2017-02-22印溪,许斌,亓晋
印 溪,许 斌,亓 晋
(1.南京邮电大学 自动化学院,江苏 南京 210003; 2.南京邮电大学 物联网学院,江苏 南京 210003)
一种基于禁忌策略的混合优化算法
印 溪1,许 斌2,亓 晋2
(1.南京邮电大学 自动化学院,江苏 南京 210003; 2.南京邮电大学 物联网学院,江苏 南京 210003)
为了提升综合学习粒子群算法(Comprehensive Learning Particle Swarm Optimization,CLPSO)的后期收敛能力,提出一种基于禁忌策略的混合优化算法,记为CLPSO+Tabu(CMA-ES)。算法以禁忌搜索算法为后续搜索操作,对综合学习粒子群算法进行改进。同时将协方差矩阵自适应进化策略(Covariance Matrix Adaptation Evolution Strategy,CMA-ES)引入禁忌搜索算法,以高斯分布为基础,以CMA-ES策略引导邻域结构的分布,构造新型自适应邻域结构,指导禁忌搜索算法中候选解的选取,从而解决综合学习粒子群算法在收敛精度低的问题,极大改善了求解效果。针对26个标准测试函数的实验结果表明,与CLPSO相比,CLPSO+Tabu(CMA-ES)算法在绝大多数函数上具有更好的收敛效果。针对其中6个优化问题,CLPSO+Tabu(CMA-ES)更是有至少一个数量级的改进。
综合学习粒子群算法;禁忌搜索;高斯分布;参数自适应;协方差矩阵自适应进化策略
0 引 言
D维无约束优化问题可以表达为:minf(x),x∈Rn。对于非线性、高维、非凸、病态等函数优化问题,传统算法通常不能很好地利用目标函数的梯度信息或者次梯度信息进行优化。而群智能优化算法[1]是通过转移概率在解空间内进行选择和搜索,故而具有全局搜索能力强、收敛快、搜索效率高、鲁棒性好等优点,为解决管理科学、计算机科学、控制工程等领域的优化问题提供了新的求解途径[2]。目前群智能优化算法已成为最优化方法中的研究热点[3]。
群智能优化算法是一种通过模拟动物集体行为来求解优化问题的智能算法。与传统算法相比,该算法的实现较简单,对要解决的问题是否连续以及问题的规模均无要求,并且具有广泛的适应性和鲁棒性[1]。
综合学习粒子群算法自提出以来,很多专家在增强CLPSO性能以及扩展CLPSO应用等方面进行了相应的研究与工作。Liang和Suganthan提出了自适应CLPSO,其中,粒子的学习概率随着过去几代取得的最大改进的差值而自适应改变,同时将历史改进方向加入到粒子速度的更新中。HasanzadehM在CLPSO的基础上引入自动学习机,对CLPSO的算法性能、鲁棒性以及收敛速度都有提升。
虽然有了众多的改进和融合,CLPSO的性能也得到了相应提升,但目前其只在解决一部分多峰问题上有较好的效果[4],而在单峰问题以及一部分多峰问题上效果较差,算法后期的收敛速度慢,求解精度不足[5]。
基于综合学习粒子群算法,文中提出一种融入禁忌算法的搜索方法。算法中以综合学习粒子群算法作为全局搜索算法,以禁忌算法作为局部搜索算法。由于禁忌搜索需要较好的初始解,才能得到较好的局部搜索能力,因此,以综合学习粒子群算法的结果作为禁忌搜索的初始解,以CMA-ES策略控制高斯分布的参数变化,以高斯分布作为自适应邻域结构,选取候选解。针对26个特性各异的函数的实验表明,与CLPSO相比,文中算法在解决函数优化问题上有一定的优势,尤其是在优化旋转函数上较显著。
1 相关工作
1.1 CLPSO
Liang J J[6]基于经典PSO提出了基于综合学习策略粒子群优化算法-CLPSO。CLPSO使用一种新颖的学习方法,利用所有其他的粒子历史最优信息来更新粒子的速度,使得算法中的粒子多样性得以保持,从而一定程度上避免了过早收敛。
CLPSO的速度和位置更新公式为:
(1)

(2)

每个粒子均产生[0,1]内的均匀随机数,若产生的随机数大于设定的学习概率Pc,则设定学习对象为pbest,即粒子本身的历史最优位置;若产生的随机数小于设定的学习概率,则按锦标赛选择策略(tournamentselectionprocedure)从种群内随机选取的两个个体中选出较优的历史最优位置作为学习对象。
为上述学习对象选择过程中设定一个更新间隔代数(refreshinggap)m,即粒子的适应度值经过m次迭代都不再改进后,重新分配学习对象,否则,保持上次选择的学习对象不变。该策略可以使粒子向优秀的对象学习,而不会在较差的对象上浪费时间[7]。
CLPSO的每个粒子的每一维都可以随机地向自身或其他粒子学习。该策略使得粒子群中的粒子保持了较好的多样性,从而避免了过早收敛的现象。其在解决多峰问题上具有较好的性能,但在单峰问题上效果却不够好。而现实中,问题的适应度景观形态通常未知,将CLPSO与局部搜索算法结合起来就能有效解决单峰问题[8]。
1.2 Tabu
禁忌搜索算法[9](Tabu Search)是一种现代启发式算法,由美国科罗拉多大学教授Fred Glover提出,是一种用来跳出局部最优解的搜索方法。
简单TS算法的基本思想:首先,给定问题的一个初始解,同时,选择一种邻域结构。然后,在初始解的邻域中随机确定一些候选解。此时,如果最优候选解对应的适应度值优于“best so far”状态,则用该最优候选解代替初始解和“best so far”状态,同时将其加入禁忌表,并修改禁忌表中对象的禁忌时间;如果最优候选解对应的适应度值并不优于“best so far”状态,则新的初始解在候选解中的非禁忌的最优状态中选出,即忽略其与初始解的优劣关系,并将其加入禁忌表,同时修改禁忌表中对象的禁忌时间。如上述般重复迭代搜索过程,当满足停止准则时,才可停止。
文中应用的藐视准则是基于适应度值准则中的全局形式。采用的终止准则:给定每次运行后总循环的次数,即最大迭代步数。
2 算法描述
2.1 邻域结构
禁忌搜索的性能基本依赖于所选取的邻域结构和所给定的初始解。文中的初始解由CLPSO提供。选取不同的邻域结构将得到不同的禁忌算法,而邻域结构的设计通常与问题有关。
采用高斯分布(Gaussian distribution),又称正态分布(Normal distribution),高斯分布有两个参数:位置参数μ,意味着高斯曲线的中心位置;尺度参数σ,意味着高斯曲线的陡峭程度。
高斯分布的概率密度函数为:
(3)
3σ原则意味着,正态曲线下变量取值在(μ-3σ,μ+3σ)中的概率为99.7%。
文中Tabu算法将初始解设为位置参数μ,使得候选解在初始解的3σ范围内,且离初始解越近,取到的机率就越大,即以初始解为中心,在其周边3σ范围内进行候选解的选取。σ的大小意味着候选解可能的取值范围。为控制σ的大小,引入协方差矩阵自适应进化策略,随着进化代数的推进,自适应地改变σ的取值,从而影响候选解选取的范围。
2.2 CMA-ES
协方差矩阵自适应进化策略[10](Covariance Matrix Adaptation Evolution Strategy,CMA-ES)由Hansen和Ostermeier提出,是一种新型的基于生物进化的优化算法。该进化策略适用于解决随机的、不可导的非线性或非凸连续优化问题。进化方法大多基于生物进化,重复作用的变异(包括重组和突变)以及选择。在CMA-ES中,新的候选解是根据多元正态分布来选择的。重组相当于为分布选择一个新的平均值。突变则相当于增加了一个随机变量,增加了一个平均值为0的扰动。协方差矩阵记录的是两个变量的相关性,而CMA是更新这个协方差矩阵的一种方法。由于CMA-ES具有旋转不变性,其在解决旋转函数和病态函数时特别有效。CMA-ES策略的核心是动态自适应地调整变量建的协方差矩阵,使得种群逐步收敛于全局最优解。
文中主要引入CMA-ES中的自适应迭代步长的方法,从而自适应地控制邻域解的分布范围以及取值概率,既保持了邻域解的多样性,同时也确保了解的精确度。
σ的步长控制函数为:
(4)
其中,pσ为进化路径,其更新公式为:
(5)
Cg是第g代的协方差矩阵,其更新公式为:

(6)
协方差矩阵自适应进化策略结合了进化策略方法的全局性和协方差矩阵的可引导性,对于解决非凸非线性优化函数问题有非常好的适应能力。
2.3 基于CMA-ES的CLPSO算法
为了进一步增强CLPSO的局部搜索能力,提高解精度,引入禁忌搜索算法。以CMA-ES策略引导高斯邻域结构的变化,自适应地产生较好的邻域解,从而获得更精确的解。
根据上述策略,文中提出CLPSO+Tabu(CMA-ES),其算法的框架如下:
第一步:初始化。
(1)对种群中每个个体的位置进行随机初始化;
(2)计算初始化后个体的适应度值,将最优值存储于pbestval,将最优解存储于pbest;
(3)对种群中每个个体的速度进行随机初始化。
第二步:用锦标赛的方式挑选学习对象。
在种群中随机挑选两个粒子进行比赛,根据两个粒子pbest的适应度值的大小判断输赢,适应度值优的一方获胜。若其值相同,则随机选取。利用较好的那个粒子的pbest作为更新的标本,如果一个粒子的所有标本都是自身pbest,就随机抽取其中一维来学习其他粒子的pbest。
第三步:更新。
依据式(1)和(2)更新粒子的位置与速度,从新的粒子中选出最优解,更新pbest和pbestval。
第四步:停止CLPSO。
当函数评估次数达到预设值,停止CLPSO的进化,将最后一代的最优解作为初始解。
第五步:用禁忌搜索来更新粒子作为下一代种群。
(1)在CLPSO产生的初始解的邻域中寻找候选解。
①更新协方差矩阵Cg,更新进化路径pσ。
②计算邻域大小。
(2)选出候选解中最优解作为“bestsofar”状态。
(3)根据候选解是否满足藐视规则,更新初始解、禁忌表、“bestsofar”状态。
(4)判断候选解对应的各对象的禁忌属性,更新初始解和禁忌表。
第六步:停止禁忌搜索。
当“bestsofar”状态连续50次未进化,则停止搜索,输出最后一代的“bestsofar”状态。
第七步:迭代次数加1,跳回第一步重新开始,当达到最大迭代次数停止进化并输出最优的“bestsofar”状态。
经过实验验证,该算法在优化旋转函数上优势显著,由于禁忌算法的加入,CLPSO+Tabu(CMA-ES)算法在单峰问题中较经典CLPSO效果更优秀,而在非离散问题和病态问题上,效果也有一定程度的改进。
3 实 验
3.1 测试函数
利用26个具有不同特性的测试函数来对算法进行测试,测试函数详见文献[11]。
其中,Ackley函数是由指数函数加适度放大的余弦波经过调制得到的多峰连续型实验函数,存在多个局部极小值点;Sphere函数是单峰二次函数;Rosenbrock函数,又称香蕉函数,非凸,为病态函数;Rastrigin函数是多峰函数,存在大量局部极小点;Griewank函数是多峰函数,存在大量局部极小点;Schwefel函数是一种典型的欺骗问题,具有许多虚假的局部最小值,算法极易陷入局部最优;diff pow为连续单峰函数;Quadric是一种径向基函数,取值仅仅依赖于离原点距离的实值函数。
3.2 参数取值
3.2.1 禁忌表及禁忌长度
在不考虑藐视准则的情况下,禁忌长度是禁忌对象不能被选取的最大次数,只有当其禁忌时间为0时才可以被解禁。禁忌长度小,则相应算法的计算量和存储量小;但是,禁忌长度过小,将造成循环搜索。文中禁忌长度取为7[12]。
3.2.2 学习概率Pc
学习概率的设置影响了每个粒子的学习能力。不同的学习概率对算法的探测和搜索能力有很大影响。研究[13]表明,学习概率为[14]:
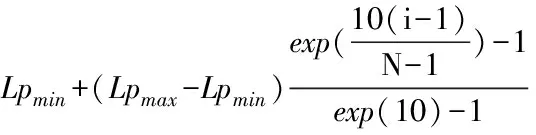
(7)
其中,Lpmax和Lpmin分别对应学习概率的最大值和最小值,根据经验,Lpmax=0.5,Lpmin=0.05;N为种群的粒子数。
3.2.3 惯性权重w
已有的研究工作[15]表明,较大的惯性权值有利于搜索时跳出局部极值点,而较小的惯性权值有利于算法收敛和提高搜索精度。因此提出惯性权重自适应动态调整的策略,在算法初始阶段,使惯性权值较大,随着算法的运行,其值又逐渐减小,即随着CLPSO的进化,惯性权重应线性减小,从而达到算法探测能力和搜索能力的平衡。通常,惯性权重的值保持在0.1~0.9之间。惯性权重由式(8)表示。
(8)
其中,wmax是惯性权重的最大值;wmin是惯性权重的最小值。文中wmax=0.9,wmin=0.4。
3.2.4 更新间隔代数m
为学习对象选择过程设定一个更新间隔代数(refreshinggap)m,即粒子的适应度值经过m次迭代都不再改进后,重新分配学习对象,否则,保持上次选择的学习对象不变。研究[16]表明,m通常取7,效果较好。故文中更新间隔代数取7。
3.3 实验结果及分析
实验设置测试函数的维数为30,设置最大函数评估次数为900 000,设置综合学习粒子群算法中的粒子数为60,禁忌搜索中邻域解的个数为100,禁忌表长度为60。对于所有的函数,每种算法均独立运行10次。
表1给出了CLPSO+Tabu(CMA-ES)、CLPSO在26个测试函数上10次运行的平均最优值及其标准差、适应度函数评价次数及其标准差。

表1 运行结果
部分函数的收敛过程如图1所示。
由表1可以看出CLPSO+Tabu(CMA-ES)算法在26个函数上的最优值大多比经典CLPSO算法的结果更优。而在不同的函数上,该算法的优势大小也不同。CLPSO+Tabu(CMA-ES)相比于经典CLPSO在函数F2、F5、F15、F17、F18、F19上有至少一个数量级的改进,在12个函数上有改进。由上述数据可以看出,CLPSO+Tabu(CMA-ES)算法在优化旋转函数上的优势较经典CLPSO更为显著。
函数F1到F5是单峰问题。CLPSO+Tabu(CMA-ES)算法在函数F2、F5上比CLPSO算法有更优异的表现。函数F6到F11是离散多峰问题,局部最优值随着维数的增大而增大。如表1所示,在这些函数中,CLPSO+Tabu(CMA-ES)算法的性能仅与经典CLPSO算法相持平。函数F12到F14是Rosenbrock函数和Rastrigin函数所衍射的函数问题。文中算法在这三个函数上只有些许改进甚至没有改进。函数F15是由F2产生的问题,系统的高斯噪声使得寻找全局最优值变得困难。在这个问题上,CLPSO+Tabu(CMA-ES)算法比经典CLPSO算法改进了至少一个数量级。函数F16到F26测试了算法解决非离散和病态问题的能力。F23、F24、F25是多峰问题。
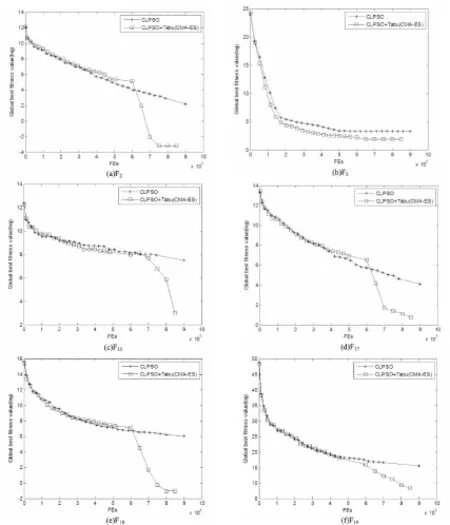
图1 CLPSO+Tabu(CMA-ES)和CLPSO在函数F2、F5、F15、F17、F18、F19上的收敛特性
文中算法由于采用了自适应的高斯分布邻域结构,保持了解的多样性和精确度,在大部分函数上均有改进,而改进的大多数为旋转问题。因此,CLPSO+Tabu(CMA-ES)算法具有解决好旋转问题、非离散问题和病态问题的能力。
4 结束语
文中以禁忌搜索算法为综合学习粒子群算法的后续局部搜索操作,弥补了综合学习粒子群算法后期收敛能力弱的缺点。禁忌搜索算法的性能和邻域结构以及禁忌表密切相关,针对禁忌搜索算法的邻域结构进行改进,以高斯分布作为邻域结构,并利用CMA-ES策略控制邻域结构的步长。通过在26个不同特性的函数上的实验,与经典CLPSO算法相比,文中算法求解精度相对提高,很好地解决了综合学习粒子群算法在后期收敛难的问题。
[1] 李雪梅,张素琴.基于仿生理论的几种优化算法综述[J].计算机应用研究,2009,26(6):2032-2034.
[2] 魏连伟.基于人工智能技术的地下水系统参数识别研究[D].天津:天津大学,2003.
[3] 黄婉平.自适应粒子群优化算法及其应用研究[D].杭州:浙江大学,2006.
[4] 许 君,鲁海燕,石桂娟.限制速度粒子群优化和自适应速度粒子群优化在无约束优化问题中的应用[J].计算机应用,2015,35(3):668-674.
[5]KennedyJ.Particleswarmoptimization[M]//Encyclopediaofmachinelearning.Boston,MA:Springer,2010:760-766.
[6]LiangJJ,QinAK,SuganthanPN,etal.Comprehensivelearningparticleswarmoptimizerforglobaloptimizationofmultimodalfunctions[J].IEEETransactionsonEvolutionaryComputation,2006,10(3):281-295.
[7]LynnN,SuganthanPN.Comprehensivelearningparticleswa-rmoptimizerwithguidancevectorselection[C]//Proceedingsofthe2013IEEEsymposiumonswarmintelligence.Singapore:IEEE,2013:80-84.
[8] 许 骏,许晓东.一种群体智能融合算法及其在应急设施选址的应用[J].计算机工程与科学,2014,36(4):667-673.
[9]DewerraD,HertzA.Tabusearchtechnique-atutorialandanapplicationtoneuralnetworks[J].OperationsResearch,1989,11(3):131-141.
[10]OstermeierH.Adaptingarbitrarynormalmutationdistributionsinevolutionstrategies:thecovariancematrixadaptation[C]//Proceedingsofthe1996IEEEinternationalconferenceonevolutionarycomputation.Nagoya:IEEE,1996:312-317.
[11]WangY,LiB,WeiseT,etal.Self-adaptivelearningbasedparticleswarmoptimization[J].InformationSciences,2011,181(20):4515-4538.
[12] 潘全科,朱剑英.一类解决JobShop问题的禁忌搜索算法[J].中国机械工程,2006,17(5):536-539.
[13]LiangJJ,QinAK,SuganthanPN,etal.Evaluationofcomprehensivelearningparticleswarmoptimizer[J].LectureNotesinComputerScience,2004,3316:230-235.
[14] 蔡昭权,黄 翰.自适应变异综合学习粒子群优化算法[J].计算机工程,2009,35(7):170-171.
[15] 刘关俊.基于粒子群算法的移动机器人路径规划研究[D].长沙:中南大学,2007.
[16]LiangJJ,SuganthanPN.Adaptivecomprehensivelearningparticleswarmoptimizerwithhistorylearning[C]//Simulatedevolutionandlearning.Berlin:Springer-Verlag,2006:213-220.
A Hybrid Optimization Algorithm Based on Tabu Strategy
YIN Xi1,XU Bin2,QI Jin2
(1.College of Automation,Nanjing University of Posts and Telecommunications,Nanjing 210003,China; 2.College of Things of Internet,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)
In order to enhance the convergence ability of the Comprehensive Learning Particle Swarm Optimization (CLPSO) in the later stage,a hybrid optimization algorithm based on Tabu strategy is proposed and it is denoted by CLPSO+Tabu (CMA-ES).It improves CLPSO by taking Tabu strategy as the subsequent search operation.Moreover,the Covariance Matrix Adaptation Evolution Strategy (CMA-ES) is introduced to the Tabu algorithm,which is based on Gaussian distribution.The CMA-ES guides the distribution of neighborhood structure to construct new adaptive neighborhood structure,then guides the selection of candidate solution,which can solve the problem of low convergence rate and improve the effect.The experimental result based on the 26 standard test functions shows that CLPSO+Tabu(CMA-ES) has better convergence effect than CLPSO.And it has improvement of at least one order of magnitude in six functions.
comprehensive learning particle swarm optimization;Tabu strategy;Gaussian distribution;parameter adaption;CMA-ES
2015-12-21
2016-05-12
时间:2017-01-10
国家自然科学基金资助项目(61401225);中国博士后科学基金资助项目(2015M571790)
印 溪(1992-),女,硕士研究生,研究方向为智能计算与智能系统;许 斌,博士,讲师,研究方向为智能计算、云制造服务组合;亓晋,博士,讲师,研究方向为新一代网络、大数据管理与智能计算、云计算。
http://www.cnki.net/kcms/detail/61.1450.TP.20170110.0941.012.html
TP301.6
A
1673-629X(2017)02-0046-05
10.3969/j.issn.1673-629X.2017.02.011
