基于海量数据的二维凸包快速生成算法
2017-02-22蔺东杰凌广明
马 骏,蔺东杰,凌广明
(1.河南大学 计算机与信息工程学院,河南 开封 475004; 2.河南大学 软件学院,河南 开封 475004)
基于海量数据的二维凸包快速生成算法
马 骏1,蔺东杰1,凌广明2
(1.河南大学 计算机与信息工程学院,河南 开封 475004; 2.河南大学 软件学院,河南 开封 475004)
凸包算法是计算机几何的基本问题之一,在很多领域应用广泛。传统的凸包生成算法在处理大容量数据时,表现出的时间复杂度相对较高而且凸包生成速率较低,已经不能满足实际海量数据的需求。为解决这一问题,提出了一种面对海量数据的快速凸包生成算法。该算法通过对散乱点集分区、一遍扫描排序,确定散乱点集边界,快速处理边界点集中处于共线的点等一系列预处理操作,快速排除凸包内部的点,缩小了问题规模,避免了对不在凸包上的点集的扫描处理,明显地缩短了凸包的求取时间,可保证最小凸包的快速生成。该算法极其简单,时间复杂度较低,理论上可达到o(nlogn),有利于凸包生成速度的提高。与传统算法进行了同步对比实验,结果表明,该算法运行有效性较好,且具有较好的应用前景。
凸包;海量;平面点集;预处理;排序;快速
0 引 言
凸包是指包含平面点集内所有点并且顶点属于平面点集的最小简单凸多边形。它作为计算几何的基本单元之一,广泛应用于图像处理、模式识别、地理信息系统、人工智能等领域。对于凸包的研究,一直是计算
几何领域研究的热点之一[1]。
自20世纪60年代末,贝尔实验室要求求解10 000个点的凸包。此后众多学者提出了大量经典的算法和改良算法[2]。
1970年,Chand和Kapur提出了任意维空间的gif-wrapping算法。该算法通过不断查找使相邻平面内角最大的超平面直到平面集合封闭来确定点集的凸包。该算法的时间复杂度为o(n2),其中n为点集中点的数量[3]。
1972年,Graham提出了时间复杂度低于o(n2)的算法,该算法的时间复杂度为o(nlogn);1978年,Anderson重新评估Graham算法,简化计算来确定连续三个点中第二个点是否为凸点。之后Koplowitz和Joup、Atwah、Baker分别在1978年、1995年和2002年在Graham算法的基础上提出了快速二维平面点集凸包算法[4]。1973年,Jarvis提出了包含点缺失检测的凸包算法,并且证明当平面上点数相对较少时算法有效[5]。
1972年,Sklansky提出了具有线性时间复杂度的简单多边形凸包算法,但遗憾的是1978年Bykat发现该算法有可能产生自交的多边形并举出了反例,同年提出了一种新的具有线性时间复杂度的简单多边形凸包算法,该算法很快也被推翻[6]。1989年,台湾大学的陈诚林在Sklansky算法基础上提出的算法,较为简单有效[7],但浙江大学的吴中海博士于1997年发表文章指出了其中的细节错误并提出了改进算法[8]。
目前提出的算法中除了卷包囊算法、Gramham法、QuickHull法、Incremental法之外,还有BruteForce算法[9]。这些经典的凸包生成算法,其结构相对简单,因此在各个领域中应用广泛。但随着数据量的不断增加,这些算法已经不能满足应用的需求。当平面点集数量达到106时,这些算法付出的时间和空间代价过大[10]。
为解决这一问题,文中提出基于海量数据的二维凸包快速生成算法。该算法在Gramham算法的基础上通过分区、排序等预处理操作快速去除肯定不在凸包上的点集,同时对边界点集进行排序等操作,缩小问题规模,快速生成凸包,并与传统算法进行测试对比。结果表明,该算法理论时间复杂度和空间复杂度相对较低。
1 凸包及其相关概念
定义1:设点集S⊆Rn,S中任意有限个点的所有凸组合所构成的集合称为S的凸包,记为H(S),即
H(S)=
点集S的凸包H(S)也可以描述为包含点集S的所有凸集或半空间的公共交集。它是包含点集S的最小凸集[11]。
在Ed空间上的点集S的凸包是由S中至多d+1个点的所有凸组合的集合。因此,平面点集的凸包是点集中至多3个点的凸组合的集合,任意3个点的凸组合的集合构成一个三角形,因而平面点集的凸包可以看成是点集中任意3个点的凸组合的集合确定的三角形的并集[12]。

S(A,B,C)=(xb-xa)×(yc-yb)-(xc-xb)×(yb-ya)
根据S的正负号来判断顶点B的凹凸性,如图1所示。
(1)如果S>0,B为凸点;
(2)如果S<0,B为凹点;
(3)如果S=0,B为平坦点。

图1 点的凹凸性判断
定义3:给定平面内任意直线AB两端点坐标,A(xA,yA),B(xB,yB)和一点P(xP,yP),判断点P与直线AB的位置关系。
设直线AB的方程是:
将点P代入到上述方程中得:
F=xA(yB-yP)-yA(xB-xP)+(xByP-xByB)
点P与直线AB的位置关系如图2所示。
(1)F>0时表示点在直线的上方;
(2)F<0时表示点在直线的下方;
(3)F=0时表示点在直线上。
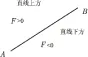
图2 P与直线AB的位置关系
2 传统算法思想
传统的凸包算法是一种比较常用的算法,其算法思想如下:
以上方点集最小凸包求取为例,根据上述最小凸包求取的思想可知,线段PminPmax上方点集的最小凸包必包含点段PminPmax的两端点,因此如果线段PminPmax上方无任何数据点,则上方最小凸包由点Pmin和Pmax构成。如果线段PminPmax上方数据点较多,则上凸包求取步骤如下:
(1)设线段PminPmax上方数据点中距离最远的点为Pl,连接线段PminPl和线段PlPmax。
(2)分别找到线段PminPl和PlPmax上方点集中距离最远的点,如果PminPl和PlPmax上方均无数据点,则上凸包由点Pmin、Pl和Pmax构成。
循环执行步骤(1)和步骤(2)直到各个线段上方均无数据点为止。上凸包求取示意图如图3所示。

图3 凸包求取示意图
根据算法的基本思想可知,在凸包的求取过程中每确定一个凸包顶点,就要判断线段之外是否还有其他数据点,这样就需要遍历点集中的数据点两次。当数据点个数和顶点个数均较大时,判断次数将是数量级级别的增长,如果面对海量数据,其凸包求取速度难以想象,直接影响系统的运行效率。因此传统凸包算法已不能满足具体现实需求[15]。
3 文中算法思想
3.1 点集预处理


图4 点集的子集划分
以如图5(a)所示的点集为例,简述平面点集的预处理:

图5 点集预处理
(1)从点集中确定极值点,即点A、B、C、D,如图5(b)所示。
(2)根据点与直线的位置关系函数F,将散乱点集分为五个区域,并将点集V删除,如图5(c)所示。
(3)将点集V1、V2中的点按照x坐标值从小到大排序,当x坐标值相等时,选择y坐标值最小的点,将y坐标值相对较大的点删除;同理将点集V3、V4中的点按照x坐标值从小到大进行排序,当x坐标值相等时,选择y坐标值最小的点,将y坐标值相对较大的点删除,如图5(d)所示。
(4)从点A出发,将点A、子集V1中的点、点D、子集V2中的点、点B、子集V4中的点、点C、子集V3中的点按照逆时针方向连接,这样凸包边界就确定了。分界线以上的点按照x坐标从大到小连接,分界线以下的点按照x坐标从小到大连接,如图5(e)所示。
经过第二步的处理已经删除的大部分不在凸包上的点,再加上第三步的处理,不仅进一步删除不在凸包上的点,同时对凸包边界上的点进行了排序,快速确定凸包边界,极大地缩短了凸包的求取速度。
3.2 凸包求取
在求取平面散乱点集的凸包算法中,对于点集的无序性必须进行处理。很多算法没有对这些散乱点集进行预处理,从而导致算法复杂且易出错。通过对上述散乱点集进行预处理排序、删除多余顶点,得到一个有序多边形,下面就以图5(e)所示的多边形为例介绍凸包的求取。
(1)选取左下角的顶点为参考点。
(2)利用向量叉积的符号代表向量旋转方向这一特性,按照逆时针方向对得到的顶点按照极角大小进行排序。
(3)通过第二步的处理得到有序顶点序列,利用凸包连续的三个矢量顶点的凹凸性,当叉积S小于零时将顶点从栈中删除,当S大于零时将顶点压栈。
该凸包算法对极角进行排序时利用叉积符号代表旋转方向这一特性可以避免计算小数的误差。采用栈结构根据叉积进行凹凸性判断,这样依次删除所有凹点,最终保留下来的点为凸包子集。
4 算法分析与测试结果
4.1 效率分析
根据上述处理,可知凸包算法求取主要分为:
(1)散乱点集的预处理。通过寻找极值点删除一定不再凸包上的点,之后通过一边扫描排序法,再删除一些特殊的点同时实现剩余点集的有序性,最终对有序点集按照极角进行排序。
(2)凸包求取。利用凸包连续的三个矢量顶点的凹凸性,通过计算叉积来求取平面点集的凸包。
上述过程中对于点集的预处理,寻找极值点的时间复杂度是o(n),将点集划分为子集的时间复杂度是o(n)。由目前内部排序算法理论可知,对点集进行排序的算法最坏时间复杂度为o(nlogn)。对点集按照极角排序的时间复杂度是o(n)。由上述可知,文中提出的平面点集凸包求取算法的时间复杂度最坏是o(nlogn)。
4.2 测试结果
这里用产生随机数的方法生成散乱点集,并将传统算法与文中算法的运行速度进行多次比较,结果用C#编程获得,如图6所示。

图6 算法运行结果
程序中通过多次比较传统算法与文中算法的平均运行时间,其结果如表1所示。

表1 运行时间对比
5 结束语
基于海量数据的二维凸包快速生成算法通过对散乱点集分区、扫描等预处理,去除肯定不在凸包上的点集,避免了对不必要点集的处理,快速处理边界中的共线点集,缩小了问题规模。在生成边界的同时又对边界数据进行排序,使散乱的数据变得有序,极大提高了数据的处理能力以及凸包的生成速度。通过测试与对比,证明了基于海量数据的二维凸包快速生成算法在面对海量数据时,处理效果较好。因此该课题具有一定的理论研究意义和应用价值。
[1] Duncan J S,Ayache N.Medical image analysis:progress over decades and the challenges ahead[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2000,22(1):85-106.
[2] Day A M.Planar convex hull algorithms in theory and practice[J].Computer Graphics Forum,1998,7(3):177-193.
[3] 程三友,李英杰.一种新的最小凸包算法及其应用[J].地理与地理信息科学,2009,25(5):43-45.
[4] 吴雪刚.凸包算法和最近子空间分析及其在人脸识别中的应用[D].重庆:重庆大学,2014.
[5] 刘广忠,黄琳娜.平面散乱点集凸包的快速生成算法[J].工程图学学报,2008,29(4):111-114.
[6] 刘宏兵,邬长安,周文勇.基于二维凸包的TSP算法[J].计算机工程与设计,2009,30(8):1954-1956.
[7] Sklansky J.Measuring concavity on rectangular mosaic[J].IEEE Transactions on Computers,1972,C-21(12):1355-1364.
[8] 孔德慧,马春玲.一种平面点集凸包与三角网格综合生成的算法[J].计算机研究与发展,2000,37(7):891-896.
[9] 吴文周,李利番,王结臣.平面点集凸包Graham算法的改进[J].测绘科学,2010,35(6):123-125.
[10] 毛 鹏.快速凸包计算实现及其应用[D].西安:西安电子科技大学,2013.
[11] Chen C L.Computing the convex hull of a simple polygon[J].Pattern Recognition,1989,50(5):561-565.
[12] Preparata P F,Hong S J.Convex hulls of finite sets of points in two and three dimensions[J].Communications of the ACM,1977,20(2):87-93.
[13] 李军辉,李紫阳.GIS中散乱点集凸包的快速算法及编程[J].北京联合大学学报:自然科学版,2009,23(3):32-34.
[14] 金文华,何 涛,刘晓平,等.基于有序简单多边形的平面点集凸包快速求取算法[J].计算机学报,1998,21(6):533-539.
[15] 刘 波,万冉冉,阮 见,等.GIS中空间数据最小凸包串行算法的改进[J].测绘科学,2015,40(6):81-83.
Fast Algorithm for Generating Two-dimensional Convex Hull Based on Mass Data
MA Jun1,LIN Dong-jie1,LING Guang-ming2
(1.College of Computer and Information Engineering,Henan University,Kaifeng 475004,China; 2.School of Software,Henan University,Kaifeng 475004,China)
The convex hull algorithm is one of the fundamental problems in computer geometry and has been widely used in many fields.Traditional convex hull generation algorithm in dealing with large amounts of data shows high time complexity relatively and the lower rate of convex hull generation,which has been unable to meet the needs of actual data.In order to solve this problem,a fast convex hull algorithm of massive data in the face is proposed.Through a series of pre-processing operations of determining the scattered point set boundary and fast processing of boundary points concentrated in collinear points by partition and over scan sort of scattered point set,the algorithm quickly rules out the points inside the convex hull and reduces the size of the problem,to avoid the processing of assemblies that are not in the convex hull of point scanning,significantly shortening the calculating time of the convex hull,which can ensure the rapid generation of minimum convex hull.The algorithm is extremely simple,with low time complexity,achievingo(nlogn)theoretically.Itisconducivetoimprovethespeedofconvexhull.Comparedwiththetraditionalalgorithm,theexperimentalresultsshowthattheproposedalgorithmiseffectiveandhasgoodapplicationprospects.
convex hull;mass;planar point set;pretreatment;sort;fast
2016-04-13
2016-08-10
时间:2017-01-10
国家自然科学基金资助项目(61202098)
马 骏(1964-),男,教授,硕士,研究方向为空间信息处理、分布式并行计算及网络应用;蔺东杰(1990-),男,硕士,通讯作者,研究方向为空间信息处理、分布式并行计算及网络应用。
http://www.cnki.net/kcms/detail/61.1450.TP.20170110.1028.068.html
TP
A
1673-629X(2017)02-0042-04
10.3969/j.issn.1673-629X.2017.02.010
