斜辊钢管矫直过程的数值模拟与接触状态分析

王式研++马立东+++陈敏

摘 要：对某厂六斜辊（2-2-2）矫直过程进行显式动力学有限元分析，模拟各矫直辊快开压下过程及稳定矫直过程，仿真获得矫直力与现场压力传感器测试值基本一致。通过有限元后处理结果中矫直力随时间的历史变化曲线，分析了矫直过程中压弯力、压扁力的作用情况以及各接触对的接触特性变化。各单辊矫直力在矫直辊快开压下并接触钢管时最大，稳定矫直后趋于平稳，中间对辊接触相对比较均匀，边辊的接触区域集中在矫直辊的端部。

关键词：钢管；斜辊；矫直；数值模拟；接触

1 概述

随着机械工业的发展以及对输油管线铺设效率提高的迫切需要，对钢管成品的直线度及圆度精度要求越来越高。钢管矫直的直线度决定于反弯曲率与接触曲线，而圆度精度决定于压扁量。对于矫直机设备而言，直线度决定于反弯量和矫直辊的倾斜角，圆度决定于对辊辊缝。前苏联的马斯吉列逊[1]和国内的崔甫[2]对钢管矫直过程进行了系统的研究，对国内钢管矫直机设备及工艺的研究提供了基础。李强[3]采用在矫直辊轴承座上贴应变片的方式进行了斜辊钢管矫直机矫直力的测试分析。朱美珍[4]以弹塑性理论为基础，建立了压扁力的计算体系。于风琴[5]采用相对更准确的受力模型计算各矫直辊的受力情况，综合分析弯曲力与压扁力对总矫直力的作用，但其只在中间抱辊施加了压扁力。而在钢管实际矫直过程中，矫直辊的受力情况及其复杂，而且在实际矫直过程中，为了实现碾压弯曲矫直钢管端部作用，首尾对辊也要施加一定的压扁力。文章以某现场的实际工况为基础，建立有限元模型，分析矫直过程中矫直力的变化以及矫直辊接触情况。

2 有限元模型建立

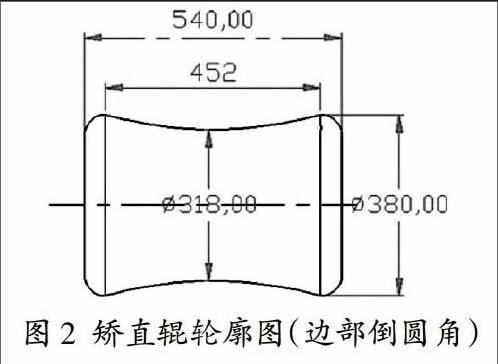
现场使用矫直机为国外引进当前国际先进的矫直机，具备完善的自动控制系统，能够实现矫直辊位置和角度的自动设定，同时，在三个上辊装配连接位置配备压力传感器，能够动态获得矫直过程中的矫直力。该矫直机矫直钢管外径尺寸范围60.3mm～244.5mm，壁厚范围3.5mm～30mm，最大允许矫直力100吨，矫后直线度精度能够达到管体1mm/1500mm，管端（1400mm范围）达到1mm/1000mm；首尾矫直辊辊距1800mm，辊腰直径318mm，辊形长度452mm。

矫直钢管为L80-1油套管，外径73mm，壁厚5.51mm，到达矫直机的温度为500℃。经过现场观测来料情况，来料钢管均相对比较直，肉眼观测无明显弯曲。

控制模型中输入参数为来料参数，分别为管徑73mm，壁厚5.5mm，屈服强度400Mpa；输出参数为三个上辊角度、三个下辊角度、三对辊辊缝值与中间下辊反弯量；设定参数为实际矫直过程中使用的三个上辊角度、三个下辊角度、三对辊辊缝值与中间下辊反弯量（弯曲形式为上弯式，中间下辊上抬），但是由于矫直辊的磨损，实际的辊缝值与设定值已经有非常大的差距，而现场矫直辊与钢管的接触状态良好，且能够矫直，因此模拟中选择了按照模型计算参数进行建模。穿管速度40m/min，矫直速度50m/min。

2.1 几何模型的建立

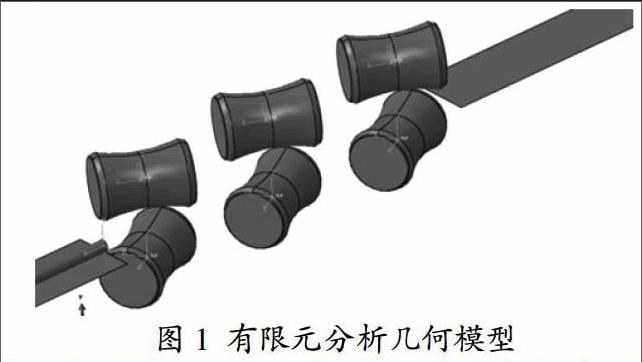
图1所示为建立的几何模型，涉及到的零件有矫直辊、钢管、辊道，其中为简化计算，辊道采用光滑无摩擦的平板代替。具体几何参数如表1所示。

矫直辊的辊形如图2所示将该辊形与现场矫直机矫直辊的样板辊形比较，两条曲线一致。

将钢管、矫直辊、平板按照现场尺寸进行装配，得到图1所示几何模型。

2.2 材料模型

矫直过程中辊系变形极小，故将辊系考虑为刚体，仅考虑钢管的变形，500℃时其可近似为理想弹塑性材料，相关物性参数参考现场经验，取弹性模量175Gpa，泊松比0.3，屈服强度400Mpa，500℃条件下，材料可近似看作理想弹塑性材料。

2.3 边界条件处理

整个计算过程完全参考现场实际矫直过程，初始状态各矫直辊沿自己的轴线空转，保证沿轧制方向分速度为50m/min，只有旋转自由度，其他方向固定，钢管给定初始速度场，穿管速度40m/min，两侧平板固定。当钢管经过第一对矫直辊时，入口上辊压下，经过第二对矫直辊时，中间上辊压下，经过最后一对矫直辊时，出口上辊压下，整个过程分为8个分析步，分别为初始步、开始穿管步、入口上辊压下步，穿管步，中间上辊压下步，穿管步，出口上辊压下步，连续矫直步。设置钢管与各矫直辊的接触为面面接触，径向有限滑动摩擦，摩擦系数0.2，法向硬接触；设置钢管与两侧平板为径向无摩擦接触，法向硬接触；总计8个接触对。

2.4 单元划分

钢管单元选择一阶显式六面体缩减积分单元C3D8R。划分钢管单元时保证钢管壁厚方向至少有4层单元以减小沙漏效应。

2.5 求解过程

为提高计算效率，计算过程中采用了半自动的质量放大办法，将时间增量步小于1E-6的值均放大到1E-6以上。

3 结果比较

3.1 矫直力结果比较

对现场矫直某根φ73钢管的控制模型上的视频录像进行分析，图3所示为视频上记录下来的三个上辊矫直力（t）随时间变化情况（现场上辊安装有压力传感器，钢管长度12m），图4为有限元计算过程各辊矫直力（N）变化曲线（其中下面3条对应上辊矫直力，钢管长度6m），从图中可以看到，曲线趋势相同，考虑有限元计算中的波动噪音，最大值偏差在15%以内，平均值偏差在20%以内。从结果来看，有限元计算模型相对准确。

3.2 直线度比较

根据现场实际检测，矫后的钢管均能满足1mm/1500mm的直线度要求。

为得到有限元分析后处理中具体的钢管直线度数据，采用的办法是分别在钢管最上边缘取一系列不间断节点，建立其坐标曲线1，然后取曲线1上的头尾节点，建立坐标直线2，将两条数据点相减可得到该边缘上任意节点的坐标差值。如图5所示是X方向钢管边缘的直线度数据。可以发现，在管体全长（6m）范围的最大挠度为0.25mm，远远低于1mm/1500mm。

图6所示为Y方向钢管边缘的直线度数据，管体全长部分（6m）最大挠度为0.16mm，且弯曲度变化较大的位置在钢管头尾500mm范围，直线度精度比较高。可以表明该有限元模型相对比较准确。

4 结果分析

从图4可以分析得出，钢管在进入入口辊时，入口上下辊受力较小，当入口上辊快开压下后，入口对辊开始承受矫直力，此部分矫直力均为压扁力，而上辊承受的矫直力稍大于下辊，原因是未进入辊系的钢管部分与辊道接触，抵消了部分向上的力，并且管端快速与中间下辊接触，由于中间下辊的反弯作用，入口上辊增加了承受单侧弯曲的力；随后，中间上辊快开压下，此时中间对辊矫直力迅速增大，而当出口上辊快开压下后（3.3s时），中间下辊所承受的力有增大的过程，此时，在整个辊系当中形成一个弯曲单元，中间下辊既承受压扁力，又承受压弯力，而中间上辊只承受压扁力。随后出口对辊与钢管接触，而出口上辊的力大于出口下辊的力，原因与入口上辊一致。由此可知入口下辊、中间上辊、出口下辊只承受对应辊缝的压扁力，而入口上辊、中间下辊、出口上辊除承受压扁力外还要承受压弯力，且中间下辊的反弯力应与入口上辊和出口上辊所受弯曲力之和一致。

矯直辊的实际接触情况对于矫直力能有直接影响，接触区域越大，压扁力越大。图7为稳定矫直时三个上辊的接触情况（左侧为入口辊），图8为稳定矫直时三个下辊的接触情况。从接触状态来看，中间上下辊均接触良好，入口上辊中间和偏右部分接触，入口下辊矫直辊左端接触，出口辊上辊全长接触良好，出口下辊右端接触更厉害，由此可以看出，形成弯曲单元后，矫直辊的接触状态比较复杂，但大的趋势是上辊边辊内侧接触多，而下辊边辊外侧接触多，而边辊接触区域的变化随着压扁量大小变化（模拟中出口压扁量大于入口压扁量）。

5 结束语

利用数值分析方法能够真实的模拟钢管斜辊矫直过程，矫直力与现场实测矫直力一致，钢管直线度满足要求，符合实际生产情况。计算结果表明中间下辊、入口和出口上辊承受压扁力和弯曲力，而中间上辊、入口下辊和出口下辊只承受压扁力。而压扁力的大小与接触区域相关，实际的接触区域比较复杂，中间对辊接触相对均匀，边辊接触出现端部集中现象。

参考文献

[1]马斯吉列逊，等.管材矫直机[M].西安重型机械研究所译.北京：机械工业出版社，1979.

[2]崔甫.矫直原理与矫直机械[M].第二版.北京：冶金工业出版社，2002.

[3]王秀军，李强，贾志刚.斜辊钢管矫直机矫直力计算分析[J].焊管，2002，27（2）：26-28.

[4]朱美珍，王春香，刘玉瑛.对向六斜辊管材矫直机压扁力研究[J].包头钢铁学院学报，1997，16（1）：36-41.

[5]于凤琴.钢管矫直机力能参数研究[J].试验与研究，2008，37（5）： 26-29.