基于格子Boltzmann理论的弱胶结裂隙岩体水沙两相流特性

浦 海，倪宏阳，肖 成

(1.中国矿业大学 深部岩土力学与地下工程国家重点实验室，江苏 徐州 221116；2.中国矿业大学 力学与建筑工程学院，江苏 徐州 221116)

基于格子Boltzmann理论的弱胶结裂隙岩体水沙两相流特性

浦 海1,2，倪宏阳2，肖 成2

(1.中国矿业大学 深部岩土力学与地下工程国家重点实验室，江苏 徐州 221116；2.中国矿业大学 力学与建筑工程学院，江苏 徐州 221116)

通过格子Boltzmann方法对裂隙岩体水沙两相流动规律进行理论分析，建立裂隙岩体水沙两相流动的格子Boltzmann模型，推导了水沙两相的基本守恒方程并建立了水沙两相流动系统的控制方程，基于浸入边界法，利用欧拉点和拉格朗日点处理水沙两相界面。通过数值模拟裂隙溃沙情况，分析了沙粒进入裂隙前后的流动形态，研究了颗粒粒径和裂隙宽度对溃沙速度的影响。借助单裂隙下的研究结果，建立上覆厚松散沙层矿井开采模型，分析裂隙发育下突水溃沙情况，发现在初始阶段，沙粒的溃入会堵塞裂隙，抑制裂隙的发育；随着水压的持续施加，大量水沙混合物开始涌入裂隙，岩体孔隙压力增大，导致裂隙迅速发育扩展，甚至会造成顶板垮落，加剧突水溃沙灾害。

格子Boltzmann理论；弱胶结裂隙岩体；水沙两相流；突水溃沙；保水采煤

我国西部矿区生态环境脆弱，浅埋煤层开采极易受到突水溃沙威胁，韩树青[1]、范立民[2]等最早进行突水溃沙灾害形成机理的研究，随后，范立民等探讨了矿井溃沙灾害形成的地质环境、防治思路及方法[3-4]，缪协兴[5-6]、范立民等[7-8]提出了规避突水溃沙灾害发生、保护地下水资源的“保水采煤”思路，王双明等[9]划分了保水开采地质条件分区，范立民等[10]对西部生态脆弱矿区矿井突水溃沙危险性进行了分区。

近年来，关于突水溃沙的研究在不断深入。梁燕等[11]对第三系弱胶结砂岩底板的突水突沙现象进行了模拟，并给出了机理分析；汤爱平等[12]通过对某矿井弱胶结粉沙突水涌沙机理的研究，给出了粉沙压力、水力坡度、溃沙量及突水量与时间的关系；张敏江等[13]发现第三系弱胶结砂岩突水涌沙的阶段性的特点以及粉砂岩易发生突水涌沙现象；Hu等[14]研究了西部风积沙区高强度开采下的变形特征；Pang等[15]基于三轴渗流试验提出了煤层顶板突水的力学模型；隋旺华等[16]借助室内试验发现含水层内孔隙水压力的变化可以作为近松散含水层开采时溃沙灾害预警的前兆信息；隋旺华等[17]通过试验研究了松散层突水溃砂与水力坡度及裂缝宽度的关系，指出初始水头和突水裂缝展开程度是影响突水溃砂的关键因素；杨伟峰[18]通过试验研究了水沙运移过程中孔隙水压力变化规律；许延春[19]研究了上覆含黏砂土的流动性，发现含黏砂土的渗漏自愈性，指出砂土是否稳定的关键因素是漏斗出口直径。

由于地下采掘工程的隐蔽性，学者多是借助室内模拟试验研究突水溃沙机理，但是试验研究很难去模拟突水溃沙发生过程中岩石裂隙的发育，限制了现阶段的研究。目前并不能对灾害类型和规模进行准确定量预测，也不能提供快速有效的治理措施，突水溃沙灾害发生机理和防治措施的研究亦尚不到位。为此，本文借助格子Boltzmann方法针对性的研究在单裂隙及裂隙发育过程中的水沙运移规律，其成果将为西部高强度下的煤炭安全开采及环境保护提供一定的理论和技术依据。

1 基于格子Boltzmann方法的裂隙岩体水沙两相作用分析

1.1 格子Boltzmann方法的水沙两相流守恒方程

任何物体的运动都遵循基本力学定律，在微观运动中，每个粒子都做无规则的热运动，研究单个微观粒子的运动并无太大意义，因此，可通过研究大量分子的运动，之后进行统计平均，从而求解出宏观物体的物理参数。另外，通过统计分子在某一状态的概率，而不是去研究单个分子的运动状态。基于这一思想产生了Boltzmann方程，运用统计力学观点研究微观粒子在不同状态下分布的变化，其分布函数f满足Boltzmann方程[20]，即

式中，Ω(f)为碰撞积分或碰撞项;r为空间位置矢量;ξ为分子速度矢量；a为分子所受到的加速度矢量。

1954年，Bhatnagar,Gross和Krook[21]提出用线性算子来代替Boltzmann方程中的积分项，即认为碰撞的效应是改变其密度分布函数f使其趋于平衡态分布feq，令

式中，τ0为松弛时间。

宏观运动是大量微观粒子运动的集合，少数微观粒子的运动并不会决定宏观运动，由此可将Boltzmann方程在速度上进行离散，从而在时间和空间上离散。离散后含有外力项的格子Boltzmann方程为

fα(r+eαδt,t+δt)-fα(r,t)=

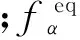
基于连续介质理论的水沙两相流动问题，每一相均需满足质量守恒方程、动量守恒方程及能量守恒方程等基本方程。对于质量m和动量mξ这些碰撞不变量，其输运方程为

以φ=m代入式(1)得质量守恒方程，即流体力学中的连续方程

式中，ρf为流体密度;vf为流体的宏观速度矢量。

同理，以φ=mξ代入式(2)，得流体力学中的动量方程为

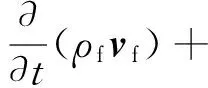
式中，σ为应力张量。

从式(3)和式(4)可知，流体力学中的质量守恒方程和动量守恒方程都可由LBM推出。因此，通过格子Boltzmann方法来研究流场分布在理论上是完全可行的。

1.2 裂隙岩体水沙两相流的格子Boltzmann模型

1.2.1 流动控制方程

本节建立裂隙岩体水沙两相作用力学模型，为后文研究水沙两相在裂隙岩体中的流动提供理论基础。其中，忽略水的可压缩性，用格子Boltzmann方程作为流场的演化方程，对于二维两相流动问题，采用D2Q9基本模型[22]，如图1所示。

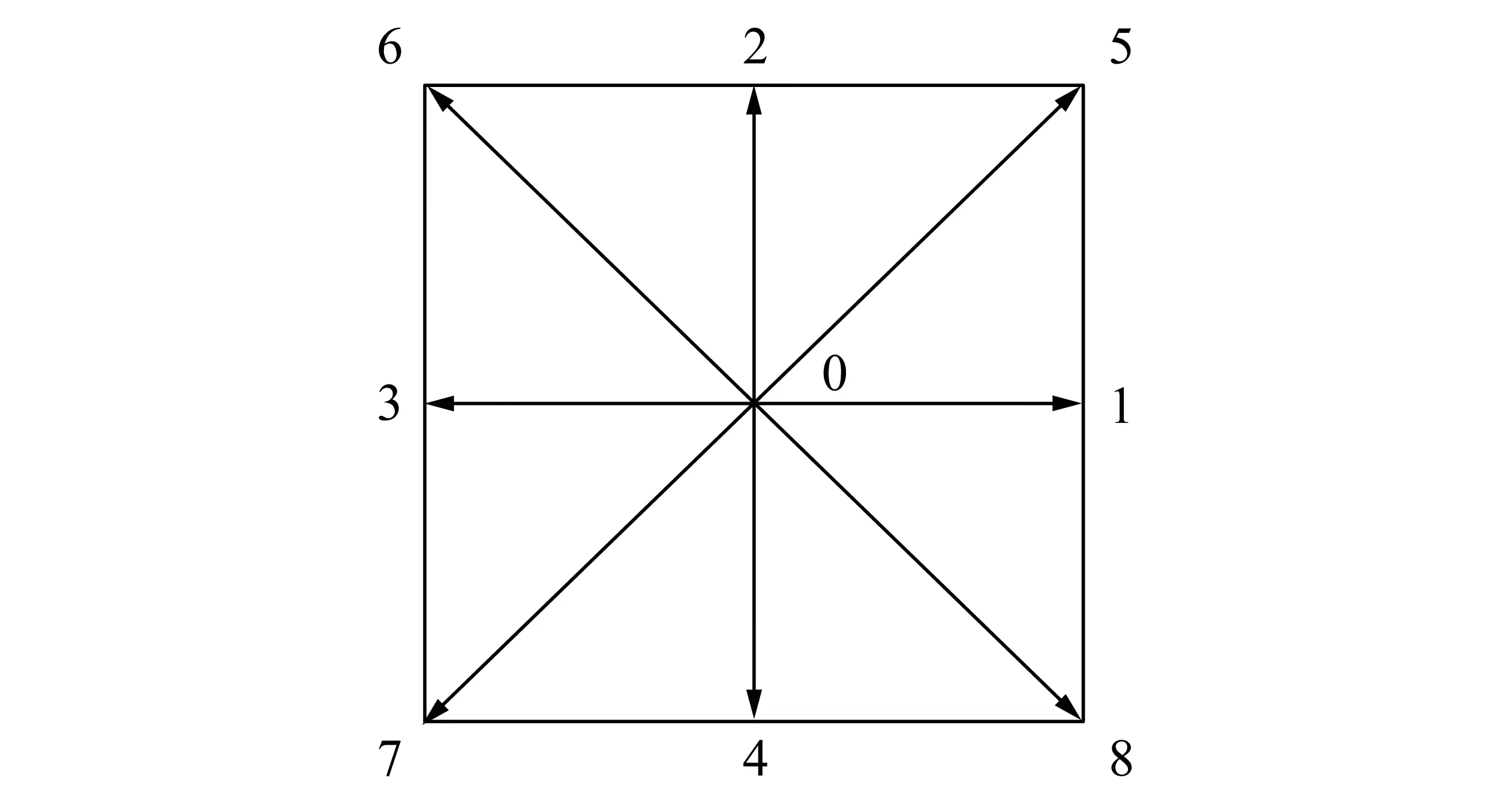
图1 D2Q9模型

D2Q9模型的9个离散速度取值见式(7)，设离散的流场区域方格边长为h。

式中，c为格子速度。

其平衡态分布函数为

其中，ωα为权系数。为恢复宏观方程，平衡态分布函数必须满足下列方程

将式(8)代入式(9),(10)并整理，可求得

则流体的宏观密度和宏观速度为

1.2.2 颗粒-流体两相边界处理

流场采用欧拉网格划分，每个方格节点定义一个流体的密度分布函数，颗粒在流体中运动时，两相边界的空间位置矢量随着颗粒的运动而变化，因此，用拉格朗日点划分两相边界[23]，如图2所示。

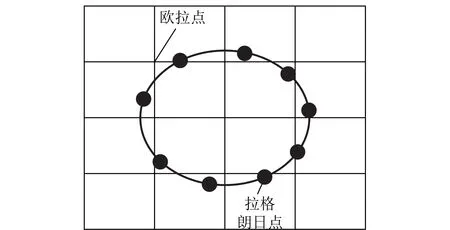
图2 浸入边界法示意

流体在拉格朗日点处密度分布的求解采用周围流体点数值外推，则拉格朗日点的密度分布函数为

其中，Xl(X,Y)为拉格朗日边界点坐标，此处用三阶多项式外推;imax和jmax为坐标水平方向和竖直方向的欧拉点数目，每个拉格朗日点取9个欧拉点进行计算取平均值，为表征两相边界对流场的影响，通过速度修正拉格朗日点处的密度分布函数，即

其中，β方向与α方向相反;UBC为朗格朗日节点的移动速度。流体和颗粒间动量守恒，力密度函数为

同理，流场受到颗粒的扰动，有

式中，Δsl为边界单元的弧长;u为节点移动速度;Dij控制颗粒对流体的作用只限于边界。

其中

因为加入了一个体力，因此，流体动量为

另外，颗粒对流体的反作用力存在两相边界，有

将固体颗粒边界受到的各个点的力合成，得颗粒质心受到的合力和合力矩为

2 单裂隙水沙运移数值分析

通过数值软件模拟沙粒在竖直裂隙中的流动形态，为使沙粒在进入裂隙前的流动形态能够更好的展现，将相同属性的沙粒分为6层，每层沙粒用不同颜色标出，颗粒参数取值见表1。

表1 模拟颗粒细观参数

Table 1 Simulated particle micro parameters

物理参数密度/(g·cm-3)粒径/mm杨氏模量/GPa泊松比摩擦角/(°)取值2.560.1～0.64.90.337模型参数法向刚度/GPa切向刚度/GPa摩擦因数阻尼系数孔隙率取值1.01.00.30.8930.35

沙层颗粒模型厚度90 mm，每层厚度15 mm，宽度240 mm，沿沙层宽度方向在各层中间每隔60 mm取一个颗粒，共3组18个颗粒，监测其运动轨迹。图3为各监测点位置以及编号。

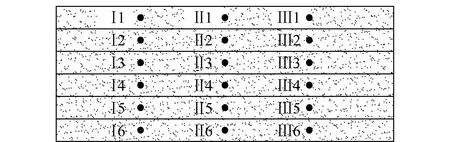
图3 监测点位置

根据表1中各参数建立数值模型观察颗粒的流动形态。在宽240 mm、高90 mm的墙体内部生成颗粒，颗粒在自重作用下达到稳定后，将其平均分为6层，删除上部墙体，裂隙采用墙体表示，在进行颗粒流动模拟时，通过在生成颗粒的矩形区域内设置不同水压模拟颗粒流动，数值模型如图4所示。

图4 沙粒流动数值模型

根据上述监测的3组18个点，得到沙粒流动形态如图5所示。

图5 沙粒流型

从流型中可以发现，稳定流动时，沙粒在进入裂隙前的流动形式为：

(1)在沙粒进入裂隙前，其流动形式为漏斗状流动。随着沙粒不断通过裂隙流出，上覆沙层形成的漏斗形状变得越来越尖。流动形态在流速稳定时坡面均匀下降，达到失稳流动时坡面非均匀下降。

(2)四周沙粒从静止开始逐渐向裂隙口运动，在进入裂隙前，基本呈现水平移动，越接近裂隙口，沙粒竖直方向速度越大，当进入裂隙后，其竖直方向的速度已经达到几乎与水平速度相等，因此，可从从中看到，沙粒在刚进入裂隙口时，其速度基本与水平方向呈45°角。

(3)沙粒在进入裂隙后，运动轨迹为“S”形，颗粒在进入裂隙后具有一个较小的水平速度，颗粒受到水的动力粘度以及裂隙壁的碰撞，水平速度分量逐渐减小直至为0。

监测沙粒在入口处的速度，得出沙粒速度变化曲线如图6所示，可以看出，沙粒在裂隙流动过程大致可分为4部分，即，沙粒起动过程、稳定流动过程、不稳定流动过程及结束过程。

图6 速度随时间变化曲线

图7 漏斗开口半径随时间变化

从图5可以看到，颗粒稳定下落时裂隙上覆厚沙层下落区形成一个口径逐渐增大的漏斗。图7为上覆沙层下落漏斗开口半径随时间的变化，可知随着水沙混合物进入裂隙，上覆沙层漏斗开口半径逐渐增大，水沙混合物刚开始流动时，漏斗口半径增速较快，随着流动的稳定，漏斗口半径增速逐渐减小。在沙场无限大的流动过程中，漏斗口半径应无限增大，由于沙场墙体边界效应，半径增速减缓后趋于稳定。

为研究颗粒粒径和溃沙流动速度关系，保持裂隙宽度、水压大小及边界条件不变，分别设置颗粒粒径为0.1～0.2，0.2～0.3，0.3～0.4,0.4～0.5，0.5～0.6以及0.6～0.7 mm，得到不同颗粒粒径的流动速度曲线如图8所示。前5个粒径对应的流速为0.65,0.93,1.47,1.73,2.90 cm/s,可以看出，稳定流速伴随粒径的增大而增大，颗粒粒径对溃沙的启动时间有一定影响。

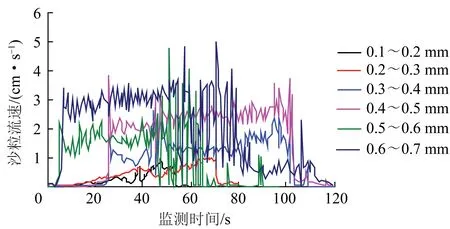
图8 不同粒径颗粒流速曲线

为研究裂隙宽度和流速的关系，保持颗粒粒径不变，监测裂隙宽度5,6,7,8,9,10 mm的流速曲线(图9),其对应的速度为2.31，2.83，3.21，3.32，3.31，3.52 m/s。可以看出，在稳定流速阶段，沙粒流动速度随着裂隙宽度增大而增大，且增长速度逐渐变小。考虑裂隙宽度和沙粒粒径的大小关系，当裂隙宽度增加到一定程度后，可以忽略其对沙粒速度的影响。

图9 不同裂隙宽度沙粒流速变化曲线

3 裂隙发育中水沙输运

浅埋煤层顶板在上覆厚沙土层作用下呈现整体下沉而不是离层运动，开挖后若岩层出现与沙层贯通的裂隙，水沙混合流入裂隙，水改变岩层含水性从而弱化岩层强度性能，沙粒促进裂隙发育，加剧突水溃沙灾害，甚至造成顶板垮落，给煤矿生产带来巨大的安全隐患。

借助单裂隙下的研究结果，可以进一步研究开挖后裂隙发育过程中的水沙输运。如图10所示，建立具有不同属性的岩层，岩层模型底部和左右两端均为固定边界，沙层颗粒接触借助线性接触模型，岩层则采用线性接触平行黏结模型，岩层上方生成沙粒且在自重作用下达到平衡，使用的参数见表2。

表2 弱胶结岩体细观参数

Table 2 Micro parameters of weakly cemented rock

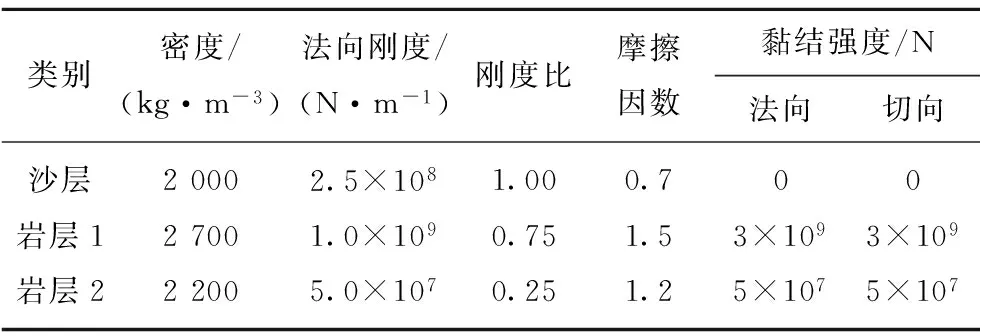
类别密度/(kg·m-3)法向刚度/(N·m-1)刚度比摩擦因数黏结强度/N法向切向沙层20002.5×1081.000.700岩层127001.0×1090.751.53×1093×109岩层222005.0×1070.251.25×1075×107

当地层开挖达到稳定后，从图11(a)中可以发现，开挖区上部出现少量裂隙，但此时只有少量沙粒进入裂隙，从图11(b)可以看出，并未影响地层的稳定性，此时，依旧处于安全阶段。

图10 模型上覆沙层示意

图11 开挖后裂隙分布与地层稳定对比

在施加5 MPa的水压之后，裂隙主要沿着竖直方向进一步发育，在开采层两侧产生大的贯通裂隙，这些裂隙成为水沙运移的主要通道，沙粒开始流入矿井。随着水沙涌入，在水力应力耦合作用下，顶板上少量横向裂隙进一步发育，顶板开始出现块状岩体脱落的现象(图(12))，直至最终两侧裂隙连通，顶板出现垮落现象，大量沙粒涌入矿井。

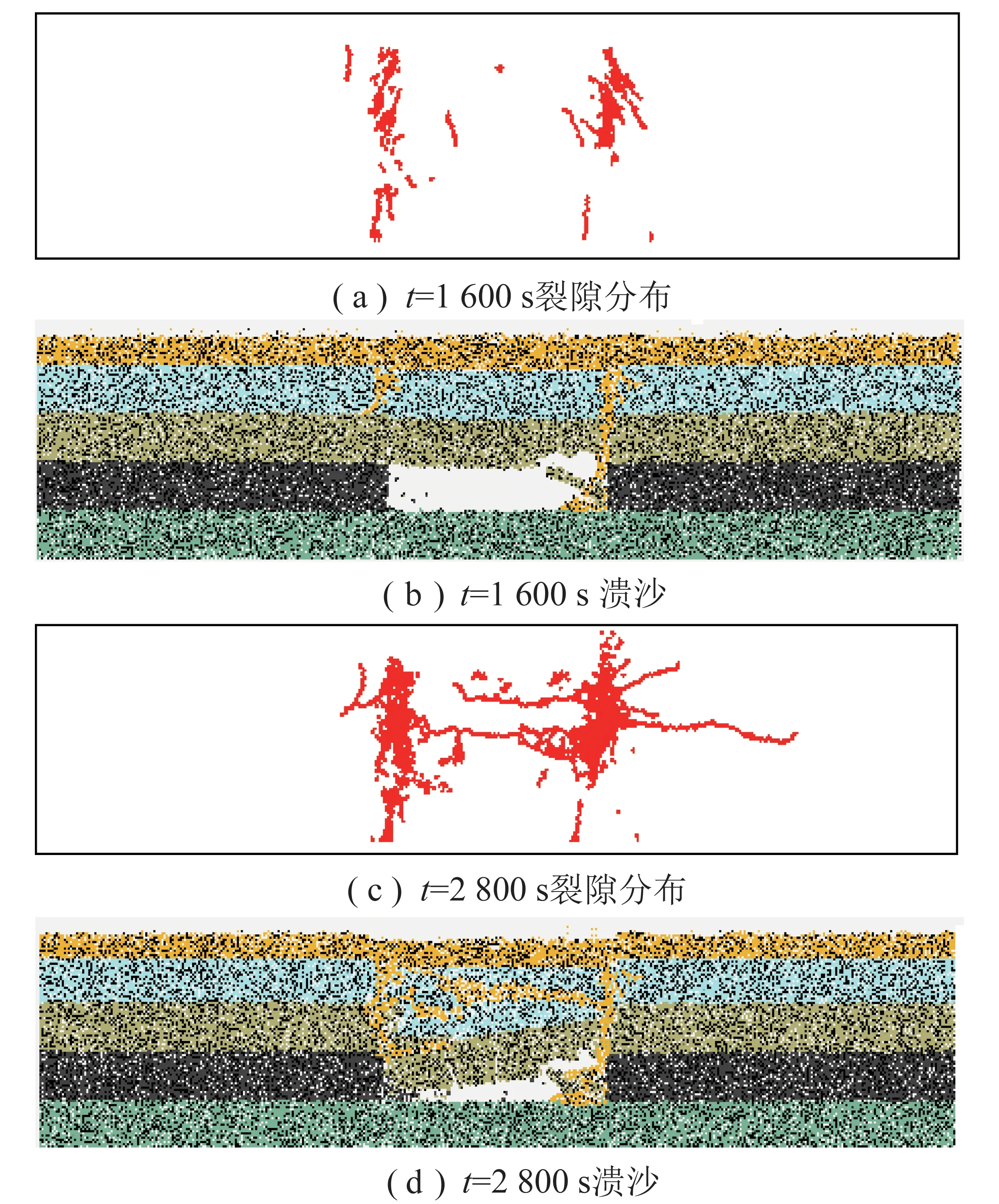
图12 不同时刻裂隙分布与溃沙对比

图13为裂纹随时间的发育情况，可以看出，裂纹数目并未一直增多，而是呈现阶梯形增长，说明在水沙流入裂纹后，水沙对裂纹生长具有一定的抑制，但随着随水沙的继续涌入，裂纹数目度过阶梯形平稳后又急速增加，此时，水沙填堵裂隙，使得孔隙内压力迅速增大，并在裂纹尖端产生应力集中现象。在岩层垮落前，裂纹数目一直处于阶梯形增长，如图12所示，t=2 000 s后，裂纹数目急剧增加，此时大块岩体垮落，微裂纹随着裂隙贯通迅速增多。

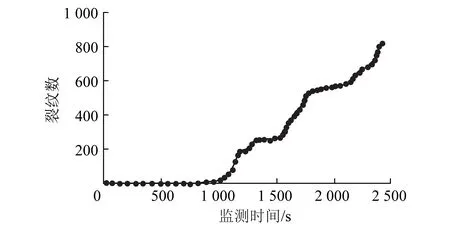
图13 裂纹数目随时间变化曲线

4 结 论

(1)推导了基于格子Boltzmann理论的流体力学的基本守恒方程。使格子Boltzmann方法、浸入边界法研究水沙两相相界面作用，通过欧拉网格点和拉格朗日点处理两相边界，得到两相界面处的流场分布函数，可以用于研究水沙两相流特性。

(2)沙粒在进入裂隙前呈现出漏斗状形态，且漏斗半径逐渐增大，但增大速率逐渐减小并最终趋于稳定；根据流动过程的速度曲线可以得出，沙粒的流动过程大致可以分为4个阶段，即，沙粒由静止开始运动的起动过程阶段、沙粒基本以稳定速度流动的稳定流动阶段、沙粒流动速度不稳定阶段以及沙粒流尽的结束过程；流速随着粒径的增大而增大，颗粒粒径对溃沙的启动时间有一定影响；流速随着裂隙宽度增大而增大，且增长速度逐渐变小，这是影响溃沙严重程度的关键因素。

(3)在裂隙发育未完全时，沙粒溃入在一定程度上能够抑制裂隙的发育，但随着水压的持续施加，大量沙粒开始涌入填堵裂隙，裂隙内的孔隙压力迅速增大，促使裂隙进一步发育，到达一定程度后，就会造成水沙突涌，沿着各新生的孔隙流入，进而加速裂隙发育过程，甚至造成煤层顶板的垮落，加剧突水溃沙灾害。

[1] 韩树青，范立民，杨保国.开发陕北侏罗纪煤田几个水文地质工程地质问题的分析[J].中国煤田地质，1992，4(1)：49-52. Han Shuqing,Fan Limin,Yang Baoguo.Some hydrogeological and engineering-geological problems concerning development of north Shaanxi Jurassic coalfield[J].Coal Geology of China,1992,4(1):49-52.

[2] 范立民.神木矿区的主要环境地质问题[J].水文地质工程地质，1992，19(6)：37-40. Fan Limin.Environmental geology in Shenmu mining area[J].Hydrogeology & Engineering Geology,1992,19(6):37-40.

[3] 范立民.神府矿区矿井溃沙灾害防治技术研究[J].中国地质灾害与防治学报，1996，7(4)：35-38. Fan Limin.Controlling technological study on suffosion hazard of coalshaft in Shenfu mining area[J].The Chinese Journal of Geological Hazard and Control,1996,7(4):35-38.

[4] Fan Limin.Study on geological disaster from water inrush and sandbursting in mine of shenfu mining distrct[A].Groundwater HazardControl and Coalbed Methane Development and Application Techniques—Proceedings of the International Mining Tech’96 Symposium.CCMRI[C].Xi’an,1996:154-161.

[5] 缪协兴，王安，孙亚军，等.干旱半干旱矿区水资源保护性采煤基础与应用研究[J].岩石力学与工程学报，2009，28(2)：217-227. Miao Xiexing,Wang An,Sun Yajun,et al.Research on basic theory of mining with water resources protection and its application to arid and semi-arid mining areas[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(2):217-227.

[6] 缪协兴，陈荣华，白海波.保水开采隔水关键层的基本概念及力学分析[J].煤炭学报，2007，32(6)：561-564. Miao Xiexing,Chen Ronghua,Bai Haibo.Fundamental concept sand mechanical analysis of water-resisting key strata in water-preserved mining[J].Journal of China Coal Society,2007,32(6):561-564.

[7] 范立民.论保水采煤问题[J].煤田地质与勘探，2005，33(5)：50-53. Fan Limin.Discussing on coal mining under water-containing condition[J].Coal Geology & Exploration,2005,33(5):50-53.

[8] 范立民，马雄德，冀瑞君.西部生态脆弱矿区保水采煤研究与实践进展[J].煤炭学报，2015，40(8)：1711-1717. Fan Limin,Ma Xiongde,Ji Ruijun.The progress of research and engineering practice of water-preserved coal mining in western eco-environment frangible area[J].Journal of China Coal Society,2015,40(8):1711-1717.

[9] 王双明，黄庆享，范立民，等.生态脆弱矿区含(隔)水层特征及保水开采分区研究[J].煤炭学报，2010，35(1)：7-14. Wang Shuangming,Huang Qingxiang,Fan Limin,et al.Study onoverburden aquclude and water protection mining regionazation in the ecological fragile mining area[J].Journal of China Coal Society,2010,35(1):7-14.

[10] 范立民，马雄德，蒋辉，等.西部生态脆弱矿区矿井突水溃沙危险性分区[J].煤炭学报，2016，41(3)：531-536. Fan Limin,Ma Xiongde,Jiang Hui,et al.Risk evaluation on water and sand inrush in ecologically fragile coal mine[J].Journal of China Coal Society,2016,41(3):531-536.

[11] 梁燕，谭周地，李广杰.弱胶结砂层突水、涌砂模拟试验研究[J].西安公路交通大学学报，1996，16(1)：19-22. Liang Yan，Tan Zhoudi，Li Guangjie.Simulation testresearch on water and soil outbursts of weak bindingsoil[J].Journal of Xi’an Highway University，1996，16(1)：19-22.

[12] 汤爱平，董莹，谭周地，等.振动作用下矿井突水涌砂机理的研究[J].地震工程与工程振动，1999，19(2)：132-135. Tang Aiping,Dong Ying,Tan Zhoudi,et al.Mechanism of sandy-silt seepage deformation in mineunder vibration[J].Earthquake Engineering and Engineering Vibration,1999,19(2):132-135.

[13] 张敏江，张丽萍，姜秀萍，等.弱胶结砂层突涌机理及预测研究[J].金属矿山，2002(10)：48-50. Zhang Minjiang,Zhang Liping,Jiang Xiuping,et al.Study on the inrushing mechanism of weak cemented quicksand layer and its forecasting[J].Metal Mine,2002(10):48-50.

[14] Hu Zhenqi,Chen Chao,Xiao Wu,et al.Surface movement and deformation characteristics due to highintensive coal mining in the windy and sandy region[J].International Journal of Coal Science & Technology,2016,3(3):339-348.

[15] Pang Yihui,Wang Guofa,Ding Ziwei.Mechanical model of water inrush from coal seam floor based on triaxial seepage experiments[J].International Journal of Coal Science & Technology,2014,1(4):428-433.

[16] 隋旺华，董青红.近松散层开采孔隙水压力变化及其对水砂突涌的前兆意义[J].岩石力学与工程学报，2008，27(9)：1908-1916. Sui Wanghua，Dong Qinghong.Variation of pore water pressure and its precursor significance for quicksand disasters due to mining near unconsolidated formations[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(9):1908-1916.

[17] 隋旺华，蔡光桃，董青红.近松散层采煤覆岩采动裂缝水砂突涌临界水力坡度试验[J].岩石力学与工程学报，2007，26(10)：2084-2091. Sui Wanghua,Cai Guangtao,Dong Qinghong.Experimental research on critical percolation gradient of quicksand across overburden fissures due to coal miningnear unconsolidated soil layers[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(10):2084-2091.

[18] 杨伟峰.薄基岩采动破断及其诱发水砂混合流运移特征[D].徐州：中国矿业大学，2009.

[19] 许延春.含黏砂土流动性试验[J].煤炭学报，2008，33(5)：496-499. Xu Yanchun.Fluidity test on sand blended with clay[J].Journal of China Coal Society,2008,33(5):496-499.

[20] Song Feifei,Wang Wei,Li J.A lattice Boltzmann method for particle-fluid two-phase flow[J].Chemical Engineering Science,2013,102:442-450.

[21] Mindlin R D,Deresiewicz H.Thickness-shear and flexural vibrations of a circular disk[J].Journal of Applied Physics,1954,25(10):1329-1332.

[22] 何雅玲，王勇，李庆.格子Boltzrrlann方法的理论及应用[M].北京：科学出版社，2009.

[23] Charles S Peskin.Flow patterns around heart valves:a numerical method[J].J.Comput.Phys.,1972,10(2):252-271.

Characteristics of water sediment two phase flows in weakly cemented fractured rock mass based on Lattice Boltzmann method

PU Hai1,2，NI Hong-yang2，XIAO Cheng2

(1.StateKeyLaboratoryforGeomechanics&DeepUndergroundEngineering,ChinaUniversityofMining&Technology,Xuzhou221116,China;2.SchoolofMechanicsandCivilEngineering,ChinaUniversityofMining&Technology,Xuzhou221116,China)

Theoretical analysis is taken on the water sediment two phase flows pattern of fractured rock based on lattice Boltzmann method and a model is built.Also,the basic conservation equations are derived and the control equations are established.The water and sand phase interface is analyzed by using the Euler point and Lagrange point based on the immersed boundary method.Numerical simulation is taken on sand inrush,and the flow patterns of sand moving in fracture is analyzed,the influence of particle size and fracture width on the velocity of sand inrush is studied.With the results in single fracture,a mechanical model of sand mining roof covered with thick loose is established to analyze water and sand inrush,the authors find that at the initial stage,the sand particles flowing in cracks can restrain its development,with the water pressure continually applied,a large number of water and sand mixture begin to flow in,which makes the pore pressure increase,causing the cracks rapidly develop,even causing the roof fall,aggravating the water and sand inrush.

Lattice Boltzmann Method (LBM);weakly consolidated fractured rock;water sediment two phase flows;water and sand inrush;water-preserved mining

10.13225/j.cnki.jccs.2016.5011

2016-10-02

2016-12-20责任编辑:张晓宁

国家重点基础研究发展计划(973)资助项目(2015CB251601，2013CB227900)；国家自然科学基金资助项目(51322401)

浦 海(1978—)，男，江苏盐城人，教授，博士生导师，博士。Tel:0516-83885205，E-mail:haipu@cumt.edu.cn

TD823

A

0253-9993(2017)01-0162-07

浦海，倪宏阳，肖成.基于格子Boltzmann理论的弱胶结裂隙岩体水沙两相流特性[J].煤炭学报,2017,42(1):162-168.

Pu Hai，Ni Hongyang，Xiao Cheng.Characteristics of water sediment two phase flows in weakly cemented fractured rock mass based on Lattice Boltzmann method[J].Journal of China Coal Society,2017,42(1):162-168.doi:10.13225/j.cnki.jccs.2016.5011