保水开采相似模拟高精度位移测量方法研究

张玉江，冯国瑞，戚庭野，康立勋，LUO Yi，章 敏，闫永敢

(1．太原理工大学 矿业工程学院，山西 太原 030024；2．山西省绿色矿山工程技术研究中心，山西 太原 030024；3．太原理工大学 采矿工艺研究所，山西 太原 030024；4．太原理工大学 建筑与土木工程学院，山西 太原 030024；5．Department of Mining Engineering，West Virginia University,Morgantown 26506,USA)

保水开采相似模拟高精度位移测量方法研究

张玉江1,2，冯国瑞1,2，戚庭野2,3，康立勋1,2，LUO Yi5，章 敏2,4，闫永敢1,2

(1．太原理工大学 矿业工程学院，山西 太原 030024；2．山西省绿色矿山工程技术研究中心，山西 太原 030024；3．太原理工大学 采矿工艺研究所，山西 太原 030024；4．太原理工大学 建筑与土木工程学院，山西 太原 030024；5．Department of Mining Engineering，West Virginia University,Morgantown 26506,USA)

针对保水开采相似模拟岩层大范围非线性位移特点和大量程高精度测量要求，提出了一种通过布设参考点提高位移测量精度的方法，并通过实验进行了分析验证。研究结果表明：测量精度随参考点个数及位移值的增加而提高；参考点个数增加可以减小系统误差，系统误差随着参考点个数的增加在一定范围内波动，测量值误差的正负决定波动趋势；当参考点个数大于15时，误差均值向有序过渡，大于25时，表现为有序状态；为保证测量精度，至少需要对25个参考点。本方法可为保水开采覆岩移动变形模拟观测提供借鉴。

相似模拟；覆岩移动；测量精度；系统误差；保水开采

保水开采是解决西部生态脆弱矿区浅埋煤层开采与生态平衡的重要方法[1-2]。保水开采通过各种技术措施控制覆岩(尤其是隔水关键层)的断裂与移动，实现对地表、地下水以及地表生态环境的保护[3]。虽然专家学者对隔水层及隔水关键层进行了理论研究[4]，但是更多的研究是通过相似模拟实验进行的[5-7]。为了更好的研究保水开采，开发了固流耦合相似模拟技术[8]，甚至专门研发了隔水层相似模拟材料[9]。然而西部生态脆弱矿区煤层开采具有浅埋、薄基岩、固流耦合特点，会造成覆岩大范围非线性移动[10-12]，对保水开采相似模拟位移测量的量程和精度提出了更高要求。但是，现有方法难以同时满足大量程和高精度要求[13]。全站仪测量法作为非接触测量方法，能很好地满足量程的要求，且仪器不受模型开挖扰动的影响应用广泛[14-15]。但是受环境及人为操作等因素的影响，其测量存在一定的误差，又因为实验受时间限制，多次测量求平均值存在一定困难。因此，亟需减小全站仪在相似模拟近距离位移观测中的误差，提高其精度。

目前，类似提高精度的方法为消除系统误差。德国联邦技术研究所[16]和日本计量院[17]将闭环测量技术应用于齿距偏差的纠正，娄志峰[18]将繁琐的闭环测量技术简化为2步分离出系统误差仍具有较高的精度。而测绘学中的测量平差理论是针对不动点，在各控制点分别测量且需要多余的观测值。文献[19]建立了三维扫描仪的系统误差模型，并利用空间坐标转换解算以减小系统误差。现有消除系统误差的方法难以适相似模拟覆岩移动大范围非线性的特点和大量程高精度测量要求。因此，本文提出了一种通过设立多个相对全站仪后视点不动的参考点方法，以减小测量时所产生的系统误差，达到提高测量精度的目的，可为提高保水开采相似模拟的可靠性提供借鉴。

1 研究方法

1.1 方法的提出

如图1所示，X为横坐标，表示水平方向，Y为纵坐标，表示竖直方向。A1，A2，A3，…，Ak，…，Am为参考点，B1，B2，B3，…，Bj，…，Bn为观测点，位于矩形观测区内。本文提出方法包括以下几个步骤：(1)在观测点的周围设置一系列相对于后视点O不动的参考点Ak，并与观测点一起进行测量；(2)对所有参考点进行误差分析，判断测量结果是否可用；(3)以参考点Ak为坐标原点进行坐标转换，得到单次观测的平均偏差，作为纠正值；(4)用纠正值纠正该次测量中观测点的位移值，得到纠正后的位移值。

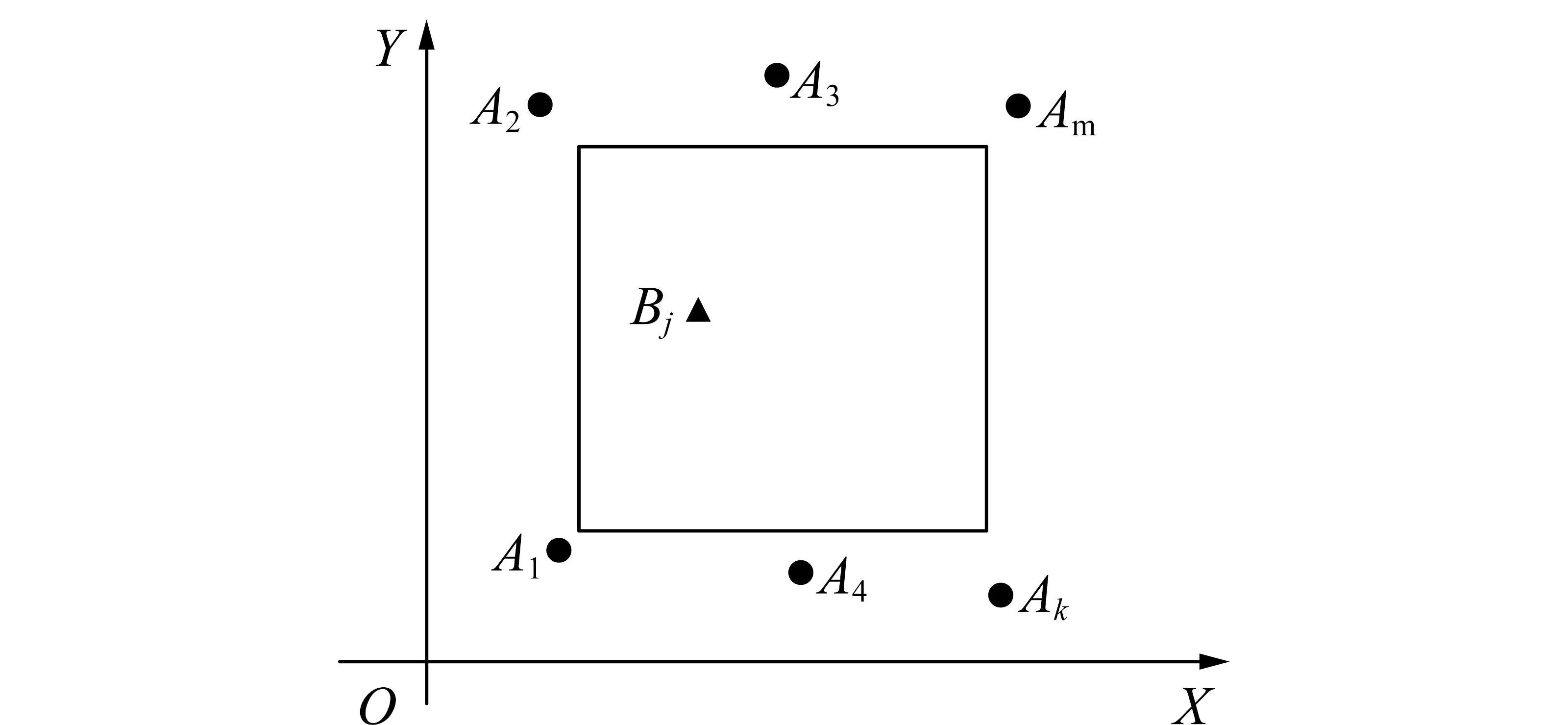
图1 参考点布置示意

1.2 带纠正值的位移值的理论分析

二维相似模拟位移观测仅涉及水平坐标X和竖直坐标Y。定义第i次测量的第k个参考点Aik的坐标是(xik，yik)，第j个观测点Bij的坐标为(uij，vij)，其中i表示为第i次观测。某观测点第i次观测的累计位移量分别由第i次测量的坐标减去第1次测量的坐标获得。

以后视点O为坐标原点时，第1次测量的参考点A1k的坐标为(x1k，y1k)，观测点B1i的坐标为(u1i，v1i)，第i次测量时，Aik的坐标为(xik，yik)，Bij的坐标为(uij，vij)。则第i次测量第j个观测点和第k个参考点的位移量D(Bij),D(Aik)分别为

D(Bij)=(uij-u1j+Δuij-Δu1j,vij-v1j+

Δvij-Δv1j)

D(Aik)=(xik-x1k+Δxik-Δu1k,yik-y1k+

Δyik-Δy1k)

式中，uij,vij分别为第i次测量第j个观测点的真值；Δuij和Δvij分别为第i次测量第j个观测点的水平及竖直误差；xik,yik分别为第i次测量第k个参考点的真值；Δxik和Δyik分别为第i次测量第k个参考点的水平及竖直误差。

为得到纠正值，分别以参考点A1，A2，A3，…，Ak，…，Am为坐标原点对坐标系XOY进行坐标系变换，分别得到不同坐标系下观测点的坐标。

式中，i=2,3,4，……；j=1,2,3，…，n；k=1,2,3，…，m。

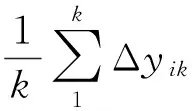
根据误差理论，可以将误差分为偶然误差和系统误差。以下分别为测量点和参考点在竖直方向的误差表达式：

式中，Δvij为第i次测量Bj点在竖直方向的误差，ΔAvij和ΔSvij分别为其偶然误差和系统误差；Δyik为第i次测量参考点Ak在竖直方向的误差，ΔAyik和ΔSyik分别为其偶然误差和系统误差。

将式(4)，(5)代入式(3)可得Y方向的累计位移均值为

将参考点在数值方向的误差均值作为纠正值即可以减小误差，提高测量精度。由式(5)可得纠正值为

由式(7)可知，当参考点个数k达到一定程度时，偶然误差的均值趋近于0[20]，则有

因观测过程中测量环境、仪器和观测人员一致，所以可认为单次观测的系统误差相同，即

根据式(6)，(8)和(9)可知，采用Cik作为纠正值，纠正同批次的测量值，可以达到降低系统误差，提高观测精度的目的，而剩余的测量数据中的偶然误差需多次观测即可减小。

1.3 实验方法

本次实验利用全站仪观测相似模拟实验中的岩层移动，以研究上述方法对其测量精度的影响。实验所用设备包括：NTS-330全站仪；GY500W工业相机；二维相似模拟支架，规格为长×宽×厚=3 m×2.4 m×0.2 m，其中相似材料铺设高度为2.1 m，上部为可以施加补偿载荷的气囊。

实验按照如下流程进行。如图1所示，在相似模拟观测面设置后视点、观测点和参考点，其中横坐标表示水平方向，纵坐标为竖直方向，矩形区域为观测点Bj所处区域，后视点为O，参考点共16个，分别布置在观测区域的上下两侧，依次为A1，A2，A3，…，A16。在观测侧合适位置分别设置控制点，架设全站仪和工业相机并进行校正、设置。准备完毕后，首先对各个观测点和参考点进行观测，然后进行开挖，开挖完毕后再对观测点和参考点进行观测，之后按照时间间隔依次进行开挖、测量。观测时间间隔为开挖时间间隔的2倍，96 min，共计观测6次。

2 结果及分析

2.1 精度分析

对16个参考点的竖直方向位移(下沉量)进行误差分析，分别得出控制点1和控制点2所得测量数据的误差，其下沉量的算术平均偏差和标准差见表1。

对参考点的多次测量发现，1,2号控制点测量数据的算术平均偏差的均值分别为0.34 mm和0.33 mm，其算术平均偏差的范围都为0～0.56 mm，而控制点2的相对误差均值和最大值均大于控制点1，均值分别为0.021%和0.075%，最大值分别为0.041%和0.210%。很小的算术平均偏差和相对误差都说明测量具有较高的精确度。

对参考点的多次测量发现，1,2号控制点测量数据的标准差均值分别为0.45和0.49 mm，标准差的范围都为0～0.75 mm。结合仪器精度，可以看出，测量具有较高的精密度。

2.2 误差的放大

虽然测量结果分析显示实验中测量有较高的准确度，但是，在相似模拟实验中，岩层下沉量是2次测量值的差值。实验中岩层的下沉量最大为5.0 cm(同类实验最大值均不超过十多厘米)，所以在计算岩层下沉量的过程中，误差会被放大。

表1 下沉量的误差

Table 1 Errors of subsidence value

按照测量数据的算术平均偏差的均值0.34 mm计算岩层下沉量增大过程中的相对误差，可以发现相对误差与岩层下沉量之间存在如图2所示的关系。

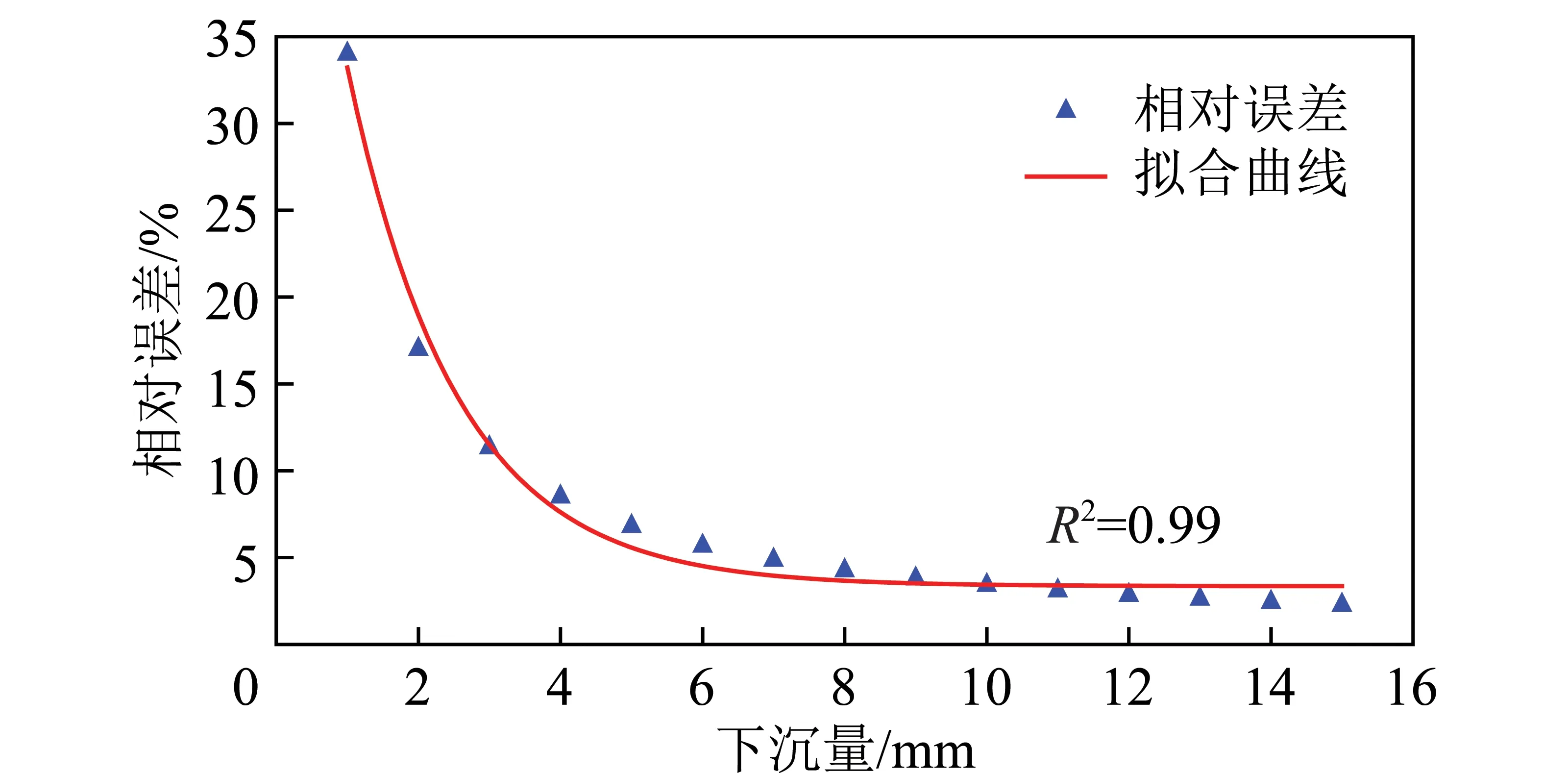
图2 相对误差和下沉量的关系

由图2可以发现，虽然算术平均偏差和相对误差相对测量值很小，但是相对于毫米级的下沉量来说，仍然可能超过允许误差。如图2所示，如要满足误差不超过5%的要求，则最小测量值为6.8 mm。这表明，对于控制点1来说，下沉量小于6.8 mm的观测点所得结果的误差都大于5%。

2.3 纠正值分析

为找出参考点个数与纠正值之间的关系，求出多次测量各个参考点的纠正值，得到它随参考点个数增加的变化趋势，如图3所示。

图3 纠正值随参考点个数的关系

如图3所示，纠正值随着参考点个数的增加，呈现由散乱向有序的发展过程，并且波动的振幅在减小。在参考点个数小于15时，参考点纠正值散落范围比较大，且散乱。当参考点个数增加到15～25时，振幅收窄，散乱程度明显改善，由散乱向有序过渡。当参考点个数大于25时，振幅进一步收窄，纠正值随参考点个数增加有序变化。有序后，控制点1和2的累计纠正值在-0.1～+0.1 mm和-0.05～+0.15 mm波动，即为多次测量误差的上下限。有序后，如果偏差的均值为正，则波动趋势向上，否则波动趋势向下。

理论上，随着参考点的增加或者观测次数的增加可以消除偶然误差，但是由于系统误差的存在，在实际测量中，纠正值沿某个值振动并趋近于该值。这个趋近值就是偶然误差之外的所有因素造成的误差。对于单次测量来说，这个趋近值就是该次测量中参考点的平均偏差，即纠正值。

2.4 纠正值确定及下沉量计算

分别计算6次测量中参考点下沉量的绝对误差和标准差，求平均得到该次测量的平均偏差和标准差，见表2。

表2 单次测量下沉量的平均偏差和标准差

Table 2 Mean variation and standard deviation in every single measure

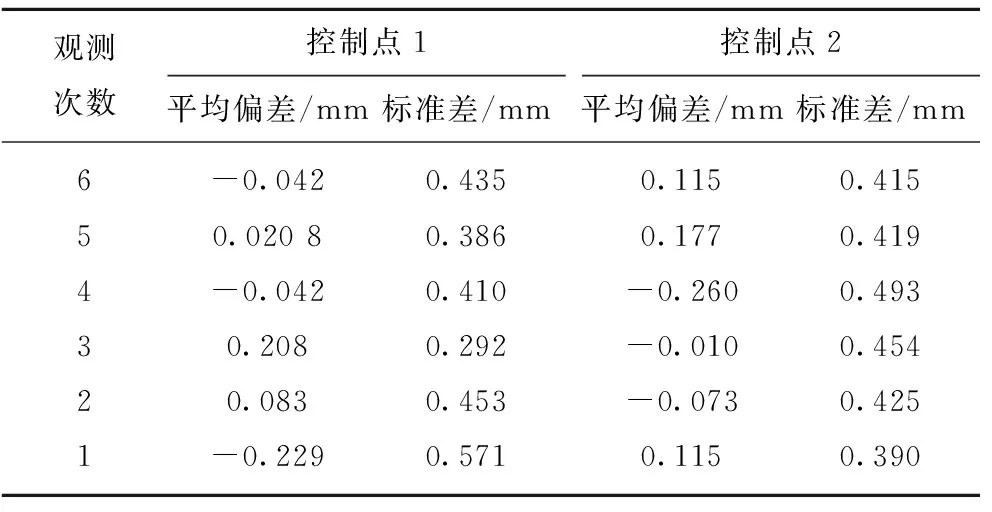
观测次数控制点1平均偏差/mm标准差/mm控制点2平均偏差/mm标准差/mm6-0.0420.4350.1150.41550.02080.3860.1770.4194-0.0420.410-0.2600.49330.2080.292-0.0100.45420.0830.453-0.0730.4251-0.2290.5710.1150.390

表2中，平均偏差为负，说明该次测量值偏小，平均偏差为正，说明该测量值偏大。在求解观测点的下沉量时，需要利用测量值减去本次测量的平均偏差。如对控制点1来说，第6次、第1次测量的平均偏差分别为-0.042 mm和-0.229 mm，说明两侧测量值均偏小，在根据测量值计算下沉量之后还需要加上第6次测量的平均偏差与第1次测量的平均偏差差值，即0.208 mm。同样可以得到控制点2，第6次测量所得下沉量的纠正值为0。如图4所示，将纠正后的下沉量制成下沉曲线，图中横坐标为距模型边界的距离，纵坐标为下沉量。测线1～6分别位于8号煤层之上，采高倍数k依次为12.0,9.1,6.6,5.1,3.1和1.5。

图4 纠正后的各测线下沉量

3 结 论

(1)参考点的设置可以提高观测精度，且测量精度随参考点个数的增加而提高，准确度随位移值增大而提高。全站仪具有较高测量精度，但是计算下沉量时误差被放大。实验中，下沉量小于6.8 mm的观测值时，相对误差大于5%。

(2)参考点个数的增加可以减小系统误差。系统误差随着参考点个数的增加在一定范围内波动，测量值误差的正负决定波动趋势。

(3)当参考点个数大于15时，误差均值向有序过渡，大于25时，表现为有序状态。为保证测量值的精度，至少需要25个参考点。

(4)研究可为保水开采覆岩移动变形规律和隔水层稳定性控制等模拟实验研究提供借鉴。

[1] 黄庆享.神府浅埋煤层的矿压特征与浅埋煤层定义[J].岩石力学与工程学报,2002,21(8):1174-1177. Huang Qingxiang.Ground pressure behavior and definition of shallow seams[J].Chinese Journal of Rock Mechanics and Engineering,2002,21(8):1174-1177.

[2] 范立民,马雄德,冀瑞君.西部生态脆弱矿区保水采煤研究与实践进展[J].煤炭学报,2015，40(8):1711-1717. Fang Limin,Ma Xiongde,Ji Ruijun.Progress in engineering practice of water-preserved coal mining in western eco-environment frangible area[J].Journal of China Coal Society,2015，40(8):1711-1717.

[3] 黄庆享.浅埋煤层覆岩隔水性与保水开采分类[J].岩石力学与工程学报,2010,29(2):3622-3627. Huang Qingxiang.Impermeability of overburden rock in shallow buried coal seam and classification of water conservation mining[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(2):3622-3627.

[4] 黄庆享,张文忠.浅埋煤层条带充填隔水岩组力学模型分析[J].煤炭学报,2015,40(5):973-978. Huang Qingxiang,Zhang Wenzhong.Mechanical model of water resisting strata group in shallow seam strip-filling mining[J].Journal of China Coal Society,2015,40(5):973-978.

[5] 黄庆享,赖锦琪.条带充填保水开采隔水岩组力学模型研究[J].采矿与安全工程学报,2016,33(4):592-596. Huang Qingxiang,Lai Jinqi.Study on mechanical model of aquifuge beam supported by filling strip in the water preserved mining[J].Journal of Mining & Safety Engineering,2016,33(4):592-596.

[6] 黄庆享.浅埋煤层保水开采隔水层稳定性的模拟研究[J].岩石力学与工程学报,2009,28(5):987-992. Huang Qingxiang.Simulation of clay aquifuge stability of water conservation mining in shallow-buried coal seam[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(5):987-992.

[7] 张杰,杨涛,田云鹏,等.采动及渗流作用下隔水土层破坏规律研究[J].岩土力学,2015,36(1):219-224. Zhang Jie,Yang Tao,Tian Yunpeng,et al.Experimental test for destruction law of aquiclude under action of mining and seepage[J].Rock and Soil Mechanics,2015,36(1):219-224.

[8] 黄庆享,张文忠,侯志成.固液耦合试验隔水层相似材料的研究[J].岩石力学与工程学报,2010,29(S1):2813-2818. Huang Qingxiang,Zhang Wenzhong,Hou Zhicheng.Study of simulation materials of aquifuge for solid-liquid coupling[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(S1):2813-2818.

[9] 黄庆享,侯志成,张文忠,等.黏土隔水层相似材料胶结剂的正交实验分析[J].采矿与安全工程学报,2007,24(1):42-46. Huang Qingxiang,Hou Zhicheng,Zhang Wenzhong,et al.Orthogonal tests on cementing agents of similar of clay aquiclude[J].Journal of Mining & Safety Engineering,2007,24(1):42-46.

[10] 黄庆享.浅埋煤层长壁开采顶板结构及岩层控制研究[M].徐州:中国矿业大学出版社,2000. Huang Qingxiang.Study on roof structrue and ground control in shallow seam longwall mining[M].Xuzhou:China University of Mining and Technology Press,2000.

[11] Luo Y.An improved influence function method for predicting subsidence caused by longwall mining operations in inclined coal seams[J].International Journal of Coal Science & Technology,2015,2(3):163-169.

[12] Hu Z,Chen C,Xiao W,et al.Surface movement and deformation characteristics due to high-intensive coal mining in the windy and sandy region[J].International Journal of Coal Science & Technology,2016,3(3):339-348.

[13] 李鸿昌.矿山压力的相似模拟试验[M].徐州:中国矿业大学出版社,1988. Li Hongchang.Similar simulation experiment of ground pressure[M].Xuzhou:China University of Mining & Technology Press,1988.

[14] 冯国瑞,任亚峰,王鲜霞,等.白家庄煤矿垮落法残采区上行开采相似模拟实验研究[J].煤炭学报,2011,36(4):544-550. Feng Guorui,Ren Yafeng,Wang Xianxia,et al.Experimental study on the upward mining of the left-over coal above gob areamined with caving method in Baijiazhuang Coal Mine[J].Journal of China Coal Society,2011,36(4):544-550.

[15] 冯国瑞,任亚峰,王鲜霞,等.采空区上覆煤层开采层间岩层移动变形实验研究[J].采矿与安全工程学报,2011,28(3):430-435. Feng Guorui,Ren Yafeng,Wang Xianxia,et al.Experimental study of the movement and deformation of rock strata between coal seam in the coal mining above gob area[J].Journal of Mining & Safety Engineering,2011,28(3):430-435.

[16] Kniel K,Härtig F,Osawa S,et al.Two highly accurate methods for pitch calibration[J].Measurement Science & Technology,2009,20(11):280-283.

[17] Sato Osamu,Osawa Sonko,Kondo Yohan,et al.Calibration and uncertainty evaluation of single pitch deviation by multiple-measurement technique[J].Precision Engineering,2010,34(1):156-163.

[18] 娄志峰,贺海钊,凌四营,等.齿距偏差测量中系统误差的分离方法[J].纳米技术与精密工程,2012,10(6):537-540. Lou Zhifeng,He Haizhao,Ling Siying,et al.Separation method of systematic errors in pitch deviation measurement[J].Nanotechnology and Precision Engineering,2012,10(6):537-540.

[19] 张毅,闫利,杨红,等.地面三维激光扫描的系统误差模型研究[J].测绘通报,2012(1):16-19. Zhang Yi,Yan Li,Yang Hong,et al.Research on systematic error model of terrestrial laser scanning[J].Bulletin of Surveying and Mapping,2012(1):16-19.

[20] 费业泰.误差理论与数据处理(第4版)[M].北京:机械工业出版社,2000. Fei Yetai.Error theory and data processing(4th edition)[M].Beijing:China Machine Press,2000.

Research on improving displacement measurement precision in physical simulation of water-preserved mining

ZHANG Yu-jiang1,2,FENG Guo-rui1,2,QI Ting-ye2,3,KANG Li-xun1,2,LUO Yi5,ZHANG Min2,4,YAN Yong-gan1,2

(1．CollegeofMiningEngineering，TaiyuanUniversityofTechnology，Taiyuan030024，China；2．ShanxiEngineeringResearchCenterforGreenMining，Taiyuan030024，China;3．InstituteofMiningTechnology,TaiyuanUniversityofTechnology,Taiyuan030024,China;4．CollegeofArchitectureandCivilEngineering，TaiyuanUniversityofTechnology，Taiyuan030024，China；5．DepartmentofMiningEngineering，WestVirginiaUniversity,Morgantown26506,USA)

Considering the wide-range and nonlinear characteristics of strata movement and the demand between large range and high precision in the physical simulation of water-preserved mining,a method for improving displacement measurement precision in physical modeling has been proved by experiments.The results show that the measurement accuracy is improved as the number of reference points and displacements increase.The increase of the number of reference points could reduce the system error which fluctuates in a range depending on the number of reference points and the fluctuation ascribes to the plus or minus of error.The mean error starts to reduce and diminish significantly when the number of reference points is 15 and 25 respectively.Therefore,at least 25 reference points are required to ensure the required precision.The method suggests a way for measuring strata movement in mining physical models.

physical simulation;strata movement;measurement accuracy;system error;water-preserved mining

10.13225/j.cnki.jccs.2016.5033

2016-10-03

2016-10-26责任编辑:许书阁

国家自然科学基金优秀青年科学基金资助项目(51422404)；国家自然科学基金面上基金资助项目(51574172)；山西省高等学校中青年拔尖创新人才资助项目

张玉江(1986—)，男，山东东营人，博士研究生。E-mail：ylczyj@yeah.net。通讯作者：冯国瑞(1976—)，男，山西阳城人，教授，博士生导师，博士。E-mail：fguorui@163.com

TD823

A

0253-9993(2017)01-0112-06

张玉江，冯国瑞，戚庭野，等.保水开采相似模拟高精度位移测量方法研究[J].煤炭学报,2017,42(1):112-117.

Zhang Yujiang,Feng Guorui,Qi Tingye,et al.Research on improving displacement measurement precision in physical simulation of water-preserved mining[J].Journal of China Coal Society,2017,42(1):112-117.doi:10.13225/j.cnki.jccs.2016.5033