多效蒸发脱硫液处理系统的设计及模型与优化

潘兆辉，陈迅，吴正松

(1.重庆大学三峡库区生态环境教育部重点实验室，重庆 400045；2.重庆屹唯新清洁技术有限公司，重庆 400084)

多效蒸发脱硫液处理系统的设计及模型与优化

潘兆辉1，陈迅2，吴正松1

(1.重庆大学三峡库区生态环境教育部重点实验室，重庆 400045；2.重庆屹唯新清洁技术有限公司，重庆 400084)

针对HPF脱硫工艺产生的副盐，设计了利用多效蒸发来处理脱硫废液的系统，节能环保效果显著。通过分析建立了系统的数学模型，为便于软件编程求解，用回归式来表示各相间的平衡关系；在此基础上，提出了系统的优化设计方法，以年费用为指标，采用拉格朗日乘子法和复合形法求解，并通过计算机实现其运算。最后以重钢为具体算例，求得最佳效数为1效，为其脱硫液处理系统设计及改进提供了理论参考。

脱硫液处理；多效蒸发系统；节能环保；数学模型；优化设计

氨法HPF焦炉煤气脱硫工艺因其碱源使用焦炉煤气中的氨而在焦化企业中得到了广泛运用。但该工艺会形成硫酸铵、硫代硫酸铵、硫氰酸铵等盐类[1]，而这些盐类的不断累积则会降低系统的脱硫效率[2]，甚至会堵塞脱硫塔。运用硫代硫酸盐与硫氰酸盐溶解度的差异，采取分步蒸发结晶法处理焦化脱硫废液，是国内目前较为成熟的方法[3]，但其能耗较大，国内外学者也一直在研发新的处理工艺。多效蒸发是节约蒸发所需生蒸汽非常有效的一个工艺，在轻工[4]、化工[5]、海水淡化[6]及食品工业[7]等行业中都已经得到了广泛应用，而在焦化行业尚处于科研探索阶段。针对国内焦化脱硫液处理现况，本文设计了低温多效蒸发焦化脱硫液处理系统，建立了系统的数学模型及优化设计模型，采用文献[8]、[9]的算法求解，并以重钢焦化厂为实例进行计算分析。

1 系统设计及模型

1.1 物理模型

根据脱硫废液的性质，蒸发器选用外热式多效组合型，为节约能耗、提高效率，还利用额外蒸汽来预热脱硫废液。

低温多效蒸发焦化脱硫废液处理系统设计如图1所示，由蒸发器、预热器、冷凝器以及旋液分离器组成。工艺流程如下：首先，脱硫废液进入第(n-1)个预热器，预热可以使脱硫废液具有很高的焓值，有效提高系统的换热效率。之后，脱硫废液自后向前依次进入各个预热器进行预热，结束预热阶段后进入系统的蒸发阶段。蒸发器中的蒸汽大部分作为下一效的加热蒸汽，剩余少量蒸汽作为预热器的热源；每效蒸发器中的溶液在旋液分离器进行分离，分离出的浓缩液送至下一效蒸发器进行再一次蒸发。

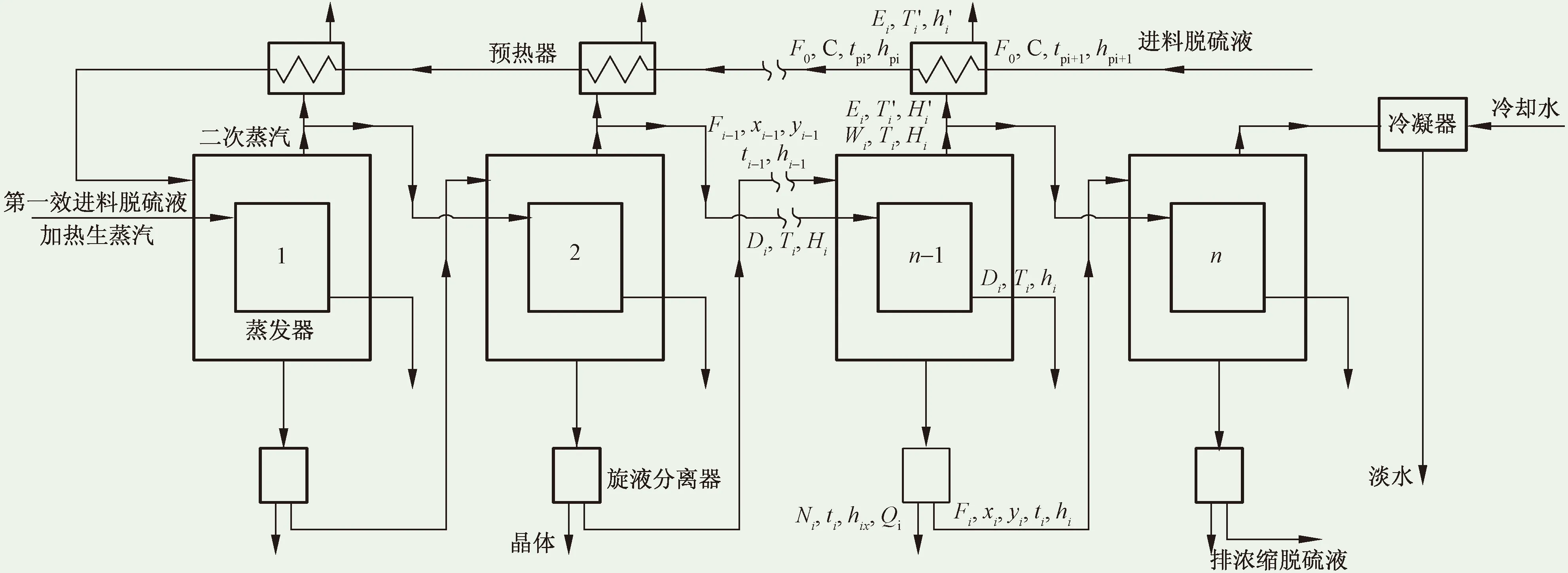
图1 低温多效蒸发焦化脱硫废液处理系统示意图Fig.1 Diagram of low-temperature multi-effect evaporation coking desulfurization wastewater treatment system

1.2 数学模型

1.2.1 系统物料衡算

由NH4SCN—(NH4)2S2O3—H2O的三相平衡图可知，蒸发器中析出的晶体为硫氰酸铵。假定溶质不挥发，结合文献[8]、[10]的方法得整个系统的物料衡算式：

(1)

(2)

式中，F0为初始脱硫废液(流入第1效，下同)的流量，kg/h；x0为初始脱硫废液中NH4SCN的初始浓度，%；y0为初始脱硫废液中(NH4)2S2O3的初始浓度，%；xi为第i效蒸发器流出的脱硫液中硫氰酸铵的浓度，%；yi为第i效蒸发器流出的脱硫液中硫代硫酸铵的浓度，%；Ni为第i效蒸发器析出的硫氰酸铵晶体量，kg/h；Wi为第i效蒸发器的蒸发水量，kg/h。

1.2.2 系统热量衡算

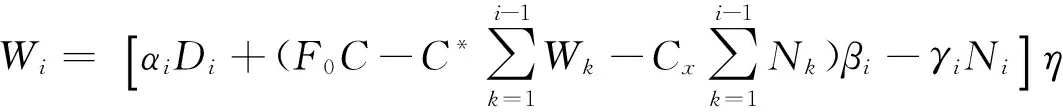
(3)

式中，Di为第i效加热蒸汽消耗量，kg/h；C为原脱硫液的比热，kJ/(kg(℃)；C*为水的比热，kJ/(kg(℃)；Cx为硫氰酸铵的比热，kJ/(kg(℃)；αi为第i效的蒸发系数；βi为第i效的自蒸发系数；γi为第i效硫氰酸铵固相析出系数；η为热利用系数，取0.98。

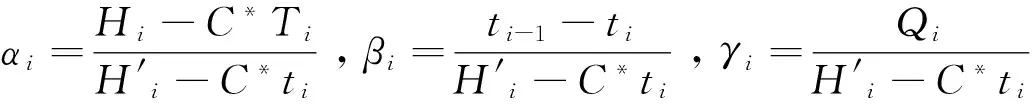
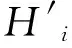
(2)对预热器(1≤i≤n-2)进行热平衡算得：

(4)

溶液的焓用比热计算，整理可得：

(5)

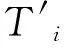
根据文献[12]，假设预热器的出口比该效二次蒸汽的入口温度低5℃，则有：

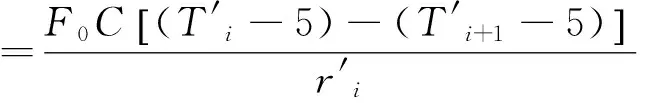
(6)

1.2.3 各效传热面积

依据传热速率方程[13]得各效蒸发器传热面积为：

(7)

式中，Si为第i效的传热面积，m2；Qi为第i效的传热速率，W；Ki为第i效的传热系数，W/(m2·℃)；Δti为第i效的传热温差，℃；ri为第i效加热蒸汽的汽化潜热，J/kg。

1.2.4 系统相平衡关系

(1)气液相平衡。计算各效蒸发系数、固相析出系数及传热温差等时需知该效溶液的沸点，可按照气液平衡方程[11]计算，即：

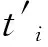
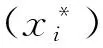
(8)

式中，yi为第i效中(NH4)2S2O3组分的浓度。

1.3 数学模型

计算求解多效蒸发系统，即联立各效物料、热量及相平衡等方程式，从而求出蒸汽用量(Di)、各效蒸发水量(Wi)、各效固相析出量(Ni)和各效浓缩液浓度(xi)等参数。实质上是求解一个非线性方程组，当系统效数和溶液组分较多时，求解会很烦琐。参考文献[11]中的迭代法结合矩阵法，其算法可通过计算机求解，收敛速度快，本文的算法步骤与其类似，故此仅讨论系统的物料和热量衡算式。

由1.2节所建立的数学模型可得各效蒸发水分量的计算式：

当i=1时，

(9)

当2≤i≤n-1时，

(10)

当i=n时，

(11)

系统总蒸发水量和固相析出总量的计算式：

(12)

系统中硫氰酸铵含量的物料衡算式：

(13)

将上述各式写成分块矩阵形式，其具体结构如下：

将矩阵方程式与传热速率方程式(1.7)及固液相平衡方程式(1.8)相联合，用迭代法结合矩阵法即可求出有固相析出的多效蒸发系统的全部参数。

2 系统优化设计

2.1 目标函数

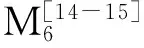
M=M1+M2+M3+M4+M5+M6

(14)

式中：

M1=3600×(a+bT0)·ξD1

(15)

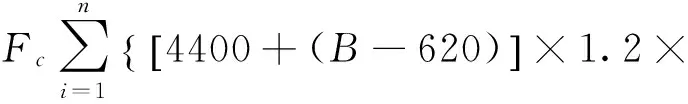
(16)

M3=M4=a·xb·f1·f2×1.3

(17)

(18)

(19)

式中，a、b(式15)分别为饱和蒸汽的价格系数；T0为生蒸汽饱和温度，℃；ξ为系统的运行时间，h/a；D1为初效蒸发器生蒸汽的用量，kg/s； Fc为蒸发器年折旧及维修率；B为市场钢材价格；Ai为第i效蒸发器传热面积，m2；hi为增资系数。式17中a、b为回归系数(式17)；x为换热器面积，m2；f1为压力校正系数；f2为材质校正系数；c1为凉水等动力费附加系数；c1为电费；Vw为水量，m3/s；ρ为水的密度，kg/m3；ηp为泵的效率；b0、b1、b2、b3为溶液输送泵回归系数；Ni为泵的轴功率，W。

上述各式中相关参数的说明及取值见参考文献[15]、[16]，而式19中的功率(Ni)除了管道输送液体消耗的功率[8]，还包括旋液分离器的功率[17]。

2.2 函数求解

分析目标函数M，可知其与M1和D1、T0有关，M2与Ai有关，而Ai又与Di和Δti有关，M3和M4与Ei有关，M5与Wn和Tk有关[15]，可以表示为：

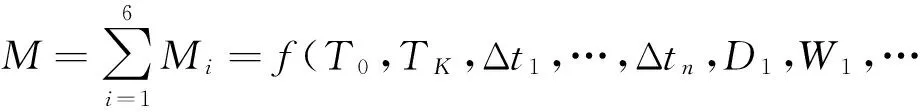
Wn，Ei，…，En-1，N1，…，Nn，x1，…，xn-1，y1，…，yn)

(20)

对n效蒸发器而言，函数M存在6n+1个变量。而相关的独立方程有5n-1个：溶质衡算式(求xi)有n-1个(xn是已知量)；溶解度方程式(求yi)共n个；各效蒸发水分量的方程式有n个；各效固相析出量烦人方程式n个；引出的额外蒸汽量的计算式共n-1个；总蒸发水分的量和固相析出总量的计算式1个。变量数减去方程数还有n+2个变量，即n效蒸发系统(有NH4SCN析出)的优化实质上是一个有约束的n+2维非线性规划问题，即：

minM=F(T0，TK，Δt1，…，Δtn)

(21)

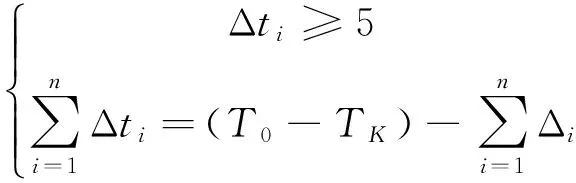
(22)

式(21)中,T0、TK的取值范围根据工程经验所定，各效传热温差(Δti)及总传热温差(ΣΔti)的约束由多效蒸发的特点而定[18]。因为目标函数M变量较多且约束条件复杂，本文采用复合形法结合拉格朗日乘子法来求解目标函数[15]。

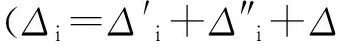
式中,b为常数(把ΣΔti视为不变)，引入拉格朗日的函数表达式，式19化为[8，15]：

M(Δt1，…，Δtn，λ)=M1+M3+M4+M5+M6+

式中，M1、M3、M4、M5、M6均与Δti无关，M2与Ai有关，而Ai则与Δti有关，把Ai=riDi/(ΔtiKi)代入式(22)，可得：

(24)

Si=1.2×0.0287[4400+(B-620)]hiFc

解式(24)得：

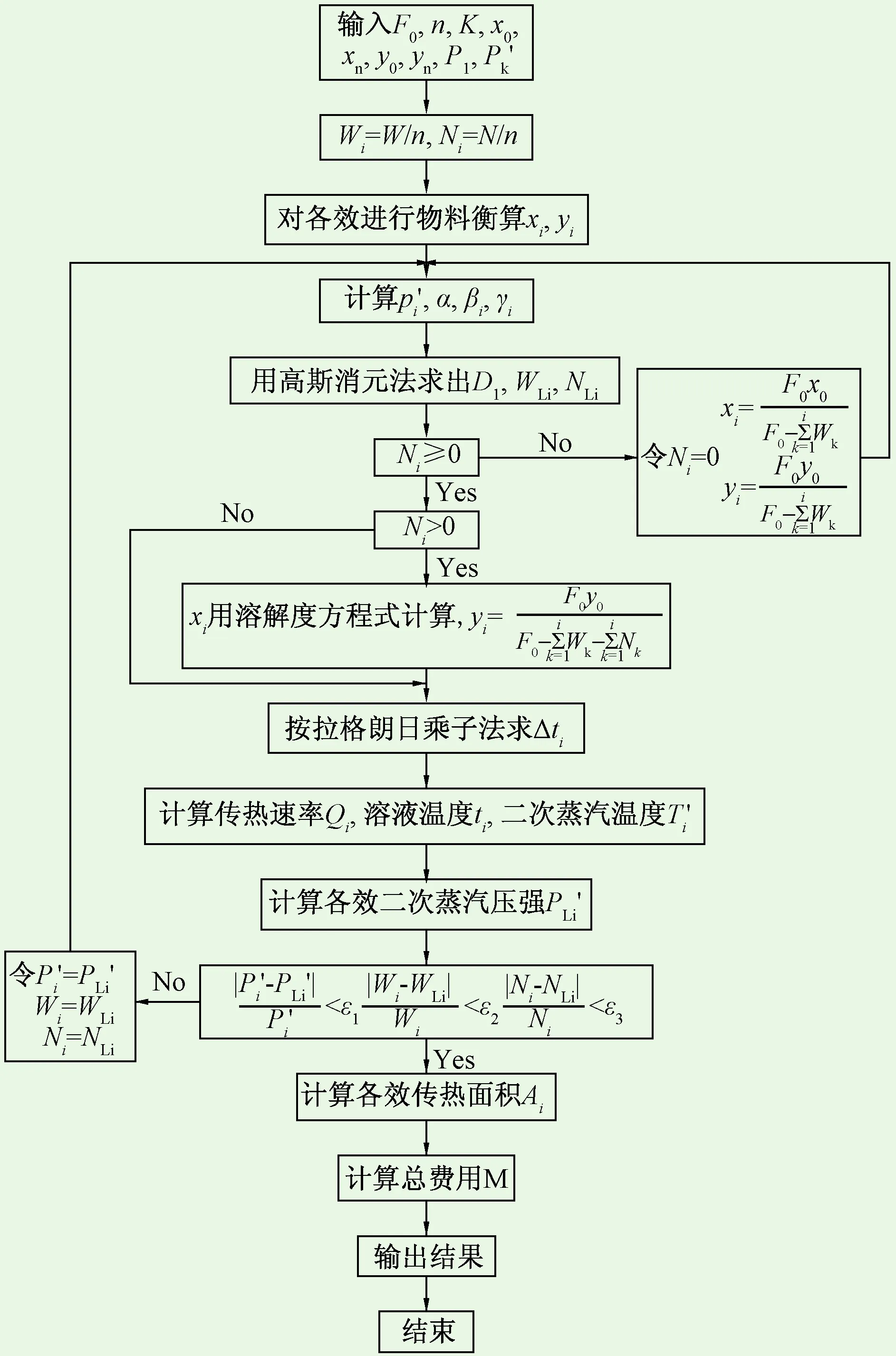
图2 系统优化计算流程图Fig.2 Flow chart of system optimization process

为了便于计算，选用功能强大的可视化语VisualBasic6.0编程实现其计算，软件操作界面人性化、计算精准可靠。计算流程如图2所示，ε1、ε2、ε3分别代表不同变量的收敛精度。

2.3 优化设计简要步骤

(1)根据经验,初选系统适用的3～4种效数方案,例如n=n1,n2,n3；

(2)对各个方案,分别求解minM；

(3)比较各方案的minM，最小的即为系统最优效数，还包括了系统的结构参数与热力学参数(各效)的确定。

3 计算实例

以重钢焦化厂的脱硫废液为数据来源，对本文设计的多效蒸发系统进行优化设计。焦化厂每天的脱硫废液是30 t，运行时长按20 h/d计算。焦化厂脱硫废液的初始温度为30℃，设计取初效蒸发器中蒸汽压力值为200 kPa，末效的冷凝器中压力为20 kPa。初始脱硫废液中硫氰酸铵的质量分数为37.2%，硫代硫酸钠的质量分数为2.6%，末效浓缩后分别为71%、14%。结果如图3所示：

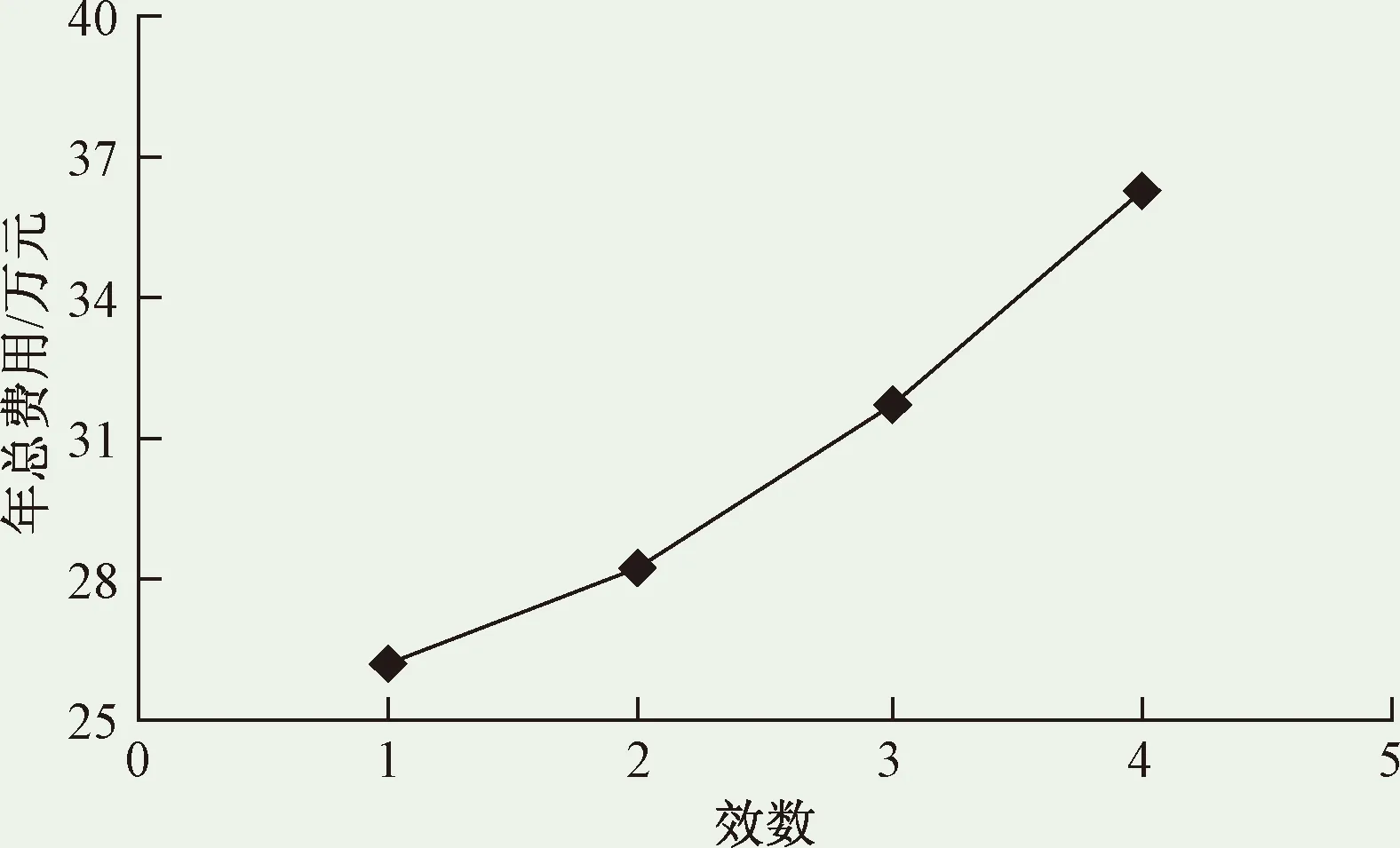
图3 不同效数脱硫废液处理系统的年费用Fig.3 Total cost of different effect numbers

由图3可知，随着效数的增加，蒸发系统的年总费用也相对增加，并且增长幅度也逐步增大，分析原因主要是每多设一效就需要增加相应一系列的设备。其次脱硫废液的量偏少，系统所需的蒸汽量也就很少，因此增加效数所减少蒸汽量的费用，远不能弥补其所增加设施的费用。

4 结论

(1)设计了低温多效蒸发焦化脱硫液系统，采取额外蒸汽预热脱硫废液等措施，具有显著节能效果。

(2)根据物料、热量衡算式及传热速率方程等，建立了系统的数学模型，用拟合式计算系统的汽液相和固液相平衡的溶解度方程，便于通过软件编程计算求解。采用矩阵法结合迭代法求解模型效率高、易收敛。

(3)选取系统年运行费用M作为优化比较的指标，建立了数学模型，通过复合形法结合拉格朗日乘子法可以有效地求解，且收敛快，算法稳定，具体计算可以通过功能强大的Visual Basic 6.0很好地实现。

(4)多效蒸发系统存在最佳效数，需要通过优化确定。以重钢焦化厂为例，确定其最佳效数为1效，此时年运行总费用M最省，为日后重钢焦化厂脱硫废液处理系统的设计及改进提供了理论参考。

[1] 陈新. 浅谈HPF工艺脱硫废液的处理[J]. 燃料与化工, 2010, 41(1): 53

[2] 曹密静. 新型络合铁脱硫剂的开发及脱硫工艺[D]. 唐山: 河北联合大学, 2013.

[3] 仵小录. 脱硫液副盐提取工艺技术方法探讨[J]. 山西化工, 2011, 31(5): 38.

[4] 阎尔平, 李忠国, 于守政, 等. YAR碱回收多效蒸发低碳节能热力系统的研究[J]. 纺织导报, 2016(2): 69- 71.

[5] 郝吉鹏. 6万吨/年NaOH碱多效蒸发系统的模拟与优化设计研究[D]. 成都: 西南石油大学, 2014.

[6] 陈军. 低温多效蒸发海水淡化系统的工艺流程模拟及优化[D]. 北京: 北京化工大学, 2013.

[7] 杨凯业. 制糖多效蒸发过程的模拟分析与改造[D]. 广州: 华南理工大学, 2015.

[8] 阮奇, 叶长燊, 陈文波, 等. 复杂逆流多效蒸发系统优化设计的模型与算法[J]. 化工学报, 2001, 52(8): 715- 720.

[9] 阮奇, 黄诗煌, 叶长燊, 等. 多效蒸发系统优化设计目标函数的建立与求解[J]. 计算机与应用科学, 2001, 18(1): 69- 75.

[10] 刘进荣. 有固相析出的多效顺流蒸发过程热量衡算[J]. 化工学报, 1994, 22(6): 55- 59.

[11] 方佳林, 阮奇, 李微, 等. 有固相析出的并流多效蒸发系统常规设计的模型和算法研究[J]. 四川大学学报(工程科学版), 2002, 34(5): 106- 110.

[12] 曹开智. 低温多效蒸发海水淡化变工况分析与实验研究[D]. 大连: 大连理工大学, 2006.

[13] 上海化工学院, 成都科技大学, 大连工学院. 化学工程(第1册)[M]. 北京: 化学工业出版社, 1980: 316- 352.

[14] 宋继田, 李丁, 叶京声, 等. 多效蒸发中最佳效数的确定[J]. 化工装备技术, 2002, 23(4): 25- 27.

[15] 李玲, 阮奇, 方佳林, 等. 有固相析出的并流多效蒸发系统优化设计研究[J]. 四川大学学报(工程科学版), 2002, 34(6): 61- 65.

[16] 葛维寰, 关淑, 王东平, 等. 化工过程设计与经济[M]. 上海: 上海科学技术出版社, 1987: 84- 86.

[17] L·斯瓦罗夫斯基. 固液分离[M]. 朱企新，译. 北京: 化学工业出版社, 1990: 183.

[18] 梁虎, 王黎, 朱平. 多效蒸发系统优化设计研究[J]. 化学工程, 1997, 25(6): 48- 51.

The Design, Modeling and Optimization Of Desulfurization Wastewater Treatment System by Multi-Effect Evaporation

PAN Zhao-hui1, CHEN Xun2, WU Zheng-song1

(1.Key Laboratory of Three Gorges Reservoir Region’s Eco-environment (Ministry of Education), Chongqing University, Chongqing 400045, China; 2.Chongqing Yiweixin Clean Technology Co., Ltd., Chongqing 400084, China)

For the by-product of HPF desulfurizing process, this paper designed a multi-effect evaporation system to treat desulfurization wastewater, which was effective in energy saving. It established the systematic mathematical model by analyzing, and correlating the equilibrium with equation so that the model could be easily solved by software. Based on this, the optimization design method was put forward. The indicator of the optimization design was the total annual cost of the system, and this model was solved by the Lagrangian multiplier method combined with the complex method, and was finally completed via computer software. In the end, this paper took Chongqing Iron and Steel Co., Ltd as a practical example, and pointed out according to the results that the optimal amount was 1, which provided a theoretical reference for the company.

desulfurization wastewater treatment; multi-effect evaporation system; energy saving; mathematical model; optimization design

2016-12-19

中央高校基金(106112014CDJZR210008)

潘兆辉(1989—)，男，硕士研究生，主要研究方向为废水处理理论与技术，E-mail：pandazhaohui@126.com

吴正松(1974—)，男，安徽庐江人，讲师，博士，主要研究方向为水环境保护及污泥的处理与处置，E-mail：zhswu2006@cqu.edu.cn

10.14068/j.ceia.2017.01.018

X703.1

A

2095-6444(2017)01-0074-06