考虑斜坡效应的桩柱式桥梁基桩稳定性分析
2017-02-20尹平保赵明华赵衡贺炜
尹平保+赵明华+赵衡+贺炜


长沙理工大学 桥梁结构安全控制湖南省工程实验室,湖南 长沙410114)摘要:考虑坡面以下一定深度范围内地基抗力非线性分布模式,建立了基桩稳定性分析简化计算模型及桩坡体系总势能方程.据此导得了斜坡段桩柱式桥梁基桩临界荷载与计算长度的能量法解答,并通过平地和斜坡两种不同情况下的室内模型试验验证理论计算方法的合理性.由此进行的参数分析表明:增大墩柱弹性模量或减小墩柱高度(高长比)均可提高基桩稳定性,当高长比取0.3~0.4时,基桩稳定性最佳;当边坡坡度在25°~35°范围内时,基桩稳定性受斜坡效应的影响较小,设计时应尽量将基桩设置在坡度小于35°的边坡上.斜坡段地基抗力比例系数m与坡度α之间的相互影响关系尚有待深入研究.
关键词:桥梁工程;基桩;稳定性;能量法;斜坡效应
中图分类号:TU473 文献标识码:AStability Analysis of Pilecolumn Bridge
of Bridge Structure (Changsha University of Science & Technology),Changsha,Hunan410114,China)Abstract:The soil resistance is a nonlinear function varying with depth, and it is related to the effect of location in slopes. The simplified model for a pilecolumn bridge pile and the total potential energy equation of pileslope system were presented by considering the slope effect. The analytical solution of the critical load and calculated length were derived based on the energy method. In this respect, verification between the measurement and theoretical solution was conducted by dissimilar conditions in plain and slope. The parametric study shows: the increase of the Young's modulus of the pier column or decrease of its free length enhances the stability of the pile foundation; the appointed elastic modulus of pier column corresponds to an optimal columnheight, and the best stability is achieved while the ratio is in the range of 0.3 to 0.4. Moreover, a key conclusion from observations is that the bridge pile should be located at the slope with the gradient less than 35° for safety. However, the correlation between m and α is of significance so that it needs to be further investigated.
Key words:bridge engineering;piles foundation;stability;energy method;slope effect
在西部山区修建桥梁工程,多采用桩柱式桥梁基桩,且往往将其设置在斜坡甚至悬崖峭壁上.与普通的桥梁基桩相比,位于斜坡上的桩柱式桥梁基桩具有坡度陡、墩柱高(普遍在30 m以上)等特点.因此,无论是受力分析还是稳定性计算,目前尚缺乏统一完善的技术标准或规定,给工程设计与施工带来极大不便,从而导致斜坡段桥梁基桩稳定性问题日益突出[1-3].
有关基桩稳定性问题,自20世纪60年代以来,国内外已有许多学者对其展开了一些有益研究,如:美国学者Lee(1968),利用钢管和铝管模拟基桩,进行了相应的室内模型试验研究[4];随后Reddy(1970)利用能量法对完全或部分入土桩的稳定性进行了理论研究[5].自20世纪90年代以来,国内学者赵明华(1990)、彭锡鼎(1996)、杨维好(2000)等,基于m法假定和能量原理,求解了不同边界条件下基桩屈曲能量方程,并得到了基桩屈曲临界荷载及稳定计算长度理论公式[6-8].近年来,郭红雨(2007)、Zou(2007)、姚文娟(2009)、张永兴(2010)等,从复杂地基抗力、初始弯矩和后屈曲等方面对基桩屈曲稳定性問题进行了深入的理论与数值分析研究[9-12].但针对斜坡上桩柱式桥梁基桩稳定性问题,目前国内外尚鲜有报道.
湖南大学学报(自然科学版)2016年第11期尹平保等:考虑斜坡效应的桩柱式桥梁基桩稳定性分析鉴于此,本文拟在现有研究的基础上,根据斜坡段桩柱式桥梁基桩的工程特点,考虑斜坡段桩前岩土体侧向约束弱化效应,建立相应的简化计算模型,并利用能量原理求解基桩临界荷载与计算长度,进而依托工程实例开展参数分析,以此探讨设计中的关键问题.
1斜坡效应分析
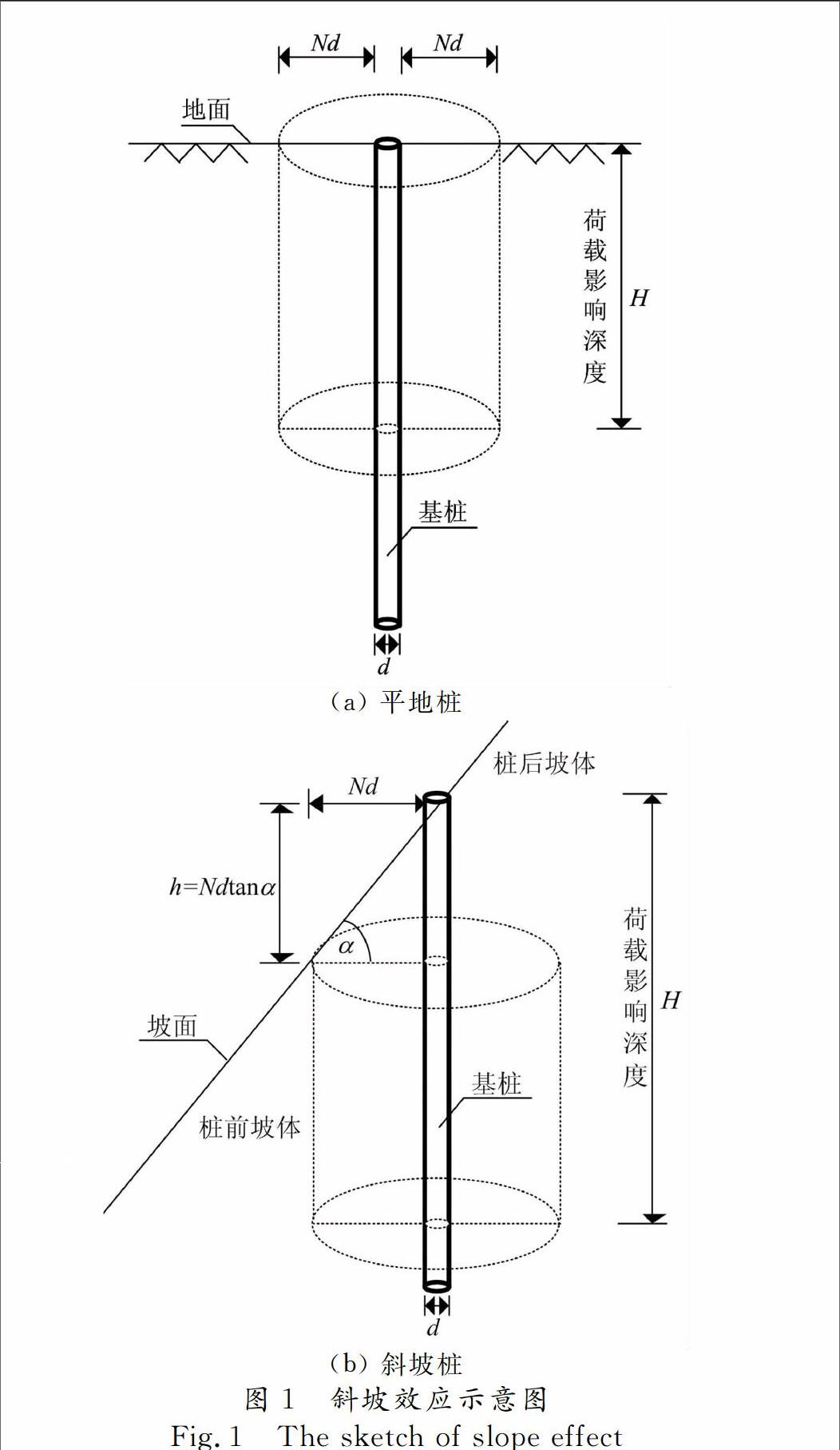
在各向同性、单层均质场地上,平地桩在任一截面均呈轴对称(图1(a)),且桩侧Nd范围内的岩土体均可提供有效的地基抗力;而斜坡段基桩(图1(b)),因桩前存在一临空面,使得基桩前、后岩土体不再对称,从而导致桩前Nd(距桩顶h=Ndtanα)范围内岩土体所能提供的地基抗力与平地桩相比明显减弱.这种因斜坡存在而导致的桩前岩土体地基抗力弱化现象称为斜坡效应.其中,h=Ndtanα为斜坡效应影响深度;Nd为斜坡效应影响宽度;d为桩径;N为斜坡效应系数,一般可取3~5[13].
(a) 平地桩
(b) 斜坡桩
2方程建立与求解
2.1基本假定
为建立斜坡段桩柱式桥梁基桩稳定性分析模型,据其承载状况、边界条件等,特作如下假定:
1) 山区斜坡段桩柱式桥梁基桩一般都为嵌岩桩,即可假定桩底为完全固定约束.通常情况下,桩顶主要包含自由、弹嵌、嵌固和铰支4种约束.对于桥梁基桩,其桩顶往往受盖梁、支座等弹性约束,并非完全自由或嵌固,故可假定为弹嵌.据此可假定“桩底嵌固,桩顶弹嵌”边界下基桩挠曲变形函数为[6]:
x=∑ni=1ci1-cos iπlz (1)
式中:x为桩身水平位移;z为计算点至桩底的距离(坐标原点设在桩底中心);ci为待定系数;l为基桩总长;n为半波数;
2) 假定基桩仅发生平面内运动,即不考虑基桩空间上的弯扭或转动,且桩身各截面沿横向始终保持为一完整平面,并与纵向垂直[6];
3) 忽略桩身自重、桩侧摩阻力对基桩屈曲稳定性的影响[14];
4) 为考虑斜坡效应,根据m法假定h深度范围内桩侧地基抗力系数沿深度呈非线性发展,则桩侧地基抗力p(x, z)表达式为:
p(x,z)=C(z)b1x=mf(z)b1x=
mH-z2hb1x H-h mH-h-zb1x 0 式中:p(x, z)为桩侧地基抗力;m为地基抗力比例系数;b1为桩身计算宽度;H为基桩入土深度; C(z)为桩侧地基抗力系数,其在h深度内的变化发展模式如图2所示,式中其他参数同前. 2.2计算模型 根据上述分析可建立考虑斜坡效应的桩柱式桥梁基桩稳定性分析简化计算模型,如图3所示. 在图3所示的计算模型中,将桩柱式桥梁基桩分为3段(总长l= l1+ l2+ l3):嵌固段(l1)、斜坡效应影响段(l2)以及墩柱段(l3),其中l2=h=Ndtanα,α为边坡坡度;E2I2为墩柱抗弯刚度;E1I1为基桩抗弯刚度;P为桩顶竖向荷载;坐标原点定为桩底中心. 2.3总势能方程的建立 首先建立桩坡体系总势能方程.由图3可知,桩坡体系的总势能P应由基桩弯曲应变能Up、桩侧岩土体弹性变形能Us以及桩顶竖向荷载势能Vp组成[6]: Π=Up+Us+Vp (3) 基桩弯曲变形产生的应变势能Up为[6]: Up=E1I12∫H0(x'')2dz+E2I22∫lH(x″)2dz (4) 式中:H= l1+ l2,x′,x″分别为挠曲变形函数x的一、二阶导数,式中其他参数同前. 桩侧岩土体弹性变形能Us为[6]: Us=12∫H0p(x,z)xdz(5) 桩顶竖向荷载势能Vp为[6]: Vp=-12P∫l0(x')2dz(6) 从而可得桩坡体系总势能方程为: ∏=E1I12∫H0(x″)2dz+E2I22∫lH(x″)2dz +12∫H0p(x,z)xdz-P2∫l0(x′)2dz (7) 2.4能量法解答 將式(1)及其一、二阶导数、式(2)代入式(7),积分后整理可得: ∏=E1I1-E2I2)π44l4Φ(A)+mb1(Hh-H2)2hΦ(B)- mb1(h+2H)2hΦ(D)+bm1H22hΦ(E)+mb1HhΦ(F)+ mb12h[Φ(G)-Φ(J)]+E2I2π44l4-Pπ24l∑ni=1c2ii2(8) 式(8)中的Φ(χ)函数表达式为: Φ(χ)=∑ni=1c2iχii+∑ni=1∑nj=1j≠icicjχij(9) 式中:χ=A,B,D,E,F,G,J;χii,χij为与d,α,l,h,H,i(i=1,2,…,n),j(j=1,2,…,n)等有关的系数. 对式(8)取变分,并令∏ci=0,可得: (Kii-X)ci+Kijcj=0 (10) 式中:P=π2EIl2X;EI=E1I1H+E2I2(l-H)l; Kii=4l3π4EIiπ44l4E1I1Aii-E2I2Aii+E2I2i4+ mb1(hH-H2)2hBii-Dii+mb1H2hHEii-2Fii+ mb1H2hGii-Jii Kij=4l3π4EIiπ44l4E1I1-E2I2Aij+ mb1H(h-H)2hBij+mb1(2H-h)2hDij+ mb1H2h(HEij-2Fij)+mb12hGij-Jij 式(10)可写成矩阵方程形式: KC=0 (11) 式(11)中含有n个变量ci(i=1, 2, 3, …,n),要使其具有非零解,则其系数行列式必为零,即: K=0 (12) 式(12)即为基桩稳定性分析的特征方程. 根据式(12)可求得n个特征根,设其最小正根为Xmin,则基桩临界荷载Pcr和计算长度Lcr为: Pcr=π2EIl2Xmin (13) Lcr=lXmin (14) 3试验验证 3.1试验1 为验证计算方法的可靠性,以文献[14]中的试验桩为例进行对比分析.计算时取边坡坡度α=0,从而将斜坡桩退化为平地桩,并取n=30,其他参数取值与文献[14]中的试验参数相同(见表1),具体计算结果如表2所示.
由表2可以看出,理论计算结果与试验实测结果吻合较好(最大误差不足10%),验证了本文计算方法的可行性.上述计算过程可通过编制相关的MATLAB程序实现求解.
3.2试验2
以张(家界)—花(垣)高速公路中的某实际工程桩为原型,开展了不同坡度下基桩竖向承载室内模型试验,如图4所示.该模型试验采用PPR管模拟基桩,采用不均匀系数为Cu=8.57,曲率系数Cc=1.05的粗砂模拟桩周土体.模型基桩外径d1=63 mm,内径d2=58 mm.桩长l=1 200 mm,其中埋入坡体中的长度H=800 mm;桩身弹性模量E=1 680 MPa.实测桩侧地基抗力系数、基桩竖向屈曲临界荷载Pcr以及理论计算结果如表3所示.
由表3可以看出,理论计算结果与室内模型试验结果相差不大,60°斜坡基桩的计算误差达9.68%,这是因为实际情况中的地基抗力比例系数m值随斜坡坡度呈非线性变化,从而造成理论计算模型假定与实际情况有一定差别.
4工程实例分析
张(家界)—花(垣)高速公路某桥梁采用桩柱式基础,基桩所在边坡坡度α=30o~50o;基桩长H=25.0 m;基桩直径d1=2.0 m;墩柱高l3=8.0 m;墩柱直径d2=1.8 m.基桩采用C25混凝土,其弹性模量E1=28 GPa;墩柱采用C30混凝土,其弹性模量E2=30 GPa;桩侧地基抗力比例系数m=60 MN/m4;n=30;N=5;基桩竖向设计荷载Pst=6 519 kN.以该基桩为例,重点分析墩柱弹性模量E2、高长比l3/l(墩柱高度l3与基桩总长l之比)以及边坡坡度α对基桩稳定性的影响.
保持其他参数不变,仅改变墩柱弹性模量E2值(0.6E2,0.8E2,1.0E2,1.2E2)计算得到不同E2下基桩无量纲临界荷载cr,无量纲计算长度cr与高长比l3/l间的关系曲线,见图5和图6.
高长比l3/l
由图5可知,当高长比l3/l相同时,增大墩柱弹性模量E2,基桩临界荷载值随之增大,此与文献[14]所得结论完全吻合.但当墩柱弹性模量E2相同时,随高长比l3/l增加,基桩临界荷载随之先小幅增大,后急剧减小.这是因为基桩整体刚度EI=[E1I1H+E2I2(l-H)]/l受墩柱弹性模量E2和长度l3共同影响,即:E2增大,导致EI增大,cr值增加,有利于基桩稳定;若增大l3(总长l变大),将导致EI减小,cr值减小,对基桩稳定不利.另外,从图5和图6还可以发现,当高长比取0.3~0.4时,基桩稳定性最佳.由图5和图7可知,不同E2对应的cr-l3/l、cr-cr关系曲线均出现一峰值点,这表明桩身材料刚度与最佳桩长(或最优高长比l3/l)存在一一对应关系,据此可对斜坡段桩柱式桥梁基桩进行优化设计.
无量纲计算长度
由图8可以发现,当墩柱高度相同时,边坡坡度正切值tanα越大,基桩无量纲临界荷载值cr(右边纵坐标,空心圆点),先急剧减小,再缓慢减小,然后又急剧减小;而基桩无量纲计算长度值cr(左侧纵坐标,实心方点)则与之相反,这说明边坡坡度对基桩稳定性的影响非常显著.当0.45
將基桩竖向设计荷载及桩长无量纲化,可得其无量纲设计荷载st=0.0068,无量纲设计桩长st=12.87.再结合图8可得最不利状况(坡度α=50o,tanα=1.19)下基桩无量纲临界荷载cr=0.027,无量纲计算长度cr=8.47.二者比值分别为:cr/st=3.97,st/cr=1.52.由此可见,基桩竖向承载稳定性满足要求;目前该桥梁已建成通车,施工及运行期间均未现安全隐患.
5结论
首先根据斜坡段桩柱式桥梁基桩承载特性,建立了考虑斜坡效应的基桩稳定性分析简化计算模型;然后利用能量原理导得了基桩临界荷载与计算长度公式,并通过算例验证其可行性;最后以某实际工程为例开展参数分析得到如下结论:
1) 增大墩柱刚度或减小墩柱高度均可提高基桩稳定性;高长比为0.3~0.4时,基桩稳定性最佳.对斜坡基桩,可根据墩柱弹性模量与最优高长比之间的关系确定最合理的桩材和桩长;
2) 边坡坡度对基桩稳定性的影响非常明显,当边坡坡度在25°~35°(0.45 3) 有关斜坡段地基抗力比例系数m与斜坡坡度之间的相互影响关系尚有待开展相应的试验研究. 参考文献 [1]邹新军, 陈少玉, 尹帮顺, 等. 基桩动力稳定性模型试验研究[J]. 湖南大学学报:自然科学版, 2012, 39(12): 19-24. ZOUZ Xinjun, CHEN Shaoyu, YIN Bangshun, et al. Model test for dynamic stability of piles[J]. Journal of Hunan University:Natural Sciences, 2012, 39(12): 19-24. (In Chinese) [2]张永杰, 李侑军, 赵明华, 等. 高陡斜坡作用下群桩基础设计计算方法[J]. 中国公路学报, 2014, 27(10): 84-92. ZHANG Yongjie, LI Youjun, ZHAO Minghua, et al. Design and calculation method for pile group foundation in high and steep slope[J]. China Journal of Highway and Transport, 2014, 27(10): 84-92. (In Chinese)
[3]尹平保, 赵明华, 杨明辉, 等. 考虑PΔ效应的陡坡段桥梁双桩结构受力分析[J]. 湖南大学学报:自然科学版, 2012, 39(1): 1-6.
YIN Pingbao, ZHAO Minghua, YANG Minghui, et al. Force analysis of bridge doublepile in high and steep slope with consideration of PΔ effect[J]. Journal of Hunan University:Natural Sciences, 2012, 39(1): 1-6. (In Chinese)
[4]LEE K L. Buckling of partially embedded piles in sand[J]. Journal of Soil Mechanics and Foundation Division, ASCE, 1968, 94(1): 255-270.
[5]REDDY A S, VALSANGKAR A J. Buckling of fully and partially embedded piles[J]. Journal of Soil Mechanics and Foundation Division, ASCE, 1970, 96(6): 1951-1965.
[6]赵明华. 桥梁桩基的屈曲分析及试验[J]. 中国公路学报, 1990, 3(4): 47-57.
ZHAO Minghua. Buckling analysis and tests of bridge piles[J]. China Journal of Highway and Transport, 1990, 3(4): 47-57. (In Chinese)
[7]彭锡鼎. 考虑桩侧土壤弹性抗力时桩的临界荷载计算[J]. 土木工程学报, 1996, 29(5): 43-48.
PENG Xiding. Calculation of critical load of pile considering resistance of soil on the side of pile[J]. China Civil Engineering Journal, 1996, 29(5): 43-48. (In Chinese)
[8]杨维好, 任彦龙. 端部嵌固桩的稳定性分析[J]. 岩石力学与工程学报, 2000,19(3): 380-382.
YANG Weihao, REN Yanlong. Axial buckling analysis of bottomfixed pile[J]. Chinese Journal of Rock Mechanics and Engineering, 2000,19(3): 380-382. (In Chinese)
[9]郭红雨, 贾艳敏. 用能量法确定考虑冻胀力和冻土抗力作用时桩基的临界荷载[J]. 工程力学, 2007, 24(7): 167-173.
GUO Hongyu, JIA Yanmin. Determination of critical loads for piles by energy method considering frost heave forces and resistance to deformation of frozen soil[J]. Engineering Mechanics, 2007, 24(7): 167-173. (In Chinese)
[10]ZOU Xinjun, ZHAO Minghua, LIU Guangdong. Buckling analysis of superlong rocksocketed filling piles in soft soil area by element free Galerkin method [J]. Journal of Central South University, 2007,14(6): 858-863.
[11]姚文娟, 仇元忠, 程泽坤. 超长嵌岩桩初始后屈曲性状分析[J]. 岩土工程学报, 2009, 31(5): 738-742.
YAO Wenjuan, QIUYuanzhong, CHENG Zekun. Initial postbuckling analysis for superlong rocksocketed piles[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(5): 738-742. (In Chinese)
[12]张永兴, 陈林, 吴曙光. 基于Wieghardt地基桩基稳定性分析[J]. 岩土工程学报, 2010, 32(S2): 9-12.
ZHANG Yongxing, CHEN Lin, WU Shuguang. Stability analysis of pile on a Wieghardttype elastic foundation[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(S2): 9-12. ( In Chinese)
[13]趙明华, 刘涛, 杨超炜, 等. 考虑陡坡效应的横向受荷桩受力分析纽玛克解答[J]. 公路交通科技, 2014, 31(10): 58-64.