论小学数学概念的教学

曾朝晖

摘 要： 小学数学概念是数学基础知识的重要组成部分，是学习其他数学知识的基础。因此数学概念教学是课堂教学的重中之重。让学生易学、易懂、易运用是教学的关键，而要做到这一点，应从以下五方面入手：以感性材料促具体与抽象的转化；用对比与类比辨别概念的差异；剖析关键词语，深化概念理解；以新旧概念联系促进知识的迁移；运用于生活实践，实现概念的升华。

关键词： 数学概念 转化 对比 迁移 运用

数学概念是客观现实中的数量关系和空间形式的本质属性在人脑中的反映。新课标指出我们要让学生经历观察、实验、猜想、证明等数学活动，发展合情推理能力和初步演绎推理能力。学习数学知识的过程就是一个不断运用已有数学概念进行比较、分析、综合、概括、判断和推理的思维过程。由此可见，小学数学是一门概念性很强的学科，数学概念不仅是数学基础知识的重要组成部分，而且是学习其他数学知识的基础。因此，任何一部分内容教学都离不开概念教学，直接关系数学知识的理解与运用。所以为了充分激发学生的学习热情，更好地让学生掌握知识，实现教学目标，小学数学概念教学应从以下五方面入手。

一、以感性材料促具体与抽象的转化

在小学教材中由于数学概念的抽象性与学生思维的形象性的矛盾，要让学生更好地理解概念，必须从学生了解的实际事例或已有知识经验出发，通过学生在日常生活中接触到的事物或教材中的实际问题及模型、图形、图表等感性材料让学生观察，在观察的基础上通过教师的启发引导，对感性材料进行比较、分析、综合，最后抽象概括出概念的本质属性。

例如：“圆周率”是一个非常抽象的概念，我在课前让每个学生用硬纸板制作一个圆，不限定半径。课堂上，让每个学生在课堂练习本上写出三个内容：（一）写出自己要做的圆的直径；（二）滚动自己的圆纸板，量出圆滚动一周的长度，写在练习本上；（三）计算圆的周长是直径的几倍。全班学生做完后，汇报自己计算的结果，并把结果整理成下表：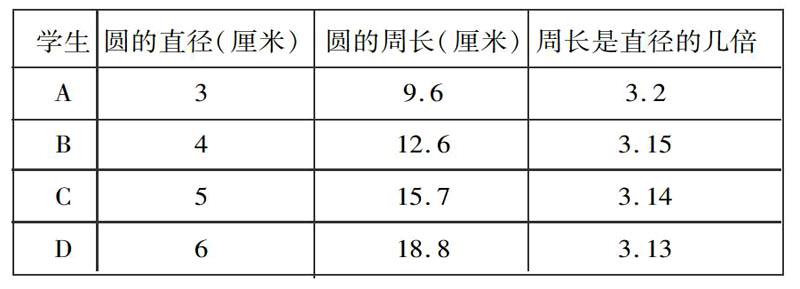

引导学生分析发现：不管哪个圆，它的周长总是直径的3倍多一些。这时候揭示：这个倍数是个固定的数，数学上叫做圆周率。然后让学生再画一个圆，量出直径和周长加以验证。这样教师借助于直观教学，运用学生原有的基础知识，加以分析、综合、抽象、概括，环环紧扣、层次清楚，通过实物演示建立表象，解决数学概念的抽象性与儿童思维形象性的矛盾，抓住事物的本质特征形成概念。

二、用对比与类比辨别概念的差异

在小学数学概念中有些含义非常接近，却有本质属性的差别，学生常常容易混淆，必须通过对比，找出概念间的相同和不同之处，以避免互相干扰。

例如：在学习“整除”时，为了和以前学习的“除尽”加以比较。我设计了这样的练习题：下列等式中，哪些是整除，哪些是除尽？

（一）9÷3=3 （二）24÷6=4

（三）49÷11=4······5 （四）12÷5=2.4

（五）4÷0.5=8 （六）3.5÷7=0.5

学生通过分析、比较，从而得出：第（三）题是有余数的除法，肯定不能说被除数整除或除尽，其他各题都可以说被除数除尽。而只有第（一）（二）题被除数、除数和商都是整数，而且没有余数，这两题不但可以说被除数除尽，还可以说被除数整除。通过分析，学生明白：整除是除尽的一种特殊形式，除尽包括整除和一切商是有限小数的情况。

三、剖析关键词语，深化概念理解

理解概念的目的在于运用，而要学生正确、灵活地运用概念就必须正确、灵活地运用概念的组成判断，进行推理、计算等，而概念是几个关键词语的高度概括和集中体现，因此剖析概念中的关键词语是概念教学的重中之重。

例如：循环小数定义中的“小数部分”、“依次”、“不断”、“重复”，学生只有清楚这些关键词语的真实含义，才会对循环小数的概念有深刻的理解。又如三角形的高的定义：“从三角形的一个顶点到它的对边作一条垂线，顶点和垂足之间的线段叫做三角形的高，这条也叫做三角形的底。”这里的“一个顶点”、“垂线”、“垂足”都是关键词语。为了更好地让学生理解三角形的高，除了让学生理解字面意思外，还要学生通过实际操作，体会画“高”的整个过程。指出画“高”的关键是画垂线，并注意限制条件：“过三角形的一个顶点（可以是任何一个顶点），作它对边的垂线，顶点和垂足之间的线段。”这样把实际操作过程和所画三角形高的图形与定义叙述的内容对照，使学生准确理解三角形高的定义。所以对重点词语的分析是帮助学生认识概念的又一次提高，促进概念的深化理解。

四、以新旧概念联系促进知识的迁移

小学生的认识特点是由浅入深、由易到难、循序渐进。为了加强数学概念教学，教师必须认真钻研教材，掌握概念的系统，摸清概念发展的脉络。概念是逐步发展的，而且很多概念之间有密切的联系。不同概念具体要求不同，即使同一概念在不同的学习阶段的要求也是有所差别的。为了让学生更好地掌握概念，必须加强新、旧知识的联系，促进知识的迁移。

例如：对分数意义的理解上有三次飞跃。第一次是学习小数以前，就让学生初步认识分数，“像上面讲的1/2、7/8、3/5、4/9等，都是分数”。通过大量直观感性认识，结合具体事物的描述得出什么样的数是分数，初步理解分数是平均分得到的，理解谁是谁的几分之几。第二次飞跃是由具体到抽象，把单位“1”平均分成若干份，表示其中一份或几份都可以用分数表示。从具体事物中抽象出来，然后概括分数的定义，这只是描述性地给出了分数的概念，这是感性的飞跃。第三次飞跃是对单位“1”的理解与扩展，单位“1”不仅可以表示一个物体、一个图形、一个计量单位，还可以是一个群体等，最后抽象出把谁分谁就是单位“1”，这样单位“1”与自然数“1”的区别就更明确。这三个层次不是一蹴而就的，要展现知识发展过程，引导学生在知识的发生发展过程中理解分数。

五、運用于生活实践，实现概念的升华

从生活中来，到生活中去是数学的最好体现。所以学生学习数学不能仅停留在理解和掌握知识的层面上，必须学会运用才会使学生学到的概念巩固下来。只有这样，才能使所学数学富有生命力，才能真正体现数学的价值。

例如：在学习圆的面积后，我设计了这样一个问题：“同学们已经学习了圆的面积公式，谁能算出我们学校东北角那棵大柳树的横截面面积？”学生议论纷纷，有的说，算圆面积一定要知道半径，只有把树砍下来才能量出半径；有的反对这样做，认为树一砍下来就会死掉。这时进一步引导说：“能不能不砍树就算出了树的横截面积呢？大家再讨论一下。”一石激起千层浪。学生通过积极思考和争论，终于找到好办法：先量出树干的周长，再算出半径，从而应用面积公式算出大树横截面的面积。课后许多学生还到操场上实际测量树干的周长，算出横截面的面积。这样通过创设有效的教学情境，进行适时的点拨，不但启发学生的思维，而且培养学生学以致用的兴趣和能力，加深对所学概念的理解。

总之，概念教学是一门科学，也是一门艺术，要根据小学生的心理特点和认知规律，充分发挥教师的主导和学生的主体作用，精心设计练习，巩固和深化概念的理解和掌握，重视概念系统的建立，引导学生形成良好的认知结构，从而体现数学概念是数学知识的基石，使概念教学真正成为培养学生数学能力的前提和保证。

参考文献：

[1]张思碧.谈小学数学概念的教学方法[OL].龙源期刊网，2009-7-6.

[2]冀冬云.浅谈小学数学概念教学的方法[OL].中国知网，1998-9-15.