基于RBF神经网络和单神经元PID的PMSM速度控制器

绵阳市维博电子有限责任公司 宋永强中国兵器装备集团自动化研究所 刘议聪绵阳市维博电子有限责任公司 朱泓光

基于RBF神经网络和单神经元PID的PMSM速度控制器

绵阳市维博电子有限责任公司 宋永强
中国兵器装备集团自动化研究所 刘议聪
绵阳市维博电子有限责任公司 朱泓光

为提高PMSM(Permanent Magnet Synchronous Motor,永磁同步电机)伺服系统的控制水平，本文提出一种基于RBF(Radial Basis Function,径向基函数)神经网络和单神经元PID的PMSM速度控制器,可根据PMSM伺服系统的实时状态进行速度控制器内部参数自整定，由于具备这种能力，使PMSM伺服系统的速度环实现全局最优控制。实际中，工业过程控制对平稳度要求较高，针对此要求对单神经元PID算法进行改进，将固定比例系数改进为跟随系统误差变化的变比例系数，这种改进有效的减少了系统超调，使控制更加平稳。

PMSM；RBF神经网络；单神经单元PID控制器

0 引言

PMSM(Permanent Magnet Synchronous Motor，永磁同步电机)伺服系统的发展，满足了日趋复杂的工业过程控制。如何提高PMSM伺服系统的性能一直是人们关注的焦点，而PMSM伺服系统大多使用传统的PID控制器，伺服系统的性能取决于PID参数的匹配程度。因PMSM为多变量、非线性、强耦合、参数时变系统，所以很难找到一组PID参数能使系统达到较为理想的控制水平。一般控制过程存在较多的状态，传统的PID控制器只能实现局部最优，而不能兼顾所有状态。目前，智能控制策略已经成功应用于PMSM伺服系统控制，以解决传统PID控制器的不足。基于前向多层神经网络的PID自整定算法用于PMSM伺服控制系统的研究较多。这类研究一般是通过前向神经网络对伺服系统进行辨识，利用辨识结果对PID控制器参数进行整定以达到控制效果。

在PMSM的智能控制领域，也有使用单神经元PID算法直接作为伺服系统三环控制器的研究。本文提出一种将RBF多层神经网络和单神经元PID控制器相结合的算法，通过RBF神经网络辨识器对单神经元PID控制器的连接权值进行调整，利用此算法对PMSM伺服系统的速度环进行控制，可大大提高PMSM伺服系统的控制水平。

进一步，本文对单神经元PID控制器的比例系数K进行改进，改进后的速度控制器可使PMSM伺服系统获得更好的抗扰能力，且控制性能更加平稳。

1 基于矢量控制的PMSM模型

1.1 PMSM数学模型

PMSM在d、q旋转坐标系下的数学模型可表示如下：

（1）电压方程

上式中，ud、uq为d、q轴的定子电压(V)，id、iq为d、q轴的定子电流(A)，Ld、Lq为定子绕组在d、q轴上的等效自感(H)，ψf为转子永磁体磁链(Wb)，ω为电机的电角速度(rad/s)。

（2）电磁转矩方程

上式中，Pn为PMSM的极对数，Pniqψf为永磁体在q轴产生的永磁转矩，(Ld－Lq)idiq为由于转子的凸极效应产生的磁阻转矩。

（3）电机运动方程

上式中，JM为PMSM的转动惯量，B为转子等效阻尼系数，ωm为机械角，T为伺服拖动系统的负载转矩。

1.2 PMSM矢量控制

当使用id=0控制时，PMSM在d、q坐标系下的数学模型可以进一步简化为：

（1）电压方程

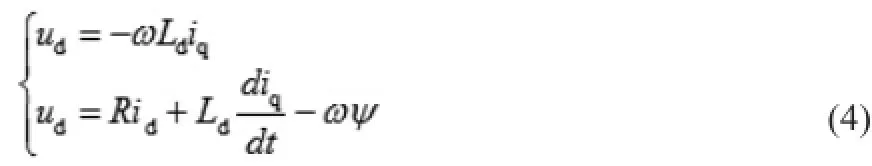
（2）电磁转矩方程

（3）电机运动方程

控制系统结构如图1所示，控制原理为：速度给定ωr与实际速度的差值Δω为速度控制器的输入，速度控制器产生转矩电iq*。通过PARK变换，把逆变器输出给PMSM的三相定子电流变换为两项旋转坐标系下的电流id、iq。转矩电流信号iq*、励磁电流信号id*和实际电流id、iq经过电流控制器的比较计算得到相应的电压信号ud*、uq*。利用PARK逆变换对d、q轴电压信号进行变换，继而得到a、b、c三相坐标系的电压指令信号，再通过SVPWM的调制产生控制逆变器的脉宽调制信号，从而驱动PMSM。

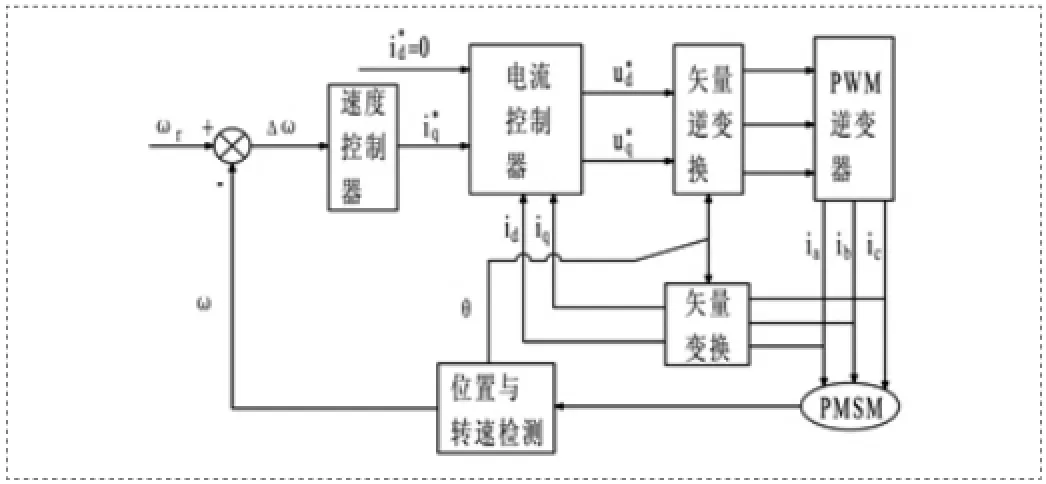
图1 PMSM矢量控制系统结构图

2 RBF神经网络辨识器

RBF (Radial Basis Function，径向基函数)神经网络是一种3层前向网络，虽然输入到输出的映射是非线性的，而隐层空间到输出空间的映射却是线性的，且RBF神经网络是局部逼近的网络，因此采用RBF神经网络即可大大加快学习速度，又能避免局部极小问题[1]。

本文使用具有3个输入节点和6个隐层节点的RBF神经网络作为PMSM伺服系统的辨识器，拓扑图如图2所示。

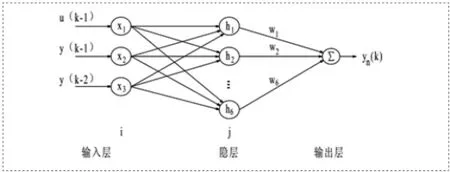
图2 RBF神经网络辨识器拓扑图

其中，X=[x1，x2，x3]T为神经网络的输入向量。u(k-1)为速度控制器输出iq*延时1个周期的采样值，其作为x1节点的输入。y(k-1)为PMSM转速ω延时1个周期的采样值，其作为x2节点的输入。y(k-2) 为PMSM转速ω延时2个周期的采样值，其作为x3节点的输入。通过对PMSM伺服系统的辨识，RBF神经网络输出对PMSM转速的估计值yn(k)。H=[h1，h2，…，h6]T为径向基向量，hj为高斯基函数，即：

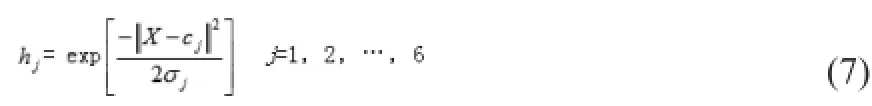
上式中，网络的第j个节点的中心向量为：

基宽向量为：

RBF神经网络的输出为：

RBF神经网络的逼近性能指标函数为：

上式中，y(k)为PMSM的实际转速值ω的采样值。

根据梯度下降法调整RFB神经网络的各参数，可得网络节点中心矢量、节点基宽、输出权值的迭代算法如下：

式中，η为学习率，α为动量因子，η∈[0，1]，α∈[0，1]。

由RBF神经网络辨识得到单输入单输出系统的Jacobian值，算法如下：

该值反应了对象输出对其输入的敏感程度。

3 单神经元PID控制器

若干单神经元依照特定规则可构建成神经网络，神经网络具备自适应和自学习的能力，而单个神经元同样具备这样的能力，且结构简单便于计算。传统PID控制器同样具备结构简单、便于调整和参数整定与工程控制指标联系密切等特点。若将这两者结合，则可以在一定程度上解决传统PID控制器不能实现参数在线整定这一缺点。基于以上这些特点，单神经元PID控制器便于对一些复杂过程和参数时变系统进行有效控制。

3.1 固定K值单神经元PID控制器

单神经元PID速度控制器的模型如图3所示。

图3 单神经元PID速度控制器原理图

图3 中，r(k)为伺服系统的速度给定值，y(k)为PMSM的实际转速测定值，两者作为转换器的输入，经转换器转换为单神经元的输入量x1、x2、x3，K为比例系数，w1、w2、w3为神经元连接权值，使性能指标函数JC减小的趋势来调节神经元连接权值。转换器内部算法如下：

设xi(k)(i=1,2,3)输入的连接权值为wi(k)(i=1,2,3)，神经元的比例系数为K，使用线性截断函数作为变换核函数f(I)，则单神经元PID控制器的输入输出关系可表示为：

控制量u(k)的增量Δu(k)为：

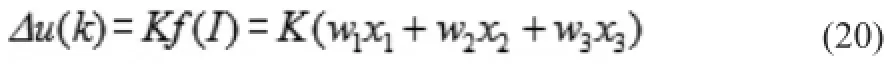
进一步可表示为：

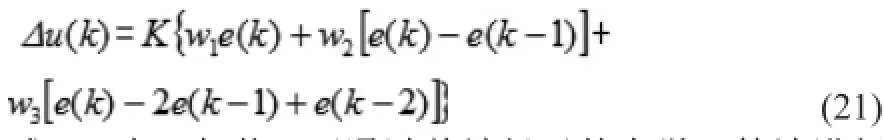
式(21)中，权值wi可通过单神经元的自学习算法进行自整定。正是因为这种特性，单神经元PID控制器对系统数学模型的精确程度要求不高且具有较高的鲁棒性，适用于系统数学模型复杂、外部扰动大、参数时变的被控对象。

本文使用最优控制中二次型性能指标函数的算法思想实现单神经元的自学习，即通过二次型性能指标函数调整单神经元的连接权值，实现对系统输出误差的约束。

单神经元PID控制器的二次型性能指标函数为：

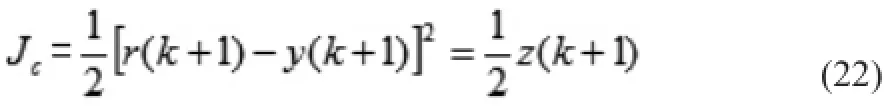
为实现单神经元PID最优控制，沿JC的减小方向修正连接权值wi( k)，即向连接权值的负梯度方向搜索，算法如下式：

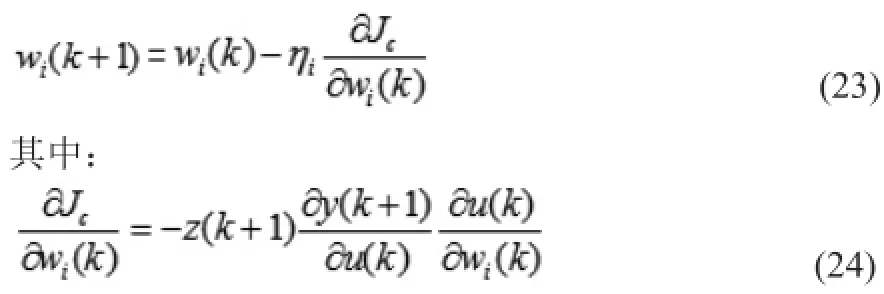
利用式(17)和(20)，并将上式(24)带入式(23)，可得单神经元PID控制器中权系数的调整算法为：

3.2 改进比例系数K的单神经元PID控制器

单神经元PID控制器的比例系数K对控制性能有着较大的影响。K值越大控制器的快速性越好，但将会出现震荡超调。过小的K值虽然可避免震荡超调，但会使系统到达稳态的时间增大。由此可见，固定的比例系数K值存在局限性，不能使控制性能达到最优。

鉴于此，本文对单神经元PID控制器的比例系数K进行改进，令改进后的比例系数为Kc，其值是系统控制误差的函数。

可表示为下式：

上式中，a0、a1为正常数，ωr为PMSM伺服系统的给定速度，e(k)为控制误差。

由式(26)可看出，在PMSM伺服系统达到给定速度值r的初始阶段，可以认为Kc=a0+a1。在PMSM伺服系统进入稳态，即速度达到给定速度值ωr时，Kc=a0。当速度出现超调时Kc= a0－│e(k)│a1/ωr，但此时│e(k)│相对较小，可忽略掉第二项的影响，于是Kc≈a0。易知Kc∈[a0，a0+a1]，PMSM伺服系统速度从0到达给定速度ωr的过程中Kc从a0+a1变化到a0。

此算法与常规单神经元PID算法对比，在PMSM伺服系统速度上升的起始阶段，比例系数Kc较大，保证了系统的快速性，在速度接近稳态时Kc变得较小抑制了速度的超调震荡。

4 系统建模与仿真

4.1 速度控制器建模与算法

用RBF神经网络对PMSM伺服系统进行辨识，其输出将逼近被控系统的实际输出。这样就可得到单神经元PID控制器的对象输入对其输出的Jacobian矩阵，从而实现了单神经元PID控制器参数在线整定。基于RBF神经网络辨识器的单神经元PID控制器原理框图如图4所示。

图4 基于RBF神经网络辨识器的单神经元PID控制器原理图

图4 所示中，神经元PID为单神经元PID控制器。Z－为延时器，其作用是将信号延时一个采样周期。RBF为RBF神经网络辨识器。r(k)为伺服系统的速度给定值，y(k)为PMSM的实际转速测定值，yn(k)为RBF神经网络对PMSM转速的估计值。

对PMSM伺服系统的采样数据进行离线学习获得RBF神经网络辨识器的初始参数。当系统启动后RBF神经网络和单神经元权值将自动调整，且朝着使系统性能指标函数最优的方向变化。具体过程如下：

(1)初始化RBF神经网络辨识器参数,即对神经网络的基宽半径、隐节点中心向量、连接突触权值、学习率、动量因子等参数进行初始化；

(2)对系统的输入r(k)和输出y(k)进行采样，得到系统控制误差e(k)，再由式(17)得到神经元的输入x1、x2、x3；

(3)通过RBF神经网络辨识器估计被控对象的输出值yn(k)，再利用被控对象的输出误差en(k)，根据梯度下降算法调整RBF神经网络辨识器的内部参数，并计算Jacobian值；

(4)利用二次性能指标函数和梯度下降算法再结合RBF神经网络辨识器所得到的Jacobian信息调整单神经元PID控制值的连接突触权值；

(5)计算单神经元PID控制器的输出值u(k)；

(6)令k=k+1返回第2)步，进行下一次迭代。

4.2 系统仿真建模

上文对PMSM矢量控制、单神经元PID控制器和RBF神经网络辨识器进行了详细的论述。接下来对系统进行建模，分别对传统PID控制器、基于RBF神经网络辨识器的固定比例系数单神经元PID控制器和基于RBF神经网络辨识器的改进比例系数单神经元PID控制器进行仿真，比较仿真结果，对提出的理论进行验证。仿真系统框图如图5所示。

图5 系统仿真框图

使用RBF神经网络辨识器的单神经元PID作为PMSM伺服系统的速度控制器，为了便于和传统PID控制器对比，通过选择开关在两者间进行切换。通过编写转换代码，单神经元PID控制器可选择使用固定比例系数或改进比例系数。使用matlab编写RBF神经网络辨识器和单神经元PID控制器的S-function函数，利用simulink搭建PMSM矢量控制模型。仿真模型如图6所示。

图6所示中，PID模块为传统PID控制器，RBF PID为基于RBF神经网络辨识器的单神经元PID控制器，两者通过Switch开关进行切换。编写控制器转换代码，以便对三种不同的控制器的性能进行对比，通过比较可评价三种不同控制器的性能。

仿真模型中PMSM的参数如表1所示。

表1

系统的初始负载转矩设置为4N.m，在0.5s设置负载转矩为9N.m，即模拟外部扰动对系统的影响。系统的速度给定为800rpm。

4.3 系统仿真结果

为了在同一条件下比较不同速度控制器的性能，使基于RBF神经网络辨识器的单神经元PID控制器的初始状态与传统PID控制器相同，做以下处理：

上式中，KP、KI、KD为传统PID控制器的PID参数，K为单神经元的比例系数，w1、w2、w3为单神经元连接权值。

将传统PID控制器、基于RBF神经网络辨识器的固定比例系数单神经元PID控制器和基于RBF神经网络辨识器的改进比例系数单神经元PID控制器的仿真结果绘制于同一二维图中，仿真结果如图7-9所示。

图7 仿真结果(a)

图7 所示中，PID描述的曲线代表传统PID控制器的仿真结果，RBF-K-PID描述的曲线代表基于RBF神经网络辨识器的固定比例系数单神经元PID控制器的仿真结果，RBF-KC-PID描述的曲线代表基于RBF神经网络辨识器的改进比例系数单神经元PID控制器的仿真结果。标识(b)内的曲线反映了三种控制器的动态性能，如图8所示，标识(c)内的曲线反映了三种控制器的抗扰性能，如图9所示。

图8 仿真结果(b)

通过图8所示可得三种速度控制器的动态性能指标，主要动态性能指标参数如表2所示。

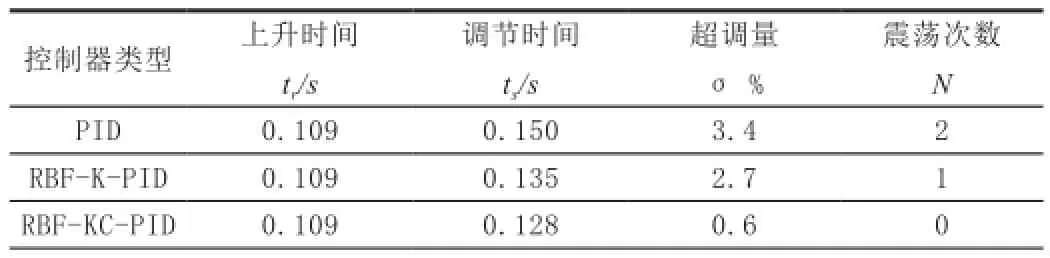
表2 三种速度控制器的动态性能指标

通过对三种速度控制器的对比，可以看出基于RBF神经网络辨识器的单神经元PID控制器的调节时间、超调量、震荡次数等性能指标均优于传统PID控制器，改进比例系数的单神经元PID控制器的动态性能指标优于固定K值单神经元PID控制器，尤其在超调量和震荡次数指标方面较为优越。

图9 仿真结果(c)

通过图9可得三种速度控制器的抗扰性能指标，主要抗扰性能指标参数如表3所示。

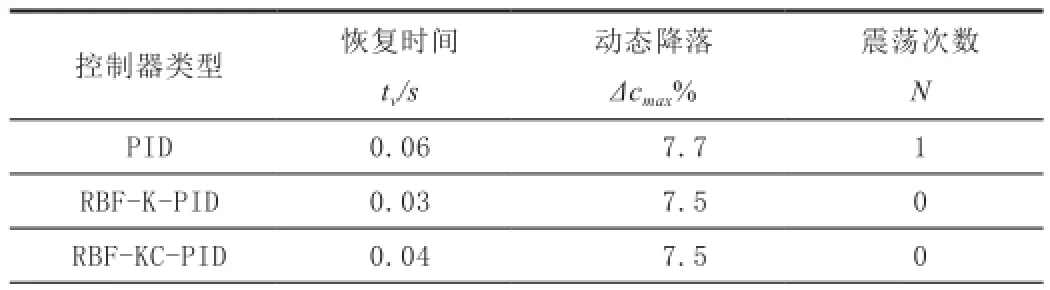
表3 三种速度控制器的抗扰性能指标

通过对三种速度控制器的对比，可以看出基于RBF神经网络辨识器的单神经元PID控制器的恢复时间、动态降落、震荡次数等性能指标均优于传统PID控制器。而改进比例系数的单神经元PID控制器的恢复时间较固定比例系数的单神经元PID控制器长，但其速度曲线几乎无超调和波动现象。由此可见使用优化比例系数的单神经元PID控制器可大大提高系统的控制性能，使系统更加平稳，抗干绕能力更强。改进比例系数的单神经元PID控制器以牺牲系统扰动恢复时间为代价换取了平稳的控制性能，其特别适用于柔性控制。

5 结束语

笔者提出了一种基于RBF神经网络辨识器的单神经元PID控制器，作为PMSM伺服系统的速度控制器。进一步，对固定比例系数的单神经元PID控制器进行优化。

利用matlab的simulink模块搭建PMSM伺服系统模型，并分别对传统PID控制器、基于RBF神经网络辨识器的固定比例系数单神经元PID控制器和基于RBF神经网络辨识器的改进比例系数单神经元PID控制器进行了仿真，通过对三者仿真结果的对比，验证了基于RBF神经网络辨识器的单神经元PID控制器在同样的初始条件下具有比传统PID控制器更加优越的控制性能。

通过对比基于RBF神经网络辨识器的固定比例系数单神经元PID控制器和基于RBF神经网络辨识器的优化比例系数单神经元PID控制器的仿真结果，验证了基于RBF神经网络辨识器的优化比例系数单神经元PID控制器具有更加平稳的控制性能和抗干绕能力，但是其抗扰恢复时间较长。

[1]张静．基于FPGA的温室智能控制方法及关键技术研究[M]．北京:西北农林科技大学,2007．

[2]肖博．交流伺服系统参数整定方法及抗负载扰动观测研究[D]．湖南:湖南大学,2014．

[3]刘可述．PMSM伺服系统速度环和位置环控制器参数自整定技术[D]．哈尔滨:哈尔滨工业大学,2012．

[4]田景文,高美娟．人工神经网络算法研究及其应用[M]．北京:北京理工大学,2006,27:213-264．

[5]Simon Haykin．神经网络原理[M]．北京:机械工业出版社,2004:207-225．

[6]曾喆昭,向印中．一种基于非线性PID神经网络算法的PMSM控制[J]．长沙:电力科学与技术学报,2012,27(4(6):70-75．

[7]Raiani K．Mudi,Chanchal Dey,Tsu-Tian Lee．An Improved Aotu-tuning Scheme for PI Controllers[J]．ISA Transaction,1984,20:645-651．

[8]Misir D,Malki H．A,Chen G．R．Design and Analysis of A Fuzzy Proportional-Integral-Derivative Controller[J]．Fu-zzy Sets and Systems,1998,6(4):449-463．

[9]刘锦波,张承慧．电机与拖动[M]．北京:清华大学出版社,2006:301-351．

A PMSM Speed Controller Based on RBF Neural Network and Single Neuron PID

Song Yongqiang1，Liu Yicong2，Zhu Hongguang3
（1.Manyang Weibo Electronic Co.,Ltd，Mianyang 621000，China；2.Weapon Equipment Information & Control，Mianyang 621000，China；3.Manyang Weibo Electronic Co.,Ltd，Mianyang 621000，China）

In order to improve the control performance of PMSM(Permanent Magnet Synchronous Motor)servo system，the paper proposes a PMSM speed controller based on RBF(Radial Basis Function)neural network and single neuron PID，which realizes self-tuning of the speed controller’s internal parameters in accordance with the real-time status of PMSM servo system.Due to this ability，it makes the system’s speed loop realize the optimal control on the whole.In reality，industrial process control has a higher requirement for smoothness. Therefore，improvement is made to the single neuron PID algorithm by modifying the fxed scale factor into a variable proportional coeffcient changing with system error，which effectively reduces the system overshoot and thereby makes the control smoother.

PMSM；RBF neural network；single neuron PID controller