第十讲镍基合金基带电化学抛光研究
——均匀设计应用解读
2017-02-17徐静安彭东辉李志刚
徐静安 彭东辉 李志刚
技术讲坛
第十讲镍基合金基带电化学抛光研究
——均匀设计应用解读
徐静安 彭东辉 李志刚
案例摘录于《高温超导材料-镍基合金基带表面精饰技术研究》。硕士论文学生朱海,导师吴向阳、彭东辉两位教授级高级工程师,导师助理韩婕,2014年5月9日通过了论文答辩。笔者摘采引用,重点是对均匀设计应用中带有普遍意义的几个问题展开了讨论。
镍基合金基带厚约0.08 mm,要求电化学抛光后,表面粗糙度Rms<10 nm。通过电化学抛光-溶解将冷轧基带表面大小角度晶界及晶界沟槽效应消除,又不能大尺度地减薄基带,技术上必须从工程电化学抛光提升到纳米级的表面精饰处理研究。为此,对不同基带材料抛光液-电解液、抛光工艺筛选,提出了更精准的优化要求。
此外,受到硕士研究生有限的学术研究时间的制约,不可能采用传统的单因素考察来进行大范围筛选。
在导师扎实的电化学专业知识指导下,上海化工研究院支持采购原子力显微镜(AFM)自建测试表征手段,朱海硕士学习、应用均匀设计及数据处理技术,使研究工作取得了阶段性进展。由于朱海硕士已经离开上海化工研究院,笔者和彭东辉教授级高工、李志刚硕士作了进一步讨论、计算、解读。
一、使用均匀设计作探索性试验
在镍基合金基带阳极极化行为的前期研究中,依靠专业知识的技术逻辑,粗选了具有一定可抛光特性的电解抛光液体系。但可使用的正磷酸、浓硫酸、有机添加剂主体系及其抛光工艺尚达不到表面粗糙度Rms<10 nm的精饰要求,尚需在较大配比范围内搜索、筛选。
进一步的细筛抛光液配比,需学习、试用专门的混料设计-配方设计;乃至配方设计耦合工艺组合的均匀设计,需花费一定时间。
为此,探索性地选用了U6(63×2)混合均匀设计表(见参考文档中的表1)。即使按该表的考察因子个数及相应的水平数,全面组合试验的实验次数N1=63×2=432次,实验工作量较大。
参考文档的表1中电解液配比是个三元配方体系,按传统的均匀设计应用,也是在每一个配方条件下,对反应工艺条件安排一次(64)均匀设计。对本案例考察6组配方,实验次数N2=6×6=36次,实验工作量也不小。
电解液三元配比是个定性因子,也就是说难以用一个定量值来表示这个因子的特征。在本案例中,由于研究工作受到一定的制约,故决定探索性地选用参考文档的表1数据,将定性因子作为X1列入均匀表中,实验次数N3=6次。在均匀设计中,定性因子变量水平就不要求单调增或单调减来进行排序。
参考文档的表1实验结果表明,No.3,No.6的Rms<10 nm,探索结果良好。参考文档的表1考察4个因子,由于均匀设计保证了研究对象在四维空间中的均匀布点,即使研究对象在研究范围内是个多峰函数,这些均匀组合的实验点也能以较高的概率,直观地表达峰值区域及“好点”方向。
含定性因子的均匀设计及统计建模有专门的计算方法,本讲座将在以后专门讨论。
本案例采用直观分析,结合专业知识,探索性筛选优化组合,为后续研究工作提供进一步优化基础。用均匀设计作探索实验,快速搜索优化组合,是本案例的亮点。
二、使用均匀设计作优化实验
本案例根据U6(63×2)的实验结果,AFM表征形貌,并结合电化学专业知识直观分析、选择No.3,兼顾No.6进行进一步的精选优化实验,试验方案选用U6(62×3×2)混合均匀表(见参考文档的表2)。
由于基带材料、轧制工艺、电解抛光电压、电解液浓度等的不稳定性,可能影响AFM的测试结果,即激光扫描测定的表面粗糙度Rms在纳米尺度上有一定的离散性。为此,在优化实验时要求每个实验组合重复n≥3。
在使用DPS统计建模时,为求取极大值,对Y进行变换Y=1/Rms。
实验结果的直观分析,在探索细筛试验参考文档的表1中,1/3实验结果Rms<5 nm;在筛选优化试验参考文档的表2中,有13/21实验结果Rms<5 nm、19/21实验结果Rms<10 nm,说明试验设计所选取的因子及考察范围在逐步逼近多维空间中较优的峰值区域。
三、使用均匀设计统计建模的学习修整
根据参考文档的表2实验结果,用DPS软件的二次多项式逐步回归建模,对回归方程逐项检验,可以认为回归方程统计意义上显著,可以接受。这里需要强调的是,这个统计检验结论是针对实验结果、统计模型的拟合功能而言的,统计模型的另一个预报功能尚未得到验证。
统计模型的预报功能,数理统计学家开发了“留一法”,构筑了PRESS、R2(预报)等统计量,进行相应计算,对预测结果进行整体评估。本案例中,对求取的优化工艺组合,采用可靠的工程化法-验证试验。
结合本案例,获得模型1:

预报最优值Rms=3.38 nm及工艺组合,经验证实验为Rms=2.749 nm。尽管预报值及验证实验值Rms<5 nm,均达到了表面精饰的Rms<10 nm的研发目标,但是二者相对误差为22.95%,从数理统计角度来看,模型的预报功能尚需学习、修整。
那么如何进行学习、修整?相关专著、案例无一给出建议和示范讨论。笔者在推广应用中,根据数理统计基本知识给出建议,取得很好成效。
建议一是将探索实验中和参考文档的表2中考察因子相同,各因子值处于均匀设计范围内的组合条件和Y值找出来。具体来说,还可挖掘出参考文档的表1中No.3是符合的,从而用合并后的实验数据进行学习、修整,统计建模。
建议二是直接利用参考文档的表2模型的实验验证值,作为新的No.7,进行建模,得到模型2:
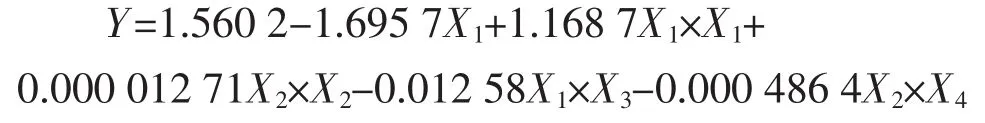
统计模型经各项检验显著,拟合效果可以接受。对于预测值进行验证实验,三次平均值为Rms=3.353 nm,模型预测值与实验验证值相对误差8.14%,且三次验证值均为Rms<5 nm,认为可以接受。模型得到了学习、修整。
那么进一步引伸,以参考文档的表2混合均匀设计表数据为基础,加上探索实验时在此范围内的参考文档的表1中No.3一组,再加上参考文档的表2中模型1的验证性数据,以及模型2的验证性数据进行学习、修整,效果如何呢?计算结果见附件,得到模型3,进行学习、修整的效果评估。在评估表中斜向箭头表示相应指标的微升或微降,横线表示回归方程拟合标准差S变化持平。由于模型3预报优化值的工艺组合和模型1,2预报工艺组合基本一致,并进行相应验证,可不必再行验证,评估表中直接引用。评估结果表明,除S持平外,各项指标均有不同程度的改善,尤其是偏回归系数P下降明显,综合表明进一步学习、修整后,模型3拟合及优化值预报的稳定性得到改善提高。结果见表1。
曾有神学家热心于讨论“针头上能有多少天使在跳舞”的无聊问题。但我们热心于计算、解读、挖掘、讨论的目的是结合具体项目学习、正确应用试验设计及数据处理技术。专业组的研究人员热心于此是为了提高研发效率和水平;而笔者热心于此是与专业研究人员进行探讨,从具体的专业特殊性中抽提出适用的普遍性方法,并从具体的专业个性化研究中提炼出适用的共性技术,与同仁们共享。

表1 评估结果
参考文档:
镍基合金基带的电化学抛光及结果表征
以LPS3030D型直流稳压/稳流电源作为恒流电源,采用恒电流电解抛光方法对镍基合金基带表面进行电化学抛光处理,试验装置见图1。试验过程中以纯镍片作为阴极,镍基合金基带作为阳极。其中,阳极试样尺寸为10×10 mm,阴、阳极面积比为4∶1。以CHI1015型超级恒温水浴槽对抛光温度进行控制。

图1 电化学抛光试验装置图
抛光后的镍基合金基带表面形貌采用BioScope (USA)和MicroNano D5A(China)两种型号的原子力显微镜(AFM)进行表征,随机获取25×25 μm测试范围内二维和三维图谱,最后进行表面粗糙度分析。
Ni-5%W(原子分数)合金基带电化学抛光技术的研究:
(1)Ni-5%W(原子分数)合金基带电化学抛光工艺的初步探索
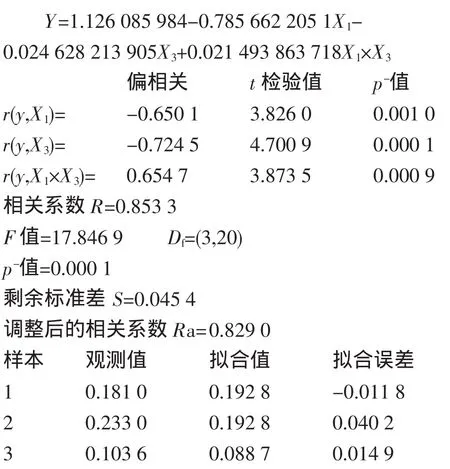
影响电化学抛光结果的主要因素有抛光液的组成、抛光时间、电流密度、温度等。本文以85%正磷酸、98%浓硫酸及有机添加剂组成三元配方体系,在室温25℃条件下,考察电解液中磷酸、硫酸、有机添加剂的配比条件(X1),抛光电流密度(X2),抛光时间(X3)和阴阳极间极间距(X4)四个因素对Ni-5%W(原子分数)合金基带表面均方根粗糙度Rms的影响,其中X1、X2及X3三个因素取6水平,X4一个因素取2水平。Ni-5%W(原子分数)合金基带由德累斯顿evicoGmbH股份有限公司(德国)生产,立方织构比例>98%。试验中,根据因素数和试验水平数,参考U6(63×2)混合水平均匀设计表安排试验,以Ni-5%W(原子分数)合金基带表面在25×25 μm范围内均方根粗糙度Rms来表征结果,具体试验方案及抛光结果见表1。
图2为表1中第3号试验方案实验结果的原子力显微镜(AFM)二维和三维形貌图。由图2可知,经过电化学抛光处理后的基带表面凸起物明显减少或减弱,冷轧过程中产生的沟槽效应已经明显不存在,且大、小角度晶界消失,试验具有较好的效果。
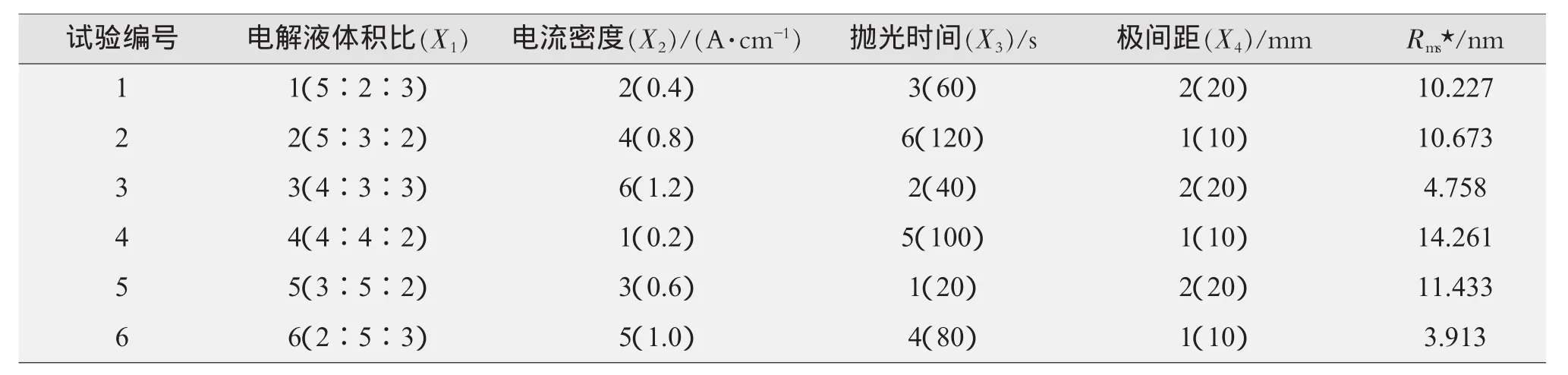
表1 U6(63×2)试验方案及结果
(2)Ni-5%W(原子分数)合金基带的电化学抛光工艺的优化
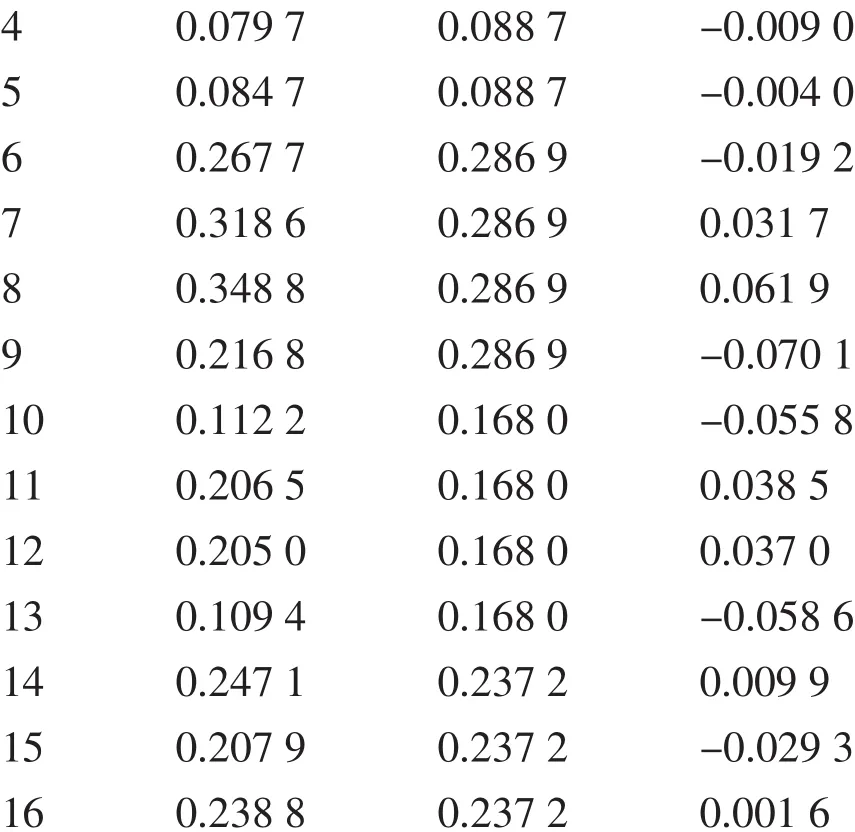
由表1中原子力显微镜(AFM)分析结果可以看出,3号和6号试验结果在25×25 μm测试范围内均方根粗糙度Rms均小于5 nm,都是比较好的方案。为了进一步研究其工艺参数对抛光结果的影响,根据3号试验结果中的原子力显微镜形貌优于6号试验方案的结果,并综合考虑电解液组成等因素,故选取3号方案中的电解液组成配比条件,同时引入变量温度因素,将电流密度取值范围减小,抛光时间、极间距范围保持不变,再次安排试验考查电流密度(X1)、抛光时间(X2)、试验温度(X3)和极间距(X4)四因素对抛光质量的影响。其中,X1和X2两因素取6水平,X3因素取3水平,X4因素取2水平。根据各因素数和水平数,选取U6(62×3×2)混合水平均匀设计表安排试验,以平整度Y(Y=1/Rms)作为考核指标,具体试验方案及测试结果见表2。
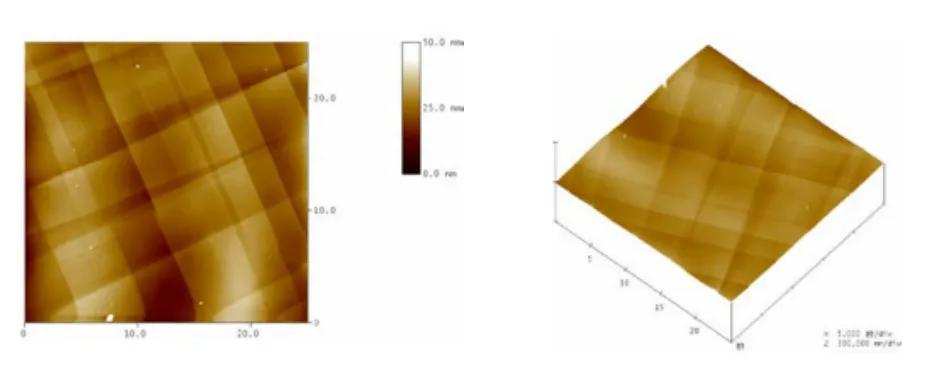
图2 Ni-5%W(原子分数)合金基带在磷酸、硫酸和有机添加剂体积比为4∶3∶3,在25℃,电流密度为1.2 A·cm-2,抛光时间40 s,极间距20 mm条件下抛光后的表面AFM形貌(Rms:4.758 nm)
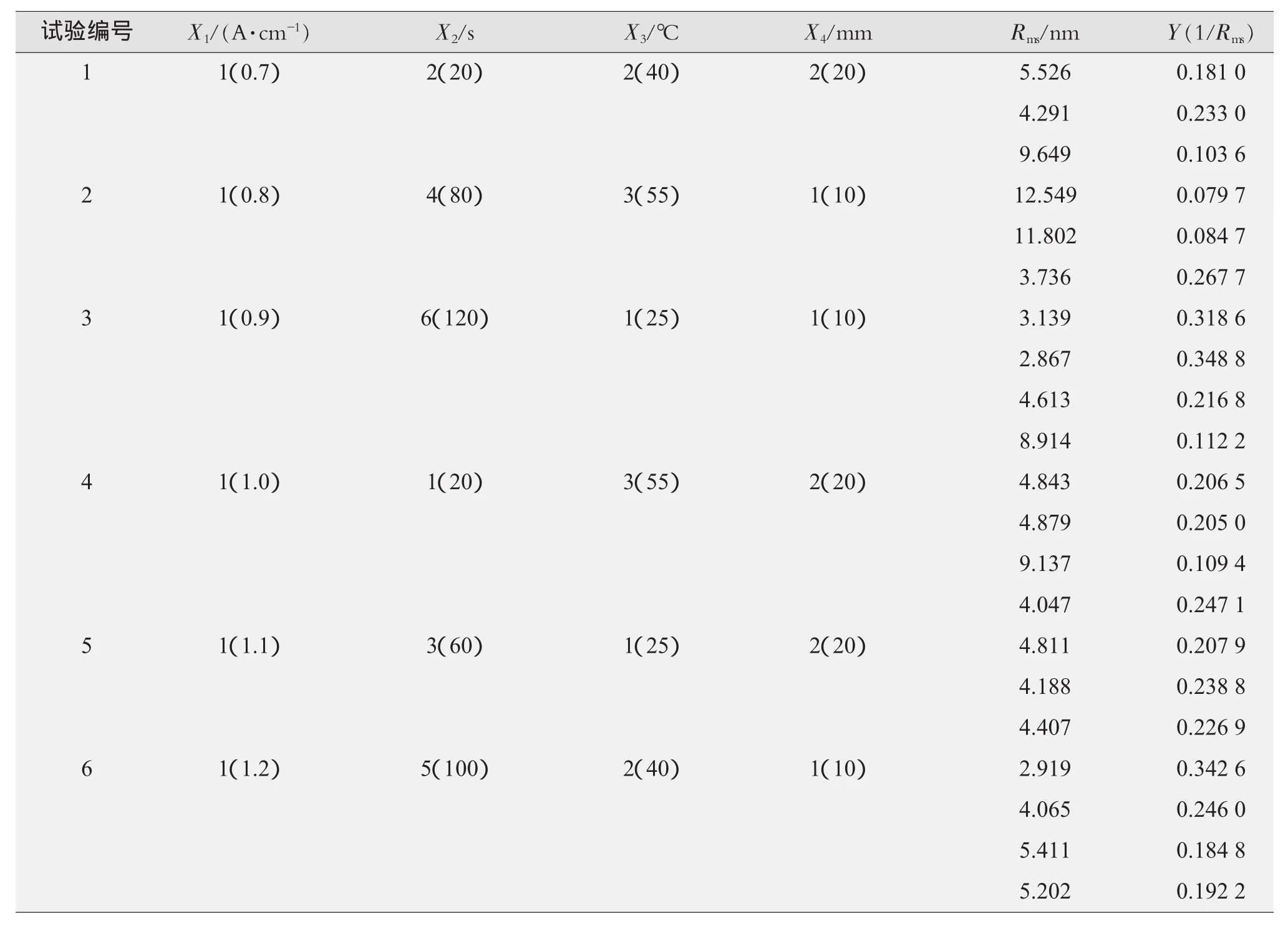
表2 U6(62×3×2)试验方案及结果
采用二次多项式逐步回归分析方法用于试验数据处理,可以分析出影响因变量的各主要因素和各因素之间是否存在交互作用,以及交互作用的强弱,并且可以得出“最优”回归方程的Y=f(Xi)表达式。同时,根据预测的最高指标值进行实验验证,可以对回归模型进行不断优化,从而得到最佳试验结果。本文为满足回归方程最高指标值时拟合条件,以平整度Y作为评价指标,对表2试验方案中的试验结果进行逐步回归分析,拟合后回归方程为:
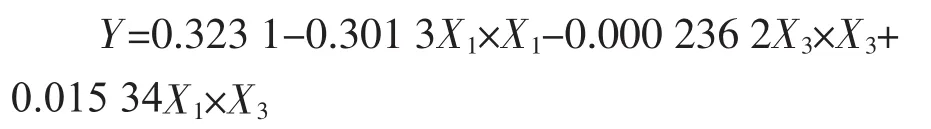
其中,P-值=0.000 2,小于0.05;相关系数R= 0.822 8,调整后的相关系数Ra=0.787 3;Df(3,17),F值=11.873 1,查f分布(α=0.05),F=3.20<11.873 1,相关性显著;最大拟合误差为0.095 6,与剩余标准偏差S=0.048 1的比值为1.988,可以认为该回归方程显著。
通过对回归方程求取最优值,最高指标时各因素组合:
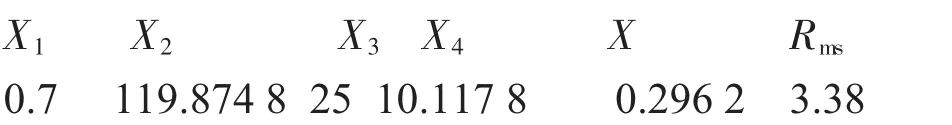
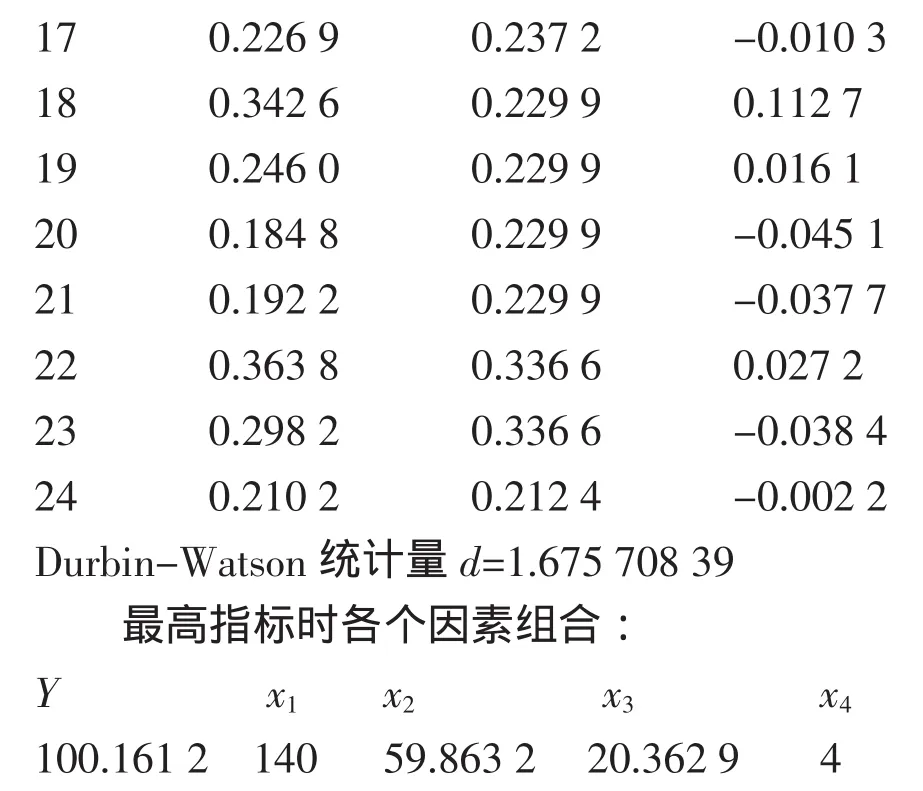
利用上述技术参数在同样试验条件下进行验证实验,得出实验值为2.749 nm,模型预测值与实验测值相对误差为:22.95%。由于模型预测值与实验值相对误差较大,因此,将此实验值及相应技术条件添加到表2中,对22组数据进行再次拟合,得到新的特征方程为:
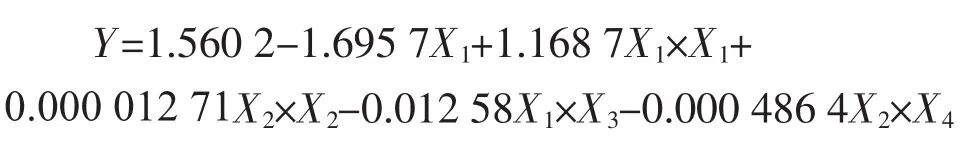
其中,P-值=0.000 5,小于0.05;相关系数R= 0.847 3,调整后的相关系数Ra=0.793 6;Df(5,16),F值=8.145 1,查f分布0.05,F=2.85<8.145 1,相关性显著(*);最大拟合误差为0.097 6,与剩余标准偏差S=0.050 6的比值为1.929,可以认为该回归方程非常显著(**)。
对偏回归系数进行t检验时,由∣t∣大者对应的偏回归系数(见表3)可知,因素主次顺序:X1X3>X2X2>X2X4>X1X1>X1,且交互项X1X3对应的P-值小于0.01,故其对基带表面粗糙度影响高度显著,即在试验范围内,电流密度与抛光温度的交互作用对基带表面粗糙度的影响高度显著。
附件:
参考文档中的表2计算用数据(21组数据放入表1一组(433)及两组验证计算结果):

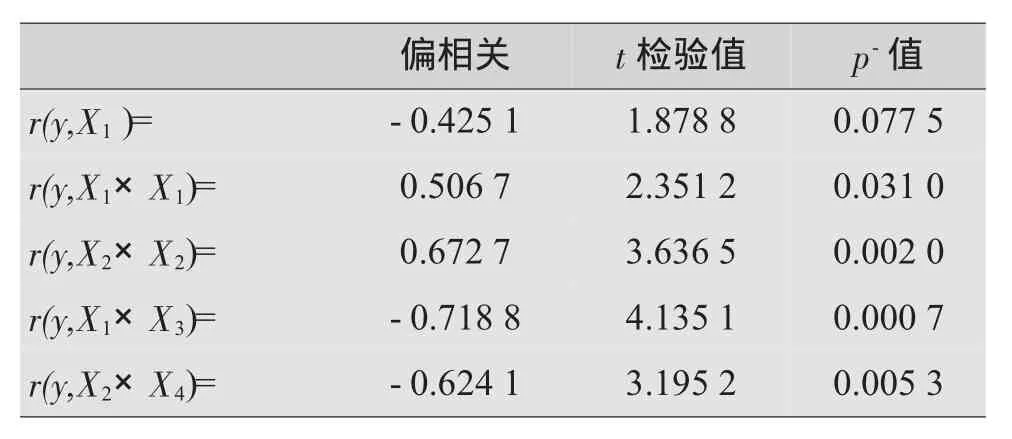
表3 回归系数表
最高指标时各因素组合:

按照上述技术条件对Ni-5%W(原子分数)合金基带进行电解抛光验证实验,利用原子力显微镜(AFM)对基带表面进行表征,结果表明,抛光前基带表面均方根粗糙度Rms为24.280 nm。
对回归方程进行实验证后,得到抛光后的Ni-5%W(原子分数)合金基带表面均方根粗糙度Rms分别为:4.977 nm,2.749 nm,2.333 nm,平均值为3.353 nm,模型预测值与实验验证的平均值相对误差为8.14%,说明回归方程正确、可信。

计算结果见以下数据,得到模型3: