非充分灌溉下精量灌溉决策方法研究

张育斌+魏正英+张磊+张帅+周瑞

摘 要： 针对我国干旱半干旱地区节水灌溉中需要动态调节的问题，提出在灌溉决策中考虑非充分灌溉因素，运用Jensen乘法模型建立“灌水?收益”的数学模型，采用遗传算法、基于SQP算法和基于有效集算法的fmincon函数求解模型，以宝鸡峡灌区冬小麦为例，验证所建模型的准确性及求解方法的可行性，对比计算结果发现，基于SQP算法的fmincon函数运算结果最优，相对遗传算法其灌溉收益提高3%，运行时间降低60%，稳定性优异，并使用该算法进行了非充分优化灌溉下的决策系统设计。

关键词： 非充分灌溉； 序列二次规划算法； 决策； 灌水?收益模型

中图分类号： TN876?34； TP312 文献标识码： A 文章编号： 1004?373X（2017）01?0115?04

Abstract： Since the dynamic adjustment is needed by the water?saving irrigation in arid and semi?arid regions， the ″irrigation?income″ mathematical model established by Jensen multiplication model taking into consideration of the deficit irrigation factor in irrigation decision?making is proposed. The genetic algorithm and fmincon function solving model based on SQP algorithm and active set algorithm are used to verify the accuracy of the established model and the feasibility of the solving method by taking the winter wheat in Baoji gorge irrigation district as the example. The contrast calculation results show that the fmincon function based on SQP algorithm has the optimal operation result， its irrigation income is increased by 3% in comparison with the genetic algorithm， operation time is reduced by 60%， and it has excellent stability. The decision?making system under deficit optimization irrigation was designed with the algorithm.

Keywords： deficit irrigation； SQP algorithm； decision?making； irrigation?income model

0 引 言

1970年美国开始了非充分灌溉的试验，他们后来进行了冬小麦非充分优化灌溉试验，获得了良好的试验效果。80年代澳大利亚的科学家进行了桃树的非充分优化灌溉试验，并且开发出一套亏缺条件下的灌溉方法，不仅节约了灌溉用水，而且还提高了桃树的产量并改善了桃子的品质[1]。

国内学者对非充分优化灌溉的研究虽起步较晚，但研究进展迅速，尤其在我国西北干旱地区。文献[2]使用多维多目标模糊优选动态规划理论求解非充分优化灌溉模型，在非充分灌溉条件下，提高了单位灌溉水的效益。文献[3]采用改进的遗传算法与多维动态规划模型，建立了非充分优化灌溉条件下的灌溉制度，应用于三江平原水稻取得了良好的效果。文献[4]采用PSO及SM?PSO算法求解Jensen模型参数，计算拟合精度较高。

近年来，一些新技术和新算法的出现使得非充分优化灌溉理论及其工程应用的研究呈现出新的发展态势。其中对遗传算法的应用表现的尤为突出，文献[5?7]均使用遗传算法解决非充分灌溉条件下的灌溉模型计算。本文在这些研究的基础上，研究更有效的算法来求解灌溉模型，进一步提高计算精度，为智能决策提供最优方法。

1 灌溉模型建立

2 模型求解

2.1 遗传算法

遗传算法是生物行为的计算机数字化模拟中的重要成果之一，它在历经研究和归纳总结之后发展形成了遗传算法的基础框架[11?12]。其中编码方法、遗传操作、适应度函数设定等技术是遗传算法的基本实现技术。

2.2 fmincon函数

Matlab中提供了求解此问题的函数fmincon[13]，用于求解最优化问题时，可选的算法有四种：内点算法、序列二次规划算法（SQP）、有效集算法（Active set）和基于映射牛顿法的置信域算法，Newton?Lagrange方法中提出序列二次规划（SQP）算法是处理非线性约束优化问题的一种有效方法[14]。有效集方法是基于用等式约束二次规划问题[15]，认为每次迭代均以已知可行点作为起点，并将在该点起作用的约束作为等式约束，而对在该点不起作用的约束暂时不予考虑，这样，就将一般约束的二次规划问题转化为有限个仅带等式约束的二次规划问题。

2.3 灌溉模型求解

分析并采用求解此问题的三种方法，为了验证所建模型的准确性以及求解手段的可行性，应用实测的资料进行求解。实验资料来自于陕西省宝鸡峡灌区某试验田，所测资料为2013年冬小麦六个生育阶段的缺水敏感指数、最大需水值和有效降水值，如表1所示。

下求函数的最大值，在这里以灌溉水平135 mm，灌溉面积为1公顷（10 000 m2）为例，则函数方程转化为：

在约束条件（4）下求解最大值问题。

3 灌溉模型的分析

Matlab中提供的上述三种算法均是求解最小值，因此只需在函数前加上负号转化为求解函数的最小值即可。编写M文件，设置相应的参数，运行结果如表2所示。

由表2预测收益列可以看出，基于SQP算法的fmincon函数预测值最高，其值为9 556元/公顷，大于遗传算法的9 371元/公顷和基于有效集算法的fmincon函数的9 498元/公顷。

同时发现基于SQP算法的fmincon函数预测值不仅最高，而且稳定。这里所说的SQP算法的稳定性是对比遗传算法的不稳定性而言的，借助Matlab平台分别运行这两种算法计算该问题100次，计算出预测收益，将每一次的运行结果统计出来绘制成图，见图1。

从图1中可以清晰地看出基于SQP的fmincon函数的每一次运行结果不变，遗传算法的不稳定性体现的淋漓尽致，导致此现象的原因是遗传算法属于随机类的算法，不能稳定求出最优解。对这100次结果详细分析如表3所示。

在100个数据中最大值为9 521元/公顷（仍小于基于SQP的fmincon函数求得的值），最小值为9 305元/公顷，均值为9 333元/公顷，预测值中9 100～9 300所占比例为21%，预测值中9 300～9 400所占比例为67%，预测值中9 400～9 600所占比例为11%，极差为216元/公顷，标准差为62.8元/公顷。

求解此问题，遗传算法的缺点不仅体现在运行结果的不稳定性上，而且其求解的时间远大于基于SQP的fmincon函数，如图2所示，SQP的fmincon函数运行了9步，而遗传算法运行了50步，运行时间约为SQP的fmincon函数的9倍。

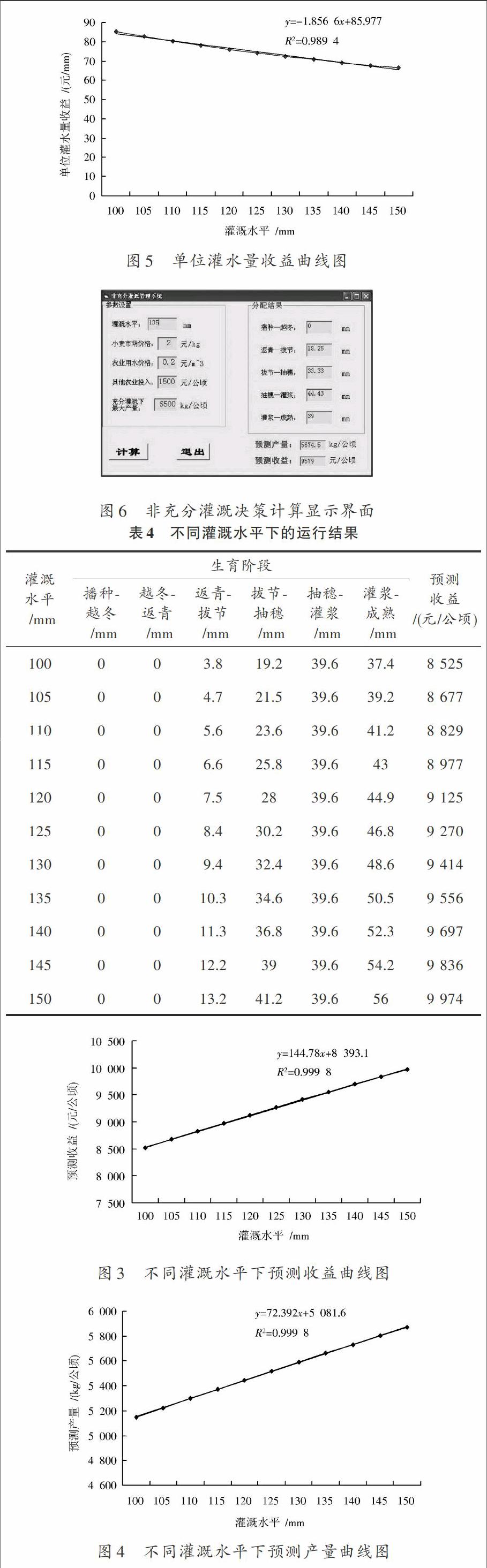
从前面的分析中可以看出，基于SQP的fmincon函数是求解此问题的理想算法，为了全面分析出基于SQP的fmincon函数在不同灌溉水平下的运行结果，分别建立100～150 mm（以5 mm为步长）灌溉水平下的灌溉收益，灌溉产量和单位灌水量收益这三种情况，结果如表4所示，它们之间的关系如图3～图5所示。

从图3～图5可以看出，随着灌溉水平的增加，预测产量和预测收益逐渐增加，单位灌水量收益逐渐减小，而且变化趋势呈线性变化（R2>0.98）。

4 灌溉模型的应用

运用基于SQP的fmincon函数算法进行非充分优化灌溉下决策系统的设计，解决实际问题，需要调用Matlab中的优化工具包，并进行大量参数的设置，十分繁琐。为了便于用户使用，本文进行非充分优化灌溉客户端的设计，具体指使用VB作为客户端，在用户页面中输入灌溉水平，点击计算按钮，后台就可以进行运算并将运行结果显示在用户界面上，实现此功能需要将VB与Matlab混合编程。

启动智能灌溉系统，输入用户名和密码进入主控程序，在非充分灌溉主页面上的灌溉水平一栏内输入灌溉水平，系统将自动运算出冬小麦的每一个生育期的灌溉水平，同时系统将自动运算出预期的产量以及收益，如图6所示。

5 结 论

本文针对我国干旱半干旱地区灌溉决策中考虑非充分灌溉问题，建立了非充分灌溉下“灌水?收益”模型，以遗传算法和fmincon函数为主要方法进行计算与结果分析，并根据峡灌区某实验田的资料进行模型的验证，结果表明，基于SQP算法的fmincon函数方法是该模型的最优求解方法，且运行稳定、运算时间较短。为解决该模型在实际问题的应用价值，采用VB与Matlab混合编程开发了非充分优化下的决策管理系统，为大田智能诊断系统提供了良好的技术平台，推动我国水利工程向智慧化方向发展。

参考文献

[1] 蔡甲冰，刘钰，雷廷武，等.精量灌溉决策定量指标研究现状与进展[J].水科学进展，2004（4）：53l?537.

[2] 陈守煜，马建琴，邱林.多维多目标模糊优选动态规划及其在农业灌溉中的应用[J].水利学报，2002（4）：33?38.

[3] 付强，王立坤，门宝辉，等.推求水稻非充分灌溉下优化灌溉制度的新方法：基于实码加速遗传算法的多维动态规划法[J].水利学报，2003（1）：123?128.

[4] 张志宇，郄志红，侯晓宇.PSO及SM?PSO算法在Jensen模型参数求解中的应用[J].水电能源科学，2013，31（7）：139?142.

[5] 郄志红，韩李明，吴鑫淼.基于改进NSGA?Ⅱ的作物灌水量与灌溉日期同步优化[J].农业机械学报，2011，42（5）：106?110.

[6] 路振广，孟春红，王晓丽.基于遗传算法的冬小麦优化灌溉制度研究[J].人民黃河，2009（11）：76?78.

[7] 郑和祥，史海滨，柴建华，等.基于RAGA?DP的饲草料作物非充分灌溉制度优化模型[J].农业工程学报，2007，23（11）：65?70.

[8] 龚元石.Penman? Monteith 公式与FAO ?PPP?17Penman修正式计算参考作物蒸散量的比较[J].北京农业大学学报，1995，21（1）：68?75.

[9] 刘钰.参照腾发量的新定义及计算方法对比[J].水利学报，1997（6）：27? 33.

[10] 张兵，张建生，黄文生.基于遗传算法的西北旱区灌溉效益决策模型研究[J].节水灌溉，2013（1）：61?65.

[11] POWELL M J D. A fast algorithm for nonlinearly constrained optimization calculations [C]// Proceedings of 1978 the 7th Biennial Conference on Numerical Analysis. Dundee： Springer， 1978： 144?157.

[12] HAN S P. A globally convergent method for nonlinear programming [J]. Journal of optimization theory and applications， 1977， 22（3）： 297?309.

[13] 李明.详解Matlab在最优化计算中的应用[M].北京：电子工业出版社，2011：236?244.

[14] 谢政，李建平.非线性最优化理论与方法[M].北京：高等教育出版社，2010：292?293.

[15] 石国春.关于序列二次规划（SQP）算法求解非线性规划问题的研究[D].兰州：兰州大学，2009.