塑料排水板弯曲通水量对比试验研究

王 婧, 苏林王, 李 涛

(1.中交四航工程研究院有限公司，广州 510230；2.中交交通基础工程环保与安全重点实验室，广州 510230)

塑料排水板弯曲通水量对比试验研究

王 婧1,2, 苏林王1,2, 李 涛1,2

(1.中交四航工程研究院有限公司，广州 510230；2.中交交通基础工程环保与安全重点实验室，广州 510230)

塑料排水板是排水固结加固地基中水分排出的竖向通道。地基处理过程产生的大幅沉降引起排水板弯曲，需要验证其对通水量的对应减小幅值，及对加固效果的影响。通过固定铁框架模型，人为弯曲排水板以简单模拟排水板在工作中的弯曲变形，分析对比4类具有代表性的塑料排水板(常规分离式、防淤堵分离式、常规整体式、防淤堵整体式)在不同弯曲情况下的通水量。研究结果表明：相同的弯曲形式下，常规整体式排水板的通水性能最佳，其次为防淤堵整体式排水板，再次为防淤堵分离式排水板，常规分离式排水板通水量最低；影响塑料排水板通水量的主要因素为排水板芯板、滤膜及弯折形式。

塑料排水板；弯折形式；通水量；对比试验；损失系数

1 研究背景

在真空预压法地基处理中，排水板是其中一个重要的部分。作为地基中水分排出的竖向通道，排水板有助于加快地基的固结，使其能更快达到工程所需的性能[1-3]。地基处理过程产生的大幅沉降引起排水板弯曲，从而导致通水量的减小，进而影响加固效果[4-5]。

塑料排水板在工程应用中随着软土层一起压缩变形，排水板多数情况下并不是在垂直状态下,而是在弯曲状态下进行排水工作的[6-7]。在实验室测定的排水板纵向通水量，只能模拟软土固结初期沉降压缩较小阶段时的排水板通水性能，但是占据整个固结大部分时间弯曲状态的通水性能却并不清晰。为此，本文针对4类具有代表性的塑料排水板，即常规分离式、防淤堵分离式、常规整体式和防淤堵整体式[8-9]，通过固定铁框架模型，手动弯曲排水板以模拟排水板在工作中的弯曲变形，测试4类排水板在不同弯曲情况下的通水量，分析弯曲状态下排水板通水量的影响因素，供实际工程使用参考。

2 试验方案

采用ZEP-I立式通水仪(如图1所示)，排水板上下夹头连同排水板一起，在其外围套上橡胶膜，通过液压系统施加水压力作用于橡胶膜上，其基本原理如图2所示。

图1 ZEP-I型自封式排水板纵向通水仪Fig.1 ZEP-I self-sealing longitudinal drainage meter

图2 排水板通水量测试仪原理示意图Fig.2 Schematic diagram of the principle of drainage capacity meter

试验步骤：

(1) 裁剪好一条48 cm长的排水板(带)样，并套上厚度<0.3 cm,长60 cm的乳胶膜，将两边预留6 cm的乳胶膜与ZEP-I纵向通水仪相连接。

(2) 将ZEP-I纵向通水仪底座降到零位，利用装置上的滑轮将压力室的有机玻璃室上升并固定在通水仪的支撑结构上。在套上乳胶膜的排水板试样两端分别插入通水仪底座下夹头和上夹头，两边预留的乳胶膜分别紧套在通水仪底座下夹头和上夹头外部。

(3) 放下有机玻璃室并与底座固定密封好，打开注水孔并注满压力室，调整接点压力自动补压系统中压力上下限后开始加350 kPa压力。

(4) 在稳定的侧压力和水力梯度下渗流1 h后，每1 h测试1次通水量，直到前后2次通水量差小于前次通水量的5%为止。

为使得试验结果更加准确，试验每0.5 h测定1次，并且校准1次围压，直至读数稳定。

为了能定量地模拟排水板的不同弯折度，通过预制的刚性铁制框架来固定排水板的弯折角度，然后进行相应的通水量试验。不同弯曲形态下的试样长度是按弯折程度放长，通水量的结果也是按长度进行相应修正。具体弯折形式如下：①弯折1次，如图3(b)；②2个方向各弯折1次，共2处，如图3(c)；③一方向弯折1次，另一方向弯折2次，共3处错开，如图3(d)；④竖向倒转，如图3(e)。三弯排水板侧视图和倒折式排水板实物图分别如图4、图5所示。

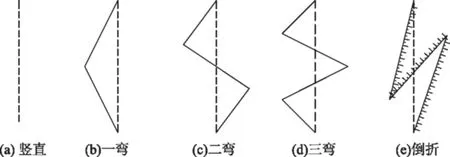
图3 排水板不同弯折形式Fig.3 Bending forms of prefabricated vertical drains(PVDs)

图4 三弯排水板侧视图Fig.4 Sideviewofdrainageboardwiththreebends图5 倒折式排水板实物图Fig.5 Photoofdrainageboardbendedinversely

排水板在水力梯度i=1的条件下，每隔0.5 h进行1次通水，当通水量到达1 000 mL时，记录用时，从而通过式(1)计算排水板的试验通水量。

(1)

式中：qw为排水板通水量(cm3/s)；Q为时间t内的流量(cm3)；l为排水板的有效长度(cm)；Δh为试验水头差(cm)；t为通水历时(s)。

当芯板承受350 kPa的荷载时，竖齿会发生一定变形，使芯板通水面积减小，影响通水量。为考虑排水板在350 kPa围压下可能发生的徐变现象，排水板均须长时间保持围压，当相邻3次通水量读数稳定时，才结束该组的试验。

3 试验结果分析

试验中选取了4种不同类型的排水板，分别为：常规分离式(CF，普通热轧无纺布滤膜，滤膜芯板分离)、常规整体式(CZ，普通热轧无纺布滤膜，滤膜芯板粘合)、防淤堵分离式(FF，新型防淤堵热轧无纺布，滤膜芯板分离)及防淤堵整体式(FZ，新型防淤堵热轧无纺布，滤膜芯板粘合)，排水板芯板的基本性能如表1所示。

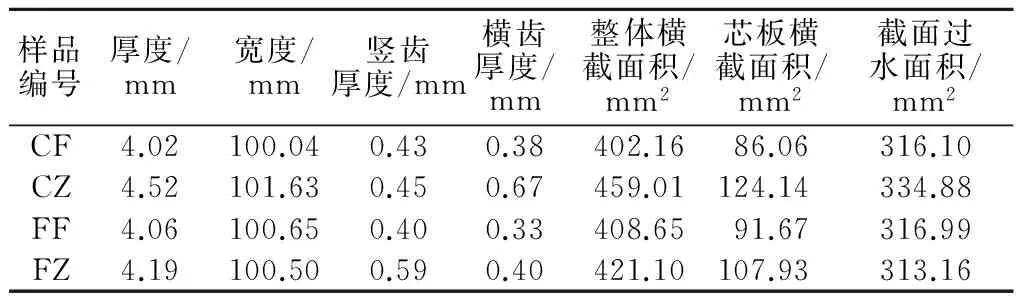
表1 排水板芯板的物理性能Table 1 Physical properties of core veneer of drains

各种弯折形式下4类排水板的通水量-时间曲线如图6所示。

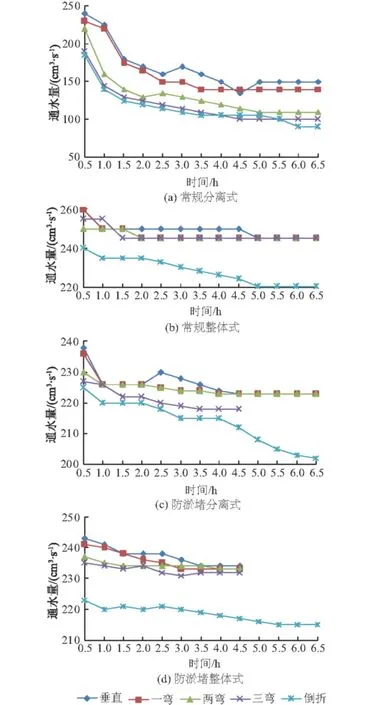
图6 4类排水板弯曲通水量-时间曲线Fig.6 Curves of flow capacity vs. time of PVD in different bending forms

从图6可以看出，这4类排水板的通水量趋势大致相同:随着通水时间的增加，通水量会趋于稳定值；随着弯折次数的增多，通水量均有一定程度的衰减。

从图6还可看出：

(1) 对于常规分离式排水板，在垂直和一弯的情况下，差别并不大，最终通水量只降低了6%，而到两弯形式下，通水量出现了比较明显的衰减，降低了22%；两弯、三弯和倒折情况的通水量差别较小。这意味着排水板存在一个“临界弯折角度”的概念，弯折角度低于临界角，通水性能会发生较大的衰减。常规分离式排水板的临界弯折角度在一弯至二弯之间，试验后也发现，常规分离式排水板在两弯开始，弯折处的竖齿出现明显的倒伏现象，大大影响了通水性能；在两弯、三弯和倒折情况下，弯折处竖齿的倒伏程度并未有所加深。竖齿的倒伏是引起排水板临界弯折角度的原因。

(2) 对于防淤堵分离式排水板，倒折的通水量在试验前4 h内与其余4种弯曲情况接近，在4 h后通水量有了明显下降，主要考虑为在弯折处倒伏的蠕变所致，对排水面积改变的程度越来越大，通水性能出现明显降低。

(3) 对于整体式系列排水板，由垂直状态至三弯状态，通水量衰减程度都很小，衰减最大的也只是降低了1.4%，可以基本考虑为测读误差所致；而在倒折的情况下，通水量衰减相对较大，相对于三弯情况，常规整体式减降10%，防淤堵整体式减降7%。其降低因素主要考虑为在倒折形式下排水板的两侧边出现脱胶现象所致，即最外侧竖齿与滤膜完全脱离，引起单条排水通道的失效。对于这2种排水板，其临界弯折角在三弯与倒折情况之间。

综上所述，在相同的弯曲形式下，常规整体式排水板的通水性能最佳，即使是在倒折状态，其通水量也比常规分离式和防淤堵分离式垂直状态下的要大；其次为防淤堵整体式排水板，从一弯至三弯通水量基本不变，弯曲通水量稳定性能好；再次为防淤堵分离式排水板，通水量降低最大也是发生在倒折状态，降低了7%；通水量最低的为常规分离式排水板，在二弯状态其通水量就有比较大的衰减，从二弯开始到倒折，通水量衰减程度低。

4 通水量影响因素分析

造成弯曲通水量降低的原因有许多方面，主要因素总结如下。

4.1 排水板芯板

该因素主要考虑排水面积和排水面积均匀性这两者引起通水量变化。首先考虑排水面积的影响，芯板在围压350 kPa下有一定的压缩变形，影响排水面积。结合芯板压屈试验350 kPa压力下的应变数据，将排水板排水面积重新计算，得到修正后的排水面积，如表2所示。由表2可见，经过侧压力修正过后，4类排水板的排水面积都很接近。

表2 排水板修正后的排水面积Table 2 Adjusted drainage areas of drainage boards

考虑排水面积均匀性的影响，前述测定排水板截面尺寸时，除常规分离式外，其余三者10个测点的标准差相差很小，但常规分离式的排水通道壁面凹凸不平，均匀性较差，而且壁面有明显的粗糙感。从流体力学的角度来看，壁面粗糙度较高，影响排水速度，其余三者排水通道侧壁光滑平顺，不对流速造成太大的影响。

4.2 滤 膜

滤膜因素主要体现在以下2方面：

(1) 针对分离式系列排水板，其滤膜总周长大于芯板周长，滤膜有更多的“余料”陷入排水通道中，影响排水面积。但这一因素受生产要素的影响，难以定量衡量。

(2) 滤膜受到围压力作用下，横向拉伸变形，陷入排水通道中，影响排水面积，滤膜伸长率越小，则对排水面积的影响就越小。4类排水板均有这方面的影响。为简化计算，取一条排水通道，将排水通道外滤膜受的均布荷载q转化为受集中力F作用，假设滤膜材料处于线弹性变形阶段，模量为E，纵向长度取l，通道宽度为b，滤膜厚度为δ，滤膜与水平夹角为θ。

滤膜受力之后的变形为

(2)

式中：σ为滤膜所受应力；T为滤膜受力。

滤膜中心点根据受力平衡条件,即

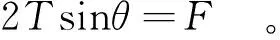
(3)

联立式(2)、式(3)，将防淤堵分离式排水板的截面尺寸代入，即可解得θ=14.464°，此时滤膜应变ε=0.032，仍处于线性阶段，前述假设成立。

排水面积减少量为

(4)

由表2可知，防淤堵分离式排水通道的面积为：

(5)

(6)

可以发现，由滤膜受力横向变形对排水面积的影响为11.8%，同理计算得到常规分离式滤膜受力变形的影响为16.4%。常规分离式滤膜在试验中对排水面积的影响要比新型防淤堵的滤膜材料要大一些，这一点也可以从防淤堵滤膜的定应变负荷值大于常规滤膜可以看出，在相同拉力下，防淤堵滤膜的伸长率要小于常规滤膜，因此对排水面积的影响程度则相对较小。

4.3 弯折形式

4类排水板在不同弯折形式下的通水量如图7所示。

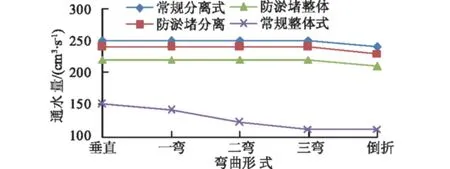
图7 排水板弯曲通水量汇总结果Fig.7 Drainage flow capacities of PVDs in different bending forms

随着排水板弯折次数的增多，不仅仅是排水板的试验长度增加了，流体运动改变的角度也增加了，前者导致沿程损失的增加，后者增大了局部损失。

流体力学中沿程阻力损失的计算式为

(7)

式中：v为排水板内流体速度；g为重力加速度；d为排水板的当量直径。

由式(7)可知，其他条件不变的情况下，排水板试验长度L提高，沿程损失hf线性提高；在排水板弯曲处，会发生流动分离，离心力和压强梯度的断面分布不均匀，在弯曲发生作用下弯头内发展成为双螺旋流(次生流)，再加上弯折处倒伏引起的排水面积的改变，成为局部损失的主要来源。流体运动改变的角度越大，局部损失系数也越大。

下面将分别从局部损失系数理论计算公式和伯努利能量方程这2个方面考虑，定量分析弯折角度与局部损失系数之间的关系。

从局部损失系数理论计算公式出发。根据《水力计算手册》中弯管局部损失系数理论计算式测定4种弯折状态下的弯曲角度，局部损失系数的计算式为

(8)

式中R为水力半径。

以三弯状态为例，弯曲排水板的侧边自上而下每隔3 cm作为一个测点，测量每个测点的坐标，之后将其导入CAD绘图软件进行角度θ测量，半径R采用曲率公式的倒数进行计算。这样θ，d和R已知，可直接套用公式计算ζ。

对于多个弯折次数，其弯折的位置相距过近会有互相干扰的影响，局部损失总效果不等于正常条件下各个ζ值之和。若2个弯折的距离大于3倍直径，互相干扰的影响可忽略不计[7]，且忽略互相干扰的影响使得局部损失计算值偏大，结果也是偏于安全的。

从流体力学的伯努利能量方程出发，伯努利方程为

(9)

式中：H为水头；hj为局部损失。

伯努利方程的使用条件为层流，层流通过雷诺数Re<2 000来判定。取通水量最大的常规整体式排水板，计算其垂直状态下的雷诺数。

雷诺数计算公式为

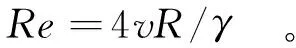
(10)

其中：

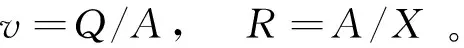
(11)

式中：γ为水的动力黏滞系数;X为排水板的湿周。将常规整体式排水板的各项参数代入式(10)，得到Re=1 157<2 000，故排水板内部流体运动为层流，可以采用伯努利方程。

通水量试验中20 cm的水头差全部转化为动能、沿程损失和局部损失，沿程损失计算公式为

(12)

由此反算出局部损失为

(13)

最终解得局部损失系数ζ。由理论计算公式计算的ζ值和实测反算的ζ值见表3。

表3 不同类型排水板2种计算方式的ζ值Table 3 Values of ζ of PVDs of different bending forms obtained from two calculation methods

注：差值表示各个弯曲形式下ζ的试验反算值减去垂直形式下的ζ值。

由表3可知：

(1) 从弯曲角度可以看到，随着弯折次数的增多，弯折处的夹角越来越小，从垂直的180°减小至倒折形式的44°，夹角越小，意味着排水通道改变的角度也就越大，弯折处产生的局部损失也越大。

(2) 由理论计算值可以发现，4类排水板在不同的弯曲形式下，理论计算ζ值都很接近。计算公式中ζ值只与R，d和弯折角度θ(即夹角)有关，4类排水板修正后的排水面积比较接近，则其当量直径d也大致相等；同一弯曲形式下，θ与R也是相同的，因此4类排水板的理论值很接近。随着弯曲角度的减小，理论局部损失系数越来越大，在一弯的时候只有0.08，局部损失很小；在倒折情况下最大，4类排水板中最大的是常规分离式排水板的12.64。

(3) 从通水量试验的反算ζ值可以看到，在垂直情况下试验反算ζ值都在10以上，主要考虑由试验仪器的误差所致。从通水仪示意图可以看到，从水箱到排水板试样底部有沿程损失，从排水板顶部出来到排水口，也有一段沿程损失，再加上进出排水板的时候，由圆管转变为60个小的矩形排水通道，前后截面变化相当大，在这2个地方的局部损失系数也很大，因此通过试验反算得到的ζ值，在垂直形式下都在10以上。垂直状态下的局部损失，更应该认为是排水板试样段外部的系统损失，因此，各个弯曲形式下的局部损失系数减去垂直形式下的ζ值所得的差值才是排水板内部由弯曲产生的局部损失系数叠加值。

从试验反算值来看，ζ值的变化趋势与理论计算值是一致的，但两者绝对误差较大。一弯形式下ζ值都能达到1以上，常规分离式的ζ差值达到4以上；从一弯到二弯，系数增长较大，除常规分离式的ζ差值增长20倍外，其余三者均增长了4～5倍；从二弯到三弯，增长范围为40%～73.2%；从三弯到倒折，ζ差值增长17%～41%不等，常规分离式增长程度小，其余三者稍大。其变化趋势符合一般规律。

理论值与实测反算值的误差来源于以下2个方面：①理论计算中，将排水面积等效为一个圆管面积，而实际上是由排水板内60条小的排水通道共同工作，流体运动特征与圆管内流动特征并不一致。②理论计算中并未考虑在弯折形式下竖齿的倒伏现象，理论中默认假定了排水面积在不同的弯折形式下是不变的，而实际上排水板在弯折处竖齿很容易倒伏，导致通水面积改变，这一点对于较“软”的芯板来说更容易发生，如图8(a)所示；甚至对于整体式系列的排水板来说，倒折情况下由于竖齿的倒伏变形过大，竖齿与滤膜的胶结会被撕开，造成单条排水通道的失效，如图8(b)所示。

图8 排水板弯折处竖齿的倒伏和脱胶现象Fig.8 Lodging and debonding of vertical teeth at the bend of drainage board

一般来说，局部损失系数可以反映出竖齿倒伏的程度及抗弯性能强弱。以常规分离式和常规整体式排水板为例，在弯曲强度试验中分离式的抗弯强度最低，ζ值在各个阶段都是最大的;在通水试验中分离式竖齿倒伏的情况最严重，在弯折处每一条竖齿都发生波浪状的倒伏。另外在一弯至二弯的过程中ζ差值增大了20倍，而之后增长较小，这就说明常规分离式排水板在二弯的时候竖齿有较大的倒伏变形，之后的弯折形式下倒伏情况加剧不明显，与前述“临界弯折角度”一致。反观整体式排水板，其抗弯强度较大，ζ值较小，试验后的试样除了倒折情况下单边出现脱胶现象外，内部芯板基本无倒伏变形，很好地保持了排水通道的完整性。

在实际应用中应考虑排水板的弯曲导致通水面积变化，而公式法中忽略了倒伏和脱胶现象，导致局部损失系数远小于实际值，不提倡使用公式法进行ζ值的计算，建议通过弯曲通水量试验，反算ζ值。

综上所述，主要考虑影响塑料排水板通水量的如下因素。①排水板芯板:在芯板材质相同的情况下，影响程度与芯板截面尺寸的大小和均匀性相关。②滤膜:整体式滤膜对通水性能的影响程度要小于分离式的滤膜，滤膜的延伸率低，对通水性能的影响也较低。③弯折形式：弯折角度越来越低，通水性能的折减程度也越来越大，弯折角度低于排水板的临界弯折角度，通水量会发生明显的折减。室内排水板弯曲通水量的大小受这3个因素共同作用，互相影响。

5 结 论

本文针对4类具有代表性的塑料排水板，通过固定铁框架模型，手动弯曲排水板以模拟排水板在工作中的弯曲变形，对比分析排水板在不同弯曲情况下的通水量，总结其影响因素，得出以下结论：

(1) 排水板芯板的压曲刚度越大，在土压力和真空负压作用下，芯板变形对通水面积的影响越小，常规整体式排水板排水面积最大，但其压曲刚度较低，由此在围压力作用下与其余三者的排水面积接近，芯板尺寸的均匀性也是影响通水性能的一个要素。

(2) 滤膜在相同拉力下的伸长率越大，对通水能力的影响越显著，同时针对分离式系列的排水板，滤膜有更多的余料陷入排水通道中，对通水能力的影响要大于整体式系列的排水板。

(3) 随着弯折次数的增多，不仅仅是排水板的试验长度增加了，流体运动改变的角度也增加了，前者提高了沿程损失，后者提高了局部损失。

(4) 4类排水板的通水性能大小排序为：常规整体式>防淤堵整体式>防淤堵分离式>常规分离式。

[1] 朱森林. 堆载预压技术在潮汕机场大面积深厚软土地基处理中的应用[J]. 长江科学院院报，2014,31(9): 43-46.

[2] 宣伟丽. 钱塘江涌潮河段防洪堤工程地基处理[J]. 长江科学院院报，2003, 20(4): 58-61.

[3] 宗 明, 邹荣华, 孟 诚. 深圳国际会议展览中心原址软基处理[J]. 长江科学院院报，2002,19(2): 62-64.

[4] WANG Jing, MO Hai-hong, LIU Shu-shuo，etal. Effect of Mineral Composition on Macroscopic and Microscopic Consolidation Properties of Soft Soil [J]. Soil Mechanics and Foundation Engineering,2014, 50(6): 232-237.

[5] 于庆雯，童建国.塑料排水板加固软土地基中涂抹与井阻效应的数值研究[J].电力勘测设计, 2013，(3):24-27.

[6] 应 舒，陈平山. 真空预压法中塑料排水板弯曲对固结的影响[J]. 岩石力学与工程学报，2011，30(增2): 3633-3640.

[7] 高长胜，汪肇京，魏汝龙，等. 固结排水中排水带通水量的影响及选择[J]. 岩土力学， 2004, 25(3): 473-476.

[8] 王 婧，李 涛. 塑料排水板芯板及滤膜物理力学性能研究[J]. 岩土工程学报,2016, 38(增1): 125-129.

[9] 杨 涛，艾长发，张晓靖，等.塑料排水板与碎石桩处理软土地基作用效果对比分析[J].公路，2013，(5):89-93.

(编辑：黄 玲)

Comparative Study on Flow Capacity of Prefabricated Vertical Drainsin Different Bending Forms

WANG Jing1, 2, SU Lin-wang1, 2, LI Tao1, 2

(1.CCCC Fourth Harbor Engineering Institute Co. Ltd., Guangzhou 510230, China;2.CCCC Key Lab of Environmental Protection & Safety in Foundation Engineering of Transportation, Guangzhou 510230, China)

Prefabricated Vertical Drain (PVD) is a vertical channel of water discharge in foundation treated by drainage and consolidation. As the large settlement caused by foundation treatment results in the deflection of PVD, the corresponding decrease of flow capacity and reinforcement effect caused by the deflection of PVD should bestudied. By building fixed iron frame model, PVDs were bended artificially to simulate the bending deformation in real working condition. On this basis, the water discharge capacities of four representative PVDs (conventional type with separated filtration fabrics, anti-silting type with separated filtration fabrics, conventional type with integral filtration fabrics, and anti-silting type with integral filtration fabrics) in different bending conditions were compared. Results indicate that conventional integral drainage board has the best drainage performance in the same bending form, followed by that of anti-silting integral type, filter-separated anti-silting type, and filter-separated conventional type. Core veneer, filtration fabric and bending angle are main factors influencing the flow capacity of PVD.

prefabricated vertical drain; bending form; flow capacity; comparative test; loss coefficient

2016-06-01;

2016-08-08

王 婧(1986-)，女，江西景德镇人，高级工程师，博士，主要从事岩土工程和地下结构方面的研究，(电话)15920333769(电子信箱)phdwangjing@163.com。

10.11988/ckyyb.20161098

TU411

A

1001-5485(2017)02-0017-06

2017,34(2):17-22,40