K-对称-N算法的社交网络的隐私保护

◆高 洁 肖基毅 向 霞

（南华大学计算机科学与技术学院 湖南 421001）

K-对称-N算法的社交网络的隐私保护

◆高 洁 肖基毅 向 霞

（南华大学计算机科学与技术学院 湖南 421001）

针对k匿名算法在对抗结构攻击的不足，采用k-对称匿名算法对社会网络的隐私进行保护。本文对k-对称匿名算法进行可行性分析，并对其还原算法进行描述。虽然社会网络的隐私保护取得了大量的研究成果，社区结构的隐私保护也取得了很多成功，但是其成果都是彼此相对独立的，鲜有将二者兼顾。本文设计出一种k-对称-N匿名算法来解决此类问题。

k-对称匿名; 社区结构; 隐私保护

0 前言

随着社交网络的普及以及数据挖掘的技术的成熟，人们的隐私保护问题成为了近些年来的研究热点。人们在期望信息共享的同时又畏惧着信息共享[1]。太多的信息泄漏事件使得人们不敢将信息放在社交网络上进行交流，这就给数据挖掘等相关科研或者企业带来了一定的困难。一般的社区网络数据发布要在发布之前对数据进行一定的处理才把数据发布到网络中。一般采用泛化与隐匿技术来进行数据的预处理。一般采用简单匿名的方式，但是简单匿名采用自底往上的匿名方式，会使得匿名后的数据可能世界空间加大，无法保持数据的可用性。本文采用不确定性泛化策略来克服这种困难。隐私保护技术现阶段有很多模型被广泛应用。其中为k-匿名模型、l-多样性算法、以及个性化（a，k）-匿名三种最为广泛应用[3]。其中k匿名算法的应用最非常广泛，但是其存在多种不足[4]，本文在其基础上，针对其针对社会网络图中的不足之处提出的改进k-对称匿名算法运用到社区网络之中。社区网络是社交网络中一个经典的问题。社区网络的发现算法包括KL算法、分割算法、谱分割算法、多级别图图分割算法、基于马尔科夫聚类的算法、局部图聚类算法等。本文基于分割算法对社交网络进行社区划分。然后结合k-对称匿名算法提出了k-对称N匿名算法。

1 k-对称-社区匿名算法的实现过程

k-对称-社区匿名算法（K-symmetry-community anonymity algorithm）是一种在基于社区网络划分的前提下的关于结构图的k匿名算法。其流程图如图1下面将对算法进行详情介绍。

2 数据的预处理

传统的社区扰乱技术通常在于扰乱社区内朋友之间的边得关系，并不注重社区结构的保持。我们采用一种特殊的社区扰乱技术。在进行社区划分之前对数据进行简单处理。

（1）迭代查询节点H的社会网络图。H1（节点）、H2（节点的度）、H3（节点的邻接节点的度集合）。

（2）If Hx3==Hy3交换节点Hx、Hy

它使得攻击者事先插入的节点改变了位置，导致攻击错误的攻击到其不感兴趣的社区导致攻击失败。

3 社区划分算法

社区发现技术是本算法研究中核心部分。本算法采用边分割算法，其依据是社区间边的权值betweenness大于社区内边的权值。通过删除较大权值的边来进行社区分割。循环分割直到社区数目达到预期的数目为止。

4 社区聚类

数据挖掘中聚类一般分为三种:基于划分的方法、基于层次的方法、基于密度的方法三种。

本文采用第三种基于密度的聚类方式对社区进行聚类。DBSCAN（Density-Based Spatial Clustering of Applications with Noise）是一个比较有代表性的基于密度的聚类算法。能够把具有足够高密度的区域划分为簇，并能发现任意形状的聚类。

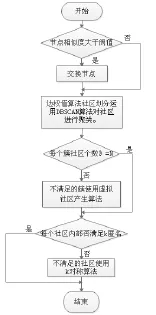
图1 k-对称-N社区隐私保护算法流程图

社区聚类的目地是将相似度大于一定阀值的社区进行聚集，使得一个簇内含有N个社区。这与k匿名算法的思想相同，将每个社区隐藏在与其相似的其余N-1个社区中。并用NMI对社区划分准确度进行测量。

5 虚拟社区的产生

对于一个簇内不满N个的社区采取虚拟社区产生的方式，使其满足一个簇内至少有N个社区。

传统的算法虚拟社区的产生与边的数目都是随机的，这种形式下的虚拟社区与本来存在的社区的差别很大。为了更好的使得社区的产生更加真实化，本文对每个簇内节点期望值与边的期望值作为最初的虚拟社区的节点数目与边的条数，并在簇内随机挑选本簇内的节点作为虚拟社区的节点，并随机生成期望值条边。形成初始的社区。根据公式（1）求此簇内与其他社区内相似度最大的社区。并计算虚拟社区与此社区之间的相似度。

设A1=(M1,N1),A2=(M2,N2)是社区网络A=(M.N)的非空社区。Ni1=Ni(两个社区中的边),Ni2={nxy=(mx,my)∈N|mx∈M1,my∈M2},(两个社区连接边)，Ni3={nx,y=(mx,my) ∈N|mx∈Mi,my∈M-N1-M2}(社区空间中非这两个社区与两社区的连接边)，其中1,2,j=1,2,3,设集合Q，则A1和A2的相似度S(A1,A2)定义为：

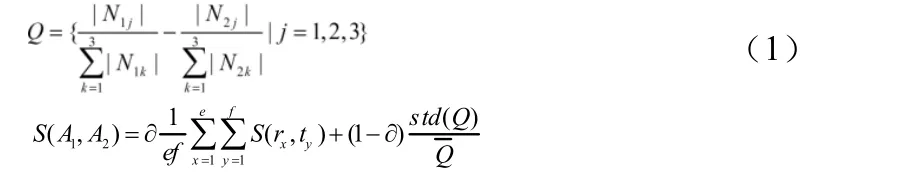
其中∂为加权印子 (0≤∂≤1),其中 ∂用于确定节点相似度(边相似度)占社区相似度所占的比重。std(Q)和分别为实数集合Q中的均值和标准差。e-|M1|,f=|M2|,rx∈M1,ty∈M2。

这种方法即考虑了节点的相似度，也考虑了边的相似度。

若虚拟社区与相似度最大社区之间的相似度小于阀值时，求虚拟社区对相似度最大社区的等异度子集，并将其按度的降序排列的同时将相似度最大的社区度按降序排列，然后将虚拟社区等异度子集度的一半数目的节点用最大社区降序前相同数目的节点替换。将虚拟社区交换后的节点相连的边删除。并在社区内随机产生相同数目的边（边的数目不变原则）。重新计算虚拟社区与相似度最大社区的相似度，小于阀值继续上述步骤。大于阀值则结束。

6 社区内部优化k-对称算法

由于社区的聚类使得每个节点至少隐藏在N个社区之内，但是对于这种隐藏方式与k匿名一样对预防链接攻击有很好的疗效。但一个簇内的社区很大程度上是敏感同质的，对于社区内的节点有时保护度不够，我们对于社区内部再次使用k-对称匿名算法。是其应对对于社区内部的结构攻击。

K-对称匿名算法是k匿名的算法在图论中应用的一种变种。其将图论中的图对称理论运用到k-匿名算法中。简单讲是对社区的节点进行对称处理后再进行k-匿名。本文由于篇幅问题纸描述一个社区的k-对称匿名过程。

其步骤如下:

对图中的节点做出社会网路关系矩阵，本文中因为是无向图，矩阵是对称矩阵。

找出图中自首等价数目最少的节点，对其进行对称处理。判断每个节点是否至少有k个自守等价的节点，不满足重复步骤2。满足则结束。

其是k-匿名算法在图结构的变种，是可行的。相对于传统的将每个节点都做对称处理节点和边都减少很多。复杂度降低。

其还原算法，将最后相同的等价类只留一个，这种还原方法虽然无法百分之百还原原始数据，但在一定程度上还是可取的。

7 实验及分析

将k-对称N社区发现算法在不同的k值下的信息损失与经典的p-Sensitive k-匿名算法进行比较。已判断其数据的真实性。

K-对称-N匿名算法与经典p-Sensitive k-匿名算法信息损失对比如图2。

由实验可知k-对称-N算法比p-Sensitive k-匿名算法数据损失小，证明了其有效性。

其数据隐私保护度相对与传统的k匿名算法又增加了N社区匿名。大大提高了隐私的保护度。