多元线性回归在大坝变形监测数据处理中的应用

李 瑞，姜新元，秦 涛

（四川省水利水电勘测设计研究院测绘分院，四川 成都 610500）

多元线性回归在大坝变形监测数据处理中的应用

李 瑞，姜新元，秦 涛

（四川省水利水电勘测设计研究院测绘分院，四川 成都 610500）

变形监测是保护国家和人民生命财产、减少未来经济损失的重要手段。监测数据分析是变形监测的一个重要环节，它是预测变形体未来发展趋势、验证设计的各项参数的重要依据。结合四川省嘉陵江某水电站变形监测项目，提出多元线性回归在大坝变形监测数据分析中的适用性，阐述了多元线性回归的优缺点，并探讨了该数据模型在工程实例中的运用方法。

多元线性回归；桐子壕水电站；大坝变形监测；垂直位移；水平位移

0 引言

大坝变形监测的目的是掌握闸坝及电厂运行期的工作状态，验证其设计参数，以便及时发现异常情况，并采取措施，从而保证闸坝、电厂的安全运行［1］。通常，监测设施采集到的样本数据不能直接反映大坝的安全性态，需要对观测样本进行分析处理［2］，建立用以反映监测效应量变化规律的监测模型来评价大坝的运行状况。因此，大坝监测资料分析是大坝安全分析的主要环节。

回归分析是对数据变化趋势的分析，也称为曲线回归、趋势外推或趋势曲线分析。它是迄今为止研究最多，也最为流行的定量预测方法。多元线性回归分析是研究一个变量（因变量）与多个因子（自变量）之间非确定关系（相关关系）的最基本方法。它比只有一个变量进行预测或估计更有效、更符合实际。笔者结合四川嘉陵江桐子壕水电站大坝变形监测项目，探讨了多元线性回归在大坝变形监测数据分析中的应用。

1 多元线性回归分析

1.1 数学模型

多元线性回归分析是通过分析所观测的变形（效应量）和外因（原因）之间的相关性，来建立荷载-变形之间关系的数学模型［3］，其表达式如式（1）所示。

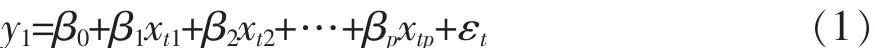
式中：下标t表示观测值变量，t=1，2，3，……n；p表示因子个数；εt～N（0，σ2）。

将式（1）用矩阵表示，结果如式（2）。

1.2 参数估计

由最小二乘原理可求得β的估值β，其结果如式（3）所示［4］。

1.3 分析方法及手段

目前，可以进行多元线性回归的软件较多。比如，利用 Excel中的 Linest函数、Mathlab中的Regress函数就可以很容易实现对监测数据的回归分析，并且可以在以上软件载体上进行程序的二次开发［5］，对监测数据进行批量处理，使监测数据处理工作变得简洁高效。

2 工程应用

四川省嘉陵江桐子壕水电站位于武胜县境内的嘉陵江干流上，枢纽主要由船闸、厂房、冲沙闸、泄洪闸等部位组成。该枢纽船闸水平位移主要采用三方边角交会法观测，大坝水平位移采用视准线（小角度法）观测，垂直位移采用一等水准法观测，各变形监测项目观测精度达到±1mm，观测精度较高。从大坝蓄水至今已运行近10年，观测数据较为齐全。大坝测点布置如图1所示。

图1 大坝测点布置图Fig.1 Dam monitoring point layout

2.1 模型建立

通常，影响坝体位移的主要因素是上、下游水位、坝体温度、时效。因此，位移的统计模型包括水压、温度和时效分量，如式（4）所示。

式中：δ为位移值；δH为水压分量；δT为温度分量；δθ为时效分量。

因运行期大坝的坝体温度取决于外界温度，且存在滞后现象，因此，坝体温度可用大气温度及其一系列“滞后”因子来表示［6］。

2.2 影响因子分析

在进行变形建模分析过程中，采用多元回归法计算，主要考虑了如下影响因子：（1）上游水位H0测值（H-H0）的1、2、3次方。（2）坝区气温T。选取前1、3、7、15、30、45、60、90、120、150、180 d平均温度测值。（3）时效。t、ln（1+t），其中t=t′／30，t′为测时日期距分析起始日期的时间长度，d。

2.3 监测数据的分析

采用多元回归分析法对大坝厂房段的监测数据（A01～A04）进行分析整理。大坝A01测点垂直位移监测数据回归成果如图2所示。

从图2可以看出，多元回归对监测数据拟合效果较好，并有效地对各影响因子进行了分离。温度升高，坝体膨胀，测点上移；温度降低，坝体收缩，测点下沉。水位上升，压力变大，测点下沉；水位下降，压力减小，测点上移。多元回归成功地分析出坝体测点变形机理，分析结果与大坝工程设计预期效果一致，并显示大坝时效因子的影响较小，坝体比较稳定［7］。

在以上分析结果的基础上，按式（5）对各因子所占比例进行计算（结果如表1所示），并找出影响大坝变形的主要因素。

式中：ai为某因子所占比例；xi为某因子的影响量值；x1+x2+x3为三影响值之和。

由表1中可以看出，温度是大坝变形的主要因素，时效因子的影响最小，复相关系数在0.55～0.91之间，剩余标准差在1mm左右。这说明，大坝回归效果较好，观测方法及观测精度较高［8］。

根据多元线性回归分析模型，对大坝第108期的监测数据进行预测，其结果如表2所示。

由表2可以看出，多元回归预报结果与实测值较为接近，对大坝的安全运行有很好的警示作用。

图2 测点A01垂直位移回归成果图Fig.2 Monitoring point A01 vertical displacement regression

表1 各分量所占比例及回归精度统计表T ab.1 Proportion of each part and regression precision statistics

表2 第108期监测数据预测统计表T ab.2 The 108th phrase monitoring data prediction statistics

3 结语

多元回归数据分析法相对较为成熟，且容易实现编程化，推广性较强。其不足之处表现为：对数据准确性要求较高，在使用之前应进行粗差处理。另外，当影响因子选择不当时，会对模型分析产生一定的干扰［9］。笔者认为，当前大坝数据分析模型种类繁多，模型复杂，理论性强而适用性差，当监测数据准确，影响因子选择明确的情况下，多元线性回归对大坝监测数据分析效果明显。

［1]赵斌，吴中如.水电自动化与大坝监测［J］.大坝观测与土工测试，2006（3）：18-21.

［2]王晓蕾，王其霞.逐步回归模型在大坝监测中的应用［J］.水科学与工程技术，2006（2）：60-62.

［3]黄伟朵，许昌.主成分回归分析在大坝安全监测中的应用［J］.水电自动化与大坝监测，2009（1）：57-59.

［4]黄声享，尹晖，将征，等.变形监测数据处理［M］.武汉：武汉大学出版社，2003：92-95.

［5]宋泽阳，李学创，齐文宇，等.矿井通风系统稳定性定量判定方法研究［J］.中国安全科学学报，2011（9）：119-124.

［6]黄自萍，范麟馨，沈建华，等.数值分析基础［M］.上海：同济大学出版社，2002：63-66.

［7]邹利.回归分析在大坝变形监测数据处理中的应用研究［J］.工程地球物理学报，2007（6）：644-647.

［8]鲁铁定，周世健，刘薇，等.大坝变形监测数据异常值检验与分析［J］.人民黄河，2009（12）：92-93.

［9]尹文怡，范通让.离散数据拟合模型的研究与实现［J］.计算机工程与应用，2008（31）：227-228.

[责任编辑 杨明庆]

TV698

B

10.13681／j.cnki.cn41-1282／tv.2017.01.005

2016-10-24

李 瑞 （1980-），男，湖北省枣阳人，工程师，主要从事测绘工程工作。