CASC2D模型与GSSHA模型在栾川流域的径流模拟

李致家，屈晨阳，黄鹏年，姚 成

(河海大学水文水资源学院，江苏 南京 210098)

CASC2D模型与GSSHA模型在栾川流域的径流模拟

李致家，屈晨阳，黄鹏年，姚 成

(河海大学水文水资源学院，江苏 南京 210098)

为研究半干旱半湿润流域复杂产流机制下不同模型结构对于径流模拟的影响，选取栾川流域为研究对象，在采用相同的DEM、土地覆盖以及土壤资料的前提下，利用基于超渗产流机制的CASC2D模型以及在其模型结构基础上改Green-Ampt方程为理查德方程计算下渗并增加地下水径流的GSSHA模型对1964—2000年间的8场洪水进行径流模拟。结果表明，GSSHA模型在栾川流域获得较好的模拟效果，除峰现时差外，GSSHA模型在洪峰、径流深模拟以及确定性系数方面均比CASC2D模型有较大提升。

分布式水文模型；CASC2D模型；GSSHA模型；半干旱半湿润流域；理查德方程；地下水径流；栾川流域

半干旱半湿润流域约占我国国土面积的1/3[1]，且主要位于北方地区。与单纯的湿润或干旱流域相比，半干旱半湿润流域的植被覆盖、地形等下垫面条件复杂，空间变异大，对于如何描述和模拟流域下垫面地理和水文特征空间变化的研究不足。此外，半干旱半湿润流域产流机制复杂，蓄满产流[2]与超渗产流并存，使得半干旱半湿润流域的洪水预报研究成为水文学研究的难点问题。在一个流域蓄满产流和超渗产流并存的情况下，应用较为广泛的水文模型主要有增加超渗产流的新安江模型[3-4]、半湿润流域蓄满超渗空间组合模型[5]、垂向混合产流模型[6]等，但是此类模型属于概念性模型，对降雨和下垫面条件空间分布不均匀给流域径流造成的影响考虑不足。随着地理信息技术以及遥感技术的发展，分布式水文模型逐渐显示出它的理论意义和具有挑战性的应用价值[7]，可以体现水文过程、输入、边界条件以及流域几何特征的空间异质性[8]的特点以应对半干旱半湿润流域的复杂情况。

笔者选取基于超渗产流机制的分布式水文模型CASC2D模型[9]及基于CASC2D模型改进的GSSHA模型[10]，将其应用于半干旱半湿润的栾川流域，研究在超渗模型结构中通过采用理查德方程以及添加地下水径流的方法模拟半干旱半湿润流域的产汇流过程并与实际的流量过程进行比较，为半干旱半湿润流域防洪、水资源管理、水土流失防治等问题的解决提供借鉴。

1 模 型 介 绍

1.1 CASC2D模型

CASC2D模型为科罗拉多州大学的P. Julien教授开发的分布式水文模型，模型由C语言编写，以DEM为基础提取水系及划分计算栅格单元。降雨扣除截留等初始损失后采用Green-Ampt方程[11]计算每个栅格单元的下渗率和累积下渗量。模型采用霍顿坡面流机制，降雨强度大于下渗率时，栅格单元上积聚的雨量向较低的栅格流动，并沿坡面汇集，经河网汇流到达流域出口断面[12]。

1.1.1 产流计算

在研究流域范围内利用雨量资料，采用基于距离平方倒数的降雨空间插值方法来估算整个流域的降雨强度分布。

自然流域内往往存在植被覆盖区域，植物叶子表面张力吸附部分降雨使其未降落到地面，该部分雨量不参与下渗计算。在CASC2D模型的计算栅格中，降雨量首先要满足植物截留量，直到累积降雨量达到植物截留量时才不扣除截留损失。不同的土地覆盖情况下植被截留量也不同，需要通过不同的土地利用分类确定截留系数。

CASC2D模型采用Green-Ampt方程作为模型下渗计算的基础结构，对土壤下渗率和累积下渗量进行近似计算。考虑到下渗计算的空间差异性，模型对流域上的每一个栅格单元都计算相应的下渗率，涉及的计算参数包括饱和土壤水力传导度、毛管水头和土壤缺水量等由每个栅格的土壤类型确定。

1.1.2 汇流计算

在CASC2D模型中，采用二维显式扩散波差分法来描述坡面汇流[13]。坡面水流从高处向低处汇流至河道，在水平面上流向分为2个方向，描述地面径流的控制方程采用的是基于圣维南的连续方程和动量方程，利用这2个公式，运用显式有限差分扩散波法来计算地面径流。河道汇流计算采用一维显式扩散波公式，水流控制方程为一维明渠水流的连续方程，流量计算采用曼宁公式。

1.2 GSSHA模型

GSSHA(gridded surface/subsurface hydrologic analysis)模型全称为栅格化地表/地下水文分析模型，是由美国陆军工程研发中心的水文学家Charles Downer以及美国怀俄明大学Fred Ogden教授在CASC2D模型基础上进行改进开发的基于物理基础的分布式水文模型。与CASC2D模型类似，GSSHA模型也是以DEM为基础提取水系及划分计算栅格单元，降雨、植被截留计算方法也相同。不同的是，考虑到土壤饱和与不饱和并存的情况，在计算每个栅格单元的下渗率和累积下渗量时，GSSHA模型采用的是理查德方程[14]。此外，GSSHA模型还添加了CASC2D模型结构中没有的地下水径流计算，采用的是承压水非稳定流运动基本微分方程，丰富了模型结构。下面主要介绍GSSHA模型的改进部分。

1.2.1 产流计算

在超渗产流机制占主导地位的流域，Green-Ampt方程计算简单，简化了下渗过程，且模拟结果可以达到预期效果，但在产流机制较为复杂的流域，Green-Ampt方程往往达不到预期的模拟精度。包气带中土壤水模拟是GSSHA模型的重要改进方面，为模拟包气带的水流运动情况，模型采用的是基于压力水头的理查德方程解决包气带一维垂向下渗过程[15]，公式为

(1)

式中：C——比水容量；Ψ——基模势，用毛管压力水头表示，cm；t——时间，h；z——垂直方向距离(向下为正)，cm；K——包气带水力传导度，cm/h；W——源汇项，cm/h。

由于K和C均是土壤含水量的函数，理查德方程是一个非线性微分方程。模型将每个栅格单元的土柱从地表开始离散化为A、B、C共3层；在计算下渗时，假设每一个时间步长内的K(Ψ)、C(Ψ)均为常数。方程离散化在空间上采用的是二阶隐式中心差分，在时间上则是一阶隐式前向差分。差分方程为

(2)

式中：Δt——时间步长，h；Δz——土柱深度，cm；i——纵向指数，代表土柱纵向中心单元；i-1——中心单元的上单元；i+1——中心单元的下单元；i-1/2——中心单元与上单元的边界；i+1/2——中心单元与下单元的边界；n——时间指数，代表当前时间段；n+1——下一时间段。

为线性求解理查德方程，假设同一个计算时段内的K和C为常数，通过每一层土柱顶部的下渗率计算公式为

(3)

式中：fi-1/2——土柱顶部下渗率，cm/h；Ki-1/2——土柱顶部水力传导度，cm/h；Ψi——土柱中心单元基模势，cm；Ψi-1——土柱中心下单元基模势，cm；Δzi-1/2——边界土柱深度，cm。

当土壤含水量已知时，ψ的值可用土壤水分特征曲线确定，由此就可以计算出每一层土柱中的下渗率。

1.2.2 汇流计算

Pinder和Bredehoeft通过计算机对地下水模拟得出二维非承压含水层地下水流控制方程[16]。在GSSHA模型中，假设对角项可忽略，则方程可表示为

(4)

式中：x——纵向距离，cm；y——侧向距离，cm；Txx、Tyy——纵向与侧向导水系数，m2/s；h——水头，m；S——弹性储水系数；t——时间，s；W(x，y，t)——源汇项，m/s。

通过线性逐次超松弛迭代对式(4)进行五点隐式块中心有限差分[17]，得到包含纵向与横向的二维地下水流差分方程：

(5)

式中：Δx——纵向离散空间增量，m；Δy——横向离散空间增量，m；j——横向指数，代表土柱横向中心单元。

在模型的实际应用中，导水系数T由渗透系数Kgw与含水层厚度b的乘积表示，水头由地下水高程Ews代替。边界条件分为定水头条件及定流量条件。在定水头边界条件下，选择有河道流经的栅格单元中河道水面高程作为地下水模拟的特定水头边界条件；在定流量边界条件下，地下水与河道之间的流量交换利用达西定律计算。

2 流域概况及数据资料

选取栾川流域作为研究流域，栾川流域属于东湾流域的子流域，位于伊河河源地区，流域内有陶湾雨量站及栾川水文站，流域面积约340 km2。该流域属温带大陆性季风气候区，季节差异显著。多年平均降雨量744 mm，降雨时间分布不均，主要集中在7—9月。流域地势西高东低，上游森林覆盖率较高。2个模型采用的数据来源相同，数字高程资料来自于美国地质调查局提供的90 m×90 m DEM原始数据，土地利用数据来自于美国马里兰大学的全球土地覆盖数据库(GLCF)，采用的土壤资料为从中国科学院南京土壤研究所获得的1∶1 000 000数字化土壤属性资料。实测流量与实测雨量插值为1 h间隔，为了便于比较实测资料与模型模拟结果，径流模拟时段间隔取1 h。模型模拟计算步长均为6 s，为提高计算速度，模拟时将DEM转换为500 m×500 m精度，并在此基础上提取水系(阈值10 km2)。

3 结果与分析

CASC2D模型的参数率定时首先大致确定参数范围，再采用人工试错法调试参数，模型的敏感参数一般有饱和水力传导度、坡面糙率、毛管水头等。流域的模型参数见表1、表2。

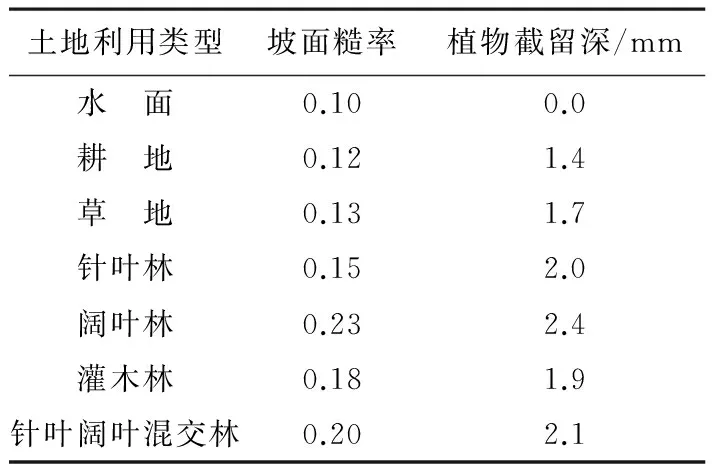
表1 栾川流域CASC2D模型土地利用参数值

注：各类型土地的覆盖管理因数皆为0.06，实践系数皆为1。

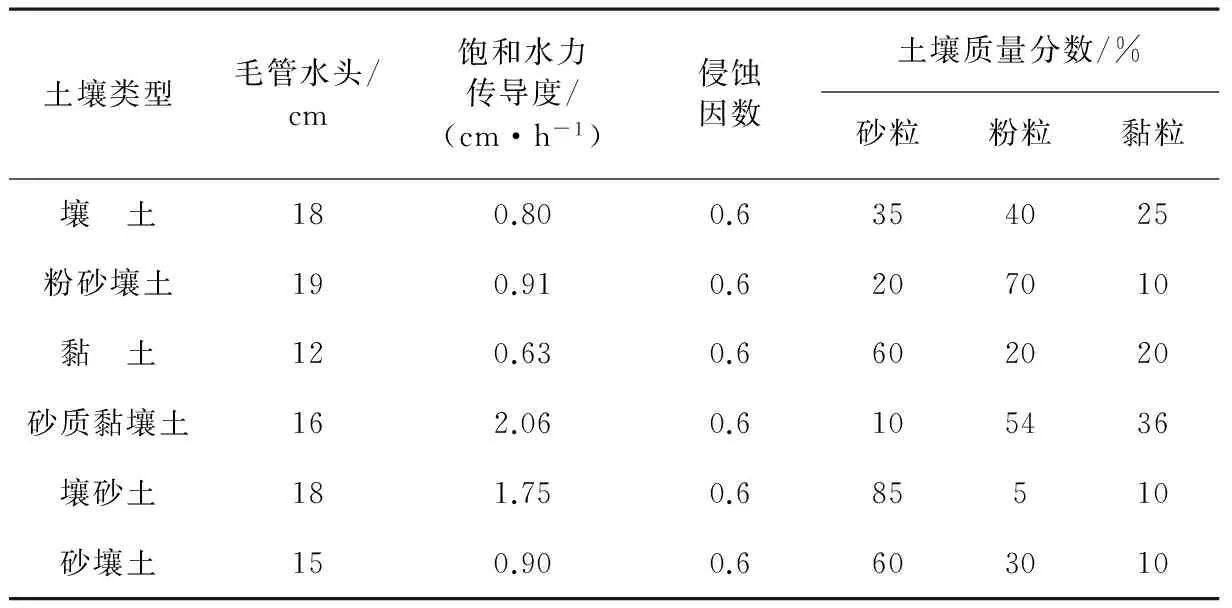
表2 栾川流域CASC2D模型土壤参数值

GSSHA模型中由于理查德方程的计算过程中土壤参数较多，同时模型还涉及地下水计算，模型的模拟参数较多。首先根据Rawls等[18]的研究成果大致确定土壤参数的取值范围，在参数率定过程中使用模型自带的SCE优化算法对模型参数进行率定，得到GSSHA模型的参数见表3、表4。

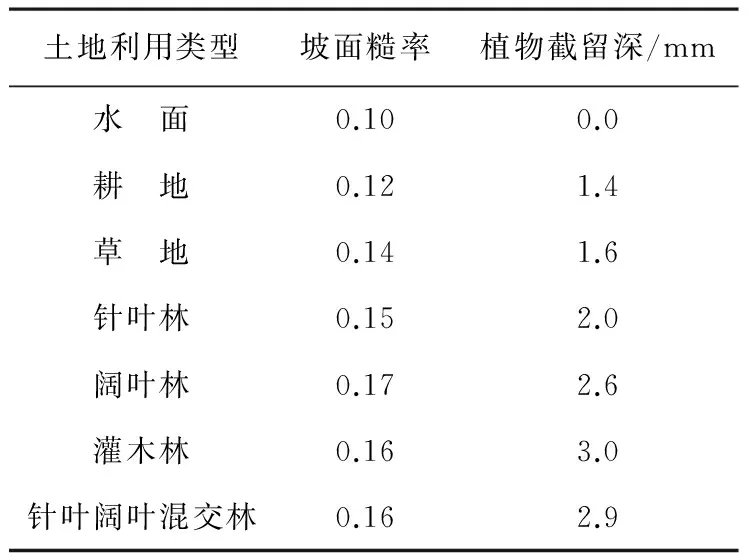
表3 栾川流域GSSHA模型土地利用参数值

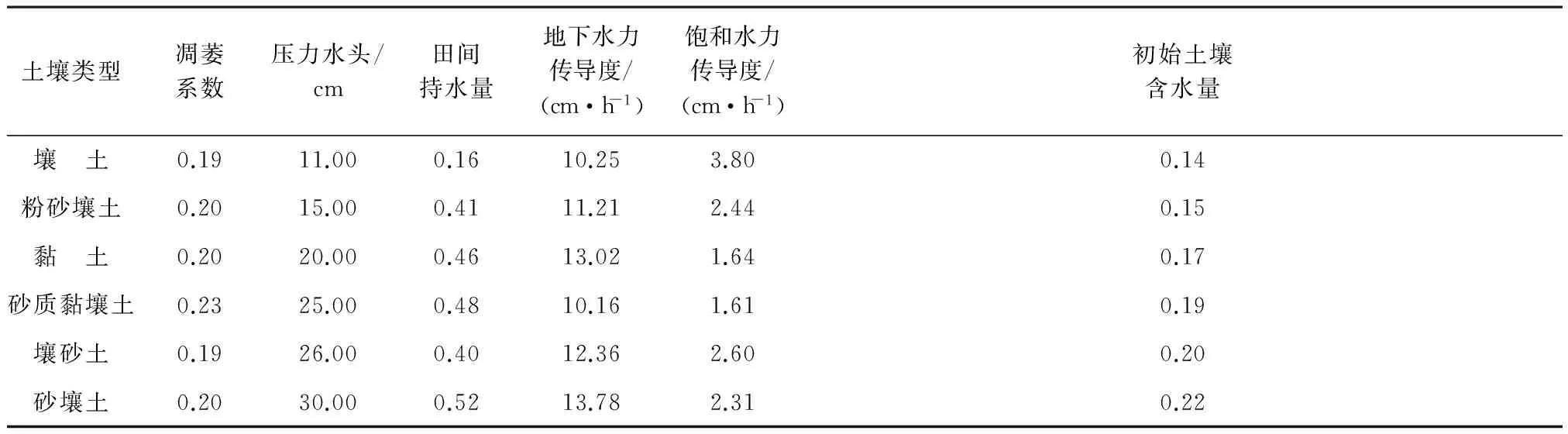
表4 栾川流域GSSHA模型土壤类型参数值

选取1964—2000年之间的8场洪水进行分别模拟，其中前5场为率定期、后3场为验证期。模拟结果见表5。图1为栾川流域1983100308号洪水模拟结果。

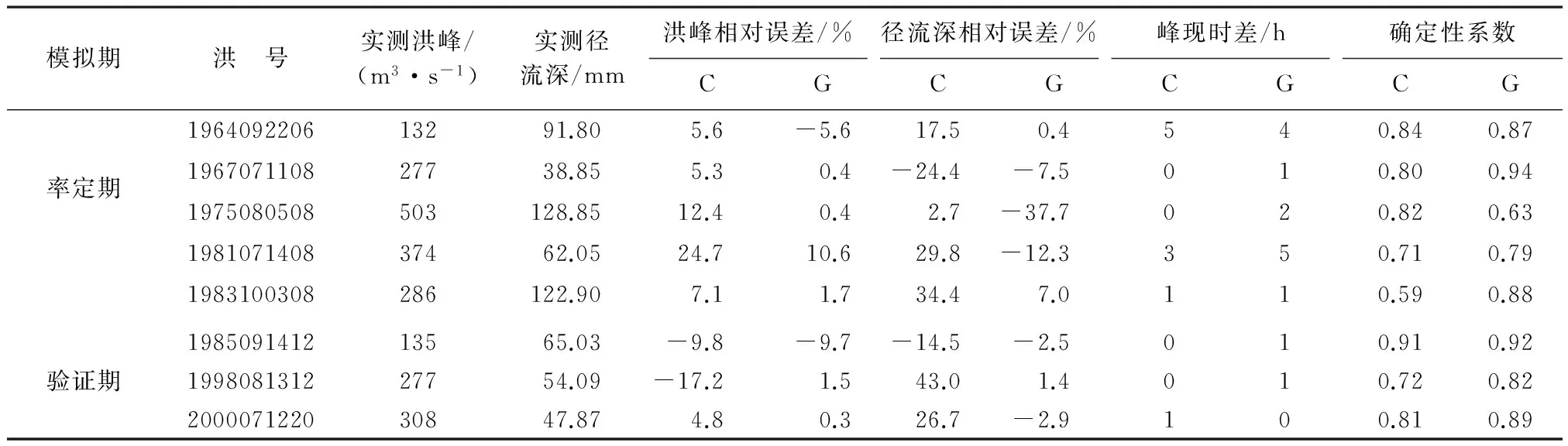
表5 栾川流域CASC2D模型与GSSHA模型模拟结果

注：C代表CASC2D模型，G代表GSSHA模型。

图1 栾川流域1983100308洪水模拟结果Fig. 1 Simulation results of Flood 1983100308 in Luanchuan Basin

从表5来看：(a)CASC2D模型洪峰误差只有1场超过20%，合格率为87.5%；GSSHA模型的洪峰合格率则达到了100%。(b)CASC2D模型的径流深模拟只有3场合格，合格率为37.5%；GSSHA模型径流深模拟只有1场不合格，合格率为 87.5%。(c)CASC2D模型的峰现时间合格率为87.5%，GSSHA模型的峰现时间合格率为75%。(d)2个模型的确定性系数均只有1场低于0.70，合格率均为87.5%。总体来看，在栾川流域GSSHA模型的模拟效果优于CASC2D模型的模拟效果。

比较图1所示2个模型的模拟结果，对结果进行分析如下：

a.从模拟整体效果上看，GSSHA模型的模拟结果明显优于CASC2D模型。CASC2D模型的模拟流量过程线呈现陡涨陡落的趋势，这是因为模型采用的是超渗产流机制，下渗公式为Green-Ampt方程，在模型结构中没有考虑壤中流，前期降雨扣除截留损失之后主要形成地面径流经坡面及河网汇集到出口断面，汇集速度快，汇流时由于忽略地下水使得落水阶段明显速度很快；GSSHA模型考虑了壤中流，采用理查德方程计算下渗，同时考虑了饱和与非饱和的情况，且在模型结构中增加了地下水径流，落水阶段与CASC2D模型相比均趋于平缓，与实测流量过程线也更吻合。

b.从洪峰模拟结果来看，GSSHA模型优于CASC2D模型。从径流深模拟结果来看，CASC2D模型不合格的5场洪水中有4场均为模拟结果偏小，这是由于模型没有考虑地下水径流。与此相比，考虑了地下水径流的GSSHA模型径流深模拟结果合格率则明显提高，8场洪水中只有1场未合格。

c.与CASC2D模型相比，GSSHA模型的峰现时间模拟结果较差。GSSHA模型中影响峰现时间的主要参数为河道糙率，为体现流域的实际情况，模型模拟过程中各个河段糙率均取不同值，且河道糙率同样对洪峰流量有影响，减小峰现时差的同时可能会影响模拟洪峰值，使得峰现时间的模拟结果不理想。

d.GSSHA模型虽然考虑了地下水径流，但是从图1中的10月6日8：00起可以明显看到退水速度有些加快，这可能是因为在模型计算地下水径流时需要输入流域的地下水位以及含水层高程数据，但由于实测资料的限制，只获得流域中部分站点的地下水位资料，无法完全体现整个流域的地下水位以及含水层高程的分布情况，这对整个流域的地下水模拟来说存在着一定不足。

4 结 语

通过比较2个模型在栾川流域的模拟结果，发现GSSHA模型的模拟结果优于CASC2D模型。相比于CASC2D模型单一的超渗产流机制以及Green-Ampt方程，GSSHA模型采用理查德方程分层次计算下渗，并在模型结构中添加地下水径流，使模型的产汇流机理更加完善。研究结果表明GSSHA模型可以应用于半干旱半湿润流域的径流模拟，基本满足流域洪水的预报要求。但是由于计算时间的限制，模型采用了较低精度的DEM数据，并且地下水资料的缺乏也无法完整体现流域的地下水分布情况，这些因素的存在降低了水文模型的模拟精度，相信随着计算机技术、遥感、水文理论及观测技术的发展，复杂产流机制下的水文模型研究还有很大的发展前景。

[ 1 ] 李巧玲，李致家，陈利者，等.半湿润半干旱流域降雨径流关系及下垫面相似性[J].河海大学学报(自然科学版)，2015，43(2)：95-99.(LI Qiaoling，LI Zhijia，CHEN Lizhe，et al. Research on rainfall-runoff relationship and similarity of underlying surface in semi-humid and semi-arid basins[J].Journal of Hohai University(Natural Sciences)，2015，43(2)：95-99.(in Chinese))[ 2 ] 芮孝芳.产流模式的发现与发展[J].水利水电科技进展，2013，33(1)：1-6.(RUI Xiaofang.The discovery and development of runoff formation models[J].Advances in Science and Technology of Water Resources，2013，33(1)：1-6.(in Chinese))

[ 3 ] 李致家，孔祥光，张初旺，等.对新安江模型的改进[J].水文，1998，18(4)：19-23. (LI Zhijia，KONG Xiangguang，ZHANG Chuwang，et al. Improving Xin’anjiang Model[J].Journal of China Hydrology，1998，18(4)：19-23.(in Chinese))

[ 4 ] DENG Peng，LI Zhijia，XIE Fan.Application of TOPMODEL in Buliu River Basin and comparison with Xin’anjiang model[J].Water Science and Engineering，2008，1(2)：25-32.

[ 5 ] 李致家，黄鹏年，张永平，等.半湿润流域蓄满超渗空间组合模型研究[J].人民黄河，2015，37(10)：1-6，34. (LI Zhijia，HUANG Pengnian，ZHANG Yongping，et al. Study on spatial combination model of infiltration-excess and saturation-excess runoff in semi-humid watersheds[J].Yellow River，2015，37(10)：1-6，34.(in Chinese))

[ 6 ] 包为民，王从良.垂向混合产流模型及应用[J].水文，1997，17(3)：18-21.(BAO Weiming，WANG Congliang. Vertically-mixed runoff model and application[J].Journal of China Hydrology，1997，17(3)：18-21.(in Chinese))

[ 7 ] 邓鹏，李致家. 3种水文模型在淮河息县流域洪水模拟中的比较[J].河海大学学报(自然科学版)，2013，41(5)：1-6.(DENG Peng，LI Zhijia. Comparison of three hydrological models in flood simulation for Xixian Basin of Huaihe River[J].Journal of Hohai University(Natural Sciences)，2013，41(5)：1-6.(in Chinese))

[ 8 ] 徐宗学，程磊.分布式水文模型研究与应用进展[J].水利学报，2010，41(9)：1009-1017.(XU Zongxue，CHENG Lei. Progress on studies and applications of the distributed hydrological models[J].Journal of Hydraulic Engineering，2010，41(9)：1009-1017.(in Chinese))

[ 9 ] DOWNER C W，OGDEN F L，MARTIN W D，et al. Theory，development，and applicability of the surface water hydrologic model CASC2D[J].Hydrological Processes，2002，16：255-275.

[10] DOWNER C W，OGDEN F L. GSSHA：model to simulate diverse stream flow producing process[J].Journal of Hydrologic Engineering，2004，9(3)：161-174.

[11] GREEN W H，AMPT G A. Studies on soil physics[J].Journal of Agricultural Science，1911，4(1)：1-24.

[12] JOHNSON B E，JULIEN P Y，MOLNAR D K，et al. The two-dimensional upland erosion model CASC2D-SED[J].Journal of the American Water Resources Associaation，2000，36(1)：31-42.

[13] JULIEN P Y，SAGHAFIAN B. CASC2D user manual-a two dimensional watershed rainfall-runoff model[M].Fort Collins：Colorado State University，1991.

[14] RICHARDS L A. Capillary conduction of liquids through porous mediums[J]. Journal of Applied Physics，1931，1(5)：318-333.

[15] HAVERKAMP R，VAUCLIN M，TOUMA J，et al. A comparison of numerical simulation models for one-dimensional infiltration[J]. Soil Science Society of America Journal，1977，41(2)：285-294.

[16] PINDER G F，BREDEHOEFT J D. Application of the digital computer for aquifer elevation[J].Water Resources Research，1968，4(5)：1069-1093.

[17] DOWNER C W，OGDEN F L. Gridded surface subsurface hydrologic analysis (GSSHA) user’s manual (version 1.43 for watershed modeling system 6.1) [M]. Washington，DC：U.S. Army Corps of Engineers，2006.

[18] RAWLS W J，BRAKENSIEK D L，SAXTON K E. Estimation of soil water properties[J]. Transaction of the ASAE，1982，25(5)：1316-1320，1328.

Simulation of runoff in Luanchuan Basin using CASC2D and GSSHA models

LI Zhijia，QU Chenyang，HUANG Pengnian，YAO Cheng

(CollegeofHydrologyandWaterResources，HohaiUniversity，Nanjing210098，China)

In order to investigate the influence of different model structures on runoff simulation in semi-arid and semi-humid basins with complex runoff generation mechanisms，the CASC2D model and GSSHA model were used to simulate eight flood events from 1964 to 2000 in the Luanchuan Basin using the same digital elevation model (DEM) data，land cover data，and soil data. The CASC2D model is based on the excess-infiltration mechanism，and the GSSHA model is based on the CASC2D model through addition of groundwater runoff and transformation of the Green-Ampt equation into the Richards equation to calculate the infiltration. The runoff simulation results show that the GSSHA model performs well in the Luanchuan Basin. Compared with the CASC2D model，the simulation of flood peak，runoff depth，and the deterministic coefficient are highly improved by the GSSHA model except for peak time error.

distributed hydrological model；CASC2D model；GSSHA model；semi-arid and semi-humid basin；Richards equation； groundwater runoff； Luanchuan Basin

10.3876/j.issn.1000-1980.2017.01.001

2016-05-25

国家自然科学基金(41130639, 51179045)；水利部公益性行业科研专项(201501022,201401034)

李致家(1962—)，男，山西运城人，教授，博士，主要从事水文预报与流域水文模型研究。E-mail：zhijia-li@vip.sina.com

P33

A

1000-1980(2017)01-0001-06