Dirichlet级数关于p-准确级的型
2017-02-11吴世玕
吴世玕
(江西理工大学 理学院, 江西 赣州 341000)
Dirichlet级数关于p-准确级的型
吴世玕
(江西理工大学 理学院, 江西 赣州 341000)
讨论Dirichlet级数及随机Dirichlet级数所表示的整函数关于p-准确级的型(下型)与系数和指数的关系,给出了型和下型的取值范围为αp≤T≤αpeρDrp,βp≤x≤eρDrp。
Dirichlet级数; 随机Dirichlet级数; 准确级; 型函数; 型; 下型
MR subject classification: 30K10
自Valiron G与Hiong K分别引入有限级和无限级的型函数[1-2]后,学者们在研究整函数、亚纯函数、解析函数的增长性质时,常结合型函数,考虑关于准确级的型、下型[3-5]。函数的增长级中用得较多的是Ritt级、p-级、(p,q)(R)级、对数增长级、相对(p,q)级等[6-10]。
设Dirichlet级数
(1)
满足
{an}⊂C,0<λn↑∞,s=σ+it,

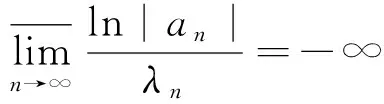
(2)
其中σ、t为实变量,则级数(1)在全平面上收敛。即f(x)为整函数。

在文献[7,11-12]中引进Dirichlet级数p-级ρ的定义为
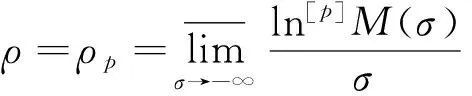
(3)
其中p=2,3,…,且ln[0]x=x,ln[k]x=ln(ln[k-1]x)。
设ρ∈(0,+∞),本文仿照文献[13],引进分段连续可微函数ρ(r),其在r≥r0(r0>0)上单调增加,且满足

(4)
令t=U(r)=rρ(ln r)(r>0),并设r=W(t)是t=U(r)的反函数,则有

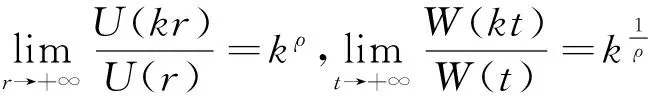
(5)
称U(r)为f(s)的型函数,称ρ(r)为f(s)的p-准确级。令

(6)
分别称T、χ为f(s)关于p-准确级ρ(r)的型和下型,其中p≥2。
文献[12]利用型函数的反函数刻画了T、χ的范围,对于下型,只给出了p=2时的结论。型函数U(r)=rρ(ln r)是单调增加的幂指函数,理论上存在反函数,若ρ(r)不是常值函数,则反函数很难求出,或根本无法求出反函数的解析表达式。本文直接用型函数刻画Dirichlet级数及随机Dirichlet级数关于p-准确级ρ(r)的型和下型T、χ的范围。
1 Dirichlet级数关于p-准确级的 型、下型
引理1 设a、b是正数,ln[p-3]b>0,则函数φ(x)=exp[p-2][aU(ex)]-bx的最小值点x0满足
(7)
且最小值
(8)
其中
exp[0](x)=x,exp[1](x)=exp(x),
exp[k](x)=exp(exp[k-1](x))。
引理2 设a>0,则ψ(x)=x[a-ln(W(ln[p-2]x))]的最大值点x0满足
(9)
最大值
(10)
用求导的方法及(4)、(5)式,就可证明引理1和引理2的结论。
定理1 设级数(1)满足条件(2),其p级ρ∈(0,+∞),记
(11)
则αp≤T≤αpeρD。
证明 (1)当T<+∞,p≥3时, ∀ε>0,∃σ′>0,当σ>σ′时
ln|an|≤lnM(σ)-λnσ≤exp[p-2][(T+ε)U(eσ)]-λnσ。
(12)
由引理1知

所以

从而
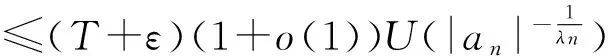
故T+ε≥αp。由ε的任意性知,T≥αp。
下面证明T≤eρDαp。
不妨设αp<+∞。于是,∀ε>0,存在常数A>0(A代表一个正数常数,不同的表达式中,A的取值可以不同)使得∀n≥1有

(13)
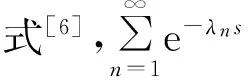

从而
lnM(σ)≤ln(AB(ε))+

σ→+∞时,由引理2得
(1+o(1))eρ(D+ε)(αp+ε)U(eσ),所以T≤eρ(D+ε)(αp+ε)。由ε的任意性知,T≤eρDαp。
(2)当T=+∞,p≥3时,若αp<+∞,则由上面推理知,T≤eρDαp仍然成立,此与T=+∞矛盾,所以,αp=+∞。
(3)当T≤+∞,p=2时,定理1结论也成立[14]

(14)
(15)
则βp≤χ≤eρDγp,其中{n(σ):σ∈R}={n(σk)}是f(s)的主要指标序列[6],{σk}是n(σ)的间断点序列。
证明 (ⅰ)当p≥3时,设{nk}↑∞,ln[p-2]λnk~ln[p-2]λnk+1,k→∞,记
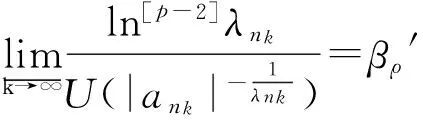


从而
lnM(σ)≥ln|ank|+λnkσ≥
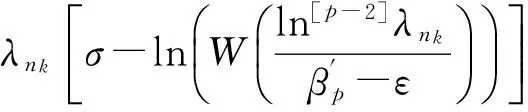
取σk>ε,使

(16)
则σk↑+∞,∀σ∈(σk,σk+1),





由于{nk}是符合(14)式的任一自然数子序列,所以χ≥βp。
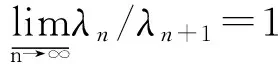
下面证明χ≤eρDγp。

记

先证χ′≤eρDγp。不妨设0<χ′<+∞,则∀ε>0,当σ充分大,且σ∈(σk-1,σk]时,n(σ)=n(σk)。
ln|an(σk)|=lnm(σ)-λn(σk)σ≥
exp[p-2][(χ′-ε)U(eσ)]-λn(σk)σ。
由引理1知
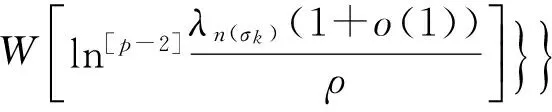
所以
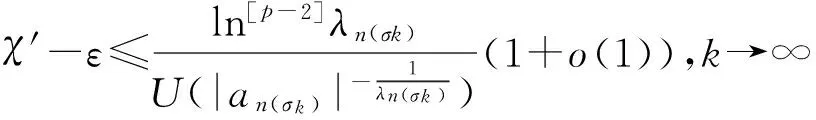
故χ′-ε≤γp。若χ′=+∞,则用任意大的正数X代替χ′-ε,一样可证明X≤γp,从而γp=+∞。由ε任意性知χ′≤γp。
类似于文献[6]可以证明,∀ε>0,存在与f、ε有关的正常数K(ε),使得
M(σ)≤K(ε)m(σ+D+ε),
(17)
所以
χ′eρ(D+ε)。
由ε的任意性及χ′≤γp知,χ≤χ′eρD≤γpeρD。
(ⅱ)当p=2时,证明过程与(ⅰ)相似,只是在证明过程中,取σk时,(16)式有点改变,使
即可。详细的证明过程从略。
2 随机Dirichlet级数关于p-准确级的型
设随机Dirichlet级数

(18)
{Xn(ω)}是概率空间(Ω,A,P)上独立的随机变量序列,E(Xn)=0,有有限方差

E(Xn/δn)=dn≥d>0,
{an}⊂C,{λn}↑∞ ,
且

(19)
则f(s,ω)是一个随机整函数[15]。设
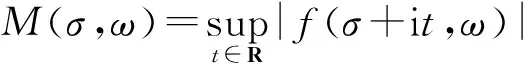

(20)

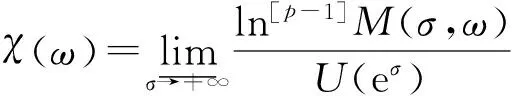
(21)
分别称T(ω)和χ(ω)为f(s,ω)的p-级准确型和下型。
定理3 设随机Dirichlet级数(18)满足条件:{Xn(ω)}是概率空间(Ω,A,P)上独立的随机变量序列,E(Xn)=0,有有限方差

E(|Xn|/δn)=dn≥d>0,
{an}⊂C,{λn}↑+∞,
且满足(19)式,U(r)是满足(4)式的型函数,则

其中,
(22)
证明 由文献[15]中的引理4和引理5容易证明,当n充分大时,
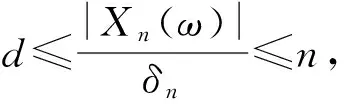
(23)
记
则当p≥3时,∀ε>0,有
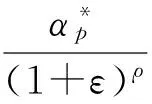

∀ε∈(0,1),有
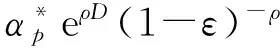

由定理1知,
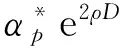
当p=2时,结论也成立[14]。
[1] VALIRON G. Fouctions entieres d′order fini et fouctions meromorples[M].Geneve: l′Enseignement Mathema-tique,1960.
[2] HIONG K. Sur les fouctions et let fouctions meromorphes d′ofdre infini[J].Journal de Mathématiques Pures et Appliquées, 1935,14:233-308.
[3] 高宗升.Dirichlet 级数表示的整函数的增长性[J].数学学报,1999,42(4):741-748.
[4] ZHANG X L. The precise order and singular directions of meromorphic functions[J].Journal of Beijing Institute of Technology, 1999,6(1):14-18.
[5] KONG Y Y,SUN D C. On Type-function and the growth of Laplace-Stieltjes transformations convergent in the right half-plane[J]. Advances in Mathematics, 2007,37(2):197-205.
[6] 余家荣,丁晓庆,田范基.Dirichlet级数与随机Dirichlet级数的值分布[M].武汉:武汉大学出版社,2004.
[7] 贺隆贞.关于狄里克莱级数确定的解析函数的P(R)级和P(R)型[J].数学杂志,1983,3(1):61-71.
[8] HE L Z.On the (p,q)(R) order and lower (p,q)(R) order of entire functions defined by Dirichlet series[J].Journal of Wuhan University, 1983,3:73-89.
[9] 陆万春,易才凤,漆勇方.Laplace-Stieltjes变换所确定的整函数的对数级[J].数学的实践与认识,2014,44(19):286-291.
[10] DIBYENDU B, SRIMANTA J.Meromorphic functions of relative order (p,q)[J].Soochow Journal of Mathematics, 2007,33(3):343-357.
[11] 孔荫莹.Dirichlet-Hadamard乘积的q-级和q-型[J].数学学报,2009,52(6):1165-1172.
[12] 许全华. Dirichlet级数所表示的整函数的(R)准确级的型[J].数学年刊,1986,7A(3):266-277.
[13] 庄圻泰.亚纯函数的奇异方向[M].北京:科学出版社,1982.
[14] 吴世玕,杜红霞.有限级Dirichlet级数及随机Dirichlet级数(R)准确级的型[J].江西理工大学学报,2009,30(3):66-69.
[15] 陈聚峰,刘名生.有限级Dirichlet级数及随机Dirichlet级数[J].数学物理学报,2005,25A(7):965-973.
〔责任编辑 宋轶文〕
The type of Dirichlet series ofp-proximate order
WU Shigan
(Faculty of Science, Jiangxi University of Science and Technology, Ganzhou 341000, Jiangxi, China)
The relationship between the type (lower type) of entire function represented by Dirichlet series and random Dirichlet series ofp-proximate order with their coefficient and index are discussed. The value range of type and lower type ofp-proximate are given thatαp≤T≤αpeρDrp,βp≤x≤eρDrp.
Dirichlet series; random Dirichlet series; proximate order; type function; type; lower type
1672-4291(2017)01-0001-05
10.15983/j.cnki.jsnu.2017.01.111
2015-10-26
国家自然科学基金(61364015)
吴世玕,男,副教授。E-mail:wusg64@163.com
O174.5
A
