初中学生几何推理能力的培养策略
2017-02-10刘侠南
刘侠南
(苏州吴江区松陵第一中学,江苏 苏州 215200)
初中学生几何推理能力的培养策略
刘侠南
(苏州吴江区松陵第一中学,江苏 苏州 215200)
逻辑推理贯穿初中几何教学的全过程,但初中生几何推理能力相对薄弱,主要表现在推理意识、推理严谨性不足。结合教学实际,从“培养学生几何推理意识和习惯、增强学生几何推理的严谨性、合情推理和演绎推理并重提升”三个方面来提升初中生几何推理能力。
初中数学;几何;推理能力;培养策略
逻辑推理能力是数学学科的基本思维能力,其主要内涵是具有正确性与合理性的思考能力。根据《初中数学课程标准》中的定义,逻辑推理能力包含三个层面内容,一是能通过观察、归纳及类比等手段形成数学猜想,在此基础之上,寻求证明或否定该命题;二是对整个数学思考过程进行清晰的表达,做到有理有据;三是能够就某一命题,用符合数学逻辑的语言与他人进行交流和讨论。
对初中阶段而言,几何内容的学习是初中数学知识体系的重要组成部分,也是训练和培养学生逻辑思维和推理能力的重要内容。在强调素质教育的背景下,数学教学越来越强调方法论的传授,让学生在掌握原理和方法的基础之上,自主进行探索,解决问题,而逻辑推理能力正是学生所要掌握的核心内容。初中数学课程中的几何学内容,都是以若干的公理、定理以及衍生出的各种几何性质为基础的,任何几何学问题的解决都要从这些核心的概念出发,而这样的解题过程也正是逻辑推理的重要路径。
多年的数学几何学教学实践,发现目前初中生几何推理能力相对较弱,如推理意识以及推理的严谨性不足等,因此探索提升初中生几何推理能力的有效路径具有普遍的意义。就初中生几何推理能力存在的问题以及相应的解决策略进行阐述。
一、几何推理能力存在的问题
1.几何推理意识和推理习惯较差
虽然对推理能力的要求涵盖了整个初中几何学教学过程,但初中生在几何推理意识和推理习惯上仍显得不足。
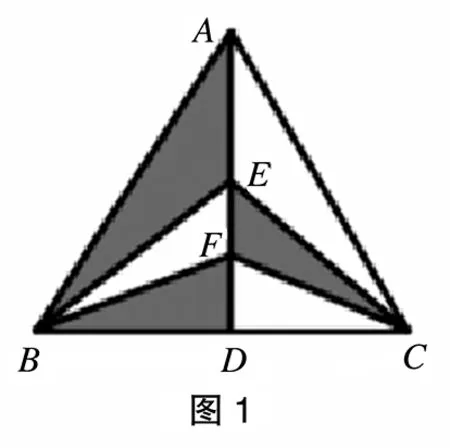
如图1,在△ABC中,AB=AC=5,BC=6,EF是中线AD上的两点,则图中阴影部分的面积是多少?对于这个题目,不少同学显得手足无措,认为不知道E、F是否是AD的等分点,不知道如何去解题,进而走入了死胡同,而推理意识较强,有较好推理习惯的同学会紧紧根据已知的条件,顺藤摸瓜,最终得到本题的答案。其中典型的推理过程如下:
根据AB=AC,可知△ABC为等腰三角形,而AD为中线,根据等腰三角形三线合一的性质可以知道,AD同样是△ABC在BC边的中线和高线。并进一步推导可知BD和DC(二者长度都为3)分别是△BDF、△BEF、△ABE以及△CDF、△CEF、△ACE的高线,根据已知的长度数据以及直角三角形的三边数值关系,不难得出结论,整个阴影面积为整个△ABC的一半(△ABD与△ACD面积相等),即6。
其实这个题目并不难,关键要养成几何推理的思维习惯,通过一步步推理很快就能得到正确答案。因此,从这个简单的习题可以发现,目前初中生的几何推理意识和习惯要进一步培养。
2.几何推理的严谨性不足
与此同时,严谨性不足也是初中生在进行几何推理中的普遍问题,由于推理能力要求思维的正确和合理性,因此严谨性不足是几何推理能力提升的重要障碍。比如习题:“直角三角形的三边长分别为2,3,m,则m的值为____?”对于该题,相信许多同学在学习过勾股定理这部分内容后,都会觉得很简单,但很多同学都只能给出一个答案,可以看到,学生们都知道勾股定理的公式,但是由于严谨性不足,直观地认为m所代表是直角边或者斜边,没有结合图形进行分类讨论,因此导致只能给出一个答案。
3.几何合情推理能力欠缺
在几何教学实践中发现,教材演绎推理占据了过多的篇幅,使得合情推理不为学生所熟知,几何合情推理能力较为欠缺。学生对于几何推理的认知往往局限于根据已有的条件,通过相应的公理、定理和性质通过推导得到结论。事实上,合情推理对于提升学生数学思维能力有重要作用。还是以图1中的习题为例,很多同学就算得到正确答案也都是通过演绎推理的方式,而事实上也有部分学生看到整个图形后,会猜想阴影部分面积很可能是整个△ABC的一半。大致的思维过程如下:
通过观察,直观的感觉会让我们猜想△BEF和△CEF的面积相等,如果真相等,那阴影部分面积很可能是△ABC的一半。对于这种猜想可以进行验证,根据所给的条件,AB=AC=5,AD为中线,BC=6等,我们通过一步步分析也能得到正确答案,事实上,在有限的时间情况下,这种方法能够更快得到结果。
合情推理其实对学生想象力、观察力有着较高的要求,而现在初中生在这方面比较欠缺,因此在几何学习中,也就表现在其几何合情推理能力存在不足。
二、几何推理能力的培养策略
1.培养学生几何推理意识和习惯
针对初中学生几何推理意识和习惯的不足,首先要加强学生对几何基础知识的掌握,尤其是公理、定理以及相应性质的认知和灵活运用,只有基础打的牢固,几何推理过程才能做到有理有据。其次,几何推理能力的形成也需要教师的引导,教师在进行几何学教学过程中,要加强对学生推理过程的梳理,让学生在潜移默化中形成几何推理的模式和习惯。与此同时,大量的习题练习也是有必要的,需要注意的是教师在选题时要选择有典型意义的题目,通过强化练习,对学生尚不稳定的推理意识加以巩固。
2.增强学生几何推理的严谨性
在初中生养成良好的几何推理意识的基础之上,严谨性的提升也是加强学生几何推理能力的重要一环。首先教师要以身作则,在教学实践中,对于几何问题的讲授过程中要思维缜密,做到有理有据,让学生在潜移默化中加强对严谨思维逻辑的认识。
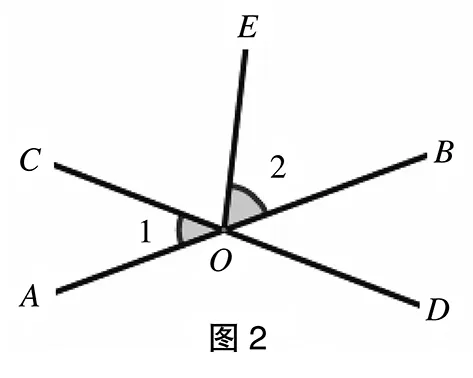
如图2,直线AB和直线CD相交于点O,∠1=47°,∠2=53°,则∠EOD的度数是多少?该问题其实很简单,但是教师在讲授过程中,几何推理的严谨性不可缺。
因为直线AB与直线CD相交于O,∠AOC和∠BOD是对顶角
所以∠1=∠BOD=47°
又因为∠EOD=∠2+∠BOD
所以∠EOD=∠2+∠1=100°
很多同学遇到此类题目,会直接写∠EOD=∠2+∠1
=100°,虽然也得到正确答案,但是最基本的严谨性丢失了。初中生接触的几何学知识属于最基础的内容,这就要求学生更加重视基本方法的掌握,只有构建起严密严谨的推理思维,才能更进一步探索几何的奥秘。
3.合情推理和演绎推理并重提升
几何合情推理能力的提升关键在数学教师的引导,教师首先要认识到合情推理能力在初中生几何学习中的重要作用,在教学实践中有意识地提升合情推理能力的训练。
例如,在研究中点四边形时,可以设计以下问题:
(1)连接平行四边形的各边中点所得的四边形是什么四边形?
(2)连接矩形的各边中点所得的四边形是什么四边形?
(3)连接菱形的各边中点所得的四边形是什么四边形?
(4)连接正方形的各边中点所得的四边形是什么四边形?
(5)连接任意四边形的各边中点所得的四边形是什么四边形?
(6)中点四边形和原四边形的哪些线段的性质有关系?
(7)你能证明上述结论吗?
通过画一画、量一量等方式亲身探索,学生可以容易地得出结论,并且进一步通过证明,可以体验从特殊到一般,从感性到理性的思维过程,通过这种锻炼,无形中学生的合情推理意识和能力也得到了提升。
三、结论
推理能力提升是几何课程学习中的重要目标,对于初中生数学思维的提升有重要意义。目前,初中生几何推理能力仍存在一些问题,主要表现在推理意识不足、推理严谨性欠缺以及合情推理能力较低等方面。针对以上问题,要认识到制约推理能力提升的关键因素,有针对性进行解决,逐步提升初中生几何推理能力。
[1]孙瑞.初中几何演绎推理能力培养的实践研究[D].长沙:湖南师范大学,2015.
[2]童振华.破解初中几何推理困难的多种思路[J].科学大众(科学教育),2016(1):14—15.
[3]孙金栋,吴敏.初中数学“图形与几何”中学生合情推理能力的培养[J].科技信息,2011(9):176+299.
[4]冯清汁.浅谈初中几何推理入门教学[J].学周刊,2011(20):24.
〔责任编辑:李海波〕
10.3969/j.issn.1008-6714.2017.01.042
2016-10-12
刘侠南(1984—),女,江苏苏州人,中学一级,从事初中数学教学研究。
G633.63
1008-6714(2017)01-0089-02
