基于三剪统一强度准则的厚壁圆筒自增强分析

曹雪叶 赵均海 张常光长安大学建筑工程学院，西安，710061

基于三剪统一强度准则的厚壁圆筒自增强分析

曹雪叶 赵均海 张常光
长安大学建筑工程学院，西安，710061

基于三剪统一强度准则，考虑材料应变强化效应、包辛格效应、拉压异性及中间主应力的影响，采用双线性强化材料模型对厚壁圆筒进行自增强分析，得到了厚壁圆筒加载应力、残余应力和工作应力的解析解，提出了最佳自增强压力的计算方法，探讨了拉压比、强度准则变化参数的影响，比较了自增强处理和非自增强处理及双线性强化模型和理想弹塑性模型厚壁圆筒的应力分布差异。研究结果表明：厚壁圆筒的最佳自增强压力随半径比和强度准则参数的增大而增大；工作时的最大等效应力随半径比和强度理论参数的增大而减小，随拉压比的增大而增大；自增强等效应力的最大值在弹塑性分界面处，且应力沿壁厚的分布较均匀；与理想弹塑性模型相比，双线性强化模型所对应的弹塑性分界面半径和残余应力较小，且随着自增强压力的增大，两种模型的差值越来越大；等效应力随半径比的变化规律可为厚壁圆筒选择合理的壁厚提供一定的参考；自增强技术可改善厚壁圆筒工作时的实际应力分布，提高其极限承载能力。

厚壁圆筒；三剪统一强度准则；自增强分析；双线性强化模型；等效应力

0 引言

自增强是指在压力容器投入使用之前先进行加压处理，使其产生弹塑性变形后卸载以产生预加应力，从而减小容器工作时的整体应力，提高承载能力的方法[1]。在石油化工设备、压力容器、高压管道等设备的制造及使用中，常采用自增强技术改善其工作时的实际应力分布，提高其承载能力和疲劳寿命[2]。高压和超高压容器常采用高强钢等材料，这些材料的拉压性能有一定的差异，且存在应变强化和包辛格效应[3-4]。

目前，对厚壁圆筒自增强分析的代表性研究有：林太清等[5]基于三剪统一强度准则推导得到厚壁圆筒极限承压的统一解，但未考虑材料的应变硬化和包辛格效应；钱凌云等[6]采用双线性材料模型，基于von Mises屈服准则建立了厚壁圆筒自增强理论模型，但未考虑材料的拉压异性及中间主应力的影响；马景槐[7]应用双剪统一强度理论，考虑材料屈服强度不同，对承受内压的线性强化厚壁圆筒进行了自增强分析，但双剪统一强度理论在某些特定应力状态下存在双重滑移角问题。三剪统一强度准则考虑了材料拉压强度不同及中间主应力影响，并克服了双剪统一强度理论的双重滑移角问题，在众多工程问题中得到较广泛的应用[8-9]。

本文基于三剪统一强度准则，考虑材料拉压异性(SD效应)及中间主应力的影响，采用双线性强化材料模型对厚壁圆筒进行自增强分析。

1 双线性强化材料厚壁圆筒基本方程

1.1 双线性强化模型

设厚壁圆筒的内径为ra，外径为rb，受均匀内压pa作用，圆筒内任意一点受径向应力σr、环向应力σθ、轴向应力σz共同作用，处于复杂应力状态。假设厚壁圆筒轴向受约束且变形很小，可将其简化为平面应变问题，其平衡方程为

(1)

几何方程为

(2)

式中，u为径向位移。

采用考虑材料应变强化效应和包辛格效应的双线性强化模型[6]，其本构关系如图1所示。图中，σst0、σsc0分别为初始拉伸屈服极限、初始压缩屈服极限；m、n分别为拉伸强化模量系数、压缩强化模量系数；E为弹性模量；α′为包辛格系数，α′=σsc0/σst0。

图1 双线性强化模型Fig.1 Bilinear hardening model

在强化条件下，屈服极限的数值与塑性变形强度有关。在单一曲线的假设下，拉伸屈服极限为[10]

σst=σst0(1+η εp)

(3)

(4)

式中，εp为有效塑性应变[11]；C为待定常数。

1.2 三剪统一强度准则

胡小荣等[12]通过考虑3个主剪面应力对的共同作用，建立了一个考虑材料SD效应和中间主应力的影响，同时还克服了双剪统一强度准则双重滑移角问题的新强度准则,即三剪统一强度。三剪统一强度准则的主应力表达式为

(1+b)(σ1-σ3)σst=(σ1-σ3)(σ1-ασ3)+b(σ1-σ2)(σ1-ασ2)+b(σ2-σ3)(σ2-ασ3)

(5)

强化条件下的加载屈服条件可表示为

(1+b)(σ1-σ3)σst0(1+η εp)=(σ1-σ3)(σ1-ασ3)+b(σ1-σ2)(σ1-ασ2)+b(σ2-σ3)(σ2-ασ3)

(6)

2 厚壁圆筒应力分析

2.1 弹塑性加载应力分析

厚壁圆筒在自增强压力pa作用下发生部分塑性变形，如图2所示。设rc为弹塑性分界面半径，则厚壁圆筒在rc≤r≤rb内为弹性变形，ra≤r≤rc内为塑性变形。

图2 厚壁圆筒力学模型Fig.2 Mechanical model of thick-walled cylinder

在弹性区(rc≤r≤rb)内，可将其看成内半径为rc，外半径为rb，承受内压pc作用的厚壁圆筒，其应力分量为[10]

(7)

由平面应变弹塑性问题的研究[13]可得轴向应力σz=(σr+σθ)/2。设σ1≥σ2≥σ3，则

(8)

在r=rc处即弹性区内表面刚开始进入塑性状态，该处的应力满足屈服条件且εp=0，将式(7)、式(8)代入式(6)整理可得

(9)

将式(7)、式(9)代入式(1)整理可得

(10)

将式(10)及r=rc处εp=0代入式(4)可得

(11)

在塑性区(ra≤r≤rc)内，由式(1)、式(6)、式(8)整理可得

(12)

将式(11)、式(12)代入式(4)可得

(13)

将式(13)代入式(12)积分可得

(14)

由弹塑性交界面处应力连续条件，即σr|r=rc=-pc，可得

(15)

将式(15)代入式(14)并利用屈服条件可求得塑性区的应力分量为

(16)

2.2 弹性卸载残余应力分析

实际自增强处理时，为避免出现厚壁圆筒卸载时反向屈服导致其承载压力减小的现象[6]，只允许发生弹性卸载情况。残余应力由弹塑性加载时的应力与弹性卸载时应力叠加求得，故自增强压力pa卸载后弹性区的残余应力为

(17)

塑性区的残余应力为

(18)

2.3 工作应力分析

厚壁圆筒工作时为弹性加载，不发生新的塑性变形。设工作压力为p，产生的应力由Lame公式求得:

(19)

厚壁圆筒的总应力由残余应力与工作应力叠加求得。由式(17)、式(19)可得弹性区(rc≤r≤rb)的总应力为

(20)

由式(18)、式(19)可得塑性区(ra≤r≤rc)的总应力：

(21)

3 自增强压力分析

3.1 自增强压力范围的确定

由式(9)、式(16)及内壁处的边界条件，即r=ra时σr=-pa，可得自增强压力pa与弹塑性分界面半径rc的关系为

(22)

(23)

(24)

式中，Hb为rc=rb时所求得的H值。

厚壁圆筒卸载时只考虑弹性卸载，考虑包辛格效应，其卸载的最大弹性极限为(1+α′)σst0，由式(9)可得弹性卸载时的最大自增强压力为

(25)

(26)

3.2 最佳自增强压力的求解

工作时的最大等效应力在弹塑性分界面处取得[6]，当该处的等效应力取最小值时，所确定的弹塑性半径和自增强内压可使工作时的应力分布最佳。基于三剪统一强度理论由式(20)可得弹塑性分界面处的等效应力为

(27)

4 算例分析及比较

取文献[6]中的算例：厚壁圆筒的工作压力p= 550 MPa，弹性模量E=210 GPa，泊松比ν= 0.3，包辛格系数α′=0.75，初始拉伸屈服极限σst0=1470 MPa，拉伸强化模量系数m=0.1，初始压缩屈服极限σsc0=1102.5 MPa。

4.1 算例分析

为验证本文方法的合理性，将本文计算所得最佳自增强压力与采用双剪统一强度理论在α=0.8时所得结果[7]进行对比分析，如表1所示。

表1 最佳自增强压力计算结果与文献[7]结果的比较Tab.1 Comparisons of optimum autofrettage pressure between calculations results and literatures results

由表1可知，采用本文方法计算的最佳自增强压力与文献[7]结果的比值范围为1.00～1.08，吻合良好，故三剪统一强度准则对厚壁圆筒的自增强分析具有良好的适用性；最佳自增强压力pa,opt随半径比rb/ra的增大而增大，也就是说随着壁厚增加，增大自增压力才能使厚壁圆筒达到最佳弹塑性状态；最佳自增强压力pa,opt随强度准则参数b的增大而增大，这是由于随着b的增大，所对应强度准则的极限面越大，厚壁圆筒达到屈服所需施加的压力也就越大。因此，对某种特定材料制成的厚壁圆筒，选取合适的强度准则对其自增强分析具有重要意义。

4.2 最大等效应力影响因素分析

采用本文方法可确定厚壁圆筒不同状态下的最佳弹塑性半径和最佳自增强压力，进而可求得厚壁圆筒工作状态下的最大等效应力。最大等效应力随半径比、强度准则参数及拉压比的变化规律如图3、图4所示。

图随rb/ra及b的变化规律(α=0.8)(α=0.8)

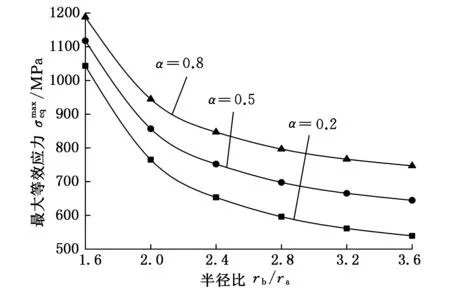
图随rb/ra及α的变化规律(b=0)(b=0)

由图3、图4可以看出，工作时的最大等效应力随半径比rb/ra的增大而减小，随拉压比α的增大而增大；最大等效应力随强度准则参数b的增大而减小，这是由于随着b的增大，中间主应力效应增大，材料的潜能得到更充分的发挥，从而使厚壁圆筒工作时的等效应力减小。从图3可知，当b=0时，半径比从1.6增大到2.4时，最大等效应力从1187.91 MPa减小到847.04 MPa，减小幅度为28.69%；半径比从2.8增大到3.6时，最大等效应力从796.52 MPa减小到747.02 MPa，减小幅度为6.21%，也就是说壁厚增大到一定程度时，增加壁厚不能明显改善其工作时的应力分布。因此，可根据等效应力随半径比的变化规律为厚壁圆筒选择较为合理的壁厚。由图4可知，α由0.2增大到0.8，半径比为1.6时，最大等效应力增大了144.92 MPa，增大幅度为13.89%；半径比为3.6时，最大等效应力增大了207.76 MPa，增大幅度为38.52%。故厚壁圆筒越厚，拉压比对其工作时的应力分布影响越大。

4.3 未自增强处理和自增强处理应力分布比较

为了研究自增强对厚壁圆筒实际应力分布的影响，本文对未自增强处理和自增强处理后厚壁圆筒工作时的应力分布进行比较，结果如图5所示。

图5 自增强处理和未自增强处理的等效应力分布比较Fig.5 Comparison of the equivalent stress distribution between autofrettaged and non-autofrettaged

由图5可得，未自增强处理时，厚壁圆筒等效应力在内壁处最大，等效应力由1492.50 MPa减小到717.27 MPa，减小幅度为51.94%；自增强处理后，等效应力的最大值在弹塑性分界面处，等效应力最大值为1187.90 MPa，最小值为1023.96 MPa且在内壁处，减小幅度为13.8%；故自增强处理使厚壁圆筒应力分布较均匀，在实际工程中可采用自增强技术改善其工作时的实际应力分布。由图5同样可以看出，未自增强处理时内壁处的应力为1492.50 MPa，已超过初始屈服极限1470 MPa，进入强化阶段；自增强处理后内壁处的应力为1023.96 MPa，还未达到初始屈服，处于弹性阶段。故自增强处理使厚壁圆筒的安全能力提高，在实际工程中可采用自增强技术提高其极限承载能力。

4.4 双线性强化模型和理想弹塑性模型比较

为了进一步分析应变强化效应和包辛格效应对厚壁圆筒自增强效果的影响，本文采用内径ra=50 mm，外径rb=80 mm的厚壁圆筒，比较分析双线性强化模型和理想弹塑性模型所对应的弹塑性分界面半径及等效残余应力，结果如图6、图7所示。

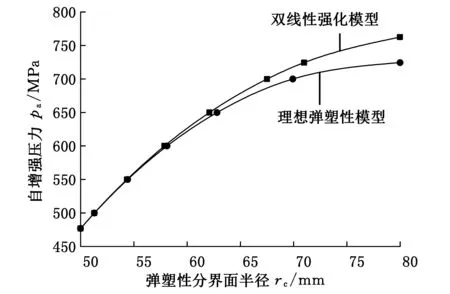
图6 分界面半径比较Fig.6 The radius comparison of the elastic plastic junction

图7 等效残余应力最大值比较Fig.7 Comparison of the maximum equivalent residual stress

由图6可知，双线性强化模型的自增强压力范围为476.96 MPa≤pa≤762.46 MPa；自增强压力为724.42 MPa时，理想弹塑性模型的厚壁圆筒已基本处于完全塑性状态，而此时双线性强化模型所对应的弹塑性分界面半径为70.99 mm，仍处于弹塑性状态；在同样的自增强压力下，双线性强化模型对应的弹塑性半径相对较小；随着自增强压力的增大，两种模型所对应的弹塑性分界面半径差值越来越大，这是由于自增强压力增大，厚壁圆筒塑性变形量增大，应变强化效应越明显，厚壁圆筒变形也就越困难。由图7可知，双线性强化模型厚壁圆筒的残余应力小于理想弹塑性模型的残余应力，且随着自增强压力的增大，两种模型残余应力相差越来越大。因此，考虑应变强化效应及包辛格效应可使厚壁圆筒的残余应力减小，进而使其工作时的实际应力分布更合理。

5 结论

(1) 本文采用双线性强化材料模型，基于三剪统一强度准则推导了厚壁圆筒加载应力、残余应力及工作应力的解析解，分析得到最佳自增强压力的计算方法。所得结果考虑了材料的应变强化效应、包辛格效应、SD效应及中间主应力的影响，可为厚壁圆筒的自增强技术提供一定的理论参考。

(2)厚壁圆筒的最佳自增强压力随半径比和强度准则参数的增大而增大；工作时的最大等效应力随半径比和强度准则参数的增大而减小，随拉压比的增大而增大；当壁厚增加到一定程度时，增加壁厚不能明显改善厚壁圆筒工作时的应力分布。该结论可为厚壁圆筒选择合理壁厚提供参考。

(3) 厚壁圆筒未自增强处理时，内壁处等效应力最大，进入强化阶段，且应力沿壁厚的变化较大；自增强处理后，弹塑性分界面处的等效应力最大，内壁处的等效应力处于弹性阶段，且应力沿壁厚的分布较均匀。故自增强处理使厚壁圆筒的安全储备提高，在实际工程中可采用自增强技术改善厚壁圆筒工作时的实际应力分布，提高其极限承载能力。

(4) 在同样的自增强压力下，双线性强化模型对应的弹塑性半径和残余应力相对较小，且随着自增强压力的增大，两种模型所对应的弹塑性分界面半径和残余应力的差值越来越大。因此，考虑应变强化效应及包辛格效应可使厚壁圆筒的残余应力减小，进而使其工作时的实际应力分布更合理。

[1] 曲文新, 古浪, 马利斌. 自增强外压球壳应力强度计算与分析[J]. 船舶工程,2015,37(10):98-101. QU Wenxin, GU Lang, MA Libin. Stress Calculation and Analysis of External Pressure Spherical Shell Based on Self-reinforced Technology[J]. Ship Engineering,2015,37(10):98-101.

[2] 郑小涛, 轩福贞. 热-机载荷下厚壁圆筒自增强压力与安全性分析[J]. 机械工程学报,2010,46(16):156-161. ZHENG Xiaotao, XUAN Fuzhen. Investigation on Autofrettage and Safety of the Thick-walled Cylinder under Thermo-mechanical Loadings[J]. Journal of Mechanical Engineering,2010,46(16):156-161.

[3] LIVIERI P, LAZZARIN P. Autofrettaged Cylindrical Vessels and Bauschinger Effect: An Analytical Frame for Evaluating Residual Stress Distributions[J]. Journal of Pressure Vessel Technology,2002,124(1):38-45.

[4] HUANG X P, CUI W C. Effect of Bauschinger Effect and Yield Criterion on Residual Stress Distribution of Autofrettaged Tube[J]. Journal of Pressure Vessel Technology,2006,128:212-216.

[5] 林太清, 胡小荣. 基于三剪统一强度准则的厚壁圆筒极限承压分析[J]. 福州大学学报(自然科学版),2006,34(5):727-731. LIN Taiqing, HU Xiaorong. Limit Pressures for Thick Wall Cylinders Based on the Triple Shear Unified Failure Criterion[J]. Journal of Fuzhou University(Natural Science),2006,34(5):727-731.

[6] 钱凌云, 刘全坤, 王成勇, 等. 厚壁圆筒自增强压力的优化分析[J]. 中国机械工程,2012,23(4):474-479. QIAN Lingyun, LIU Quankun, WANG Chengyong, et al. Optimization Analysis of Autofrettage Pressure for Thick Walled Cylinders[J]. China Mechanical Engineering,2012,23(4):474-479.

[7] 马景槐. 线性强化材料厚壁圆筒统一自增强分析[J]. 石油化工设备, 2003,32(3):26-30. MA Jinghuai. Autofrettage Analysis of Thick Wall Cylinder of Linear Strength Material Based on the Unified Strength Theory[J]. Petro-Chemical Equipment,2003,32(3):26-30.

[8] 李艳, 赵均海, 曹雪叶, 等. 内压作用下弯管爆破压力的三剪统一解[J]. 应用力学学报,2015,32(4):530-536. LI Yan, ZHAO Junhai, CAO Xueye, et al. Triple-shear Unified Solution for Burst Pressure of Elbows under Internal Pressure[J]. Chinese Journal of Applied Mechanics,2015,32(4):530-536.

[9] 张常光, 赵均海, 孙珊珊. 隧道围岩弹-脆-塑性应力的三剪统一解[J]. 应用力学学报,2012,29(5):530-534. ZHANG Changguang, ZHAO Junhai, SUN Shanshan. An Analytical Solution for Tunnel Stress in an Elastic-brittle-plastic Rock Based on the Triple-shear Unified Strength Criterion[J]. Chinese Journal of Applied Mechanics,2012,29(5):530-534.

[10] 徐秉业, 刘信声. 应用弹塑性力学[M].北京:清华大学出版社,1995. XU Bingye, LIU Xinsheng. Applied Elastic-plastic Mechanics[M]. Beijing: Tsinghua University Press,1995.

[11] 马景槐. 拉压异性强化材料高压容器自增强分析[J]. 石油化工设备,2001,30(2):1-4. MA Jinghuai. Autofrettage Analysis of High-pressure Vessel of Strength Material with Different Yield Strength in Tension and Compression[J]. Petro-Chemical Equipment,2001,30(2):1-4.

[12] 胡小荣, 林太清. 三剪屈服准则及其在极限内压计算中的应用[J]. 中国有色金属学报,2007,17(2):207-215. HU Xiaorong, LIN Taiqing. Triple-shear Yield Criterion and Its Applications to Limit Pressures for Thin and Thick Wall Cylinders and Thick Wall Spherical Shells[J]. The Chinese Journal of Nonferrous Metals,2007,17(2):207-215.

[13] 俞茂宏, 杨松岩, 刘春阳, 等. 统一平面应变滑移线场理论[J]. 土木工程学报,1997,30(2):14-26. YU Maohong, YANG Songyan, LIU Chunyang, et al. Unified Plane-strain Slip Line Field Theory System[J]. China Civil Engineering Journal,1997,30(2):14-26.

(编辑 袁兴玲)

Autofrettage Analysis of Thick-walled Cylinder Based on Triple-shear Unified Strength Criterion

CAO Xueye ZHAO Junhai ZHANG Changguang
School of Civil Engineering,Chang’an University, Xi’an, 710061

In order to analyze autofrettage theory of thick-walled cylinders, a bilinear hardening model was established and the analytical solutions of loading stresses, residual stresses and working stresses were derived based on the triple-shear unified strength criterion, which taken the strain hardening, Bauschinger effect, strength difference(SD) effect and the effect of intermediate principal stress into consideration. The optimal autofrettage pressure of thick-walled cylinder was deduced, the influences of ratio among tension stress and compression stress, strength criterion parameters were investigated respectively. In addition, the stress distributions of thick-walled cylinders between autofrettage and non-autofrettage, the bilinear hardening model and elastic-perfectly plastic model were compared. The results show that the optimum autofrettage pressure will increase with the increase of radius ratio and strength criterion parameter；the maximum equivalent working stress will decrease with the increase of radius ratio and strength criterion parameters, but increases with the increase of ratio between tension stress and compression stress; the maximum equivalent stresses in the elastic plastic junctions and the stresses of thick-walled cylinder along the wall thickness are well- distributed; compared with the elastic-perfectly plastic model，the radius of elastic plastic junction and residual stress of bilinear hardening model are lower, meanwhile with the increase of autofrettage pressure, the difference becomes more and more obvious; the curve of equivalent stress along with radius ratio may provide reference for choosing the optimal wall thickness; autofrettage technique may improve the working stress distribution and ultimate bearing capacity of thick-walled cylinders.

thick-walled cylinder; triple-shear unified strength criterion; autofrettage analysis; bilinear hardening mode; equivalent stress

2016-07-21

国家自然科学基金资助项目(41202191)；陕西省社会发展科技攻关项目(2015SF272)；长安大学优秀博士学位论文培育资助项目(310828150018)

TB125;TQ051.3

10.3969/j.issn.1004-132X.2017.01.013

曹雪叶，女，1989年生。长安大学建筑工程学院博士研究生。主要研究方向为强度理论及其应用。E-mail:caoxueye@126.com。赵均海，男，1960年生。长安大学建筑工程学院教授、博士。张常光，男，1982年生。长安大学建筑工程学院副教授、博士。