改进的模糊综合评价法在水资源承载力评价中的应用

袁艳梅,沙晓军,刘煜晴,高颖会,刘 俊

(1.河海大学水文水资源学院,江苏 南京 210098; 2.江阴市水资源管理办公室,江苏 江阴 214400)



改进的模糊综合评价法在水资源承载力评价中的应用

袁艳梅1,沙晓军2,刘煜晴1,高颖会1,刘 俊1

(1.河海大学水文水资源学院,江苏 南京 210098; 2.江阴市水资源管理办公室,江苏 江阴 214400)

用变异系数法及层次分析(analytic hierarchy process,AHP)法计算组合权重,并将灰色关联分析法中的灰关联系数应用于模糊综合评价模型中的模糊关系矩阵,结合定性、定量分析,对模糊综合评价模型进行改进。将改进后的模糊综合评价法应用于江阴市水资源承载力评价,结果表明,与传统模糊综合评价法相比,综合评价结果相同,但是计算结果对于各个评价等级的隶属度差距减小,降低了主观影响,说明改进后的评价方法在区域水资源承载力评价中应用良好。

模糊综合评价;组合权重;灰关联分析;水资源承载力

水资源承载力是指某个地区的水资源在一定的社会经济发展水平及保证水生态环境前提下,最大可承载的人口、社会经济和生态环境需求的能力[1]。由此可见,对水资源承载力进行评价可以揭示水资源可持续利用、社会经济发展和生态环境保护的关系,可以反映区域水资源开发利用情况,促进区域的社会经济建设与水资源保护同步进行。选择一种科学合理的评价方法评价并预测区域的水资源承载力,对区域的可持续发展具有重大意义

迄今为止,用于评价水资源承载力的方法有模糊综合评价法、主成分分析法、多目标情景分析法以及熵权法等[2-3]。由于水资源承载力具有不确定性和模糊性的特点,目前在水资源承载力评价方面应用最广泛的是模糊综合评价法。并且,为了使模糊综合评价模型应用更为广泛,评价结果更为准确,国内已经有不少学者提出了模糊综合评价模型的改进方法。2002年付强等[4]就提出了对模糊综合评判决策模型进行改进;2008年蒋金良等[5]在电能质量模糊综合评价模型中对隶属度函数进行了改进;刘力等[6-7]在2009年提出了将信息熵理论与模糊数学方法相结合,建立基于熵权的改进模糊综合评价方法,并应用于水质评价方面;2014年延玮辰等[8]在水资源承载力模糊综合评价模型中采用了组合权重法,避免了单一赋权法的不全面性。

基于模糊综合评价法以往的一些改进,本文利用变异系数法与层次分析(analytic hierarchy process,AHP)法相结合来计算组合权重,将灰色关联分析法中的灰关联系数应用于模糊综合评价模型中的模糊关系矩阵,对模糊综合评价模型提出进一步的改进,后将其应用于区域水资源承载力评价中,且将评价结果与传统模糊综合评价法进行对比,分析改进后的模型的可用性。

1 研究方法

1.1 传统模糊综合评价法

传统的模糊综合评价方法是以模糊数学的隶属度理论为基础,对受到多重因素制约的对象做出一个总体评价,并将定性评价转化为定量评价。传统模糊综合评价法的评判步骤如下:

步骤1：选择n个评价因子按照一定的顺序进行排列,形成具有n个元素的评价因素集U={u1,u2,…,un};

步骤2：将水资源承载能力定为m个等级,根据所分的评价等级,建立评价集V={v1,v2,…,vm};

步骤3：计算评价因素集U内各个因素的权重,确定评价指标的权重向量集W={w1,w2,…,wn},确定权重的方法有加权法、AHP法等;

步骤5：将评价因素的权重向量集与模糊关系矩阵通过合适的合成算子进行模糊运算,并且进行归一化,得到模糊综合评价结果。模糊运算采用模糊算子M(·,⨁)(先乘后加)进行计算,可得综合评价值:B=W∘R,B是最后的综合评判矩阵。

1.2 改进的模糊综合评价法

1.2.1 结合主观、客观赋权法确定组合权重

a. AHP法。AHP法确定权重首先要将评估目标分解成一个多级指标,然后判断每一层中各指标的相对重要性。并且引入1～9比率标度对判断出的相对重要性进行定量。AHP法能够综合考虑评价指标体系中各级指标的重要程度,但是在采用分级定量法赋值来构造权重判断矩阵时,会出现系统中不同因素的权重相差巨大的问题,而且该方法主观性较强,无法给出客观的赋值。

b. 变异系数法。变异系数法是一种客观赋权的方法，根据各项指标直观反映的信息,利用公式计算得到指标权重。在评价指标体系中,某一指标取值差异越大,说明该指标实现难度越大,这样的指标更能准确的反映被评价单位的差距。而由于评价体系内各项指标的量纲不同,为了消除量纲的影响,采用各项指标的变异系数来衡量各项指标取值的差异程度。变异系数计算公式为

(1)

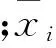
各项指标的权重为

(2)

式中,qi为变异系数法计算出的指标权重。

c. 组合权重。组合权重采用的是集成赋权法,即综合主观、客观赋权法,在保留原有数据的基础上,参考人们对各指标重要程度的给分,结合AHP法和变异系数法计算的各指标权重，从而确定各指标的组合权重，计算公式为

(3)

式中:pi为层次分析法计算出的指标权重;wi为组合权重。

1.2.2 利用灰关联法确定隶属度矩阵

灰关联法是基于灰色系统理论的一种综合分析方法,一般用于定量描述并比较一个系统的发展变化态势。而关联系数则用于反映评价对象与标准对象的接近程度,关联系数越大,评价对象越接近于标准对象。灰关联分析法计算灰关联系数的基本步骤如下:

步骤1：确定参考序列x0(k)和比较序列xi(k)。以评价区域各指标值为参考序列,以评价阶段各指标标准值为比较序列。

步骤2：序列无量纲化。为消除评价指标量纲和单位不同带来的影响,需对序列进行无量纲化处理。

无量纲化方法为

(4)

(5)

表1 江阴市各评价指标数据

式中,Yi(k)、Y0(k)为无量纲后的指标序列。

步骤3：计算绝对差序列。

(6)

式中,Δ0i(k)为绝对差序列。

步骤4：计算关联系数。

本文将灰关联法运用于模糊综合评价中,采用灰关联系数代替传统模糊综合评价法的隶属度,即将xi(k)与x0(k)的关联系数作为其隶属度,即指标xi(k)对评价等级的隶属程度。

2 实例应用

2.1 江阴市概况

江阴市位于119°59′E～120°34′30″E,31°40′34″N～31°57′36″N,地处长江三角洲太湖平原北端,属于典型的平原河网区。其地形主要有长江冲积平原、太湖水网平原和低山丘陵。江阴市属北亚热带季风气候区,又靠近长江下游入海口,受海洋性气候影响,多年平均气温16.7℃,平均降水量1 047.8 mm。

2.2 数据来源

根据《江阴年鉴(2012年)》和《2011年江阴市水资源公报》,选取基准水平年2011年(保证率为75%)的各项评价指标数据,和根据《江阴市水资源综合规划(2011—2030)》得到的2020、2030年江阴市各项指标的预测数据作为研究对象,见表1。

2.3 评价指标体系构建

在综合了江阴市水资源状况、社会经济发展情况、生态环境保护3方面的因素后,构建了多层次递阶结构的水资源承载力评价指标体系。体系分为3个层次。目标层O为水资源承载力;准则层C由水资源系统C1,社会经济系统C2,生态环境系统C33个系统构成;指标层U包括:人均供水量U1,需水模数U2,万元GDP用水量U3,居民生活用水定额U4,工业用水重复率U5,灌溉水有效利用系数U6,年人均GDPU7,生态环境用水率U8。

根据选定的8个评价指标对区域水资源承载力的影响程度,借鉴国内其他学者水资源承载力评价标准[9-10],将其分为3个等级:Ⅰ级(v1)表示该区域水资源承载力较强,水资源可开发利用的潜力大,水资源现阶段不会制约区域的可持续发展;Ⅱ级(v2)表示该区域水资源承载力适中,水资源开发利用已达到一定规模,但仍具有一定的开发利用潜力,水资源有可能成为该区域发展的制约因素;Ⅲ级(v3)表示该区域水资源承载力较弱,水资源进一步开发利用空间有限,水资源状况已明显制约该区域社会经济的发展。指标层分级标准见表2(其中A为综合评分值)。

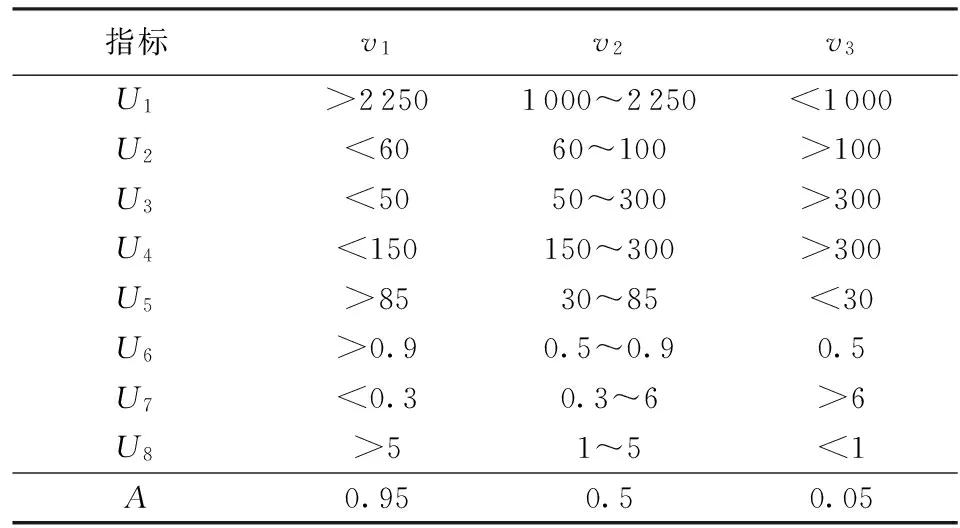
表2 指标层分级标准及评分值

由于等级v1、v2、v3的递减关系,A=0.95v1+0.5v2+0.05v3将评判集等级数量化,等级越高,A的值越大,得分越高,代表水资源承载力也越强。所以,用A来定量地反映各等级水资源承载能力状态:A<0.4时,水资源承载力属于Ⅲ级；0.4≤A<0.7时，属于Ⅱ级；A≥0.7时,属于Ⅰ级。

2.4 各指标权重

根据建立的江阴市水资源承载力评价指标体系,用AHP法计算各指标的权重时,必须对各单层和总层次进行一致性检验,检验结果小于0.1,满足一致性,AHP法计算的指标层各指标权重结果见表3,准则层C1、C2、C3的权重分别为0.311、0.493、0.196。

表3 AHP法计算的指标层权重

根据式(1)～(2)计算变异系数法权重,由式(3)得到组合权重,结果见表4。

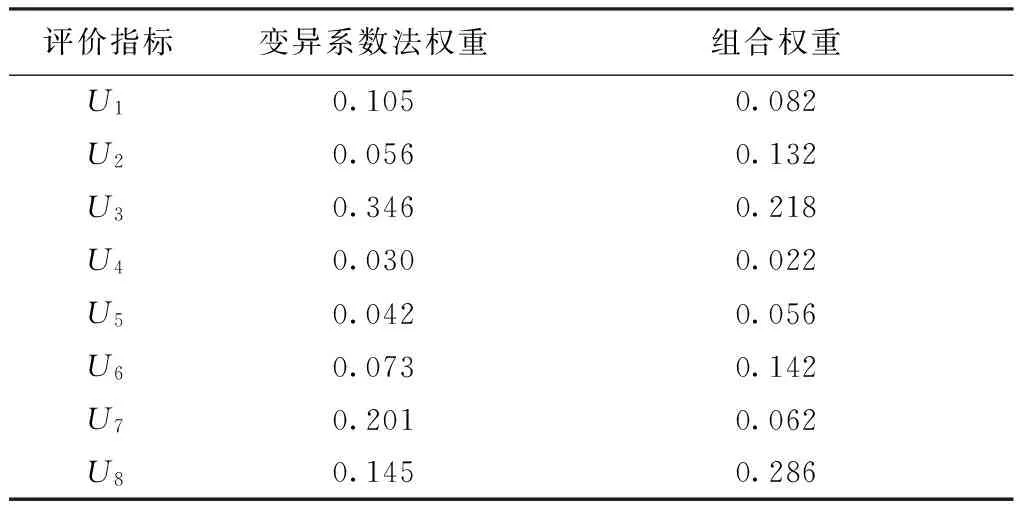
表4 指标层变异系数法权重和组合权重

2.5 关系矩阵

传统模糊综合评价是基于已构建的指标集Ui(i=1, 2, …, 8)和评判集V={v1,v2,v3},采用线性隶属度函数计算得到各等级模糊子集的隶属度,进而确定模糊关系矩阵:

改进模糊综合评价法是用灰关联系数替代隶属度,构建关联系数矩阵。由式(4)～(6)计算得到灰关联系数矩阵如下:

2.6 综合评价结果

分别采用传统模糊综合评价法和改进的模糊综合评价法计算江阴市不同水平年的水资源承载力，最终评判结果矩阵B及综合评分值A的结果见表5。

根据最大隶属度原则以及综合评分值A,对表5的结果进行分析。传统模糊综合评价法对江阴市不同水资源承载力的评价结果是:江阴市水资源承载力在2011、2020和2030年对v2隶属度最大,结合综合评分标准均高于0.4且低于0.7可得,江阴市水资源承载力一直处于Ⅱ级,即表示该区域水资源承载力适中,水资源开发利用仍具有一定的开发利用潜力。改进模糊综合评价法的评价结果为:江阴市不同水平年的水资源承载力对于3个等级的隶属度相差不大,且对于v2的隶属度略大于其他2级,其综合评分值较传统模糊评价法有所提高,但仍处于Ⅱ级状态。

表5 江阴市不同年份水资源承载力综合评价结果

3 结 论

a. 用主观赋权法与客观赋权法相结合计算得到的组合权重代替单一方法确定的权重,可减少主观因素对评价结果的影响;结合灰色关联分析法对模糊综合评价模型进行改进,克服单一方法使用过程的不足,可使评价结果更加全面客观。

b. 改进后的方法应用于江阴市水资源承载力评价,与传统模糊综合评价法相比,综合评价结果相同,但是计算得出的结果对于各个评价等级的隶属度差距减小,降低了主观影响,说明该方法在区域水资源承载力评价中应用良好。

[ 1 ] 贾嵘,薛惠峰.区域水资源承载力研究[J].西安理工大学学报,1998,14(4):382-387.(JIA Rong,XUE Huifeng.Research on the bearing capacity of regional water resources[J].Xi’ an University of Technology,1998,14(4):382-387.(in Chinese))

[ 2 ] 朱一中,夏军,谈戈.西北地区水资源承载力分析预测与评价[J].资源科学,2003,25(4): 43-48.(ZHU Yizhong,XIA Jun,TAN Ge.Measurement and evaluation of water resources carrying capacity of Northwest China[J].Resources Science,2003,25(4): 43-48.(in Chinese))

[ 3 ]卜楠楠,唐德善,尹笋.基于AHP法的浙江省水资源承载力模糊综合评价[J].水电能源科学,2012,30(3): 42-44.(BU Nannan,TANG Deshan,YIN Sun.Fuzzy comprehensiove evaluation of carrying capacity of water resources in Zhejiang Province based on AHP method[J].Water Resources and Power,2012,30(3): 42-44.(in Chinese))

[ 4 ] 付强,王立,宋艳芬.对模糊综合评判决策模型的认识及改进[J].农机化研究,2002(2):27-29.(FU Qiang,WANG Li,SONG Yanfen.The understanding and improvement of fuzzy comprehensive evaluation decision model[J].Agricultural Mechanization Research,2002(2):27-29.(in Chinese))

[ 5 ] 蒋金良,袁金晶,欧阳森.基于改进隶属度函数的电能质量模糊综合评价[J].华南理工大学学报(自然科学版),2012,40(11):107-112.(JIANG Jinliang,YUAN Jinjing,OUYANG Sen.Fuzzy comprehensive evaluation of power quality based on improved membership function[J].South China University of Technology(Natural Science Edition),2012,40(11):107-112.(in Chinese))

[ 6 ] 刘力,周建中,杨俊杰,等.基于信息熵的改进模糊综合评价方法[J].计算机工程,2009,35(18):4-6.(LIU Li,ZHOU Jianzhong,YANG Junjie,et al.Improved fuzzy comprehensive assessment method based on information entropy[J].Computer Engineering,2009,35(18):4-6.(in Chinese))

[ 7 ] 徐健，吴玮，黄天寅，等.改进的模糊综合评价法在同里古镇水质评价中的应用[J].河海大学学报(自然科学版)，2014，42(2)：143-149.(XU Jian,WU Wei,HUANG Tianyin,et al.Application of improved fuzzy comprehensive.evaluation to water quality evaluation in Tongli Town[J].Journal of Hohai University(Natural Sciences),2014，42(2)：143-149.(in Chinese))

[ 8 ] 延玮辰,何俊仕,董克宝,等.基于组合权重方法对蒲河流域水资源承载能力模糊综合评价[J].节水灌溉,2014(7):34-37.(YAN Weichen,HE Junshi,DONG Kebao,et al.Fuzzy comprehensive evaluation of carrying water resources capacity of Puhe River Basin based on combination weighting method[J].Water Saving Irrigation,2014(7):34-37.(in Chinese))

[ 9 ]孙远斌,高怡,石亚东,等.太湖流域水资源承载能力模糊综合评价[J].水资源保护,2011,27(1): 20-23.(SUN Yuanbin,GAO Yi,SHI Yadong,et al.Fuzzy assessment of water resources carrying capacity in Taihu Basin[J].Water Resources Protection,2011,27(1): 20-23.(in Chinese))

[10]任黎,杨金艳,相欣奕.江苏沿海地区水资源承载力研究[J].水利经济,2015,33(5): 1-3.(REN Li,YANG Jinyan,XIANG Xinyi.Water resource carrying capacity in coastal areas of Jiangsu Province[J].Journal of Economics of Water Resources,2015,33(5): 1-3.(in Chinese))

Application of improved fuzzy comprehensive evaluation method to water resources carrying capacity evaluation

YUAN Yanmei1, SHA Xiaojun2, LIU Yuqing1, GAO Yinghui1, LIU Jun1

(1.CollegeofHydrologyandWaterResources,HohaiUniversity,Nanjing210098,China; 2.WaterResourcesManagementOfficeofJiangyin,Jiangyin214400,China)

The coefficient of variation method and the analytic hierarchy process (AHP) method were used to calculate combined weights. The grey correlation coefficient of the grey correlation analysis method was applied to the fuzzy relation matrix in the fuzzy comprehensive evaluation model. Combined with qualitative and quantitative analyses, the fuzzy comprehensive evaluation model was modified. The improved fuzzy comprehensive evaluation method was used to evaluate the water resources carrying capacity of Jiangyin City. The evaluation results agreed with those of the traditional fuzzy comprehensive evaluation method. In addition, the degree of membership with regard to various evaluation grades showed an insignificant difference, and the subjective effect was reduced, indicating that the improved evaluation method is applicable to regional water resources carrying capacity.

fuzzy comprehensive evaluation; combined weights; grey relational analysis; water resources carrying capacity

10.3880/j.issn.1004-6933.2017.01.011

国家自然科学基金(41471015)

袁艳梅(1992—),女,硕士研究生,研究方向为城市防洪排涝与水资源配置。E-mail:18251820730@163.com

刘俊,教授,博士生导师。E-mail:ljhohai@163.com

TV211.1

A

1004-6933(2017)01-0052-05

2016-05-19 编辑：王 芳)