基于拟牛顿法确定参数的时间序列迭代模型

刘永来

摘要： 为解决时间序列参数估计收敛速度慢，迭代次数多，效率低的问题，建立了一种基于拟牛顿法的参数估计方法。实例表明，由此所建立的时间序列迭代模型稳定可靠，拟合、预测精度高，能够有效的表征形变量随时间的变化规律。

Abstract： In order to solve the problem of slow convergence rate， multiple iterations， the low efficiency， a parameter estimation method based on Quasi Newton method is established. The example shows that the time series iteration model established by this method is stable and reliable， and the fitting and prediction accuracy is high， which can effectively characterize the variation of the shape variable with time.

关键词： 拟牛顿法；时间序列；拟合、预测

Key words： Quasi-Newton method；time series；fitting and prediction

中图分类号：O241.7 文献标识码：A 文章编号：1006-4311（2017）02-0183-02

0 引言

时间序列模型是将形变量按时间的先后顺序进行排列，不考虑外界因素对后期预测的影响，且模型理论简单，建模过程简便，能够有效的表征形变量随时间的变化规律[1，2]。在时间序列建模过程中，模型参数估计是非常重要的工作，参数估计可以描述为对时间序列目标函数式的无约束优化问题，可通过工程优化方法求解其极值将参数求出。通常无约束优化问题的求解可分为导数解法和直接解法两大类。由于直接解法较导数解法的算法要慢，通常使用导数解法。导数解法可分为最速下降法[3]、牛顿法[4]、共扼梯度法[5]和拟牛顿法[6]。当四种方法对时间序列的进行参数估计时，最速下降法和共扼梯度法建模过程复杂，模型收敛速度较慢，牛顿法的收敛速度很快，但是得保证Hesse矩阵可逆，拟牛顿法（DFP）不需要对Hesse矩阵求逆，而且迭代次数少[6，7]，效率高，计算过程简单有效。本文基于拟牛顿算法求解时间序列模型参数，以建立时间序列迭代模型，并以实例加以验证，以确保模型的有效性。

1 时间序列模型

1.1 时间序列模型的建立

3 实例分析

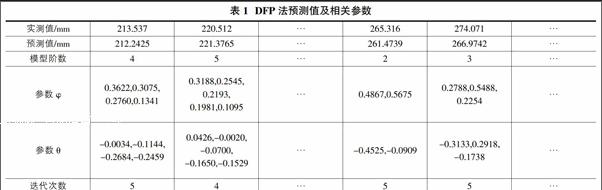
以文献[9]中某监测点2005年4月到2008年7月共40期的监测数据为例，用本文所提方法（拟牛顿法确定参数的时间序列迭代模型）进行一步滚动拟合预测[10，11]，部分预测结果、参数、迭代次数见表1。

将预测精度、残差情况与文献[9]中所采用其他方法（ARMA、灰色模型、多项式）进行对比，其结果见表2。

由表1和表2可知，拟牛顿法确定参数的时间序列迭代模型迭代次数较少，迭代次数基本保持在5次左右，大大提高了计算效率，模型拟合、预测误差较小。与ARMA、灰色模型和多项式三种方法相比较，该模型平均残差最小，为25.00mm，而且预测精度最高，达到96.09%；多项式预测精度最低，只有90.34%。因此，拟牛顿法确定参数的时间序列迭代模型建模可靠，预测精度高，有效的反映了形变量随时间的变化规律。

4 结论

基于拟牛顿法的参数估计计算过程简单有效，不需要对Hesse矩阵进行求逆，而且迭代次数少，效率高。由此求得的φ和θ所建立的时间序列迭代模型稳定可靠，拟合、预测精度高，能够有效的表征形变量随时间的变化规律。

参考文献：

[1]黄声享，尹晖，蒋征.变形监测数据处理[M].二版.武汉：武汉大学出版社，2010.

[2]杨建文.变形预测组合模型建模方法研究与精度分析[D].昆明：昆明理工大学，2014.

[3]石琴琴，霍宏，方涛.使用最速下降算法提高极大似然估计算法的节点定位精度[J].计算机应用研究，2008，25（7）：2038-2040.

[4]周西峰，朱文文，郭前岗.基于遗传算法和高斯牛顿法的超声回波信号参数估计[J].解放军理工大学学报（自然科学版），2012，13（3）：247-251.

[5]伍杰.求解对称非线性方程组的共轭梯度法[D].湖南：湖南大学，2010.

[6]袁亚湘.非线性优化计算方法[M].北京：科学出版社，2008.

[7]刘璐，刘洪，张衡，等.基于修正拟牛顿公式的全波形反演[J].地球物理学报，2013，56（7）：2447-2451.

[8]吕忠伟，秦建国.多变量时间序列模型识别方法[J].统计与决策，2007（2）：129-131.

[9]孙世国，杨宏.典型排土场边坡稳定性控制技术[M].北京：冶金工业出版社，2011.

[10]杨建文，杨德宏，汪奇生.基于Helmert方差分量估计建立沉降分析变权组合模型[J].工程勘察，2014，42（10）：73-77.

[11]谢世成，黄定川，张逸仙.顾及点位关联的变形体空间多点预测模型效果分析[J].勘察科学技术，2016（3）：28-31.