链环浮力及型号对锚链形状的影响
2017-02-06张兴国
张兴国


摘要: 针对利用线性模型忽略浮力解决系泊系统中锚链形状参数时所造成误差大的问题,提出考虑浮力的迭代模型。利用该模型,首先计算得到的锚链形状,其与真实情况相比所得结果基本相同;然后研究改变锚链链环型号对锚链形状的影响;最后,在以往的线性模型的基础上做出改进,得到锚链模型。通过对几个模型的比较可以发现,迭代模型和改进后锚链模型均与真实锚链形状相符,没有改进的模型与其有较大的差异。
Abstract: For the large errors caused by the problems of the cable shape parameters of the mooring system solved by the linear model, the buoyancy iteration model is put forward. By using the model, the cable shape is firstly calculated. Its results are basically same with the real situation. Then the effect of the changes of chain link type on the cable shape is studied. Finally, based on the previous linear model, the anchor chain model is obtained. By comparing with several models, it can be found that the iterative model and the modified anchor chain model are consistent with the real chain shape, and there is no significant difference between the improved one and the improved one.
关键词: 迭代模型;锚链形状;锚链浮力
Key words: iterative model;cable shape;cable buoyancy
中图分类号:O59 文献标识码:A 文章编号:1006-4311(2017)02-0143-04
0 引言
随着海上资源开发的增加,系泊系统的运用也越来越广[1]。在系泊系统的设计中即需要考虑水的深度、密度和流速,也要考虑风速、周围环境及障碍物等的影响[2]。目前针对相关研究的文献有很多,但其中大部分文献没有考虑到锚链受到的浮力,且将锚链简化为一根曲线进行计算[3-7],忽略了链环自身不可弯曲的特点[8-10];这样虽然给计算和建模带来了很大方便,但误差也相对较大。相关研究主要采用的方法有微元法[2],微分方程法,回归法[3]和多项式法[4]等,但涉及迭代算法的较少。
本文以系泊系统的锚链为研究对象,建立迭代模型,对考虑锚链受到重力和浮力以及只受到重力时锚链的形状的进行比较;以及其他条件不变的情况下采用不同型号的链环,对锚链的形状变化进行比较。
1 模型的建立
1.1 迭代模型的建立
系泊系统主要组成部分为:浮标、钢管、钢桶、重物球、锚链、锚,见图1。图1中S表示锚链在水平方向上的投影长度,H表示锚链在Y轴方向上投影的高度,β为锚链上端与钢桶连接处的切线与X轴的夹角。大部分有关系泊系统的研究中均考虑了浮标、钢管、钢桶和重物球受到的重力和浮力,但没有考虑锚链的浮力。另外,在大部分文献中,锚链几乎都被简化为一条曲线进行计算,忽略了链环自身不可弯曲的特点。故我们针对上述缺点,对锚链进行研究。
2 模型的求解
2.1 相关参数的设定
以系泊系统在海上为例,假设浮标在水平方向受到风的推动力为898.63N,锚链的总长为22.05m,海水的密度为1.025×103kg/m3,链环的密度为7.85×103kg/m3,重力加速度为9.8m/s2,链环的相关参数及计算获得的参数见表1。
2.2 迭代模型的求解
2.2.1 浮力对锚链形状的影响
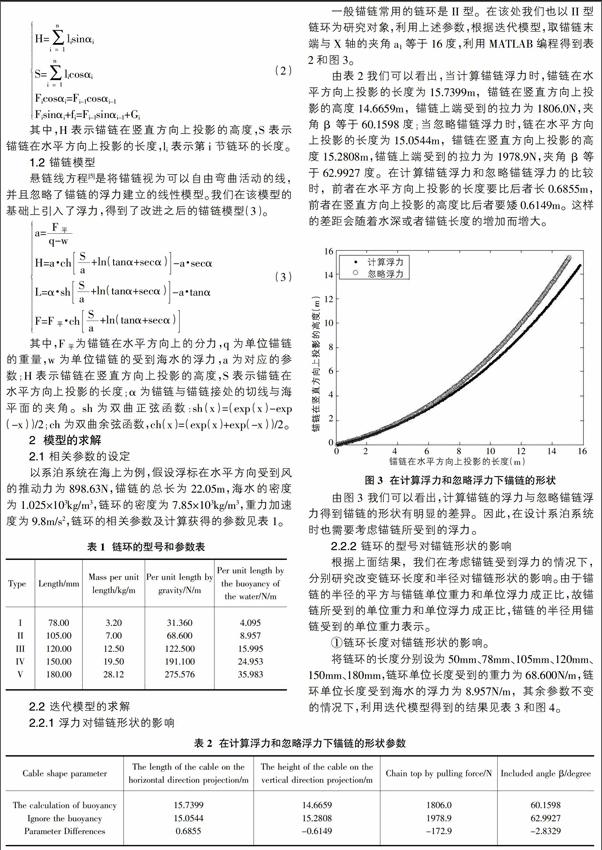
一般锚链常用的链环是II型。在该处我们也以II型链环为研究对象,利用上述参数,根据迭代模型,取锚链末端与X轴的夹角a1等于16度,利用MATLAB编程得到表2和图3。
由表2我们可以看出,当计算锚链浮力时,锚链在水平方向上投影的长度为15.7399m,锚链在竖直方向上投影的高度14.6659m,锚链上端受到的拉力为1806.0N,夹角 β 等于60.1598度;当忽略锚链浮力时,链在水平方向上投影的长度为15.0544m,锚链在竖直方向上投影的高度15.2808m,锚链上端受到的拉力为1978.9N,夹角 β 等于62.9927度。在计算锚链浮力和忽略锚链浮力的比较时,前者在水平方向上投影的长度要比后者长0.6855m,前者在竖直方向上投影的高度比后者要矮0.6149m。这样的差距会随着水深或者锚链长度的增加而增大。
由图3 我们可以看出,计算锚链的浮力与忽略锚链浮力得到锚链的形状有明显的差异。因此,在设计系泊系统时也需要考虑锚链所受到的浮力。
2.2.2 链环的型号对锚链形状的影响
根据上面结果,我们在考虑锚链受到浮力的情况下,分别研究改变链环长度和半径对锚链形状的影响。由于锚链的半径的平方与锚链单位重力和单位浮力成正比,故锚链所受到的单位重力和单位浮力成正比,锚链的半径用锚链受到的单位重力表示。
①链环长度对锚链形状的影响。
将链环的长度分别设为50mm、78mm、105mm、120mm、150mm、180mm,链环单位长度受到的重力为68.600N/m,链环单位长度受到海水的浮力为8.957N/m,其余参数不变的情况下,利用迭代模型得到的结果见表3和图4。
由表3 我们可以看出,锚链在水平方向上投影的长度随链环长度的增加而增加,锚链在竖直方向上投影的高度随链环长度的增加而变矮,但变化趋势不明显。锚链上端受到的拉力和夹角 β 随链环长度的增加而有一定的波动,但波动不明显。
由图4可以看出,在链环长度不断变化时,锚链的形状基本没有变化。因此,锚链链环长度对锚链的形状影响较小。
②链环单位长度的质量对锚链形状的影响。
将链环单位长度的质量分别设为3.20kg/m、7.00kg/m、12.50kg/m、19.50kg/m、28.12kg/m,链环长度为,其余参数不变的情况下105mm,利用迭代模型得到的结果见表4和图5。
由表4 我们可以看出,随着链环单位质量的增加,锚链在水平方向上投影的长度随着变短,锚链在竖直方向上投影的高度随着增加,锚链上端受到的拉力随着增加,夹角 β 也随着增加,且增加均较为明显。
由图5 可以看出,随着链环单位质量的提高,锚链的倾斜角度变化得越快,锚链在水平方向上投影的长度越来越短,链在竖直方向上投影的高度越来越高。链环的单位质量对锚链的形状影响较大,故链环半径对锚链的形状影响较大。
2.3 锚链模型的求解与比较
当F平为锚链在水平方向上的分力为898.6133N,锚链单位长度受到的重力为68.6N/m,单位长度受到的浮力为8.957N/m。利用MATLAB编程分别绘制出我们建立的迭代模型求解得到的锚链形状图,真实的锚链形状图,改进后的线性模型求解得到的锚链形状图和未改进的线性模型求解得到的锚链形状图,具体见图6。
由图6可以看出,我们建立的迭代模型和改进线性模型求解得到的锚链形状与真实的锚链形状基本相似。没有改进的模型与真实的锚链形状相差很远。
3 总结
通过上述的结果比较,我们可以得到:在系泊系统的设计和制作过程中,锚链所受到的浮力是不可以忽略的,忽略之后对结果的影响特别大;链环长度的改变对锚链形状几乎没有影响,可能是由于链环的长度与锚链的长度相比实在不值一提;锚链的单位长度对锚链的形状有较大的影响。我们建立的迭代模型与改进后的线性模型得到的锚链形状均与真实的锚链形状相似,然而没有改进后的线性模型得到的锚链形状与真实的锚链形状有较大的差距。
通过比较分析我们可确定我们建立的迭代模型的优点为:考虑浮力建立的迭代模型具有较高准确性,与真实情况更加相符。另外,迭代模型可以解决锚链末端拖地的情况,线性模型却做不到。
参考文献:
[1]郝春玲,滕斌.不均匀可拉伸单锚链系统的静力分析[J].中国海洋平台,2003(04):19-22,34.
[2]王丹,刘家新.一般状态下悬链线方程的应用[J].船海工程,2007(03):26-28.
[3]侯建军,东昉,石爱国,尹建川.锚泊状态下锚链作用力的计算方法[J].大连海事大学学报,2005(04):12-16.
[4]滕斌,郝春玲,韩凌.Chebyshev多项式在锚链分析中的应用[J].中国工程科学,2005(01):21-26.
[5]胡晓芳,丁德勇.锚链直径对船舶锚泊能力的影响[J].中国舰船研究,2014(04):109-112,119.
[6]胡灵斌,唐军.悬链线方程的求解及其应用[J].船舶,2004(01):17-20.
[7]张光发,纪卓尚,李铁骊,林焰.导管架下水系统驳船锚链力的动态计算[J].中国造船,2008(03):13-19.
[8]肖越,王言英.浮体锚泊系统计算分析[J].大连理工大学学报,2005(05):682-686.
[9]郑瑞杰,刘庆茶.附加悬块锚链结构的受力分析[J].水运工程,2005(11):20-22.
[10]钟于祥.锚泊船舶出链长度及张力估算[J].淮阴工学院学报,2004(03):3-5.
[11]中国船级社.海洋工程锚链规范[M].北京:人民交通出版社,1995.
[12]郝春玲,张亦飞,滕斌,徐伟,赵海涛.流速分布及锚链自身刚度对弹性单锚链系统变形和受力的影响[J].海洋学研究,2006(03):90-95.
