双车道公路平曲线处车辆侧向位置预测方法研究

王玥珩

(中国路桥工程有限责任公司，北京 100011)

0 前 言

双车道公路是我国公路中最为普遍的一种公路类型，作为国家和省内的一般干线公路，在综合交通运输系统中发挥着重要作用。同时，双车道公路的交通安全形势也十分严峻。统计数据表明，我国双车道公路交通事故占全国道路交通事故总数的30%以上。由于具有线形条件特殊和驾驶行为相对复杂的特殊性，公路平曲线已成为交通事故的频发地段。

鉴于公路平曲线具有较高的交通安全风险，国内外学者对此展开了大量研究工作。目前，相关研究成果大多集中在两个方面：(1)车辆在公路平区线处的运行特征；2)公路平曲线的几何设计要求。针对公路平曲线处车辆的运行特征，以往研究重点考虑车辆运行速度特点，研究成果涉及公路平曲线处车辆运行速度特征及预测模型、动态限速与预警方案、建议限速标志设置等。针对公路平曲线的几何设计，主要研究平曲线半径与车辆运行速度和驾驶员生心里反应的相互影响，公路平曲线几何要素与安全视距及交通安全的关系，以及公路平曲线半径的设置规则等。

实际上，除速度用于表征车辆纵向运行状态外，表征其横向运行状态的指标通常为车辆在车道上的运行轨迹，常用车辆侧向位置表征(lateral placement, LP)。统计表明，发生在公路平曲线处的交通事故很大程度由车辆冲出车道或驶向对象车道引起。目前，针对公路平曲线处车辆侧向位置的研究主要集中在影响特征分析层面，基于弯道属性及车辆速度的定量预测模型相对缺乏。因此，本研究重点以车辆在双车道公路平曲线处侧向位置为研究对象，旨在构建双车道公路平曲线处的车辆侧向位置预测模型，为提前感知车辆在弯道处的安全风险提供方法支持。

1 实验设计与数据获取

为构建车辆侧向位置预测模型，需获取不同公路平曲线条件下的车辆运行数据。考虑到实际条件下数据获取较为困难，本研究采用驾驶模拟实验获取基础数据。驾驶模拟实验具有条件可控制、可重复和零安全风险等优势。

1.1 被试选取

共选取30名驾驶员参加驾驶模拟器实验。被试由出租车司机、社会私家车主和在校学生构成，平均年龄32岁，平均驾龄3.5年。

1.2 实验场景设计

模拟驾驶实验场景为双车道公路，每条车道宽度3.5m，直线路段和弯道分别用黄色虚线和实线分离。由于车辆在公路平曲线处行驶时，其运行状态主要受到弯道半径(R)和弯道转向(D)两个因素影响。因此，实验共设计15种公路平曲线，其中曲线半径包括小、中、大三种(R=60,125,150,200,300,400,600,1 000 m)，曲线转向按车辆行驶方向分为左转(D=1)和右转(D=0)两类。实验场景中各平曲线属性如表1所示。

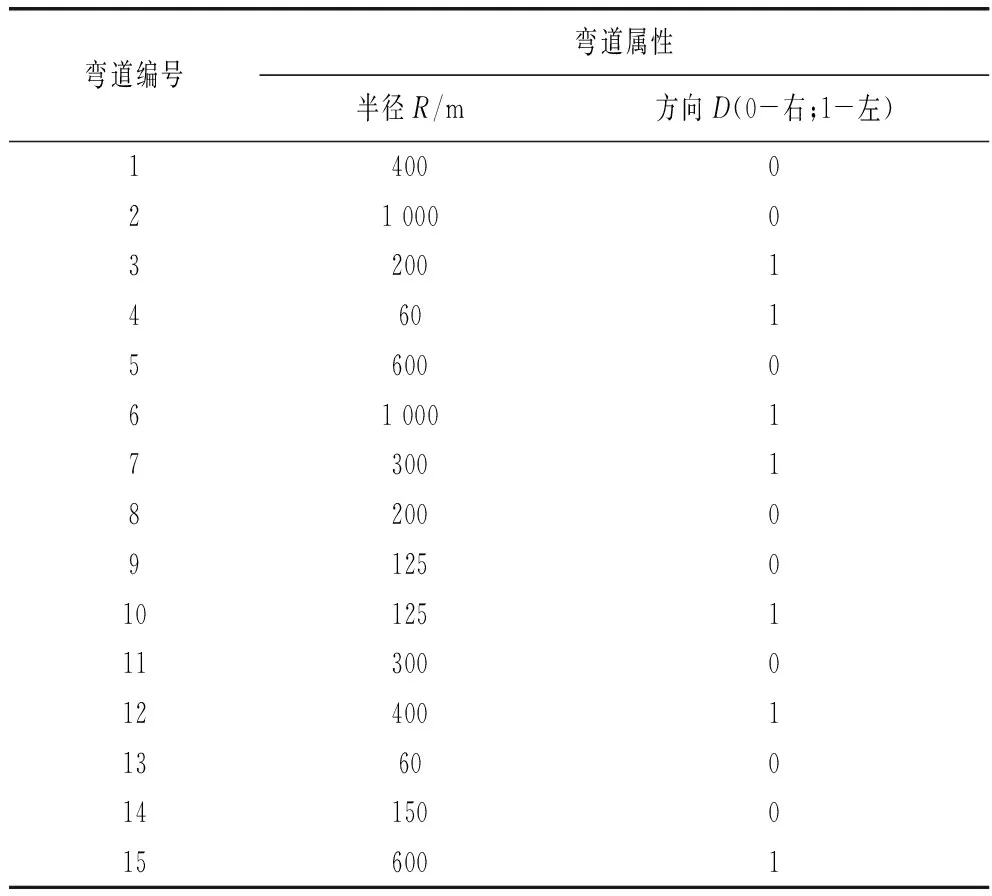
表1 公路平曲线属性统计表

根据我国公路路线设计规范，本研究中，平曲线长度按车辆设计速度行驶5 s以上决定。为避免平曲线间距过近造成车辆行驶状态相互干扰，相邻两平曲线间增设500～800 m直线路段。同时，考虑到第一和最后一个弯道的实验数据易受到驾驶员主观影响，在场景开始和结束位置分别设置1 km直线路段以确保客观真实反映驾驶员的驾驶行为状态。因此，实验场景总长度为13.5 km。整个实验过程中，不增设实验车以外的其它车辆，以最大程度降低外界影响因素对实验数据的干扰。实验时间环境设置为白天。

1.3 实验流程安排

(1)驾驶练习。考虑到驾驶员首次驾驶模拟器时需要一定的适应和学习过程，为避免不熟悉驾驶模拟器操作而影响实验数据，每名被试须进行3～5 min的驾驶练习。驾驶练习场景为与正式实验场景相似的双车道公路，包括不同半径和转向的双车道公路平曲线。

(2)驾前问卷。被试在完成驾驶练习进行正式实验前，需填写主观问卷。问卷内容一方面包括驾驶员的年龄、职业、驾龄等基础信息；另一方面，通过主观问卷获取驾驶员的疲劳程度及身体状态，确保驾驶员未受到药物、酒精及刺激性食物的影响，最大限度地获取正常状态下的实验数据。

(3)正式实验。依据各自不同的行车速度，完成正式实验场景测试耗时10～15 min。实验过程中，要求驾驶员按照交通法规行驶，并根据道路条件调整车辆行驶状态。

2 数据采集与预测模型构建

2.1 数据采集

由于发生在公路弯道处的交通事故，很大比例由车辆冲出车道或驶入对象车道而引发。因此，本研究选用车辆在曲线处的侧向位置(lateral placement, LP)作为分析指标。当车辆位于右侧车道中心位置行驶时，LP值为0；随着车辆偏离车道中心越远，LP取值越大。

由于驾驶员视线和弯道线形变化等因素的相互作用，车道在弯道中点发生事故的概率较大，本研究选取弯道中点处的LP值为预测指标，如图1所示。另外，除弯道本身属性(半径和转向)的影响，车辆LP与车辆速度存在较大关联；同时考虑到实际应用中，车辆降速理应在进入弯道前完成，因此研究选取弯前控制点处(见图1)的速度值作为LP的解释变量。

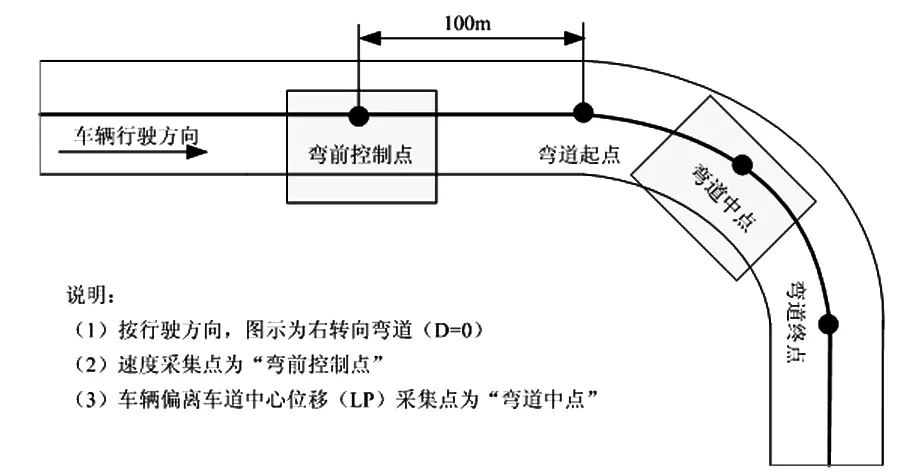
图1 数据采集点说明

2.2 数据处理与分析

实验包含30名被试，每名被试驾驶完成15种公路平曲线，共采集获得450个实验样本数据。将30名被试随机分成6组，每组5名，前5组被试数据用于构建预测模型，最后1组被试数据用于验证模型预测精度。因此，共有375个样本数据用于模型构建，75个样本数据用于模型验证。

考虑到模拟器记录实验数据时可能存在跳过关键点的情况，为准确反应车辆在特定点的状态，本研究利用场景坐标，选取数据采集点前后各1m内的数据均值代表车辆在该点处的运行特征。出于数据展示说明，统计用于模型构建的25名被试在不同弯道场景下的入弯前速度和弯道中心处车辆侧向位置的均值和标准差如表2所示。

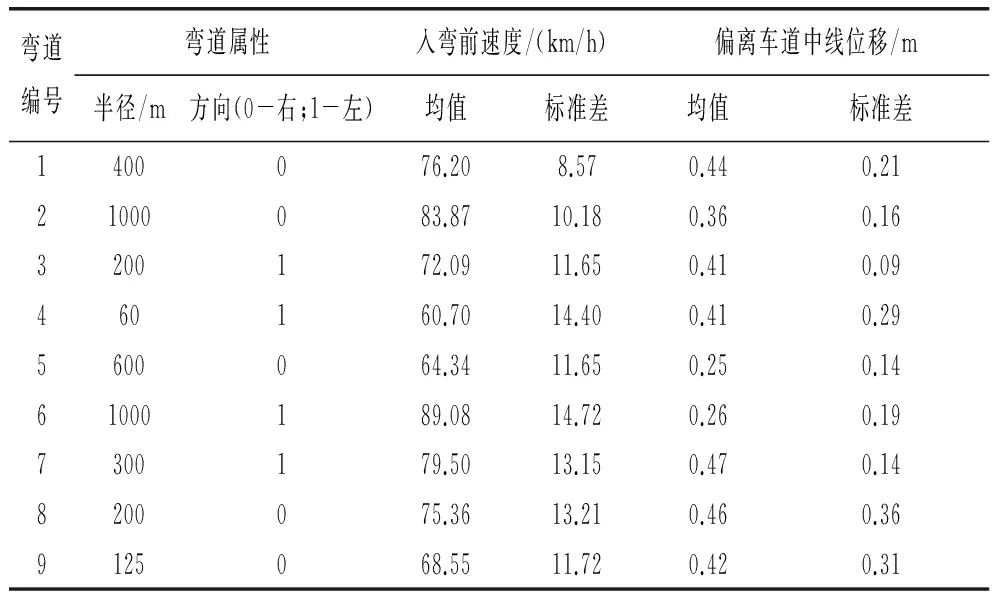
表2 建模数据描述性统计

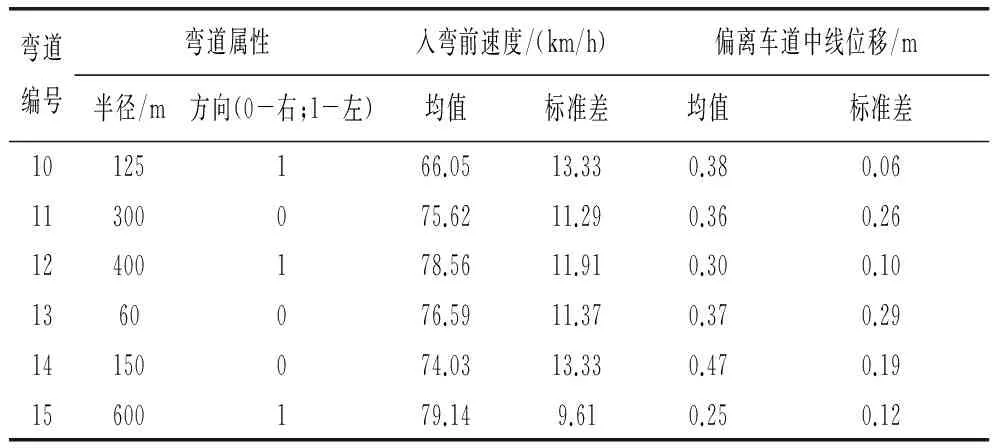
续表2

2.3 模型假设

研究通过构建线性回归模型实现车辆在双车道公路平曲线处行驶时的侧向位置预测。其中，因变量为车辆侧向位置LP，自变量为弯前控制点车速(见图1)以及弯道半径(R)和弯道转向(D)。考虑到弯道方向为0-1变量(0-右弯；1-左弯)，因此构建模型形式如下：

LP=α0+α1SP+α2R+α3D+α4R*D+α5SP*D+ε

(1)

式中：LP为车辆侧向位置，m；αi为回归系数，i=0,1,2,…,5；SP为弯前控制点车速，距离弯道起点100 m，km/h；R为弯道半径，m；D为弯道转向，左弯时D=1，右弯时D=0；ε为随机误差项。

2.4 模型构建

考虑到车辆运行状态在不同驾驶个体之间可能存在差异，研究通过R语言分别构建固定效用和随机效用两种线性回归模型，并通过Hausman检验确定最终模型。当Hausman检验结果的p值小于0.05时，选用固定效用模型；反之选用随机效用模型。

基于前5组25名被试的375个样本数据进行回归拟合，Hausman检验结果为p=1.0，因此应选用随机效用回归模型。采用逐步回归方法，结果显示：模型拟合度(R2)为0.68，回归方程显著性检验为F(4,370)=21.803;p<0.001，回归模型系数及检验结果如下表3所示。

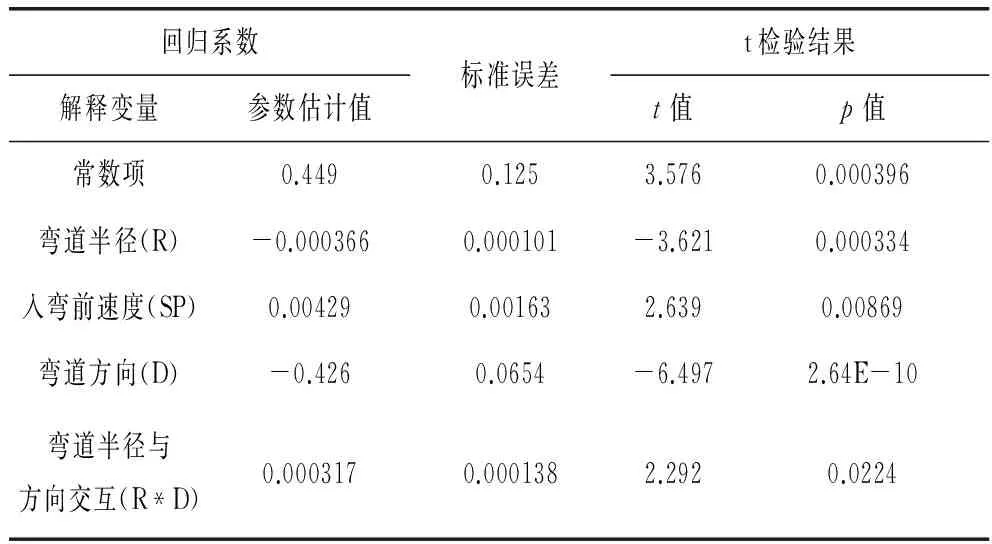
表3 回归模型系数及检验结果

由表3可获得车辆侧向位置的预测模型如下：

LP=0.44+-0.000 37R+0.004 3SP-0.426D+0.003 2R*D

(2)

3 模型验证

利用第6组5名被试的75个样本数据进行模型验证，统计车辆在不同平曲线条件下侧向位置的平均实际值和预测值如下表4所示。通过预测值与实际值的绝对差值和实际值之比，得到模型的预测误差。最大误差为16.85%，最小误差为0.40%，平均误差为5.68%。由此可知，预测模型具有较高的精度，平均预测精度为94.32%。

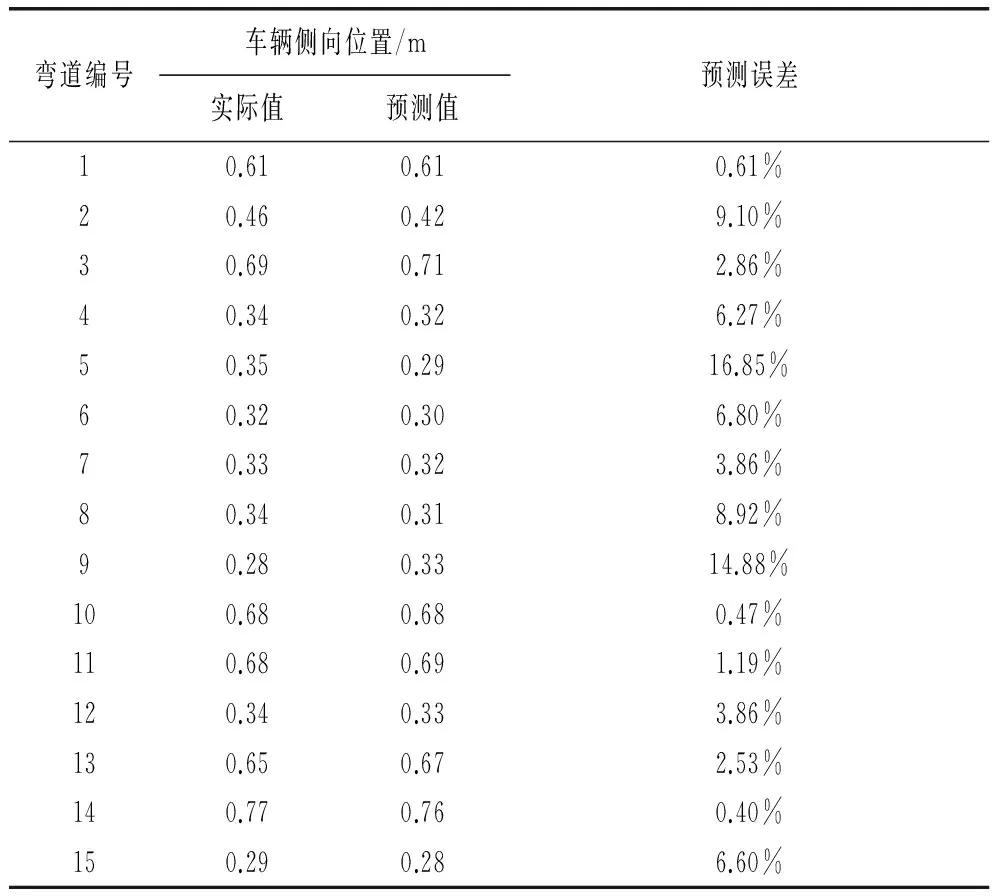
表4 模型预测结果验证

4 结 论

基于驾驶模拟器实验，获取车辆在不同双车道公路平曲线处的行驶状态。以车辆在弯道中点处侧向位置为因变量，车辆在进入弯道前的速度和弯道半径及转向为自变量，构建了基于随机效用的线性回归模型，实现了车辆侧向位置的准确预测，平均预测精度为94.32%。研究结果方便提前感知车辆在弯道处的安全风险，有助于预防和减少弯道处车辆冲出车道或驶向对向车道而引发的交通事故。

目前研究基于驾驶模拟实验展开，未能反应车辆在弯道处行驶时离心率、超高等因素的影响，不能完全反应实际行车状况，下步重点需通过外场实测数据对模型的有效性实施进一步验证。

[1] 交通部公路科学研究院. 2014年中国道路交通安全蓝皮书[M]. 北京:人民交通出版社, 2015.

[2] 丁传鑫. 双车道公路平曲线对车辆行驶轨迹的影响研究[D].安徽: 安徽理工大学, 2014.

[3] 宋涛, 张永生, 郭彩香. 山区公路平曲线运行速度预测模型研究[J].交通运输工程与信息学报, 2007, 15(1): 118-123.