铸态50Cr5MoV钢的动态再结晶行为分析

王耀琨 杜 佳 陈 阳 李钊库

(中冶陕压重工设备有限公司，陕西711711)

铸态50Cr5MoV钢的动态再结晶行为分析

王耀琨 杜 佳 陈 阳 李钊库

(中冶陕压重工设备有限公司，陕西711711)

采用Gleeble-3800热模拟实验机对铸态50Cr5MoV钢进行热压缩实验，研究其在变形温度为900℃、950℃、1 000℃、1 050℃、1 100℃和应变速率为0.01 s-1、0.1 s-1、1 s-1条件下的动态再结晶行为。结果表明：铸态50Cr5MoV钢在热变形过程中发生了动态再结晶，且随着应变速率的降低以及变形温度的升高，动态再结晶越容易发生。

铸态50Cr5MoV钢；动态再结晶；本构方程；临界应变模型

轧辊是轧机的重要设备，由于轧机特殊的工作环境，要求轧辊必须具有良好的耐磨性、高屈服强度和抗剥落性能，辊颈具备高强韧性和抗断裂性能。50Cr5MoV钢是继第一代2%Cr材质、第二代3%Cr材质之后研发出的第三代锻辊用钢，其淬透性、疲劳强度以及抗事故性能均比第一代、第二代材质有明显提高，已逐渐成为现代化板带轧机轧辊的主要用钢，并将在较长一段时间内占据主导地位[1-2]。

动态再结晶是金属热加工生产过程中控制组织与性能的有效手段之一[3-4]。动态再结晶使得50Cr5MoV钢在热锻成型过程中的微观组织发生转变，通过调节热锻工艺，可以细化奥氏体组织，优化材料的力学性能，从而提高50Cr5MoV轧辊的使用寿命。本文利用Gleeble-3800热模拟机对铸态50Cr5MoV轧辊钢进行高温压缩试验，研究其动态再结晶行为，并建立了动态再结晶模型，为制定合理的锻造工艺提供理论依据，从而优化锻钢轧辊的综合性能。

1 实验材料及方法

本实验所用设备为Gleeble-3800热力模拟实验机，实验材料为50Cr5MoV轧辊钢(铸锭)，其化学成分如表1。

表1 50Cr5MoV轧辊钢的化学成分(质量分数，%)Table 1 Chemical compositions of 50Cr5MoV roll steel (mass fraction, %)

从铸锭上截取样品，制成∅10 mm×15 mm的圆柱型试样，在Gleeble-3800型热模拟机上进行压缩实验。以10℃/s速度将试样加热至1 150℃以便奥氏体化，进行3 min保温，然后将试样以10℃/s的冷速分别冷却至900℃、950℃、1 000℃、1 050℃和1 100℃，为了消除试样内部的温度差，样品保温20 s，进行压缩变形，变形量按70%控制，变形速率分别按照0.01 s-1、0.1 s-1和1 s-1进行控制。实验过程中记录应力-应变数据，变形后的样品立即淬火，将奥氏体组织固定到室温。实验过程如图1所示。

2 实验结果与分析

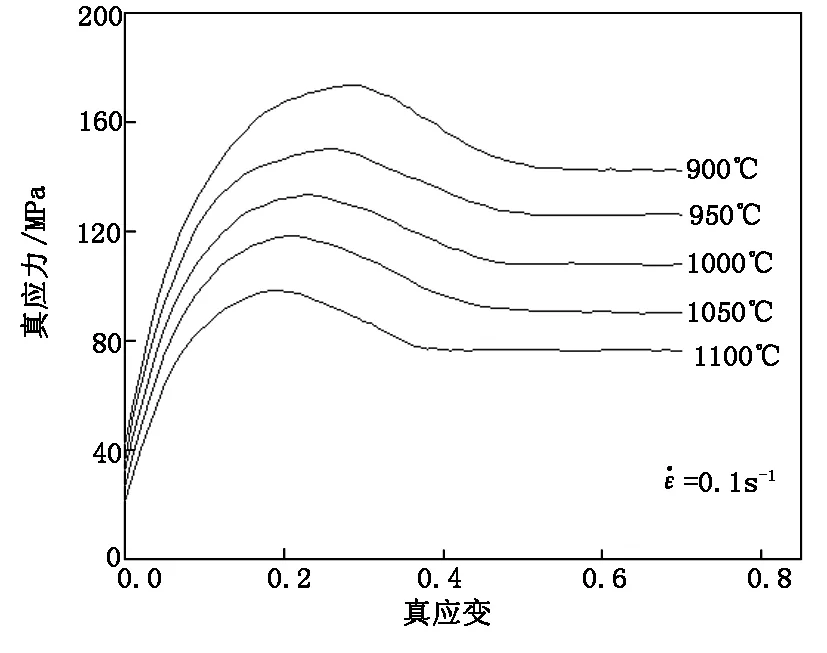
通过压缩变形过程所记录的数据，采用Origin绘图软件对数据进行处理，可以得到50Cr5MoV轧辊钢在不同实验条件下的真应力-真应变曲线，如图2所示。

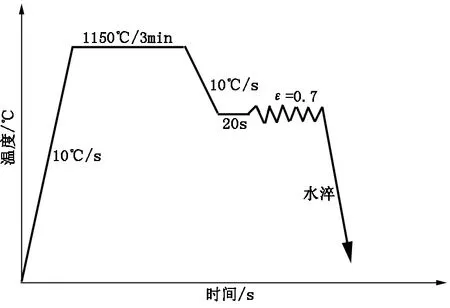
图1 实验钢热模拟实验工艺Figure 1 The thermal simulation process of tested steel

(a)

(b)

(c)图2 50Cr5MoV轧辊钢的真应力-应变曲线Figure 2 The true stress-strain curve of 50Cr5MoV roll steel

由图2可知，50Cr5MoV钢流变应力受温度及应变速率的影响显著。在变形开始阶段，随着形变量的不断增加，流变应力以较快的速度增大。分析认为，在变形开始阶段，形变量增加，位错发生了滑移等运动，位错运动引起的软化作用不足以抵消位错密度增加所导致的硬化作用，因此，流变应力迅速增加，形变强化作用显著[5]。后续变形的曲线呈现两种不同的主导软化态势，即动态再结晶(DRX)和动态回复(DRV)。

在0.01 s-1～0.1 s-1的低应变速率条件下，如图2(b)所示，流变曲线具有明显的应力峰值，说明压缩变形过程中发生了动态再结晶，随着动态再结晶程度的不断增大直至发生完全动态再结晶，位错增值所引起的加工硬化与位错运动、位错脱钉等引起的动态软化达到动态平衡，变形进入了稳态流动阶段[5]。

在1 s-1的较高的应变速率条件下，如图2(c)中温度为900℃的曲线，应力到达一定程度后，随着应变量的增加，流变应力趋于平稳，为动态回复型软化。这是因为加工硬化率不是随着变形程度的增加而一直增大，在材料发生加工硬化的同时，变形产生的位错能够通过交滑移和攀移等方式运动，使部分位错消失，部分位错重排，从而造成金属材料的回复软化。这种情况下，整个软化过程由动态回复控制[6]。

当应变速率一定时，动态再结晶行为随着变形温度的升高越明显，而最大流变应力相应降低。因为变形温度升高增强了变形的热激活作用，晶界可动性也增强，有利于动态再结晶形核和晶粒长大以及位错湮灭，这将会降低流变应力[7]。当变形温度一定时，再结晶晶粒形核和长大时间随着应变速率的降低变得更为充分，动态再结晶进行得越充分。同样位错之间的交互作用导致位错密度急剧增加，增加了变形储存能，从而引起再结晶的临界温度的降低，动态再结晶程度也相应增加。

3 动态再结晶动力学模型

3.1 热变形本构关系模型

研究表明，金属材料的高温流变应力既与成分有关，又与形变温度和应变速率有关，在材料的成分不变时，采用Arrhenius双曲正弦函数描述50Cr5MoV钢的本构关系[8]：

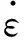
C.M.Sellars和W.J.M.Tegart提出并实验验证了热变形条件，通常可以用温度补偿的应变速率因子Zener-Hollomon参数Z来表示，Z参数可用下式表示[9]：

根据应力条件高低的不同，式(1)可以简化为以下两种方式：

其中，系数α、β及n1之间满足α=β/n1。

因此，可以通过式(3)和式(4)确定α值。根据文献的求解方法[10]，可得α=0.007 7。

当对式(1)进行Tayler级数展开时发现，在低应力条件下较为接近式(3)，在高应力条件下接近式(4)，因而采用式(1)基本能适用于描述整个应力范围的热变形过程，且众多研究结果[11-12]表明，式(1)能够较好地描述金属材料的常规热变形过程。

对式(1)进行变换处理可得：

对式(5)两边取对数并求偏微分，可得热变形激活能Qdef的表达式：

经过计算，可得50Cr5MoV钢热变形激活能Qdef=333.47kJ/mol，b=5 689.33，n=7.05。因此，50Cr5MoV钢的动态再结晶数学模型为：

(7)

热变形过程中，通过对lnZ和ln[sinh(ασp)]进行线性拟合(见图4)，可求得lnA=28.11。结合图4、式(7)，50Cr5MoV钢的高温热变形本构方程可表示为：

(8)

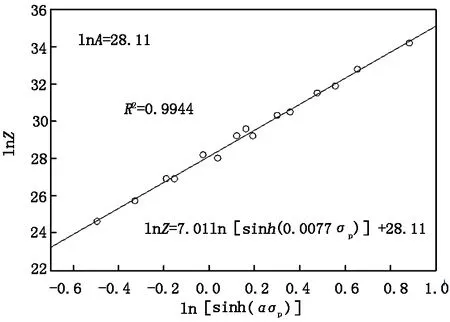
图4 ln[sinh(ασp)]与lnZ的关系图Figure 4 The relationship between ln[sinh(ασp)] and lnZ

3.2 动态再结晶临界应变模型

动态再结晶是否发生，通常用临界应变量(εc)来判断，只有形变量大于εc时，才会发生动态再结晶[13]。因此，准确地确定临界应变量εc，对研究热变形工艺参数尤为重要。在以往的科研工作中，研究人员提出了许多数学模型用于预测动态再结晶开始的临界条件[5,14]。Poliak和Jone等人提出了计算动态再结晶临界应变的方法，可由下式表示：

式中，θ表示加工硬化率，θ=dσ/dε。

动态再结晶发生时的临界应变点由(-dθ/dε)-ε关系曲线确定。而Najafizadeh-Jonas对以上方法做了简化，通过lnθ-ε曲线分析法确定临界应变。在本研究工作中，采用类似Najafizadeh-Jonas的方法，通过对lnθ-ε曲线的三次多项式拟合来确定拐点的方法来确定动态再结晶临界应变(εc)[15]。该多项式如下：

式中，A1、A2、A3、A4为相应变形条件下的常数。

在动态再结晶开始时的临界应变处，有下式成立：

可得：

由于实验钢的实际流变应力曲线并不是数学意义上的光滑曲线，很难直接测量或计算出加工硬化率θ，因此，先将应力-应变曲线进行九次多项式函数进行拟合，再进行微分运算。变形温度1 000℃，变形速率分别为0.01s-1、0.1s-1、1s-1时的lnθ-ε曲线及其三次多项式拟合值如图5，图中箭头所指拐点为开始发生动态再结晶的临界点(εc)。从图中能够看出，实验值和计算值吻合度较高，说明三次多项式拟合可以描述加工硬化率与应变之间的关系。

通过式(12)可以计算变形条件为1 000℃、应变速率0.01s-1、0.1s-1、1s-1时的εc分别为0.095、0.119和0.164。根据峰值应变，可求得对应的εc/εp值分别为0.511、0.511和0.524。通过以上方法，统计不同应变条件时的εc和εp(表2)。可求得εc/εp的平均值如下：

根据临界应变、峰值应变数据及Z参数的计算结果，绘制50Cr5MoV钢动态再结晶lnεp-lnZ和lnεc-lnZ的关系曲线图(图6)。可以观察到，Z参数可以反映临界应变与变形条件之间的规律，且lnε与lnZ呈现较好的线性吻合。通过线性拟合得到动态再结晶临界模型如下：

图5 加工硬化率与应变关系曲线及其三次多项式拟合结果Figure 5 The relation curve between work hardening ratesand strains and its three times polynomial fitting results

温度℃0.01s-10.1s-11s-1εcεpεc/εpεcεpεc/εpεcεpεc/εp9009501000105011000.1070.0980.0950.0820.0760.2050.1910.1860.1550.1510.5220.5130.5110.5290.5030.1350.1260.1190.1080.0950.2650.2450.2330.2120.1910.5090.5140.5110.5090.4970.2110.1720.1640.1420.1280.4250.3430.3130.2770.2550.4960.5010.5240.5130.502

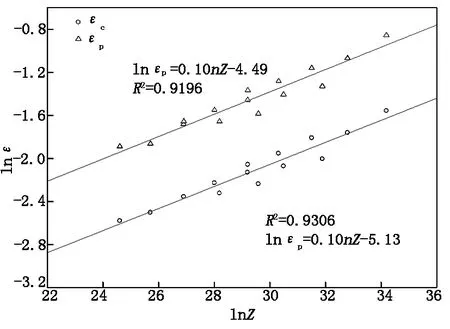
图6 lnεp-lnZ和lnεc-lnZ的关系Figure 6 The relationship between lnεp-lnZ and lnεc-lnZ

3.3 动态再结晶晶粒尺寸模型

动态再结晶过程中，变形工艺对再结晶晶粒尺寸影响很大。当温度升高时，位错的运动比低温时更容易发生，这有利于动态再结晶的形核与晶粒长大[16]。动态再结晶晶粒尺寸Ddrex正比于Z参数的指函数[17]，其表达式为：

其中，C、a为与材料有关的常数。

利用Image tool软件，统计了完全动态再结晶时的晶粒尺寸，计算其平均值(表3)，将不同变形条件下测得的晶粒尺寸d代入式(16)，进行回归处理(图7)，得到不同变形参数下再结晶晶粒尺寸lnDdrex与lnZ呈线性关系，从而求得C=2.64×103，a=-0.159。得出再结晶晶粒尺寸与变形参数之间的模型为：

Ddrex=2.64×103Z-0.159 (17)

图7 lnDdrex与lnZ的关系Figure 7 The relationshop between lnDdrex and lnZ

4 结论

(1)通过热模拟压缩变形实验，可知50Cr5MoV钢存在动态再结晶，并且随着应变速率的降低，形变温度的升高，动态再结晶临界应变量越小，峰值应力越大，再结晶造成的软化越明显。

(2)对热压缩实验数据进行分析，得到50Cr5MoV轧辊钢的动态再结晶激活能为333.47 kJ/mol。

(3)通过对铸态50Cr5MoV钢的动态再结晶行为研究，建立了动态再结晶本构方程、动态再结晶临界应变模型以及动态再结晶晶粒尺寸模型，为大型锻钢轧辊的成型工艺奠定理论基础。

[1] 俞誓达,陈菡.我围轧辊业现状及发展中应注意的问题[J]. 钢铁.2007,42(7):1.

[2] 武建平,贾建平,王自东.V-N微合金化含钨改进型50Cr5MoVW冷轧工作辊用钢[J].特殊钢,2007,28(5):40.

[3] Alexander T, Piotr W, Mihaela A. Modelling the dynamic recrystallization in C-Mn micro-alloyed steel during thermo-mechanical treatment using cellular automata[J] .Computational Materials Science,2014,94:85-94.

[4] 向嵩,谭智林. Q690低碳微合金钢热变形微观组织演变及加工图[J]. 湖南大学学报(自然科学版),2013, 40(4):80-86.

[5] Cao Yu,Di Hong-shuang,Zhang Jin-qi. Research on hot deformation behavior and hot work ability of alloy 800H[J].Acta Metallurgica Sinica, 2013, 7 (49):811-821.

[6] 易啸. 2Cr13钢热变形行为研究[D]. 沈阳: 东北大学材料与冶金学院, 2012 :21-23.

[7] Mcqueen H J,Ryan N D.Constitutive analysis in hot working[J]. Materials Science and Engineering A, 2002, 322:43-46.

[8] Naderi M, Durrenberger L, Bleck W. Constitutive relationships for 22MnB5 boron steel deformed isothermally at high temperatures[J].Materials Science and Engineering, 2008; A478:130.

[9] Zener C, Hollomon J H. Effect of strain-rate upon the plastic flow of steel[J]. J Appl Phys, 1944, 15(1): 22-27.

[10] Mahmoud R, Ghandehari F, Davood N. Modeling the high temperature flow behavior and dynamic recrystallization kinetics of a medium carbon microalloyed steel[J]. ASM International, 2014, 23:1077-1087.

[11] 马博, 彭艳,刘云飞. 低合金钢Q345B动态再结晶动力学模型[J].材料热处理学报, 2010, 31(4): 141-147.

[12] Imbert C A C, Mcqueen H J. Peak strength strain hardening and dynamic restoration of A2 and M2 tool steels in hot deformation[J]. Materials Science and Engineering A, 2001, 313:88-103.

[13] Quan Guo-zheng, Zhao Lei, Shi Yu. An identification and characterization for the dynamic recrystallization critical conditions of Ti-6Al-2Zr-1Mo-1V alloy[J]. Journal of Functional Materials, 2012, 43(2):222-226.

[14] Fen Di,Zhang Xin-ming,Liu Sheng-dan. Rate controlling mechanisms in hot deformation of 7A55 aluminum alloy[J].Transactions of Nonferrous Metals Society of China, 2014, 24:28-35.

[15] Jonas J J,Qujelennec X,Jiang L. Theavrami kinetics of dynamic recrystallization[J]. Acta Materialia,2009,57( 9) : 2748-2756.

[16] 余永宁.金属学原理[M].北京:冶金工业出版社,2003.

[17] Wahabi M E,Cabrera J M,Prado J M.Hot working of two AISI 304 steels: a comparative study[J]. Materials Science and Engineering A,2003,343: 116-125.

编辑 杜青泉

Analysis of Dynamic Recrystallization Behaviour of As-cast 50Cr5MoV Steel

Wang Yaokun, Du Jia, Chen Yang, Li Zhaoku

By using Gleeble-3800 thermomechanical simulator, the hot compression test for as-cast 50Cr5MoV steel has been carried out. Under conditions of the deformation temperature of 900℃, 950℃, 1 000℃, 1 050℃ and 1 100℃ and the strain rate of 0.01 s-1, 0.1 s-1, 1 s-1, the dynamic recrystallization behaviour of steel has been studied. The results show that the dynamic recrystallization appears during the hot deformation process of as-cast 50Cr5MoV steel. And the dynamic recrystallization is more likely to appear along with the reducing of the strain rate and the increasing of the deformation temperature.

as-cast 50Cr5MoV steel; dynamic recrystallization; constitutive equation; critical strain model

2016—09—01

王耀琨(1964—)男，本科，高级工程师。

TG111.7

B