基于水气二相流的边坡降雨入渗有限元分析

习念念，童富果，刘 刚，程庆超

(1.三峡大学 水利与环境学院，湖北 宜昌 443002； 2.湖北省水利水电规划勘测设计院，武汉 430064)



基于水气二相流的边坡降雨入渗有限元分析

习念念1，2，童富果1，刘 刚1，程庆超1

(1.三峡大学 水利与环境学院，湖北 宜昌 443002； 2.湖北省水利水电规划勘测设计院，武汉 430064)

为揭示边坡降雨入渗基本规律，基于水气二相流理论，以三峡库区大坪滑坡为例，采用有限单元法分析边坡降雨入渗水气运动规律。结果表明：根据水气流入、流出的方向不同，坡表可分为吸入区和溢出区，通常坡体上部为水、气吸入区，下部为水、气溢出区；水、气进出坡表的总速率受降雨特性、坡面产流情况、气温变化等外在因素的影响较小，具有相对稳定性；在坡表吸入区，当降雨强度大于水气入渗总速率时，入渗强度等于水气入渗总速率，吸入区产流；反之，入渗强度等于降雨强度，吸入区不产流。此外，坡表饱和区水压力可通过孔隙气传递到地下水面，增大地下水的压力水头，不利于坡体稳定。

水气二相流；降雨入渗；有限单元法；非饱和渗流；三峡库区边坡

1 研究背景

边坡降雨入渗是一个复杂的非饱和渗流过程，其入渗强度主要取决于水、气两相流体在土体中的耦合驱动效应[1]，并与土体渗透性、水气黏滞性以及坡面边界条件等因素有关。以往研究[2-4]大多基于Richard方程来描述降雨入渗，因其假定孔隙气压恒定且处处相等(通常设为大气压)，实质上忽略了水、气耦合作用，仅考虑了水的运动，在特定情况下可能会与工程实际情况出入较大。大量研究成果表明，在边界封闭条件下，孔隙气对液相(水)流动的影响不可忽略[1,5-6]。雨水入渗过程中，土体中空气受液相(水)的挤压而产生与水体运动方向相反的顶托力，进而雨水入渗速率会因水压力梯度的减小而降低。唐海行等[7]，彭胜等[8]，孙冬梅等[9]学者考虑气相影响，实现了边坡降雨的水、气入渗过程，认为采用水气二相流理论探究边坡降雨入渗问题更符合实际。目前国内关于二相流的研究主要探究入渗过程中压力等参数变化，验证了气相的影响，较少涉及降雨入渗规律的一般归纳。本文基于水气二相流的基本理论及方法，对降雨入渗条件下的三峡库区大坪滑坡进行模拟分析，以研究边坡降雨入渗的一般规律，是对现有降雨入渗规律的补充，为工程实例提供更多依据。

2 水气二相流控制微分方程

水气二相流控制微分方程包含液相(水)流动方程和气相流动方程，两者通过饱和度、孔压、基质吸力、孔隙率等参变量的关联性来实现水气二相流耦合描述。水、气在土体孔隙中的流动需各自满足压力驱动下的质量守恒方程，同时考虑土体变形、水气的可压缩性、黏滞性以及饱和度变化等因素，即可得水气二相流控制微分方程[10]

(1)

(2)

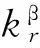
水气二相流控制微分方程是基于时间和空间的非线性偏微分方程组，求解时需先进行时间和空间离散，然后通过迭代求解。本计算空间离散化采用Garlerkin有限单元法，时间离散采用差分法。计算时孔隙气压pg和饱和度S为未知量，通过对方程(1)、方程(2)循环计算以实现迭代求解。

3 数值计算模型

3.1 工程概况及几何模型

本研究以三峡库区大坪滑坡为案例进行计算，大坪滑坡位于巴东县境内长江北岸，上距巴东县城3km，下距三峡工程坝址61km。该滑坡体物质主要为松散岩石碎屑层和黄土层，透水性好，有利于地下水的下渗，滑坡体底部为千枚岩，透水性相对较弱，容易形成相对隔水层。同时滑体物质厚度较大，为滑坡提供了物质基础。大坪滑坡体前缘宽1 100m，后缘宽800m，纵向(顺坡向)长550m，后缘分布在高程280～338m一线，总体呈弧形。取其主滑动剖面进行数值建模，剖面水平长度为600m，竖直向高度为350m。为较好地模拟降雨入渗，网格剖分时滑坡体表层采用厚度较小单元，其厚度沿坡体深度方向按0.25，0.5，0.75m逐渐增加。剖分所得有限元计算网格如图1所示，共计3 499个单元，3 427个节点。

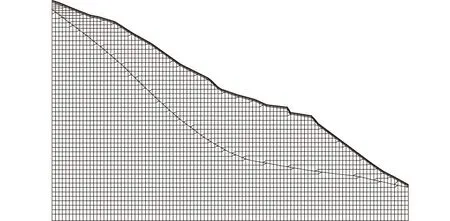
图1 大坪滑坡有限元分析网格

3.2 初始及边界条件

为尽可能减小初始状态不确定性对研究带来的影响，本分析结合三峡库区多年降雨实测资料(由国土资源部三峡库区地质灾害防治工作指挥部提供)，以坡体全饱和态起算，计算模拟至坡体渗流场相对稳定，取其稳定后的渗流场为计算的初始条件。

模型后缘侧面及底部为不透水边界，该边界水位及其变化情况可由计算得到。库水位以下部分坡表面及前缘侧面为已知水压边界，其数值大小取决于库水位高程(库水位高程为145m)。库水位以上坡表为已知气压力边界，鉴于坡面径流水头相较于大气压力相对很小，可忽略，本计算中气压力边界上的气压力均设为大气压。与传统单相流计算相比，坡表水、气入渗率可由计算结果得出，不需要作为流量边界而事先给定。

3.3 主要本构关系和参数

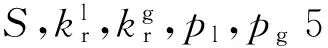
本文土水特征曲线采用常用的VanGenuchten(1980)模型[11]，基质吸力(pc≡pg-pl)与饱和度的关系可表示为

pc=-p0(Se-1/λ-1)1-λ。

(3)

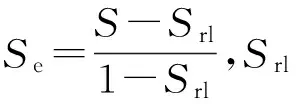
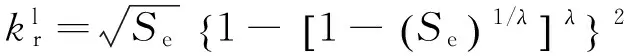
(4)

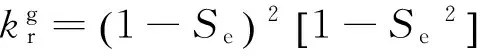
(5)

式(1)、式(2)中涉及的其他主要参数及其数值分别为n=0.15，k=4.0×10-12m2，g=9.8N/kg，ρg=1.29kg/m3，ρl=1×103kg/m3，μl=1.0×10-3N·s/m2，μg=1.0×10-5N·s/m2。

4 边坡降雨入渗分析

降雨入渗是一个非饱和渗流过程，基于水气二相流有限元计算可获得坡体孔隙气压、水压、水饱和度等随时间空间的变化情况，基于分析需要，可绘制任意时刻等值线分布图(如图2)。考虑气相影响后，降雨入渗过程并非传统中的均匀下渗，降雨初期，孔隙气压较小，降雨入渗强度相对较大，随着降雨历时增加，浅层坡体含水量增加，坡表逐渐饱和，降雨入渗强度会随孔隙气压增大而逐渐减小。地下水位会受降雨强度、降雨历时、降雨间隔等因素影响，并在时间上具有一定的滞后性。坡度变幅不大的情况下，饱和区的孔隙水压力与距地表深度正相关，非饱和区的孔隙水压力受初始条件、边界条件等因素影响与距地表深度之间关系不显著。

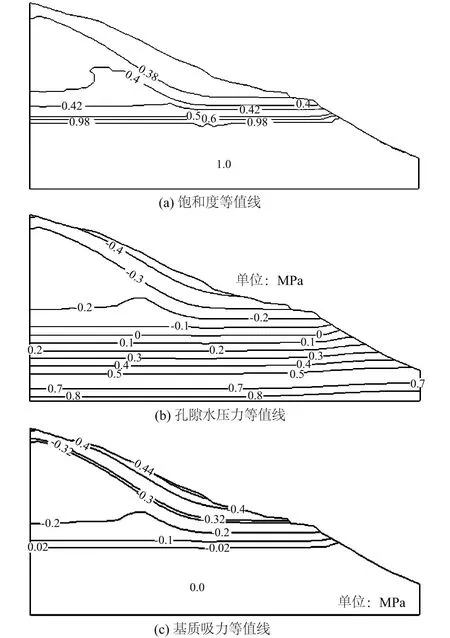
图2 大坪滑坡某时刻等值线分布

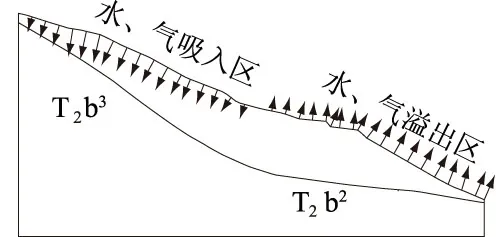
图3 坡表(水、气)吸入、溢出区

结合大坪滑坡水气两相流有限元计算结果，本文先从坡表降雨入渗特性、降雨入渗强度和产流条件等方面阐述边坡降雨入渗一般规律，然后就边坡内水气耦合传力机制进行说明。

4.1 坡表降雨入渗特性

根据大坪滑坡计算结果，物质(水、气)进出坡表的方向和总速率呈现一定规律性。按照物质(水、气)流入、流出方向不同，坡体表面可分为吸入区和溢出区，水气流速方向大体朝坡内则为吸入区，反之则为溢出区(见图3)。分析表明，坡表吸入区和溢出区分布具有较强的规律性，水、气吸入区通常位于滑坡体中上部位，而溢出区一般位于其下部。吸入区和溢出区的分界线通常不是固定的，除与坡体几何特性、渗透特性有关外，还会受降雨历时、降雨间隔、降雨强度等降雨特性的影响。随降雨持续时间的延长，吸入区和溢出区的分界线会上移，坡表吸入区面积会缩小，溢出区面积会增加；随降雨间隔的增加，分界线会逐渐下移，坡表吸入区面积会增大，而溢出区面积会逐渐减小。

从数值上分析，水、气进出坡表的总速率具有相对稳定性，其大小主要取决于坡体几何形态尺寸和岩土材料传输特性，受降雨特性、坡面产流情况、气温变化等外在因素的影响相对较小。水气进出坡表的速率可描述降雨吸入、溢出强度，图4为大坪滑坡坡表水、气吸入(溢出)强度与时间关系。曲线显示，随降雨历时增加，大坪滑坡坡面最大吸入、溢出强度均具有一定的稳定性，最大吸入强度约为0.4mm/min，最大溢出强度约为0.5mm/min。坡面水、气平均吸入和溢出强度值总体均呈平缓下降趋势，两者在数值大小上非常接近，均约为0.1mm/min。

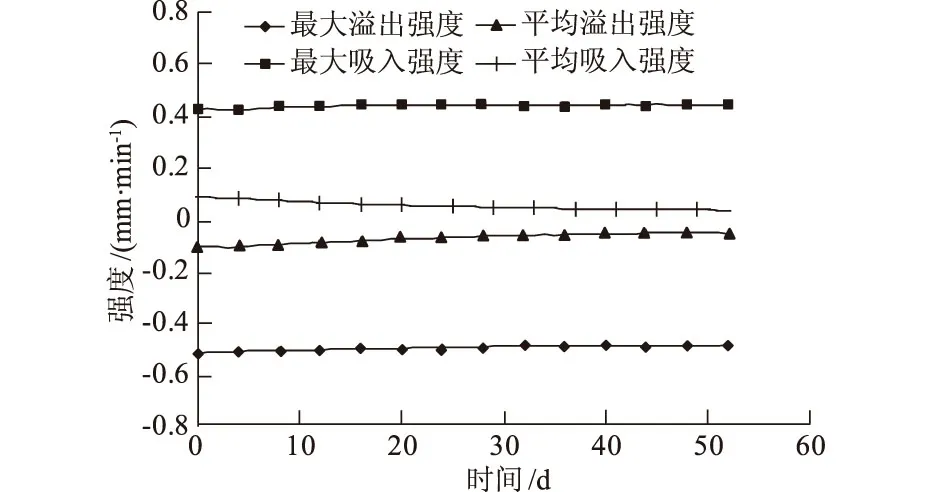
图4 坡面水气吸入、溢出强度时间关系曲线

4.2 坡表降雨入渗强度和产流条件

坡表降雨入渗强度和产流条件的判断与降雨强度和坡面(水、气)总吸入速率的相对大小关系密切。在坡表吸入区，水气入渗量主要取决于坡面边界水、气的含量。在地表无降雨的情况下，吸入区边界吸入的是空气，地表有降雨情况下，降雨强度小于坡面(水、气)总吸入速率时吸入区坡面不产流，雨水入渗强度等于降雨强度，吸入区边界将吸入不同含量的水、气混合物。降雨强度大于坡面(水、气)总吸入速率时，坡面会有径流产生，入渗强度等于水、气总吸入强度，坡表气封，吸入区边界吸入的是水。大坪滑坡案例中，降雨强度大于坡面总吸入强度(约为0.1mm/min)将是其坡面产流的必要条件，由于最大吸入区位于坡顶，故当降雨强度大于坡表最大吸入强度(0.4mm/min)时，坡面才会有全面产流的可能。

在坡表溢出区，水气溢出量除与坡面边界水、气的含量有关，还与坡体饱和度紧密相关。在饱和状态下，降雨入渗强度为0，坡表产流，溢出区边界流出的是水；非饱和状态下，降雨入渗强度等于降雨强度，坡表不产流，溢出区边界流出的是水、气混合物，若在完全干燥的情况下，溢出区边界溢出的是孔隙气。

4.3 水气耦合传力机制

图5 水气耦合传力机制示意图

降雨入渗是水、气两相流体在土体孔隙中相互驱动耦合作用的过程，受重力的作用水体向下运动，进而驱动孔隙气也向下运动，空气因为挤压产生与水体运动方向相反的顶托力。由于空气的黏滞性非常小(约为水的1%)，坡表降雨饱和区水压可通过孔隙气快速传递到地下水面，使地下水面承压(如图5)，表现了气体作用对边坡稳定的不利影响。图6是大坪滑坡某时刻的饱和度分布云图，由图可见，坡体顶部的饱和水压力会经非饱和区内封闭的孔隙气传到滑坡体前端饱和区，局部抬高坡体前沿阻滑区的地下水位，形成不利坡面稳定的外法向推力。

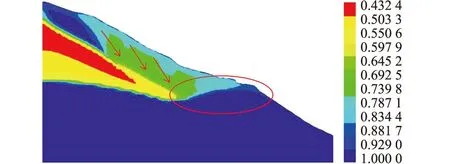
图6 大坪滑坡饱和度分布云图(传力示意)

5 结 论

本文基于水气二相流理论，采用有限元法计算分析了大坪滑坡体降雨入渗过程。结果表明：①根据水、气进出坡体的方向不同，坡体表面可分为吸入区和溢出区，通常吸入区位于坡体表面中上部，溢出区位于其中下部；②水、气进出坡表的总速率主要取决于坡体材料传输特性和几何特性，受坡面产流情况和径流深度影响较小，具有一定的稳定性；③降雨强度和水、气总吸入速率的相对大小关系可作为坡表降雨入渗强度和产流条件的判断条件。在坡表吸入区，当降雨强度小于坡面水、气总吸入速率时不产流，入渗强度等于降雨强度；反之，坡面产流，入渗强度等于水、气总吸入强度；④坡体表层饱和区水压力可通过非饱和区的孔隙气传递到地下饱和区，使地下水面承压，增大了坡脚外法向推力，不利边坡稳定。

本计算通过模拟分析降雨入渗一般规律，为工程实例提供了更多理论依据。因影响降雨入渗过程因素众多，故对入渗规律的定量分析较少，拟在后续研究中，分析控制各影响因素，深入量化入渗过程的一般规律。

[1] 徐 晗，朱以文，蔡元奇，等.降雨入渗条件下非饱和土边坡稳定分析[J].岩土力学， 2005,(12):1957-1962.

[2] 周家文，徐卫亚，邓俊晔，等.降雨入渗条件下边坡的稳定性分析[J].水利学报，2008，39(9):1066-1073.

[3] 荣 冠，张 伟，周创兵，等.降雨入渗条件下边坡岩体饱和非饱和渗流计算[J].岩土力学，2005，26(l0):1544-1550.

[4] 朱 伟，陈学东，钟小春.降雨入渗规律的实测与分析[J]. 岩土力学， 2006， 27(11): 1873-1879.

[5]LALOUIL,KLUBERTANZG,GULLIETL.Solid-liquid-airCouplinginMultiphasePorousMedia[J].InternationalJournalforNumericalandAnalyticalMethodsinGeomechanics, 2003,27:183-206.

[6] 王叶娇， 曹 玲， 徐永福. 降雨入渗下非饱和土边坡临界稳定性分析[J].长江科学院院报， 2013， 30(9): 75-79.

[7] 唐海行，苏逸深.考虑气压势影响的降雨入渗数值模拟研究[J].水科学进展， 1996,(7):8-13.

[8] 彭 胜，陈家军，王金生，等.包气带水气二相流国外研究综述[J].水科学进展， 2000,(3):333-338.

[9] 孙冬梅，朱岳明，张明进.降雨入渗过程的水-气二相流模型研究[J].水利学报， 2007,(2):150-156.

[10]TONGFG，JINGL，ZIMMERMANRW.AFully-coupledFiniteElementCodeforModelingThermo-hydro-mechanicalProcessesinPorousGeologicalMedia[C]∥Proceedingsofthe43rdUSRockMechanicsSymposium,Asheville,NC,USA,June28-30, 2009: 28-30.

[11]VANGENUCHTENMTH.AClosedFormEquationforPredictingtheHydraulicconductivityofUnsaturatedSoil[J].SoilScienceSocietyofAmericaJournal,1980, 44(5): 892-898.

[12]MUALEMY.ANewModelforPredictingtheHydraulicConductivityofUnsaturatedPorousMedia[J].WaterResourcesResearch, 1976, 12(3): 513-522.

[13]COREYAT.TheInterrelationBetweenGasandOilRelativePermeabilities[J].ProducersMonthly, 1954, 19: 38-41.

(编辑：刘运飞)

Finite Element Analysis of Water-air Two-Phase Infiltration in Slope

XI Nian-nian1，2, TONG Fu-guo1, LIU Gang1, CHENG Qing-chao1

(1.College of Hydraulic and Environmental Engineering, China Three Gorges University,Yichang 443002, China； 2.Hubei Provincial Water Resources and Hydropower Planning Survey and Design Institute, Wuhan 430064,China)

On the basis of the theory of two-phase (water and air) flow, the law of water-air movement caused by rainfall infiltration in slope was revealed by means of finite element method. Daping landslide in Three Gorges Reservoir was taken as a case study. The simulation results show that the slope surface can be divided into the inflow area and the outflow area according to the inflow and outflow of water and air. Usually the upper part of slope is inflow area, and the lower part is outflow area. The total infiltration rate of water and air in slope is relatively stable, slightly affected by rainfall characteristics, slope surface runoff and temperature changes. In the inflow area, when rainfall intensity is greater than infiltration rate, water in slope will run off, otherwise water or air will completely infiltrate. The saturation pressure of slope surface could transmit to groundwater surface through pore air, which increases the groundwater pressure head, unfavorable for slope stability.

water-air two-phase flow; rainfall infiltration; finite element method; unsaturated seepage; slope in Three Gorges Reservoir

2015-11-16；

2016-02-02

国家自然科学基金项目(51279090)

习念念(1990-)，女，湖北襄阳人，硕士研究生，主要从事水工结构水气二相流耦合问题方面的研究，(电话)15090906272(电子信箱)nn_ctgu@163.com。

童富果(1972-)，男，湖北宜昌人，教授，博士生导师，主要从事水工结构和岩土工程领域多场耦合(THMC)问题及其数值方法方面的研究，(电话)13972560499(电子信箱)tfg@ctgu.edu.cn。

10.11988/ckyyb.20150975

2017,34(1):120-123，141

TV139.1

A

1001-5485(2017)01-0120-04