扩散型梯形翼墙消力池最不利消能工况计算研究
2017-02-05黄朝煊方咏来李水泷
黄朝煊,方咏来,李水泷
(浙江省水利水电勘测设计院,杭州 310002)
扩散型梯形翼墙消力池最不利消能工况计算研究
黄朝煊,方咏来,李水泷
(浙江省水利水电勘测设计院,杭州 310002)
针对目前消能计算大多适用于矩形断面情况,根据水力学理论、数学函数理论及无量纲原理对扩散型梯形翼墙水闸最不利消能工况进行研究,推导出扩散型梯形断面相对收缩水深、相对跃后水深的解析计算公式。通过Matlab软件数值分析及数学推导给出了受潮位影响的沿海挡潮排涝闸消力池池深极值、水跃长度极值的简捷计算公式,并通过工程实例计算比较,该解析计算式方便简捷、精度可靠。
工程水力学;水闸;最不利消能工况;扩散型梯形翼墙;消力池池深;水跃长
1 研究背景
随着国家对城市防洪排涝的重视、“五水共治”以及“海绵城市”理念的提出,水闸消能计算显得尤为重要。目前现有水闸消能计算公式只针对矩形断面,对于梯形翼墙断面消能不再适用。如文献[1]中舟山市六横小郭巨围垦工程挡潮排涝闸由于外海潮位不停变化,矩形闸门内外水压波动,闸门周边橡皮止水水封不密实,渗漏很严重。浙江省水利水电勘测设计院创新性地提出了梯形闸门,该型闸门水密性很好,可完全解决挡潮排涝闸的渗漏问题。因此,本文对扩散型梯形翼墙断面水闸消能计算进行了深入研究。
《水闸设计规范》[2]等多数文献对水闸消能计算的研究均是分析在给定某一特定消能工况下的消力池深计算方法,需先计算闸后的收缩断面水深h1、相应于收缩断面水深h1的水跃共轭水深h2以及出水池落差ΔZ,然后根据几何关系求出消力池深度d。由于在计算收缩断面水深h1时消力池深度d值尚未确定,因此势必先假定不同的消力池深度d来反复进行试算,才能得出满足要求的d值。黄朝煊等[3]对矩形断面消力池池深极值进行了无量纲化数学推导,得出了矩形断面消力池池深极值的直接计算公式;谢景惠等[4]也对矩形断面消力池池深计算进行了微分极值初步推演,但不具备实际应用价值。
田嘉宁等[5]、Bakhtyar等[6-7]采用智能算法如遗传算法(GA)和粒子群算法(SPO)等对多级消力池总长等参数进行了程序优化,但其原理与罗列多工况试算法基本一致。田嘉宁等[8]、刘璐等[9]通过试验模型对消力池进行了研究,但不能得出通性规律。
鉴于当前对水闸消力池计算仅适用于矩形断面并且最不利工况寻找较困难,本文通过数学分析理论,结合Matlab软件及CurveExpert拟合软件对扩散型梯形翼墙断面消力池最不利消能工况进行深入研究。
2 消能计算基本理论
消力池消能计算基本公式为
(1)
式中:d为消力池深度(m);T0为以收缩断面底部为基准面的泄水建筑物上游总水头(m);h1为收缩断面水深(m);h2为跃后水深(m);hs为下游河床水深(m);Q为流量(m3/s);g为重力加速度常数(m/s2);φ为流速系数;A1为收缩断面过水面积(m2);As为下游河床过水断面面积(m2);A2为跃后过水断面面积(m2);Lsj为消力池长度(m);Ls为消力池斜坡段水平投影长度(m);Lj为水跃长度(m);β为水跃长度校正系数,可采用0.7~0.8;σ0为水跃淹没系数,可取1.05~1.10。
其中跃后水深h2可根据水跃动量方程求解,后文将具体给出计算公式。消力池消能见图1。
3 梯形断面水跃特征水深计算
3.1 跃前收缩水深计算

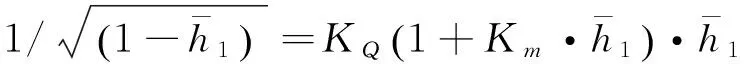
(2)
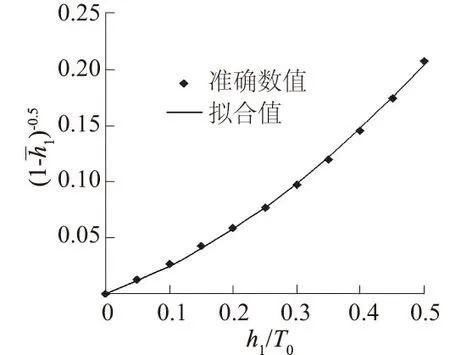
图2 函数高精度二次曲线拟合
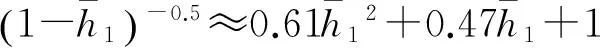
代入收缩水深计算式(2)左边,求解一元二次方程可得收缩水深计算式为
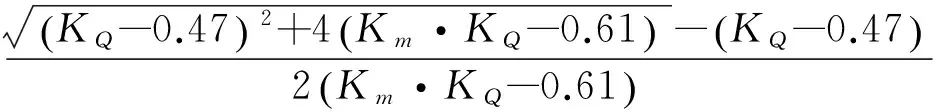
(3)
式(3)最大相对误差<0.15%,精度完全满足工程计算要求。
3.2 跃后共轭水深计算
对于扩散型梯形翼墙断面下水跃共轭水深的计算,利用连续方程和动量方程推导可得水跃方程式为
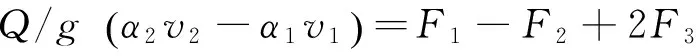
(4)
式中:v1,v2为跃前断面和跃后断面平均流速;g为重力加速度;α1,α2为跃前断面和跃后断面流速系数;F1,F2为跃前断面和跃后断面顺水流轴线方向作用力;F3为扩散段翼墙水压力在顺水流轴线方向的投影分量值。扩散型梯形断面消能见图3。
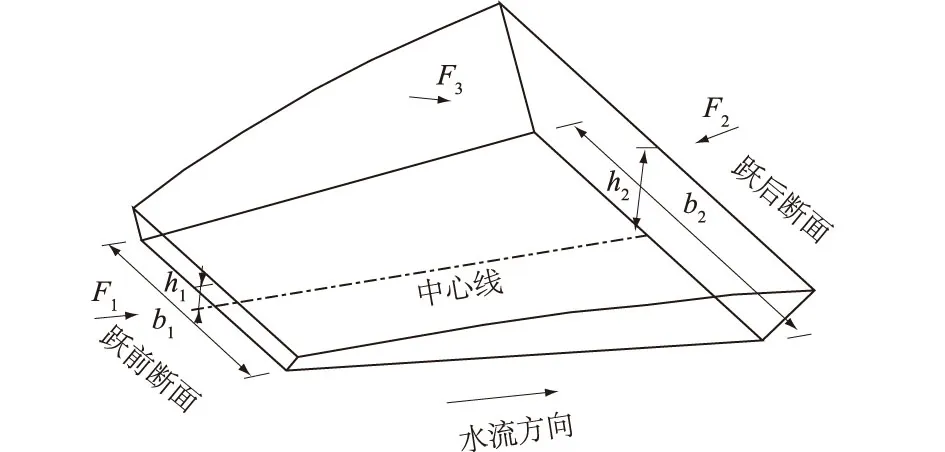
图3 扩散型梯形断面消能
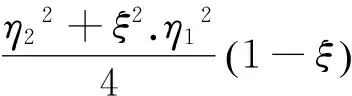
(5)
式(5)即为根据跃前收缩水深计算水跃后共轭水深的计算方程,该方程也是一元五次方程,一般情况下无法得出公式解。
3.2.1 无扩散时(ξ=1)跃后共轭水深计算
当无扩散时,即b1=b2=b时,ξ=1,式(5)可进一步简化为
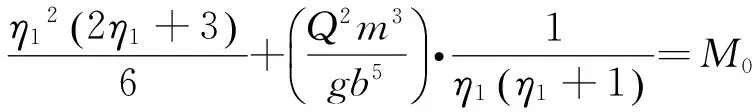
(6)
易知式(6)是对称方程,η1,η2均是一元五次对称方程(6)的实根,可转化为一元四次方程,便能求出其解析解。
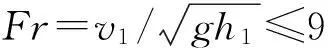
通过数学理论推导及最佳逼近拟合原理,得出无扩散时(ξ=1)共轭水深的计算式,即
y=(-0.519x2+2.147x)/(x2+0.641x-0.02)。
(7)
3.2.2 扩散型(0.5<ξ<1)跃后共轭水深计算
(8)
式(8)为关于η2的一元五次方程,由于式(8)较复杂,无法直接求解,可采用迭代法求解,其迭代方程由式(8)变换而得,其形式为
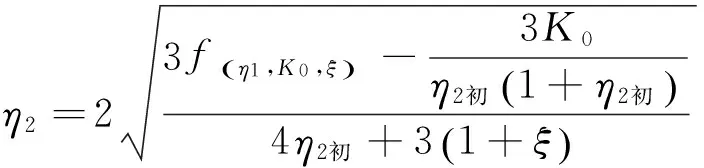
(9)
通过对式(9)右边求导容易证明迭代方程(9)收敛,式(9)右边函数导数绝对值<1,限于篇幅,本文未详细给出证明。
其迭代初值可根据无扩散时(ξ=1)跃后共轭水深的修正值(乘以修正系数ξ)给出,计算式为
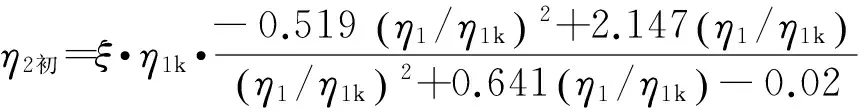
(10)
其中收缩断面的临界水深无量纲值可通过式(11)计算(详见文献[10-11]),即
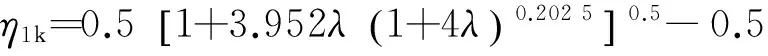
(11)
通过Matlab软件进行大量数值计算分析可知,本文初值计算式(10)精度较高,最大相对误差一般<5%,对式(9)迭代一次后精度基本<1.0%,满足工程实际计算要求。
4 扩散型梯形翼墙消力池最不利消能工况分析
4.1 无量纲化处理
根据无量纲化理论及通常水闸水力参数基本范围可知
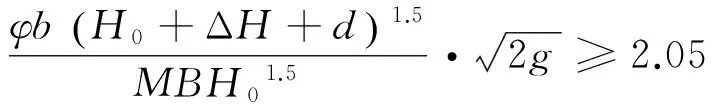
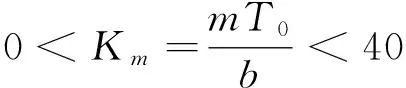
式中ΔH为水闸底板高程与下游河床高程的差值(m)。
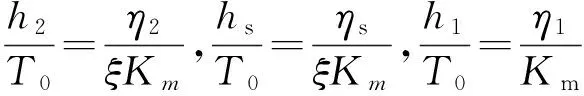
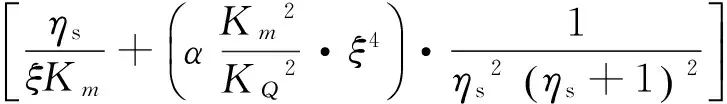
(12)
通过以上分析可知,相对消力池深是关于相对跃后水深η2及相对下游水深ηs的马鞍形曲面。只有当相对跃后水深η2越大并且相应相对下游水深ηs越接近于ηs,cr时,相应的消力池深才取极大值。
值得说明的是:不同地区水闸如沿海挡潮排涝闸、平原水闸以及山区大落差水闸,其相应下游水位的确定方式不同,对消力池最不利池深计算的影响也不同。对于沿海挡潮排涝闸,其下游水位受过闸流量及外海潮位共同影响,且浙闽等沿海地区海床多为淤泥软土,其抗冲能力差,对该型水闸的消能计算需尤其重视;对于平原水闸,其下游水位则需通过相应的过闸流量来确定。
同样,对水跃长无量纲化得
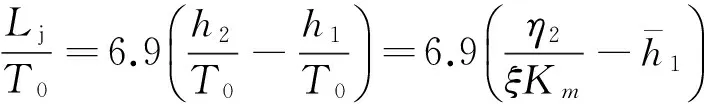
(13)
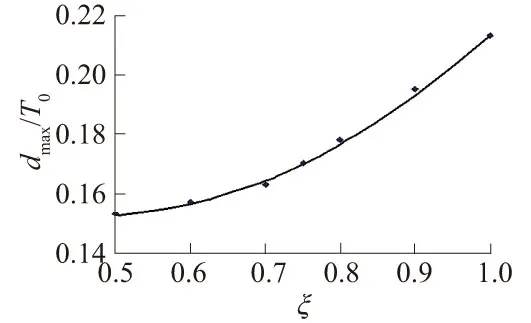
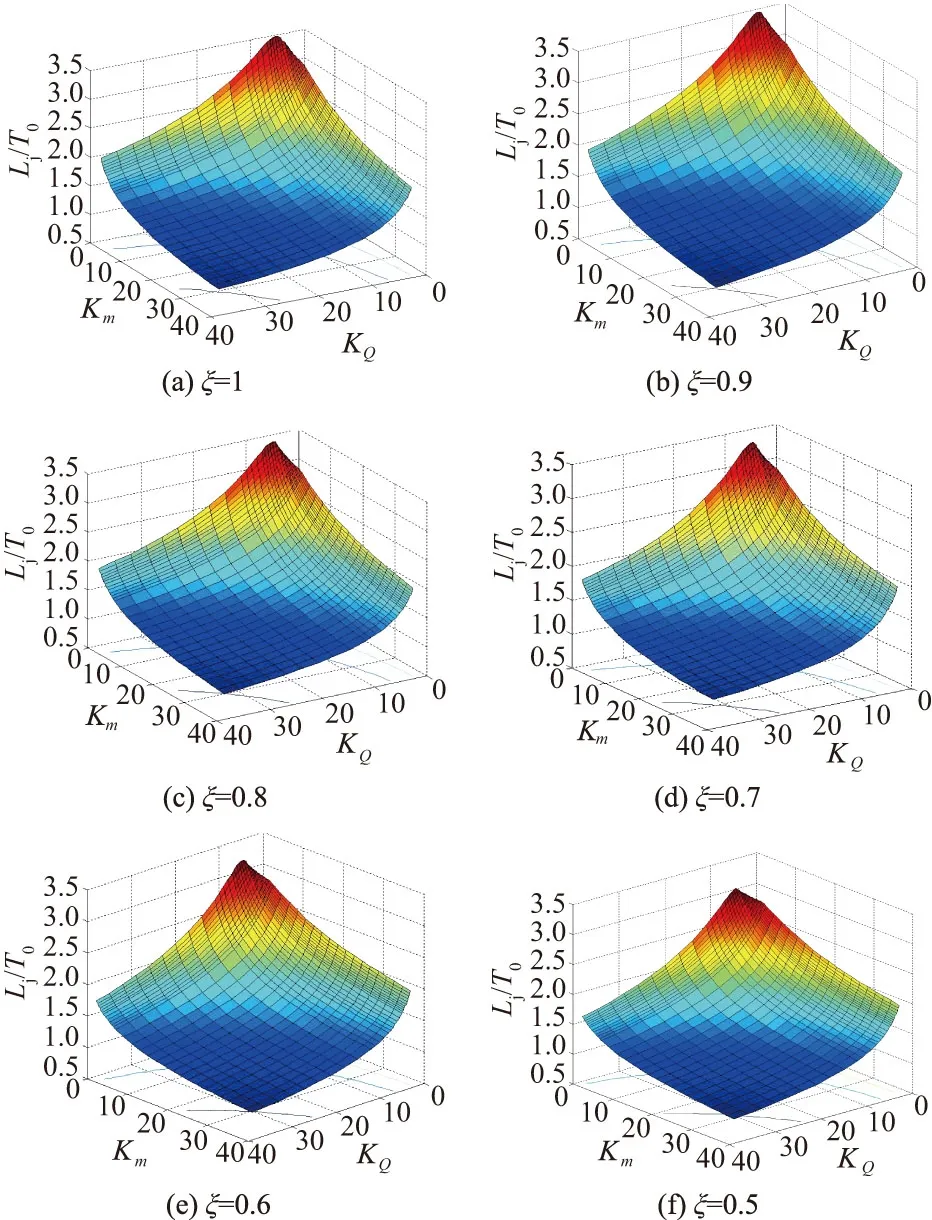
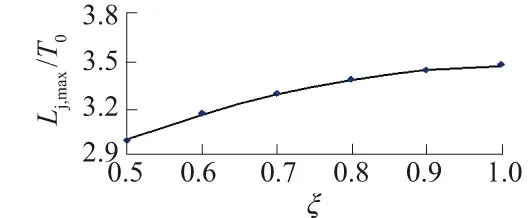
4.2 消力池最不利工况池深、池长计算
对于沿海挡潮排涝闸,由于消力池下游水位随外海潮位影响变化较大,利用式(12)计算该型水闸消力池深时可取最不利的下游水深,即式(12)中后半部分的无量纲函数g(ηs)在有界区间ηs<η2中求最小值。根据前文理论算法,在2 通过式(12)可得到沿海挡潮排涝闸消力池相对池深随无量纲参数KQ,Km,ξ=b1/b2的曲面图,如图4所示。 图4 消力池相对池深d/T0与KQ,Km的曲面关系 图5 消力池相对池深极值 dmax/T0与扩散度ξ的关系 由图4可以得到沿海挡潮排涝闸消力池相对池深极值与扩散度ξ之间的关系,如图5所示。利用Matlab软件及CurveExpert拟合软件,进行数值回归分析,得到消力池相对池深极值简化计算式,即 (14) 将T0=H0+d代入式(14),得到关于消力池池深的方程,即 (15) 式中:dmax为沿海挡潮排涝闸的消力池深(m);H0为闸前水头(m)。 同样,可得到沿海挡潮排涝闸消力池相对水跃长随无量纲参数KQ,Km,ξ=b1/b2的曲面图,如图6所示。由图6可知,相对水跃长Lj/T0在Km,KQ充分大时,随Km,KQ的增大而减小。 图6 消力池相对水跃长Lj/T0与KQ,Km曲面关系图 图7 相对水跃长极值 Lj,max/T0与扩散度ξ的关系 由图6可以得到沿海挡潮排涝闸消力池相对水跃长极值与扩散度ξ之间的关系,如图7所示。利用Matlab软件及CurveExpert拟合软件进行数值回归分析,得到消力池相对水跃长Lj/T0极值的简化计算式,即 (16) 消力池相对水跃长极值计算式(16)与下游水深无关,对3类水闸(沿海挡潮排涝闸、平原水闸以及山区大落差水闸)均适用。 对于平原水闸及山区大落差水闸,其下游水位也需通过相应的过闸流量来确定,若按沿海挡潮排涝闸极值分析,则计算出的消力池深将比实际值稍偏大,其偏大量为[g(ηs) -gmin(ηs,cr)],此时需计算相应流量时的下游水深。 对于下游河道正常水深计算,黄朝煊[11-12]给出了目前精度最好的梯形明渠正常水深直接计算式。 算例:已知某沿海淤泥软基础桩基水闸,闸前断面总水头 T0=10.31m,过闸流量 Q=140m3/s。梯形翼墙消力池断面底宽b1=10m,b2=12.5m,梯形翼墙边坡系数 m=1,流速系数 φ=0.95,试设计闸下消力池池深、池长。 解:假设下游水深hs=4.0m,试计算该工况下消力池池深、池长。 由消能计算式(1)可知 若直接利用本文极值理论计算,由于外海潮位波动较大,计算最不利条件下消力池池深极值为dmax=(0.2ξ2-0.18ξ+0.19)T0=0.173×10.31=1.784m;比本文扩散型梯形翼墙消力池特定工况下的消力池深计算值0.849m大。 由于外海潮位波动较大,则最不利条件下消力池池长极值为Lj,max=(1.64ξ2+3.38ξ+1.73)T0=3.38×10.31=34.85m;消力池池长为Lsj=Ls+βLj=3×1.784+0.8×34.85=33.23m,比本文扩散型梯形翼墙消力池特定工况下的消力池深计算值23.47m大。 鉴于当前水闸消能计算不适用于梯形翼墙断面情况,根据水力学理论及消能基本公式,结合Matlab软件及CurveExpert拟合软件,对含扩散型梯形翼墙的水闸消能最不利工况进行了深入研究,主要结论如下: (1) 通过数学函数理论及无量纲原理对扩散型梯形翼墙断面水闸消能计算进行分析,推导了相对收缩水深直接计算式,该式最大相对误差<0.15%;根据水力学理论及动量原理,推导了扩散型(0.5≤ξ≤1)梯形翼墙断面消力池水跃跃后水深的直接计算式。 (2) 通过Matlab软件编程进行数值分析研究,分别给出了不同扩散度ξ 下,沿海挡潮排涝闸的消力池相对池深d/T0、相对水跃长Lj/T0与KQ,Km曲面关系图,进而通过高精度数值拟合分析,分别给出了梯形翼墙消力池最不利消能工况下消力池相对池深极值、相对水跃长极值的高精度解析计算式,并通过工程算例计算比较,本文解析计算式法精度可靠,方便快捷。 [1] 浙江省水利水电勘测设计院.舟山市六横小郭巨围垦工程初步设计[R]. 杭州:浙江省水利水电勘测设计院,2010. [2]SL265—2001,水闸设计规范[S]. 北京:中国水利水电出版社,2001. [3] 黄朝煊, 王贺瑶, 王正中,等. 消力池最不利条件下池深极值探讨[J].水力发电学报,2015,34(1):79-84. [4] 谢景惠, 陈菊清. 消力池最不利设计条的分析与计算[J]. 水利水电技术, 1995,(12):7-11. [5] 田嘉宁, 安田阳一, 李建中. 台阶式泄水建筑物的消能分析 [J]. 水力发电学报, 2009,28(2):96-100. [6]BAKHTYARR,BARRYDA.OptimizationofCascadeStillingBasinsUsingGAandPSOApproaches[J].JournalofHydroinformatics, 2009,11(2):119-132. [7]BAKHTYARR,MOUSAVISJ,AFSHARA.Dynamic-programmingApproachtoOptimalDesignofCascadeStillingBasins[J].JournalofHydraulicEngineering,2007,133(8):949-954. [8] 田嘉宁, 赵 庆, 范留明. 台阶式溢流坝后消力池压强特性[J]. 水力发电学报, 2012, 31(4): 113-118. [9] 刘 璐, 张建民, 余 飞, 等. 重力坝下游宽尾墩和消力池联合消能工水力特性试验研究 [J]. 水力发电学报, 2012, 31(2): 49-55. [10]黄朝煊. 梯形断面消力池扩散型消能计算[J]. 水利水电科技进展, 2016,36(5):34-39. [11]黄朝煊. 梯形明渠水力学特征水深的解析计算式研究[J]. 灌溉排水学报, 2016, 35(3): 73-77. [12]黄朝煊. 梯形渠道恒定渐变流水面线计算的新解析法[J]. 长江科学院院报, 2012, 29(11): 46-49. (编辑:罗 娟) Calculation of Energy Dissipation for the Most Unfavorable Conditionsof Stilling Basin with Diffusing Trapezoidal Wing Wall HUANG Chao-xuan, FANG Yong-lai, LI Shui-long (Zhejiang Provincial Water Conservancy and Hydropower Survey and Design Institute, Hangzhou 310002,China) Most energy dissipation formula are applicable to rectangular wing wall sections. In view of this, the most unfavorable condition of energy dissipation for diffusing trapezoidal wing of sluice wall was investigated according the hydraulics theory, the mathematical function theory and the dimensionless principle. Analytical formulas of the relative contracted water depth and the relative water depth after jump were deduced.By using Matlab software for numerical analysis and mathematical derivation, simple formulas were given to calculate the extremes of pool depth and water jump length of the stilling basin of coastal tidal drainage sluice influenced by tide level. Through engineering example calculation, the analytic formulas are proved to be convenient with high precision and reliability. engineering hydraulics; sluice; the most unfavorable conditions of energy dissipation; diffusion trapezoidal wing wall; depth of stilling pool; water jump length 2015-09-15; 2015-11-23 水利部公益性行业科研专项项目(201401010);浙水院科标业项目资助(B1608,B1609) 黄朝煊(1983-),男,湖北黄石人,工程师,硕士,主要从事水工结构及岩土工程研究,(电话)13819483276(电子信箱)516227811@qq.com。 10.11988/ckyyb.20150785 2017,34(1):71-76 TV131.4 A 1001-5485(2017)01-0071-06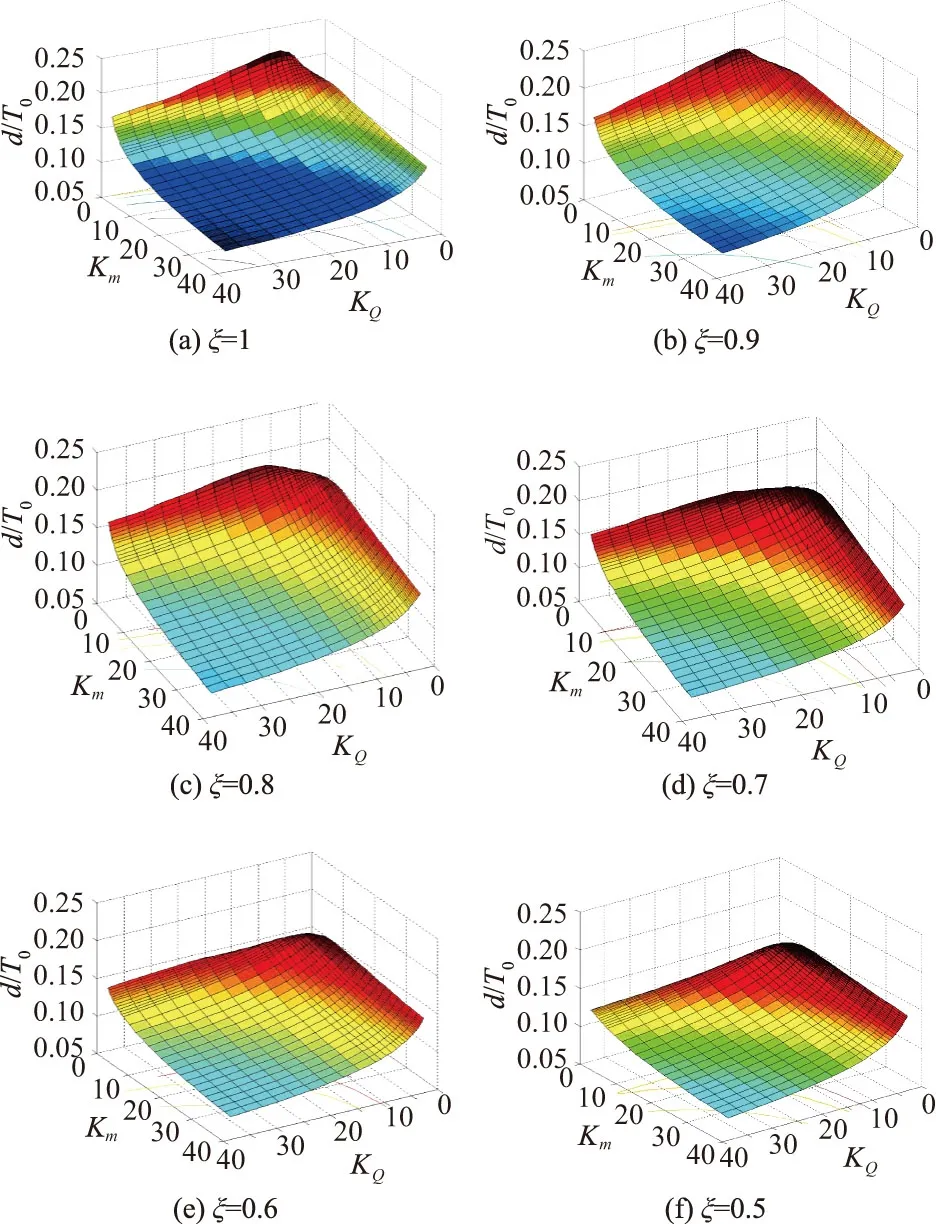
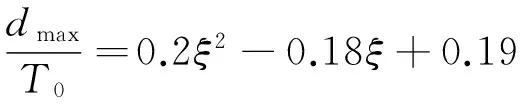
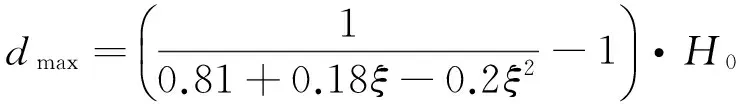
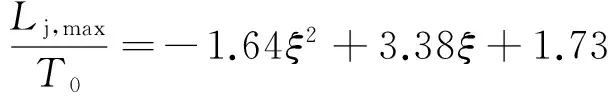
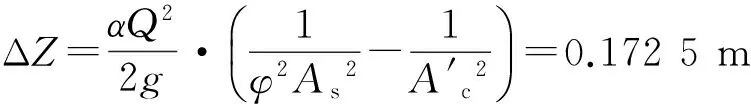
5 结 语
