基于隐马尔可夫模型的安徽省降水特征研究

霍凤岚，张 茜，阿茹娜，刘晓梅，包曙明，吴云飞，包世超，李树森

(1.通辽市防汛抗旱物资供应管理站，内蒙古 通辽 028000； 2.吉林大学 环境与资源学院，长春 130021； 3.内蒙古电力科学研究院，呼和浩特 010020; 4.通辽市水利工程建设质量与安全监督站，内蒙古 通辽 028000; 5.通辽市水利规划设计研究院，内蒙古 通辽 028000)



基于隐马尔可夫模型的安徽省降水特征研究

霍凤岚1，张 茜2，阿茹娜3，刘晓梅4，包曙明5，吴云飞5，包世超5，李树森5

(1.通辽市防汛抗旱物资供应管理站，内蒙古 通辽 028000； 2.吉林大学 环境与资源学院，长春 130021； 3.内蒙古电力科学研究院，呼和浩特 010020; 4.通辽市水利工程建设质量与安全监督站，内蒙古 通辽 028000; 5.通辽市水利规划设计研究院，内蒙古 通辽 028000)

通过隐马尔可夫模型(Hidden Markov Model,HMM)对安徽省降水规律及特征进行分析模拟，以验证其在区域性降水方面的适用性。采用包含4个隐式状态的HMM对省内6个主要城市的多年日降水数据序列进行拟合。用贝叶斯信息准则(Bayesian Information Criterions,BIC)确定模型中隐式状态数量，用Baum-Welch算法训练得到最优模型参数，用Viterbi算法确定模型中最优状态序列。采用上述方法模拟安徽省6个城市在1960—2009年夏季共50个时段的降水情况。前40 a用于模型分析训练，后10 a用于模型验证及评价，结果表明HMM能更好地模拟降水特征，具有较高的实用性。

隐马尔可夫模型；隐式状态；降水特征；贝叶斯信息准则；Baum-Welch算法；Viterbi算法

1 研究背景

降水随机模型具有很多重要的应用，如指导干旱及洪涝灾害预防、预警异常天气、分析径流量及规划农业用水等。长期日降水序列是降水随机模型的重要组成部分，有助于更好地理解和管理水资源、环境及生态系统。由于降水产生机制具有很多不同形式(如地理位置、大气环流等)并且表现出不同特征，因此单一降水随机模型难以较好地表现多状态条件下的降水序列。隐马尔可夫模型假设存在隐含状态，这些状态决定降水产生机制，控制着降水预测中的相关参数。

本文基于隐马尔可夫模型(HMM)在大气模式、地理位置、人类活动等影响因素下模拟未来降水。HMM最初是在20世纪60年代由Leonard 等人提出，其最初的应用之一是20世纪70年代中期的语音识别。在1980年代后半期，HMM开始应用到生物序列的分析中。

HMM被诸多学者广泛应用于降水模拟领域。Hughes和Guttorp[1]构建了一个非齐次隐马尔可夫模型，将多站点降水发生情况与较大区域的大气循环模式相联系，尽管大气循环等影响因素在不同时间段存在变化，模型生成的降水序列与降水序列多年观察值还是拟合较好；Thyer和Kuczera[2]用基于单站点降水数据的HMM模拟了长期水文-气象时间序列并重新生成较可靠的天气干湿周期； Thyer等[3]指出了HMM模拟长时间降水序列能产生较准确的作为水文时间序列重要特征的天气干、湿周期；Hajo和Axel提出时间序列的循环变动现象，并在此基础上构建了改进的HMM[4]；Constantin和Heike等人在统计降尺度方法的基础上，将欧洲及大西洋大气循环过程加以分析处理，构建了基于19个站点7个隐式状态的HMM来预测多瑙河盆地春季降水[5]。

隐马尔可夫模型具有产生长期天气干湿状态周期的明确机制，这是许多长期水文时间序列的一个特性。应用HMM模拟预测日降水的关键在于隐式状态与可观察序列的良好合理对应。充分评估基于多雨量站点的HMM中参数的不确定性，这是长期水文时间序列随机模型的一个进步。本文用贝叶斯方法充分量化HMM中参数的不确定性，然后基于多站点降水数据模拟长期降水时间序列。多站点相对于单一站点模拟具有诸多优势，比如单一站点模型不足以支持大型水资源管理系统，而多站点模型对大区域的干旱洪涝风险模拟程度更高。同时与以前研究中通过无偏灰色马尔可夫模型计算的结果进行对比，结果表明HMM模拟的相对误差更小，能更好地模拟降水特征，具有较高的实用性。

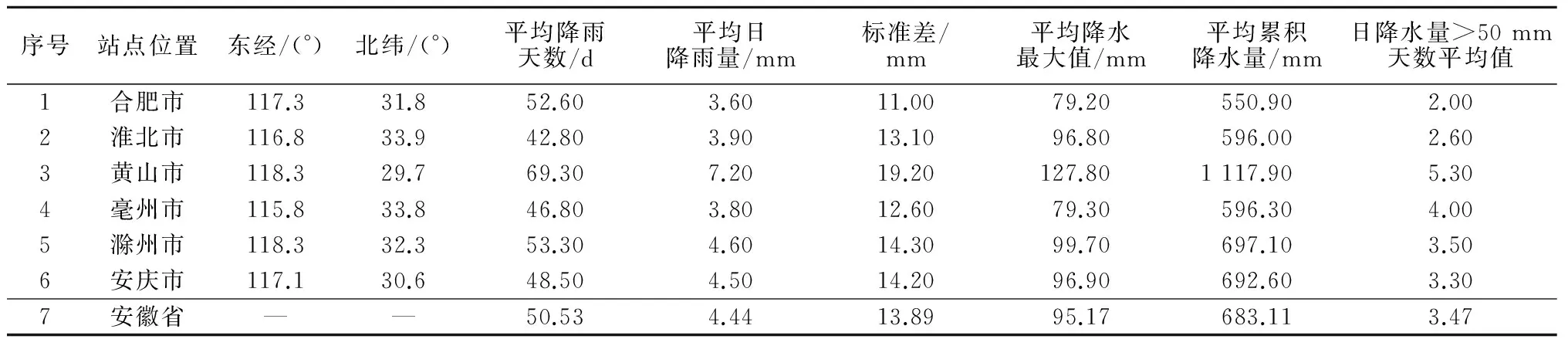
表1 1960—1994年(6—10月份)各站及安徽省主要降水特征

2 研究区概况

安徽省是位于中国东部内陆的一个省份，介于东经114°54′～119°37′，北纬29°41′～34°38′，地貌以平原、丘陵和低山为主。长江淮河流经省内，将全省区域划分为淮北、江淮之间和江南3个区域。安徽省在气候上属暖温带与亚热带的过渡地区，在淮河以北属暖温带半湿润季风气候，淮河以南属亚热带湿润季风气候。省内降水量受地形及气候的影响，时空分布不均，丰枯变化悬殊，夏季降雨集中，冬季雨水较少。总的趋势是由南向北递减, 西部多于东部, 山区多于平原, 山地迎风坡多于背风坡。全年平均降水量为773～1 670 mm，夏季降水丰沛，占年降水量的40%～60%。

本文数据选取自安徽省6个雨量站点，分别位于合肥市、淮北市、黄山市、毫州市、滁州市和安庆市，雨量站位置分布见图1。

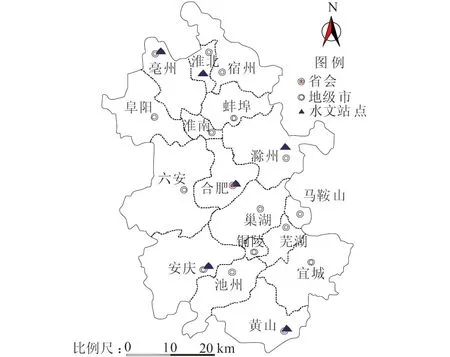
图1 雨量站位置分布

6个站点分别位于省内不同地理位置，由点及面概括全省，通过泰森多边形法求得全省面降水量，并对其进行特征分析，这对全省范围内的降水规律研究有较好的参考性。

根据安徽省1960—2009年的降水数据统计，每年的6—10月份为降水最为集中且降雨量较大的时期，因此选取这段时间作为模型模拟的时间序列区间(153 d/a)，每站点各有50个降雨统计周期。前40 a(共6 120 d)数据用于模型构建及参数训练，后10 a(共1 530 d)数据用于模型验证及评价。研究区的降水数据具有完整性及可靠性，可以得到降水序列的内部特征概况及时空持续性。研究区各站点及全省多年降水特征概况见表1。

3 隐马尔可夫模型

隐马尔可夫是一个双重随机过程，我们不知道具体的状态序列，只知道状态转移的概率，即模型的状态转换过程是不可观察的，而可观察事件的随机过程是隐蔽状态转换过程的随机函数。HMM主要由5个部分构成，分别为模型中状态数量、每个状态对应可能输出的观察值、状态转移概率矩阵、从状态产生观察值的概率分布矩阵和初始状态的概率分布。隐马尔可夫模型框架见图2。

图2 隐马尔可夫模型框架

如图2所示，S表示模型中的隐式状态，即控制输出观察值的内部状态；O表示特定隐式状态下的观察值。本文中观察值解释为天气晴雨状况，隐式状态为决定该地区天气晴雨状况的内部状态。隐马尔可夫模型是在3个前提下得到的，这3个假设条件如下。

(1) 马尔可夫假设：隐式状态构成一阶马尔可夫链。

(2) 不动性假设：当前状态与时间无关，只取决于上一个状态和状态转移概率矩阵，表示为

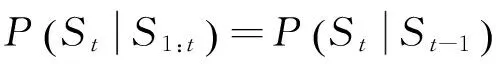
(1)

(3) 输出独立性假设：输出的观察值仅与当前隐式状态有关，与之前其他时刻状态及观察值无关，表示为

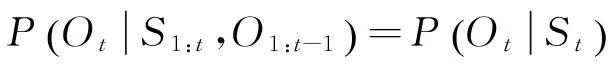
(2)

在已知观察序列的前提下，需要确定模型隐式状态数量、训练模型参数，并确定产生观察序列的最优状态序列。要完成上述任务，首先要解决2大问题，即模型参数训练问题和模型解码问题。参数训练问题是通过不断调整模型参数，使在已知模型下出现观察值概率最大化，Baum-Welch算法就解决了HMM的训练问题,即HMM参数估计问题。Baum-Welch算法可以得到模型参数，包括状态转移概率矩阵和生成观察值的概率矩阵。解码问题即如何有效地选取一组与观测值序列对应的状态序列，它能够对观测值序列作出充分的解释。解码问题可由Viterbi算法解决，该算法主要解决了在给定模型和观测值序列的条件下,在最优意义上确定状态序列的问题。

4 模型的建立

4.1 模型状态数量的确定

用HMM拟合降水序列时，需要先确定模型中隐式状态的数量，状态数量较少则无法充分反映降水特征，数量较多则会产生状态冗余，同时导致模型运行效率的下降[6]。应用较多的方法有赤池信息准则(AIC)(Akaike 1974)和贝叶斯信息准则(BIC)。两者都是基于最优似然函数值及相关参数来选择模型，BIC在计算中引入样本数量，较AIC的使用更有优势，因此，本文作者选择BIC确定模型中隐式状态数量[1,5,7]。其公式为

BIC=-2lgL+mlgn 。

(3)

式中：L表示模型似然函数的最大计算值；m表示参数的数量；n表示观察值的数量。

参照Hughes和Peter Guttorp在非齐次HMM中应用的模型状态数量确定方法，结合BIC最终确定本文模型中所需的状态个数为4。

4.2 模型参数训练

Baum等人(1970年)在综合考虑隐式状态的前提下提出了可以获得HMM参数最大化估计的方法，即Baum-Welch算法，也称为前向-后向算法。即在给定模型观察序列时用来解决模型参数训练问题，从一系列训练样本中通过多次迭代得到模型参数。

在HMM中，初始化时根据经验给模型的初始参数赋值，在遵循假设前提条件下通过不断迭代计算，使每一次修改得到的矩阵都更加可能产生观察序列，当前后2个2次迭代矩阵的变化在1个小的容错范围内时，迭代停止。最终参数收敛于最大似然估计值，并得到训练后的HMM参数(包括初始状态概率矩阵，状态转移矩阵A，观察值生成矩阵B)，使得该观察序列出现的可能性最大。根据以上基本原理并结合Matlab语言程序得到隐式状态的转移概率矩阵，见表2。

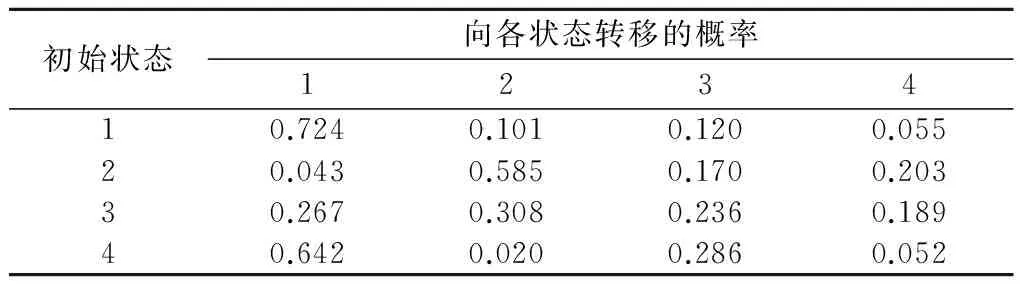
表2 HMM隐式状态转移概率

从表2可以得到HMM中所含各个隐式状态自身及相互之间转变的可能性。根据表中状态转移概率，状态1向自身转变的概率为0.724，占较大比重，说明其比较容易保持自身状态，向其余状态的转变概率(0.101,0.120,0.055)很小且相互之间差别不大，可知状态1不仅持续时间长，而且稳定性较高，可能对应着持续降雨或持续干燥的天气状态；状态2向自身转变的概率为0.585，也显示较高的自身稳定性，但与状态1相比，状态2也有着向状态3，状态4转变的较大可能；状态3的转移概率分布较为平均，向各个状态转变的可能性相差不大，说明该状态保持自身稳定性较低且转变影响因素较为复杂等；状态4与其余状态的转移情况相差较大，显示其向状态1转变概率最大(0.642)，还有较大可能向状态3转变。

根据Baum-Welch算法同时得到各状态下观察值生成概率矩阵，据此整理各城市降水概率，结果见图3。状态1中6个研究城市降水概率均在10%以内，显示降水可能性较低，整体显示天气干燥的状态；状态2与状态1呈现相反的情况，降水概率都在85%以上，有个别地区超过90%，降水概率极大，表明整体区域处于潮湿多雨的状态，其本质很可能是受夏季6—8月份大陆低压形成来自海洋的偏南暖湿气流影响导致雨水充沛；这2个状态可以分别表示全省干燥少雨和潮湿多雨的情况，且这类状态稳定性高，容易持续保持自身状态。状态3与状态4对6个研究城市降水概率的整体趋势影响相近，但状态3中各城市整体降水概率总体高于状态4下各城市降水概率，而且状态4中平均海拔最高的黄山市降水概率较其他城市明显差距更大，平均海拔最低的淮北市和毫州市却有相对最低的降水概率。结合省内地理特征，淮北地区(淮北市和毫州市)为辽阔的平原，海拔在20～40 m，地势低缓；江淮之间地区(合肥、滁州市和安庆市)多起伏的丘陵，大别山脉蜿蜒于该地区西南部；江南地区(黄山市)除沿江一部分为平原外，多数是山区地带，海拔在500～1 000 m，地势较高[8]，由于山高谷深，气候呈垂直变化，局部地形对其气候起主导作用，形成云雾多、湿度大、降水多的气候特点。因此我们可以推断状态4的特点主要是由地形特征(海拔、地势变化、地表起伏、地貌类型及结构、主要地形、典型地貌等几个方面)决定的。在状态4的推断下，状态3保留了地形特征的影响但其已被削弱，其降水概率特征显示很可能是海陆位置的影响占据了主要地位，同时受大区域整体气压带的控制，距离东部海洋位置相对较近的(合肥市、淮北市、黄山市、滁州市)降水概率相对较大，相对位置更加处于内陆(毫州市、安庆市)的则降水概率略低，由于前4个城市位置与后2个城市地理位置差距并不大，因此这6个城市降水概率整体平稳，并无异常值出现。

5 模型验证与分析

5.1 确定模型隐式状态序列

HMM中需要解决模型的一个基本问题，即解码问题：已知一个观察值序列和模型的各项参数，通过有效选取一组与观察值序列对应的状态序列，使它能够对观察值序列作出充分的解释。在本文的实际应用中，要得到决定天气晴雨状况的隐式状态序列，需要使用一种最优准则来解决此问题。目前最有效且应用较多的是Viterbi算法[2,8-9]，其详细过程如下。

定义在时刻t，沿着状态序列路径q1,q2,…qt,且qt=Si时产生的观察序列O1,O2,…，Ot的最大概率为P(i)，即

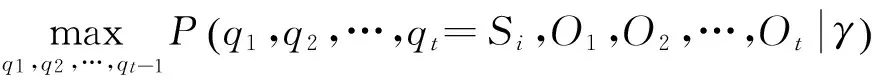
(4)

于是，求解最优状态序列q的过程如下。

(1) 初始化：

(5)

(2) 递归：

2≤t≤T,1≤j≤N ；

(6)

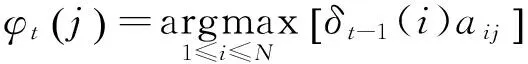
2≤t≤T,1≤j≤N 。

(7)

(3) 终止，最优概率：

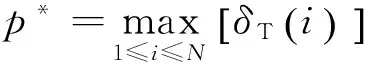
(8)

最终待定：

(9)

(4) 状态序列求解：

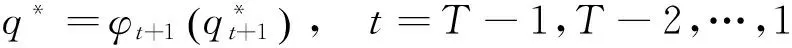
式中：aij为由状态i转移到状态j的概率；bij为状态i下生成观察值的概率。

由此得到最优状态序列q=q1,q2,…，qt。

通过Viterbi算法计算， 得到每个站点的最优隐式状态序列， 选取计算结果中合肥市1994年的隐式状态序列及各状态预测降水概率作简要说明， 见图3。 图3(a)部分(状态转移时间序列)显示隐式状态处于不断变化之中， 状态1倾向于保持自身状态， 同时有向状态2和状态4转变的可能， 而状态2除了延续自身状态， 也较容易向状态4转变， 状态4保持自身稳定性很低， 更容易向状态1转变； 图3(b)部分(各状态所占比例及同时间段内实际降水概率)显示状态1预测降水概率最大， 占67.3%， 状态2其次，占20.9%， 状态3和状态4预测降水概率较小， 状态2预测降水概率与真实观察值-降雨出现的频率接近。 上述情况补充说明了4.2节HMM参数训练中得到的状态转移相关结论， 再结合合肥市每年10月份的日状态序列数据整理(见图4)， 发现隐式状态分布规律并不明显，且存在较大年际间变化[6]。

图4 合肥市1994年的隐式状态变化趋势及各状态预测降水概率和实际降水概率

另外，对整体状态年变化做统计后发现：在前半时段内，状态1预测降水概率最高，占主导地位；状态2其次，在后半时段内状态1与状态2逐渐接近并且相互交替占主导地位，周期震荡趋势逐渐明显，表明安徽全省此时段内强降水频率及极端降水事件有略微上升的趋势，相互交替出现表明影响降水因素更为复杂多样，可能与人类相关活动更为密集有关[10-12]；状态3和状态4所占比例较低且稳定，表明地理位置、地势高低、大气循环等固定影响因素变化较为稳定，符合实际情况。各状态在1960—1999年的整体变化趋势见图5。

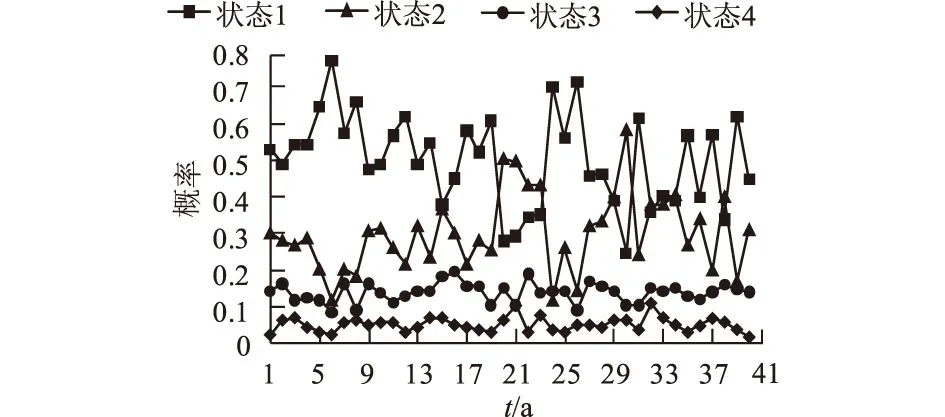
图5 1960—1999年各状态年变化概率趋势

5.2 模型验证

5.2.1 模拟期模型可行性

根据模拟期(1960—1999年)共40 a的实际年降水概率，与上述隐马尔可夫模型得出的年降水概率结果比较，发现模型结果符合实际情况，整体趋势匹配，而且两者之间拟合度较好，可见上述构造的隐马尔可夫模型具有较大可信性和可行性。模拟结果见图6。

图6 1960—1999年降水概率的HMM模拟值与实测值

5.2.2 验证期模型适用性

使用2000—2009年共10 a的降水数据，对上述构建的模型模拟未来10 a降雨概率进行适用性方面的分析。模拟结果如图7所示。结果表明本文构建的隐马尔可夫模型是适用于降水预测的，模拟准确度较高而且对异常值也有较好的预报结果。

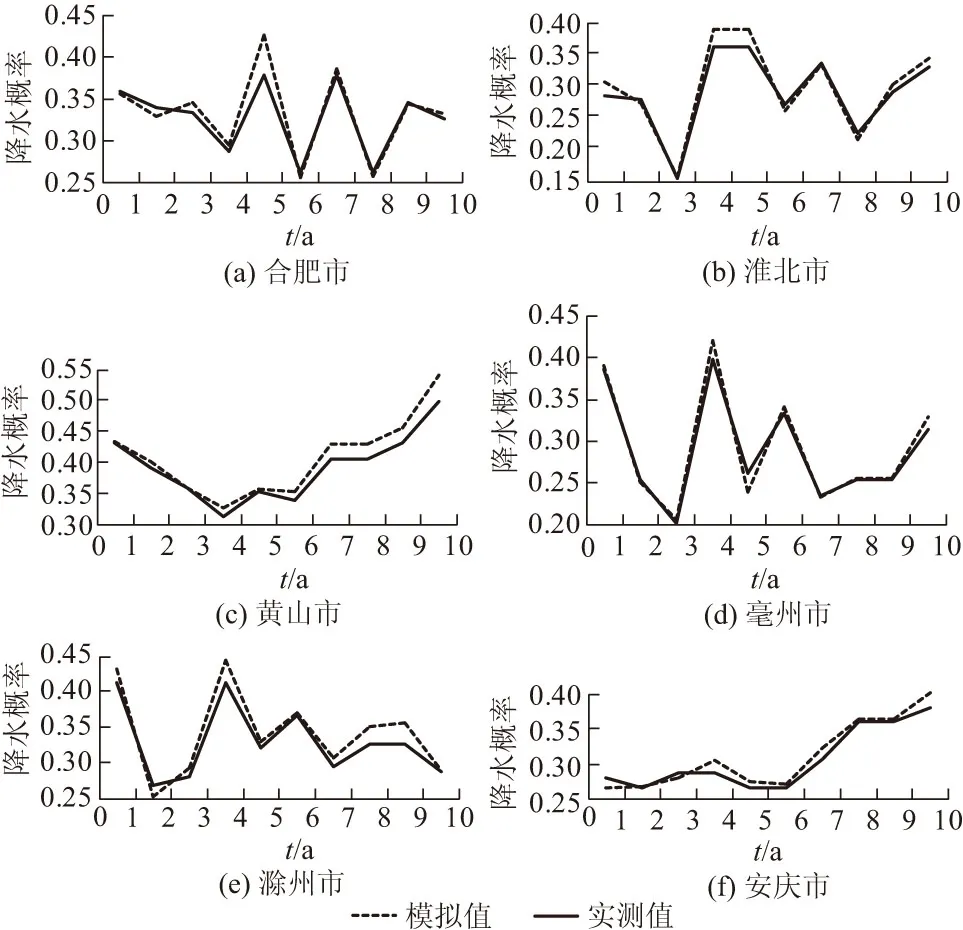
图7 2000—2009年降水概率的HMM模拟值与实测值

5.3 结果与讨论

根据上述模型的构建及分析、验证，我们得到了基于4个隐式状态的隐马尔可夫模型，对6个城市的降雨情况进行了模拟。状态1和状态2分别表示全省干燥少雨和湿润多雨的情况，状态3表示海陆位置及大区域气压带等因素，状态4表示各站点所处的地形特征、海拔等因素。隐马尔可夫模型中各隐式状态将大部分降雨的影响因素考虑在内，并不单独分析某一因素的影响，而是将其作为一个整体综合考虑，各状态在相互交替下影响区域降水情况[13-15]。模拟结果说明本文所构建的模型对研究区降水规律有较好的实用性。

在前期对马尔可夫模型的研究中， 本文作者曾选用灰色无偏马尔可夫模型对吉林省降水量进行预测， 该模型的平均相对误差值为0.051； 在本次研究中， 应用隐马尔可夫模型(HMM)进行降水概率预报， 其结果的平均相对误差为0.036。 此2种方法均以马尔可夫模型为基础进行改进， 以大量降水数据为样本开展计算， 同样对降水的状态变化进行预报， 二者具有可比性， 并且HMM产生的相对误差更小， 在数据拟合方面更具有优越性。

6 结 论

本文应用隐马尔可夫模型HMM对1960—2009年(共50 a)时段内安徽省6个水文气象站点的降水情况进行模拟，其中前40 a数据用来创建及训练模型，后10 a数据用来对模型进行验证。6个站点分别位于省内不同位置，模拟结果对全省降水预测具有代表性。根据贝叶斯信息准则BIC确定模型状态数量为4个。由于各站点的空间分布不均匀，因此4个状态对决定降水情况有不同的空间特征性。通过Baum-Welch算法对模型参数进行训练，使用Viterbi算法来根据可观察序列得到最优可能的隐藏状态的序列，对所建模型用模拟期和验证期2个序列对模型拟合，最终得到较好的模拟效果。同时与以前研究中通过无偏灰色马尔科夫模型对降水序列数据进行拟合的结果形成对比，结果表明HMM模拟的相对误差更小，更具适用性。

由于HMM是基于时间序列所创建的模拟过程，因此也可以应用于其他水文时间序列的相关研究，如地表径流、洪涝灾害、潮汐运动等方面。同时存在一些不足：例如在解决模型参数训练这个问题时使用最多的方法是Baum-Welch算法，但是Baum-Welch算法在解决这一问题时仍然存在缺陷，并不能一定保证求得全局最优模型，有时会得到一个局部最优结果，这就需要不断调整参数，并给模型赋予较为贴近真实结果的初始参数。因此，该模型还需要在以后的学习应用中进一步完善改进。

[1] HUGHES J P, GUTTORP P, CHARLES S P. A Non-homogeneous Hidden Markov Model for Precipitation Occurrence[J]. Applied Statistics, 1999, 48(1): 15-30.

[2] THYER M, KUCZERA G. Modeling Long-term Persistence in Hydro-climatic Time Series Using a Hidden State Markov Model[J]. Water Resources Research, 2000, 36(11): 3301-3310.

[3] THYER M, KUCZERA G. A Hidden Markov Model for Modelling Long-term Persistence in Multi-site Rainfall Time Series 1. Model Calibration Using a Bayesian Approach[J]. Journal of Hydrology, 2003, 275(1/2):12-26.

[4] HOLZMANN H, MUNK A, SUSTER M,etal. Hidden Markov Models for Circular and Linear-circular Time Series[J]. Environmental and Ecological Statistics, 2006, 13(3): 325-347.

[5] MARES C, MARES I, HUEBENER H,etal. A Hidden Markov Model Applied to the Daily Spring Precipitation over the Danube Basin[J]. Advances in Meteorology, 2014: 1-11. http://dx.doi.org/10.1155/2014/237247.

[6] 袁宏永, 张毛磊, 杨 锐，等.基于隐式Markov方法的福建省降水预测[J].清华大学学报(自然科学版),2010,50(6):887-890.

[7] BELLONE E, HUGHES J P, GUTTORP P. A Hidden Markov Model for Downscaling Synoptic Atmospheric Patterns to Precipitation Amounts[J]. Climate Research, 2000,15(1): 1-12.

[8] 陈 健,杜晓宾,方 茸，等. 安徽省夏季降水区域特征[J]. 气象科技,2012,40(5):794-798.

[9] 江俊杰,孙卫国.1959—2007年安徽省降水时空变化特征分析[J].中国农业气象，2012, 33(1):27-33.

[10]BETRO B, BODINI A, COSSU Q A. Using a Hidden Markov Model to Analyse Extreme Rainfall Events in Central-East Sardinia[J]. Environmetrics, 2008, 19(7): 702-713.

[11]KEHAGIAS A. A Hidden Markov Model Segmentation Procedure for Hydrological and Environmental Time Series[J]. Stochastic Environmental Research and Risk Assessment, 2004, 18: 117-130.

[12]RAMESH N I, ONOF C. A Class of Hidden Markov Models for Regional Average Rainfall[J]. Hydrological Sciences Journal,2014, 59(9): 23-38.

[13]SANSOM J. Hidden Markov Model for Rainfall Using Breakpoint Data[J]. Journal of Climate, 1997, 11(1): 42-53.

[14]LEROUX B G. Maximum-likelihood Estimation for Hidden Markov Models[J]. Stochastic Processes and Their Applications, 1992, 40(1): 127-143.

[15]张 茜,梁秀娟,杜 川. 基于无偏灰色马尔可夫链的吉林省降水量预测[J]. 吉林大学学报(地球科学版),2014,(6):1973-1979.

(编辑：刘运飞)

Research of Precipitation Characteristics in AnhuiProvince Using Hidden Markov Model

HUO Feng-lan1, ZHANG Qian2, A Ru-na3, LIU Xiao-mei4, BAO Shu-ming5, WU Yun-fei5, BAO Shi-chao5, LI Shu-sen5

(1.Supplies Management Station for Flood Control and Drought Relief of Tongliao City,Tongliao 028000,China；2.College of Environment and Resources, Jilin University, Changchun 130021, China； 3.Inner Mongolia Electric Power Science Research Institute, Hohhot 010020, China； 4.Quality and Safety Surveillance Station for Water Conservancy Project Construction in Tongliao City, Tongliao 028000, China；5.Water Conservancy Planning Design and Research Institute of Tongliao City, Tongliao 028000, China)

The laws and characteristics of precipitation in Anhui Province were analyzed and simulated using the Hidden Markov Model (HMM) to verify its applicability in regional precipitation. HMM with four implicit states was employed to fit the daily precipitation data sequence of many years in six major cities in the province. Bayesian Information Criterion was adopted to determine the implicit state quantity, the Baum-Welch algorithm to train and obtain the optimal model parameters, and the Viterbi algorithm to determine the optimal sequence of the model states. The above methods were adopted to simulate the precipitation in the summer of 1960-2009 in six cities of Anhui Province. The first 4-decade was for model training and analyzing, and the later 1 decade for model validation and evaluation. Results showed that HMM is of high practicability by better simulating rainfall characteristics.

hidden Markov model; implicit state; precipitation characteristics; Bayesian information criterion; Baum-Welch algorithm; Viterbi algorithm

2016-04-26；

2016-07-19

国家自然科学基金项目(41072171)

霍凤岚(1963-)，女，内蒙古通辽人，高级工程师，主要从事水利工程建设管理，(电话)18747339991(电子信箱)tlsl401@sohu.com。

张 茜(1989-)，女，黑龙江哈尔滨人，博士研究生，主要从事水文学与水资源方面的研究，(电话)15124510766(电子信箱)qianer0403@126.com。

10.11988/ckyyb.20160406

2017,34(1):12-18

P401

A

1001-5485(2017)01-0012-07